轴线倾斜对推力锥润滑特性的影响及修形参数优化研究*
魏 峥 李 硕 裴世源 洪 军
(1.西安交通大学现代设计与转子轴承系统教育部重点实验室 陕西西安 710000;2.中国船舶重工集团公司第七〇三研究所 黑龙江哈尔滨 150036)
在船舶齿轮变速箱中,为了提高变速箱的传递效率和降低成本,常采用斜齿轮传动搭配推力锥结构替代人字齿轮传动。如图1所示,与传统船舶齿轮箱相比(见图1(a)),采用推力锥结构(见图1(b))能够平衡斜齿轮啮合过程中产生的轴向力,从而有效地消除斜齿轮转子的倾覆力矩。其工作原理为:在小齿轮的两侧安装推力锥并在其对应的大齿轮轮缘端面设有相密合的锥面,推力锥的锥形面和与斜齿轮侧面磨合的接触面导致重叠区域的间隙变窄从而形成收敛的楔形空间;由于锥角的存在,2个锥面之间在旋转过程中相对滑动,在润滑油的作用下可形成流体动压润滑膜;小齿轮啮合过程中产生的轴向力通过推力锥、润滑油膜传递到大齿轮锥面,并与大齿轮啮合过程中产生的轴向力大小相等、方向相反,实现了轴向力的平衡[1-2]。
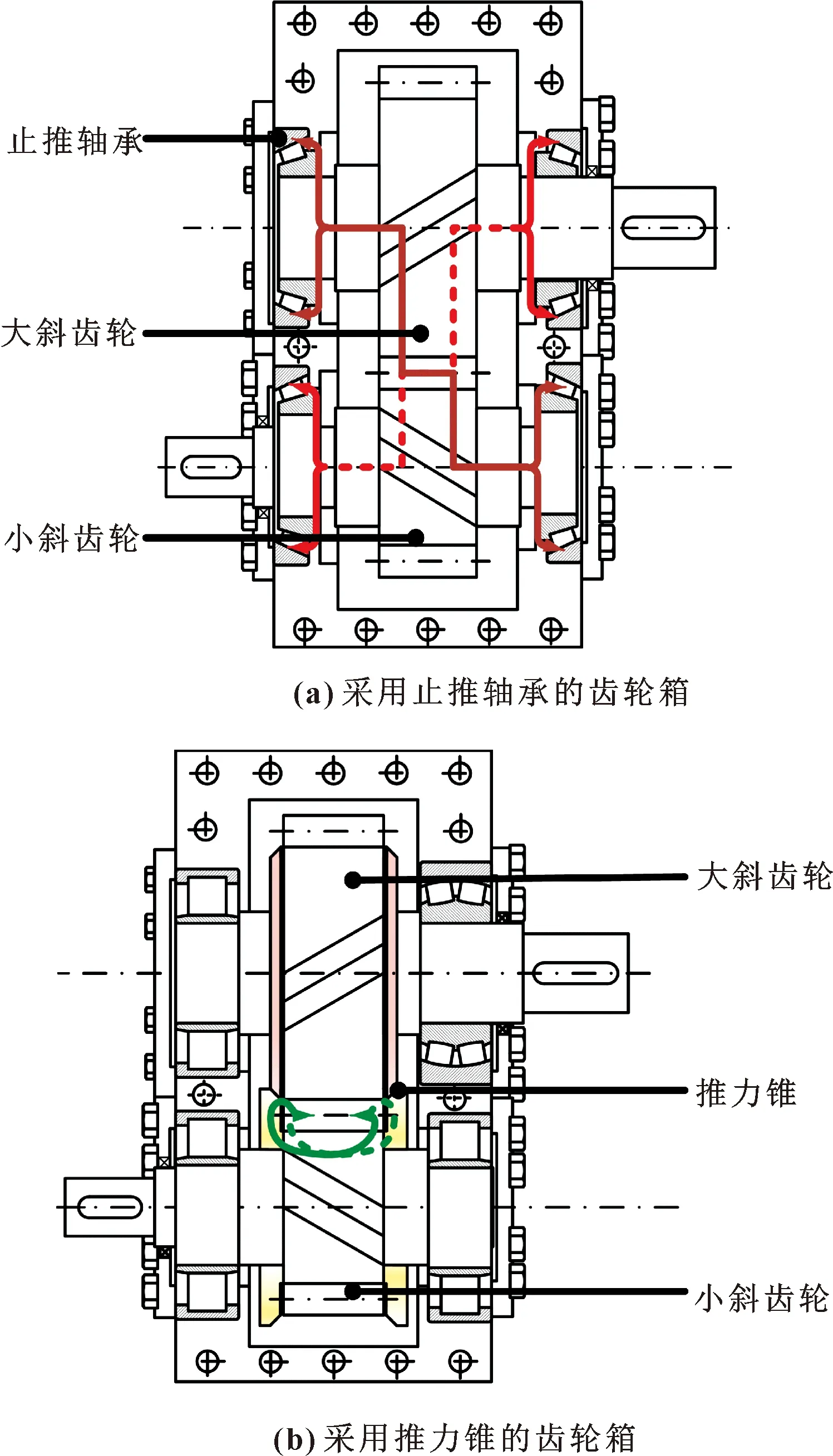
图1 船舶齿轮箱结构
自20世纪80年代以来,学者们对推力锥的润滑性能开展了深入的研究。LANGER[3]首次使用有限元法计算出等温弹流润滑条件下推力锥的数值解。SIMON[4]考虑热效应,用有限差分法求解出推力锥的热弹流数值解。文献[5-7]从理论上分析了理想圆锥推力锥液膜的形成,在对推力锥结构的弹性流体力学分析中考虑了轮缘接触处的弹性变形和压力黏性效应,并设计了一种液膜厚度测量装置对计算结果进行验证。刘福林[8]推导出高速齿轮箱中推力锥接触间隙的精确计算公式,分析了推力锥表面速度和相对滑动速度沿接触母线方向的变化情况,在考虑速度变化的同时用推导出的公式计算出推力锥等温弹流润滑的数值解。
综上所述,虽然学者们对推力锥的润滑特性进行了较充分的研究,这些研究成果为深入研究推力锥的润滑性能提供了理论基础。但在推力锥的实际应用中,由于制造和装配等造成的推力锥转子轴线倾斜,会导致推力锥的边缘膜厚减小,油膜压力和油膜温升急剧增大,使得推力锥的润滑性能严重恶化。针对此问题,本文作者建立了考虑轴线倾斜和锥面局部修形的推力锥点接触热弹流润滑模型,对比研究了典型工况下转子轴线斜率对推力锥修形前后润滑性能的影响,并分析了修形参数对锥面局部修形推力锥润滑性能的影响,得到了修形参数的最优取值范围。
1 理论基础
1.1 控制方程
稳态、不可压缩条件下,忽略密度沿z方向变化,推力锥的二维弹流Reynolds方程可描述为如下形式:
(1)
式中:x为周向坐标;y为轴向坐标;η为润滑油黏度;us为推力锥周向平均速度;p为油膜压力;h为油膜厚度。
润滑油的密度方程[9]为
(2)
式中:ρ0为润滑油的初始密度;p为油膜压力;T为油膜温度;T0为润滑油初始温度;D为密度-温度系数,文中取其值为-3.5×10-4℃-1。
润滑油的黏度方程使用Roelands黏压-黏温关系式表示,其表达式为
(3)
式中:η0为润滑油的初始黏度;p0为压力黏度系数,文中取值为1.96×108;z1为黏压指数,文中取值为0.68;S0为黏温系数,文中取值为-1.1。
推力锥的弹性变形可通过Boussinesq积分式计算得到:
(4)

载荷方程为
(5)
式中:w为推力锥的外载荷。
推力锥周向平均速度方程[8]为
(6)
式中:n1、n2分别为大斜齿轮和推力锥的转速。
不考虑热辐射的影响,润滑剂的导热系数和等压比热容作为常数处理,由于密度变化而产生的压力功对计算结果影响较小故将其忽略,则能量方程[10]可写为
(7)
式中:cp为润滑油的等压比热容;u、v分别为润滑油的周向和轴向的速度;λ为润滑油的导热系数。
膜厚方向的速度场方程为
(8)
式中:h为节点的油膜厚度;z为节点的膜厚坐标。
推力锥与大斜齿轮的接触界面方程为
(9)
式中:ρ1、ρ2分别为大斜齿轮和推力锥的密度;λ1和λ2分别为其导热系数;c1和c2分别为其比热容。
(1)普通推力锥膜厚公式
图2(a)展示了推力锥间隙(推力锥锥面和大斜齿轮锥面由于锥面形状而产生的间隙)的形状。建立如图2(b)所示坐标系,间隙计算公式推导如下(具体推导见参考文献[8])。

图2 推力锥工作简图
(10)
其中:
式中:d1、d2分别为大斜齿轮和推力锥的外圆直径;r1,r2分别为其接触母线中点半径;β为推力锥的锥角,β=90°-θ。
如图3所示,当推力锥的转子轴线倾斜时,推力锥的锥面随之倾斜,锥面间隙d(x,y)相应地要加上轴线倾斜导致的间隙变化,文中假设转子轴线为一条斜率为kl的直线,故推力锥的膜厚方程的表达式为
h(x,y)=h0+d(x,y)+v(x,y)-kly
(11)
式中:h0为推力锥中心膜厚;kl为推力锥转子轴线斜率,kl=tanγ,γ为轴线倾斜的角度(轴线顺时针倾斜为正,逆时针倾斜为负)。
(2)修形推力锥膜厚公式
如图4所示,对推力锥两端修圆(文中修形只考虑两端修圆),分别在推力锥的两侧修圆,两侧的修形深度和修形宽度相同,其修形表达式如下式所示:
(12)
式中:Mh为两端修圆推力锥的修形深度;Mw为修形宽度;ys和ye分别为推力锥两侧修形的起点位置坐标。
两端修圆推力锥膜厚方程的表达式为
h(x,y)=h0+d(x,y)+v(x,y)-kly+hm
(13)
两端修圆推力锥除膜厚方程外其余控制方程与不修形推力锥的控制方程相同。
推力锥弹流润滑计算模型与椭圆接触弹流润滑计算模型相比有以下两点不同之处:
(1)由式(6)可知,推力锥与大斜齿轮2个锥面之间存在速度差,锥面的平均速度us不是一个定值,以文中建立的坐标轴为例,平均速度随着y坐标的增大而增大,因此,油膜压力更集中分布在接触区域左半部分(y轴负方向),推力锥的压力分布也无法像椭圆接触一样对称分布。
(2)推力锥与椭圆接触的膜厚方程不一样,推力锥的膜厚方程需要使用考虑推力锥实际形状的间隙方程。
1.2 边界条件和润滑特性计算
(1)边界条件
Reynolds的压力边界条件如下式所示:
(14)
式中:xin、xout分别为求解域入口边界和出口边界的x向坐标;yin为求解域入口边界的y向坐标。
能量方程的温度边界如下式所示:
(15)
(2)润滑特性计算
文中推力锥流量用推力锥最小油膜厚度所在截面的进油量来表示,其表达式如下式[11]所示:
(16)
式中:h1为推力锥的最小油膜厚度;Q为推力锥流量。
将计算迭代收敛后的润滑油膜厚度加减一个极小的厚度s(s一般小于1 μm),按照求解Reynolds方程的有限差分格式求解油膜厚度变化后的压力,两者之间差值的绝对值记作ΔF,则推力锥的刚度计算公式为
(17)
1.3 求解方法
为了提高计算效率与计算的准确性,文中将推力锥润滑计算区域划分为206×56的正方形网格,其中x方向的网格数Nx为206,y方向的网格数Ny为56。在z方向将各节点膜厚均匀地划分网格,其网格数Nz为5。
推力锥的热弹流计算流程框图如图5所示,具体计算步骤如下:

图5 推力锥弹流润滑计算流程
(1)输入推力锥已知的工况参数(润滑油参数、转速和载荷等)和几何参数(接触母线长度、推力锥半径和锥角等)。
(2)采用HAMROCK和DOWSON[12]的方法计算式(4),得到推力锥的弹性变形矩阵,在后续计算膜厚时直接调用弹性变形矩阵来提高计算效率。
(3)给定推力锥的初始中心膜厚h0、初始压力分布p和初始温度分布T。
(4)根据给定的压力分布和温度分布按式(2)—(5)计算推力锥接触区域的密度分布、黏度分布和膜厚分布。
(5)将得到的密度分布、黏度分布、膜厚分布和压力分布代入Reynolds方程,使用有限差分法[13]求解得到新的压力分布,取压力松弛因子为0.15计算更新后的压力p,将求解前的压力用pold表示,压力迭代的收敛准则如下:
(18)
若计算结果未达到收敛条件,将迭代后的压力回代,重新计算润滑油的密度分布、黏度分布和推力锥的膜厚分布,直至达到压力收敛条件。
(6)压力达到收敛条件后,使用下式判断载荷是否收敛:
(19)
式中:ζw为推力锥的载荷收敛精度,常取值为0.01~0.001,文中取值为0.005。
若计算结果未达到载荷收敛条件,取载荷松弛迭代因子为0.005更新中心膜厚h0重新计算,直至达到载荷收敛条件。
(7)根据能量方程(9)、接触界面方程(10)和温度边界条件,使用追赶法求解得到温度场,为保证计算收敛对入口温度使用逆流迭代法[14]计算,取收敛因子为0.31计算更新后的温度T,将求解前的温度用Told表示,温度收敛准则如下:
(20)
若计算结果未达到收敛条件,则将得到的温度T回代,重新计算压力和膜厚直至达到温度收敛条件。
1.4 计算验证
图6所示为推力锥实际接触区域。由图6和图2可知,推力锥的实际接触区域类似一个椭圆区域,但在实际计算过程中,为了提高计算的速率,可将其区域简化为一个矩形计算,且简化后对计算结果的影响不大。为了验证文中计算方法的正确性,选取文献[15]和文献[5]中的算例分别对比推力锥在热弹流和等温弹流条件下的计算结果。
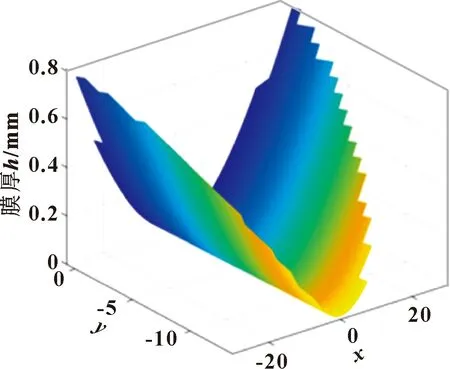
图6 推力锥实际接触区域
1.4.1 等温弹流计算验证
参考文献[5]中算例的几何参数和工况参数如表1所示。

表1 等温弹流算例参数[5]
按图5所示的流程框图进行求解,得到了推力锥的压力分布和膜厚分布。图7(a)所示是过推力锥接触母线中点(y=-Δ)截面的x向压力分布和膜厚分布,图7(b)所示是过x=0截面的y向压力分布和膜厚分布。可以看到,文中求解得到的油膜压力和油膜厚度总体分布均略大于文献[5]结果,在该工况条件下,文献[5]计算得到的最小油膜厚度为1.34 μm,文中结果为1.12 μm,误差小于20%。
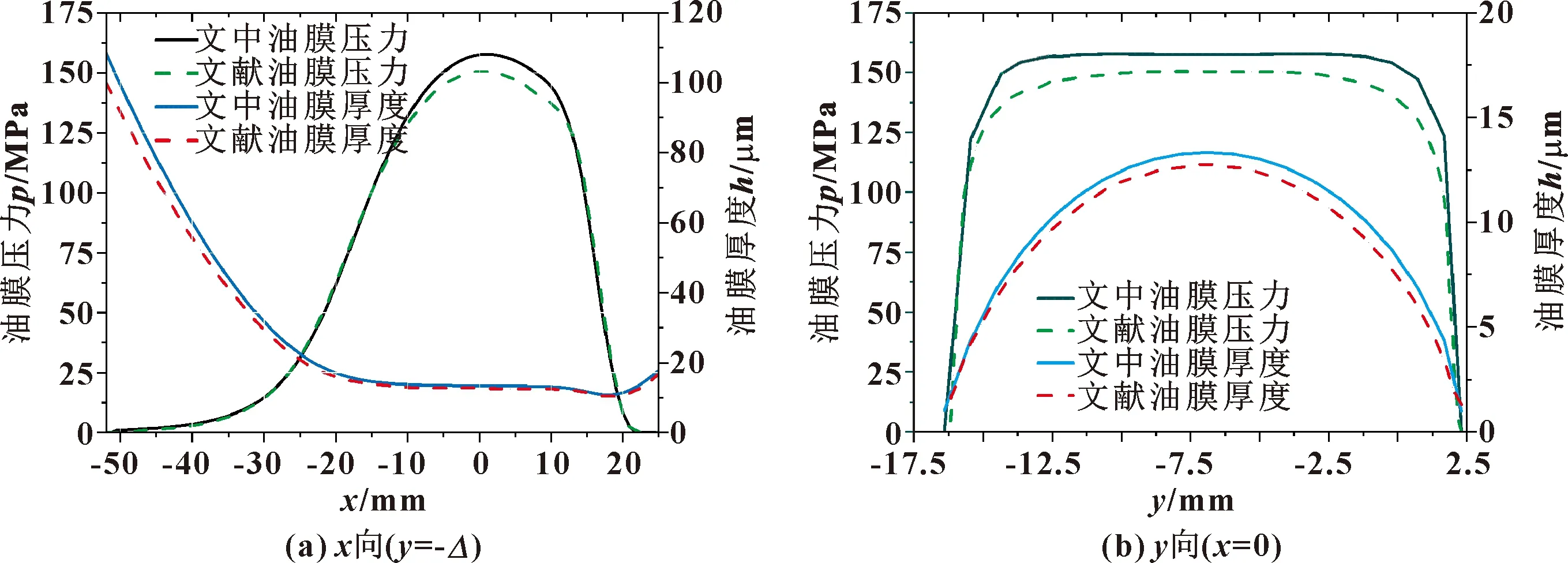
图7 文献[5]和文中膜厚、膜压对比
1.4.2 热弹流润滑计算验证
参考文献[15]中算例的几何参数和工况参数如表2所示。

表2 热弹流算例参数[15]
采用上文所述的计算方法按图5所示流程图计算出表3中工况条件下的最小膜厚为8.441 μm,与文献[15]计算结果8.437 μm相差0.004 μm左右。

表3 推力锥的几何和工况参数
综上所述,文中计算结果与文献[15]、[5]计算结果相差较小,验证了文中计算方法的正确性。
2 结果与讨论
文中通过对推力锥两端修圆的修形方式来改善转子轴线倾斜条件下推力锥的润滑性能,计算相同工况条件下推力锥修形前后的润滑性能并进行对比,验证修形改善推力锥润滑性能的合理性。推力锥的几何和工况参数见表3。
2.1 典型工况下压力、膜厚和温升分布
图8—10分别展示了推力锥的油膜压力、油膜厚度和油膜温升的分布情况。与普通椭圆接触热弹流润滑的计算结果相比,典型工况下推力锥的压力分布没有二次压力尖峰,油膜也未出现颈缩现象,这主要是因为推力锥的转速较高。当推力锥的转速较小时,推力锥的油膜厚度也会出现颈缩现象,如图7所示。
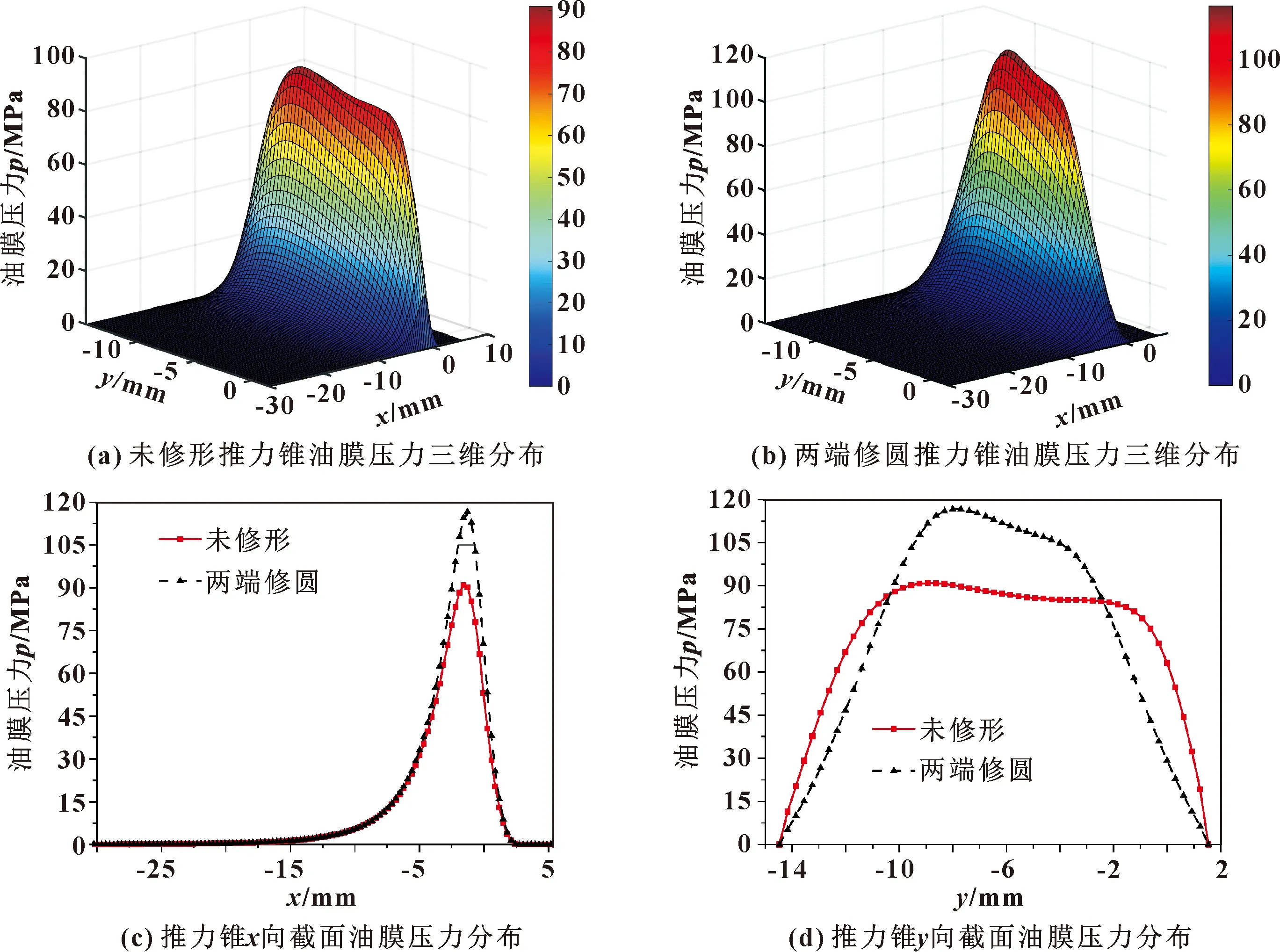
图8 推力锥修形前后油膜压力分布
由图8可见,修形前后推力锥的油膜压力峰值所在位置基本相同,两端修圆推力锥的油膜压力峰值约为120 MPa,未修形的油膜压力峰值约为90 MPa;修形后推力锥的油膜压力更集中分布在接触区域未修形的位置,这是因为修形后推力锥的承载区域减小。
由图9可见,修形前后推力锥的油膜厚度在x向的分布变化较小,修形后推力锥的最小油膜厚度相较于修形前有所提高;由于修形前后推力锥在接触区域y向边界的形状有较大的差距,修形后推力锥的油膜厚度在y向边界处远大于修形前。

图9 推力锥修形前后油膜厚度分布
由图10可见,两端修圆推力锥的最高油膜温升约为40 ℃,未修形推力锥最高油膜温升约为33 ℃。推力锥的油膜温升和油膜压力的y向分布趋势基本一致,推力锥两端修圆后,未修形区域压力增大,润滑油黏度增大,油膜剪切力增大,油膜温升上升。

图10 推力锥修形前后油膜温升分布
2.2 典型工况下润滑性能对比
求解出推力锥修形前后的油膜厚度分布、油膜压力分布和油膜温升分布后,根据式(16)(17)计算推力锥修形前后的关键润滑性能参数,计算结果如表4所示。

表4 典型工况下推力锥修形前后润滑特性
由表4可知:相同工况条件下,推力锥两端修圆后最小油膜厚度约增大了20%,最大油膜压力增大了约30 MPa,修形后推力锥的流量和刚度也有所增大,最大油膜温升仅增加了8 ℃左右。因此,可以判断当推力锥转子轴线倾斜时,对推力锥进行两端修圆可以有效地改善推力锥的润滑性能。
不同零部件的弹流油膜范围是不同的,滚动轴承的弹流膜厚范围为0.1~1 μm,滑动轴承弹流膜厚范围为5~50 μm。推力锥是一种新结构,其弹流油膜范围受轴向载荷的影响,轴向载荷较大(>80 kN)时推力锥的弹流膜厚在1 μm左右,一般工况下,推力锥承受的轴向载荷较小,推力锥弹流膜厚范围为5~20 μm。由表4可知,典型工况下未修形推力锥的最大弹性变形为5.71 μm,达到了最小膜厚的70%以上,两端修圆推力锥的最大弹性变形为6.43 μm,达到最小膜厚的65%以上。如果不考虑弹性变形直接计算,推力锥的最大油膜压力也会由90.93 MPa增大至108.36 MPa(增大20%左右),因此,推力锥必须考虑弹性变形的影响。
2.3 转子轴线倾斜对润滑性能的影响
通过分析不同转子轴线斜率下推力锥修形前后的润滑性能,进而研究转子斜率对推力锥润滑性能的影响。图11对比了推力锥修形前后的最大油膜压力随转子轴线斜率的变化。图12对比了推力锥修形前后的最小油膜厚度随转子轴线斜率的变化。图13给出了斜率为0和3×10-4条件下不修形推力锥的y向压力分布和膜厚分布。图14对比了推力锥修形前后的最大油膜温升随转子轴线斜率的变化。图15对比了推力锥修形前后流量随转子轴线斜率的变化。

图11 转子轴线斜率对最大油膜压力的影响

图12 转子轴线斜率对最小油膜厚度的影响

图13 不同斜率下推力锥y向膜厚、压力分布
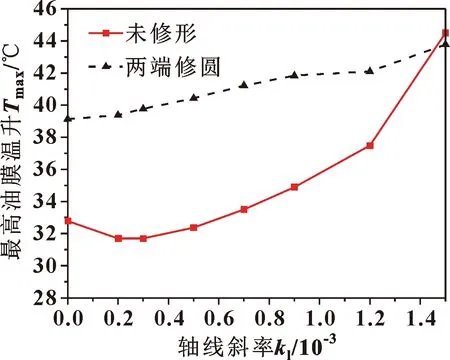
图14 转子轴线斜率对最高油膜温升的影响

图15 转子轴线斜率对流量的影响
由图11可见,随着转子轴线斜率的增大,推力锥的最大油膜压力先减小后逐渐增大。由图13(b)和式(13)可知,当转子轴线不倾斜时,油膜压力集中分布在推力锥接触区域的左半部分,随着转子斜率的增大,y>0区域的油膜厚度逐渐减小,油膜压力逐渐集中分布在推力锥接触区域的右半部分,最大油膜压力出现的位置逐渐向y轴正方向移动,因此,推力锥的最大油膜压力先减小后增大。
由图12可见,随着转子轴线斜率的增大,推力锥的最小油膜厚度平缓减小。转子轴线斜率在0~1.5×10-3的范围内,两端修圆推力锥的最小油膜厚度始终大于未修形推力锥的最小油膜厚度且两者差值随着转子轴线斜率的增大而增大。
为了研究推力锥最大油膜压力下降,最小油膜厚度仍减小的原因,图13中比较了斜率为0和3×10-4条件下不修形推力锥的y向压力分布和膜厚分布,并标出了最大油膜压力和最小油膜厚度的位置坐标。可以看到,随着转子轴线斜率的增大,推力锥油膜压力更加集中分布在接触区域的右半部分,最大油膜压力位置逐渐向y轴正方向移动,推力锥润滑油出口处附近的油膜压力不断增大,而最小油膜厚度的位置也在润滑油出口处。因此,推力锥的膜厚随着转子轴线斜率的增大不断减小。
由图14可见,随着转子轴线斜率的增大,推力锥的最高油膜温升先减小后增大,其变化趋势与最大油膜压力变化趋势基本一致,最大油膜压力减小,润滑油黏度减小,剪切力减小,最高油膜温升增大。当转子轴线斜率大于9×10-4时,未修形推力锥最大油膜压力迅速增大,因此,最高油膜温升随之迅速上升。
由图15可知,随着转子轴线斜率的增大,推力锥的流量平缓减小。由于文中计算的流量是通过推力锥最小膜厚所在截面的流量,因此,两者的变化趋势也相同。
由图11—15可知,在转子轴线倾斜的条件下,两端修圆修形对推力锥润滑性能的优化主要体现在最小油膜厚度的增大,且转子轴线斜率越大修形后推力锥最小油膜厚度增加得越大。当转子轴线斜率较大(>1.2×10-3)时,推力锥两端修圆后的最小油膜厚度几乎增加了1.5倍。
2.4 最佳修形参数分析
修形宽度占比(两端修圆推力锥一侧的修形宽度Mw占接触长度YL的比例)和修形深度是两端修圆推力锥的关键修形参数,为了得到最佳的修形参数范围以便后续设计两端修圆推力锥,文中对两端修圆推力锥进行修形参数化分析。
2.4.1 修形宽度占比
图16所示为典型工况条件下(如表3所示),修形宽度占比为0.05~0.5时,修形宽度对两端修圆推力锥润滑特性的影响。

图16 修形宽度占比对最大膜压和最小膜厚的影响
由图16可知,随着修形宽度占比的增大,推力锥主要承载区域减小,压力集中分布在接触区域中心处,两端修圆推力锥的最大油膜压力平缓增大。推力锥的最小油膜厚度随着修形宽度占比的增大平缓增大,出现了最小膜厚和最大膜压同时增大的现象。
为研究最小膜厚和最大膜压同时增大的原因,图17对比了两端修圆推力锥在不同修形宽度下的y向压力分布和膜厚分布。可见,修形宽度占比为0.35的两端修圆推力锥的油膜压力大于修形宽度占比为0.20的推力锥时,前者的油膜厚度明显小于后者,但由于转子轴线倾斜,两者的最小油膜厚度均出现在推力锥修形的右起始点附近且前者的最小油膜厚度位置在后者的左侧,所以出现了最大油膜压力增大,而最小油膜厚度也增大的现象。
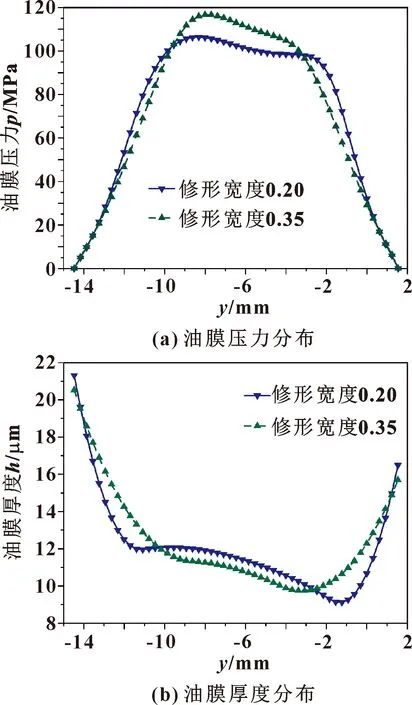
图17 不同修形宽度占比下推力锥y向膜压、膜厚分布
图18所示为修形宽度占比对流量和最高油膜温升的影响。可知,随着修形宽度占比的增大,两端修圆推力锥的最高油膜温升平缓增大,温升的总体变化不超过7 ℃,可见修形宽度占比对最高油膜温升的影响相对较小。两端修圆推力锥的流量随着修形宽度占比的增大平缓增大,其变化趋势与最小膜厚的变化趋势一致。
由图16—18可知,修形宽度占比对两端修圆推力锥的最大油膜压力和最小油膜厚度影响较大,对刚度和最大油膜温升影响较小。当修形宽度占比小于0.2时,推力锥的最小油膜厚度增长较快。当修形宽度占比的范围为0.2~0.35时,推力锥的最小油膜厚度平缓增长,该范围内推力锥的最小油膜厚度已经度过了快速增长的阶段,最高油膜温升与40 ℃有一定的安全裕度且修形加工范围相对较小。因此推力锥修形宽度占比的最优范围为0.2~0.35。
2.4.2 修形深度
图19所示为典型工况条件下(如表3所示),修形深度为0~20 μm时,修形深度对两端修圆推力锥润滑特性的影响。
由图19可知,随着修形深度的增大,两端修圆推力锥两端的油膜厚度迅速增大,两端的油膜压力减小,压力集中分布在未修形处,因此,推力锥的最大油膜压力几乎线性增大。两端修圆推力锥的最小油膜厚度随着修形深度的增大先迅速增大后平缓减小,当修形深度小于4 μm,最小油膜厚度增长幅度较大。
图20对比了两端修圆推力锥不同修形深度下油膜压力和油膜厚度的y向分布。可知,当修形深度较小时,在轴线倾斜的条件下,推力锥右侧由于修形而增加的膜厚小于轴线倾斜减小的膜厚,此时最小油膜厚度出现在润滑区域出口处;随着修形深度的增大,推力锥的最小油膜厚度所在位置逐渐左移至推力锥修形的起始点位置;推力锥最小油膜厚度逐渐增大;随着修形深度继续增大,推力油膜压力更集中分布在未修形区域,修形起始点处油膜压力增大,因此,油膜厚度开始逐渐减小。
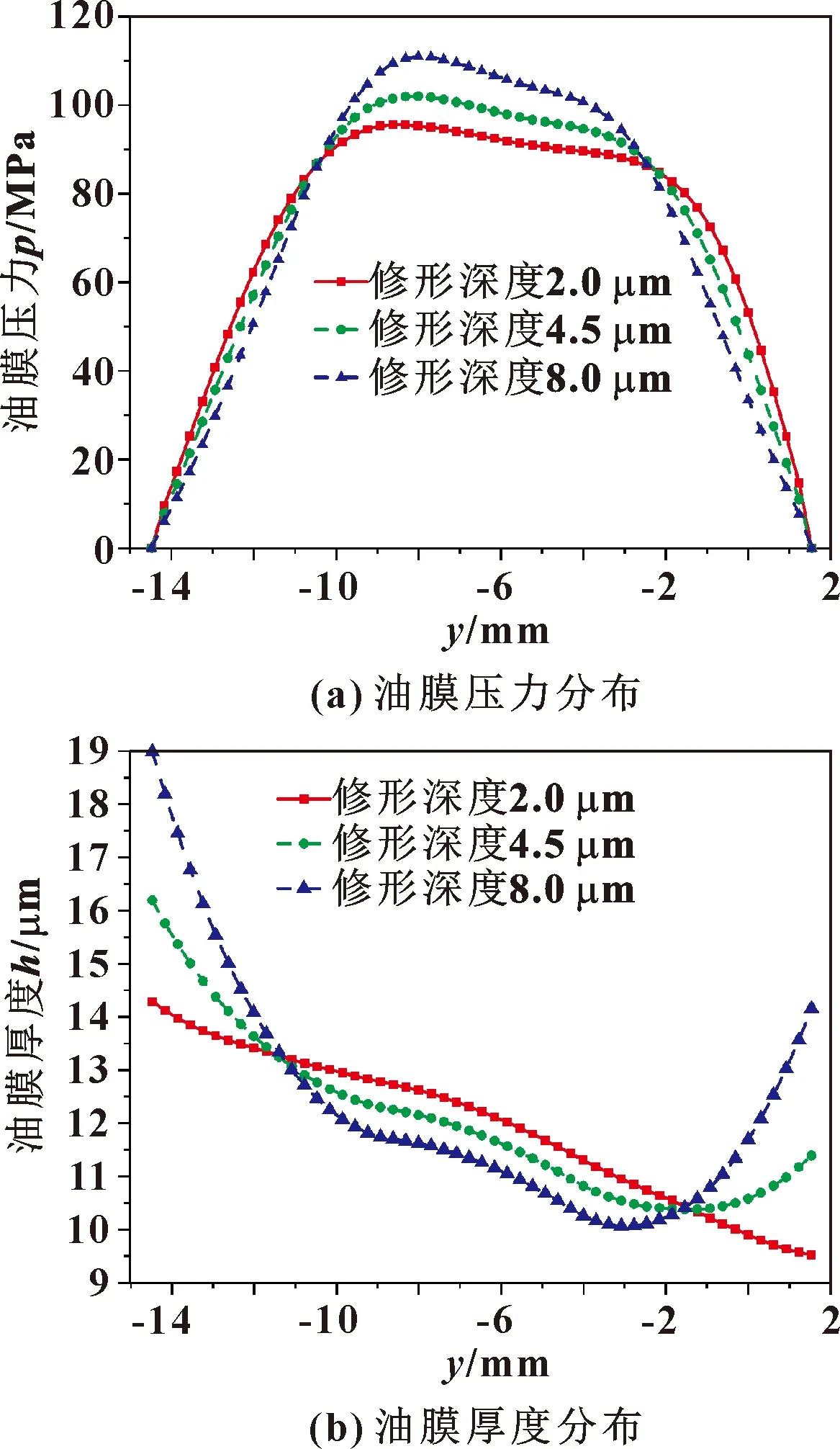
图20 不同修形深度下推力锥y向膜压、膜厚分布
图21所示为修形深度对最高油膜温升和流量的影响。可知,随着修形深度的增大,两端修圆推力锥的最高油膜温升几乎线性增大,与最大油膜压力变化趋势一致,修形深度对最高油膜温升的影响较大;两端修圆推力锥流量的变化趋势与最小膜厚的变化趋势一致。
由图19—21可知,修形深度对推力锥的油膜厚度影响较大,存在最优修形深度使得推力锥的油膜厚度最大。当修形深度小于2 μm时,推力锥的最小油膜厚度增长较快;当推力锥的修形深度为2~8 μm时,该范围内推力锥的最小油膜厚度较大且可以取到最优修形深度,最高油膜温升与40 ℃有一定的安全裕度。因此两端修圆推力锥修形深度的最优取值范围为2~8 μm。
3 结论
建立了转子轴线倾斜条件下推力锥修形前后的点接触热弹流润滑润滑数学模型并通过算例计算验证了数学模型的正确性,计算对比了典型工况条件下推力锥修形前后的润滑性能,研究了转子轴线斜率对推力锥的润滑性能的影响,分析了修形参数对两端修圆推力锥润滑性能的影响。主要结论如下:
(1)典型工况条件下,推力锥两端修圆后除油膜温升增加了7 ℃外,其余润滑性能均得到了优化。
(2)转子轴线斜率是影响推力锥润滑性能的重要因素,转子轴线斜率增加,推力锥的最小油膜厚度和流量快速减小;最大油膜压力先减小后增大。
(3)与不修形推力锥相比,两端修圆推力锥在转子轴线倾斜的条件下能够有效地增大推力锥的最小油膜厚度、流量等关键润滑性能参数。当转子轴线斜率较小(<1.2×10-3)时,推力锥两端修圆后除最高油膜温升略有增加外,其余润滑性能均得到了优化。
(4)转子轴线斜率较大(>1.2×10-3)的条件下,推力锥两端修圆后的最小油膜厚度增大为原来的2.5倍,除最高油膜温升略有增加、最小油膜压力略有下降外,其余润滑性能均得到了优化。因此,两端修圆推力锥在转子轴线倾斜的条件下能够保证推力锥的正常工作。
(5)修形深度和修形宽度占比是影响两端修圆推力锥最小油膜厚度的关键因素,修形宽度占比的最优取值范围为0.2~0.35,修形深度的最优取值范围是2~8 μm。

