考虑界面滑移和惯性力效应的水润滑轴承润滑性能分析*
解忠良 田佳彬 杨 铭 王五成 陈汝刚 杨 康 刘 琦 秦卫阳
(1.西北工业大学工程力学系 陕西西安 710072;2.武汉第二船舶设计研究所 湖北武汉 430205;3.中国船舶及海洋工程设计研究院 上海 200011;4.中国人民解放军海军装备部驻沈阳地区军 事代表局驻大连地区第一军事代表室 辽宁沈阳 210100;5.中国舰船研究设计中心 湖北武汉 430064;6.西安电子科技大学机电工程学院 陕西西安 710071)
水润滑轴承以水为润滑和工作介质,具有无污染、来源广泛、安全性和难燃性等优点,能降低和减少因摩擦副的运动而产生的磨损、噪声、功耗等问题,使其在环保、节能、可持续发展等方面有巨大潜力。目前针对水润滑轴承润滑机制、润滑性能等方面的研究尚显不足,综合考虑界面滑移和惯性力效应对水润滑轴承润滑机制和润滑性能影响的研究文献更少。
流体流动的边界条件是决定流体动力学行为的重要因素之一。一直以来,经典流体力学、润滑理论以及科技论文中,都采用了“无滑移边界条件”,即:固液交界面上没有滑移产生,亦即固体表面上的流体分子与固体表面的相对运动速度为0。然而研究发现无滑移边界条件假设在某些情况下不再成立,即边界滑移在低速、重载、窄隙等工况下会发生[1-2],并影响流体动力学行为。其中,边界滑移对水润滑轴承润滑性能的影响正受到越来越多的关注。研究表明,当2个表面具有不同极限剪切应力时,界面滑移会发生在极限剪应力较小的表面[3]。文献[4-5]提出了判别固-液交界面上产生界面滑移现象可能性方法:当润滑介质的界面张力大于摩擦副材料的界面张力时,即黏附断裂可能会出现在分子键的内聚断裂之前,此时界面滑移现象就会发生。一般地,低黏度润滑剂(如水),其分子间的黏附力远远小于其他常规润滑剂,因此在对非金属摩擦副材料或高分子摩擦副材料的水润滑轴承进行理论分析和实验研究时,应充分考虑到界面滑移可能对流体的动力学特性及轴承润滑性能产生的影响。国内外学者对此做了研究工作,如SPIKES[6]分析了轴承表面发生边界滑移时,边界滑移对轴承流体动力学行为的影响,结果表明当滑移表面的极限剪切应力等于0时,轴承流体动压承载能力恰好为无滑移时的1/2,但相应的摩擦力却降低了几个数量级。因此,SPIKES和GRANICK[7]提出了设计具有低摩擦因数轴承的思想,他认为边界滑移的存在使得轴承表面摩擦因数显著降低,但对轴承流体动压承载能力的影响比较复杂,与表面滑移性质(极限剪切应力大小)、表面粗糙度、运动状态以及轴承材料等有密切关系。MA等[8-9]研究了界面滑移对有限长滑动轴承动压性能的影响,发现各向均匀的滑移表面动压力会有所降低,对于极限剪切应力很低的滑移面,滑动轴承几乎没有承载力。而文献[10-13]研究结果显示复合边界滑移在使表面摩擦力降低的同时却使系统的流体动压承载能力显著提高,因此与无边界滑移表面相比,发生复合边界滑移时轴承在很大的间隙收敛率范围内都具有较高承载力,而发生均一边界滑移时承载能力较低。这就打破了经典的润滑理论[14]认为的只有收敛间隙才能使滑动轴承获得流体动压承载能力的理论框架,从而从理论方面为流体动力学领域的科研人员提出了新的思路和挑战。COTTIN-BIZONNE等[15]研究了光滑疏水表面界面滑移特性,讨论了光滑疏水表面较长滑移长度可能产生的原因,却忽略了就界面滑移对水膜压力、摩擦力等的影响做相应分析。以上这些研究结果和现象的提出充分说明了边界滑移问题的艰巨性和复杂性,其对轴承润滑性能的影响仍处于不甚清晰的状态。
另一方面,经典润滑理论认为雷诺方程右侧惯性力项很小,影响几乎可以忽略,如TICHY和CHEN[16]研究了平面滑动轴承在层流状态下考虑惯性力效应时的润滑性能,为了单独考虑惯性力效应,作者在较大的膜厚和低速工况下试验,研究结果表明在低雷诺数下惯性力效应的影响比经典理论中的预测结果要大;SAN ANDRÉS[17]研究表明在雷诺数较大的工况下,低黏度润滑介质黏性力与惯性力比值则小得多,惯性力的影响无法忽略。因此对水润滑轴承研究中充分考虑惯性力的影响还是很有必要的,且其对流体动力学特性的影响不甚清晰,有必要进一步深入探讨。
本文作者推导了适用于水润滑轴承综合考虑界面滑移和惯性力效应的修正雷诺方程,研究了水润滑轴承的润滑机制,求解得到水膜压力分布、膜厚分布及承载力、摩擦因数等参数变化规律,分析了界面滑移和惯性力效应对其润滑性能的影响,并与有限元结果对比,二者相互验证,说明理论分析的正确性。研究结果对于水润滑轴承的结构设计与计算具有一定指导意义。
1 雷诺方程的推导
根据分析,针对水润滑轴承的研究中,充分考虑界面滑移和惯性力效应的影响是很有必要的,目前尚无修正后的雷诺方程可直接应用。因此,这里首先推导直角坐标系下考虑界面滑移和惯性力效应的修正雷诺方程。
1.1 修正的雷诺方程推导
图1给出了水润滑轴承示意图,图1(a)是水润滑轴承截面图,图 1(b)是剖面展开图;图2给出了直角坐标系下水润滑轴承的简化示意图。假设表面2静止,表面1以速度u向右滑动,界面滑移发生在表面1,临界极限剪切应力为τc,临界滑移速度为uc。在分析中不考虑热效应,视为等温条件,即水膜厚度方向上水的黏度和密度不会随着温度而变化,恒为常值。除了等温条件,Reynolds方程推导过程中还需作如下假设:
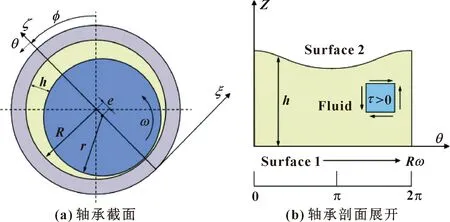
图1 水润滑轴承示意
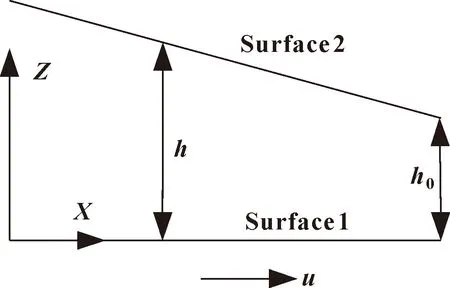
图2 简化水润滑轴承示意
(1)忽略体积力,如重力或磁力等的影响。

(3)水膜厚度方向上,不计压力的变化。
(4)与膜厚相比,支撑表面的曲率半径很大,忽略由表面曲率引起速度方向的变化。
(5)考虑惯性力效应的影响,但忽略流体加速时的惯性力和流体膜弯曲的离心力。
x方向动量方程:
(1)
边界条件:
表面1处,
z=0ux=u
(2)
表面2处,
z=hux=us
(3)
方程(3)对z积分2次并代入边界条件得
(4)
同理,可得y方向的速度
(5)
式中:Ix、Iy分别是x、y方向上的动量分量;ux、uy分别是x、y方向上的速度分量。
分别对方程(6),(7)积分可得x、y方向单位宽度上的体积流量:
(6)
(7)
由质量守恒定律:
(8)
代入并整理得:
(9)
其中,积分常数为
(10)
定义量纲一化参数如下:
(11)
得到修正的量纲一化雷诺方程为
(12)
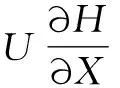
1.2 边界条件
采用自然破裂边界条件,即雷诺边界条件,该边界条件认为水膜不连续,水膜压力的终止是一种自然破裂现象,即在经过最小水膜厚度之后某一角度Y2处破裂,可以写为
雷诺边界条件与实际情况较接近,在研究中应用广泛。因此,文中采用雷诺边界条件进行求解得到水膜压力分布和膜厚分布。
水膜量纲一承载力可以通过对整个表面的压力分布进行数值积分获得,水膜量纲一摩擦力也可以通过对整个表面的剪切应力分布进行积分得到[18]。
1.3 数值求解
采用有限差分法求解修正后的雷诺方程,二阶中心差分离散偏微分项,并利用高斯-赛德尔迭代法进行求解,设置收敛精度为1×10-4。图3给出了计算的步骤流程。

图3 计算流程
2 结果与讨论
根据上述分析,滑动轴承压力、膜厚分布及润滑性能取决于长径比和偏心率2个参数,这里选取360°包角的有限长圆轴承进行分析。轴向网格取65,周向网格取65,偏心取0.8,长径比取0.8。水的界面极限剪切应力τc=1 806.5 Pa[5,21],计算时从水膜最薄处开始考虑界面滑移,即假设最小水膜厚度处最先出现界面滑移现象。
2.1 压力分布
水膜量纲一三维压力分布如图4所示,其中,X轴表示轴承的周向坐标,Y轴表示轴承的轴向坐标,Z轴表示水膜量纲一压力值。可看出,压力分布呈现抛物面形状,在水膜中间位置压力达到峰值。不考虑界面滑移和惯性力效应、仅考虑惯性力效应、仅考虑界面滑移以及综合考虑惯性力效应和界面滑移4种情况下水膜的周向压力分布如图5所示,图5(b)是压力分布的局部放大图。

图4 考虑界面滑移和惯性力效应的水膜压力分布

图5 水膜周向压力分布(a)及局部放大(b)
从图5中可以看出,考虑界面滑移和惯性力效应后对水膜的压力分布状态没有显著影响。界面滑移现象的存在明显降低了水膜压力峰值,随着间隙的减小,相应的水膜动压力增大,界面滑移效应越明显,水膜压力峰值减幅也越明显,最大减幅约为5%;惯性力效应的存在则略微增大了水膜压力峰值大小,随着间隙的减小,压力增幅扩大,但整体而言增幅很小,最大增幅仅约为0.16%;综合考虑惯性力效应和界面滑移情况下的水膜压力分布曲线在两者均不考虑和仅考虑界面滑移的曲线之间,数值更接近于界面滑移曲线,说明相对于界面滑移,惯性力效应对水膜压力的影响很有限,几乎可以忽略;同时,最大压力处亦即最小水膜厚度附近是最先发生界面滑移现象的区域,这是因为最大压力出现的区域界面所受剪切应力最大,相同条件下该处的剪切应力最先达到甚至超过界面极限剪切应力,发生黏附断裂从而产生界面滑移现象。
2.2 承载力
4种情况下水膜量纲一承载力随偏心率的变化如图6所示。
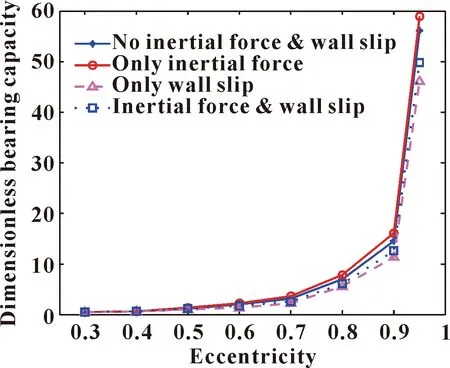
图6 水膜量纲一承载力随偏心率的变化
从图6中可以看出:界面滑移和惯性力效应不改变水膜承载力随偏心率变化趋势,随着偏心率的增大,水膜量纲一承载力逐渐增大;界面滑移现象则明显降低了轴承的承载能力,且随着偏心率增加降幅增大,最大降幅约3.5%;而考虑惯性力效应后,水润滑轴承的承载能力会略有增加,随着偏心率增加,增幅略微增加,但整体上增幅较小,最大增幅仅约1.75%;综合考虑惯性力效应和界面滑移情况下的承载力曲线在两者均不考虑和仅考虑界面滑移曲线之间,数值更接近于界面滑移曲线,说明相对于界面滑移,惯性力效应的影响几乎可以忽略。
2.3 摩擦因数
4种情况下水膜摩擦因数随偏心率的变化如图7所示。
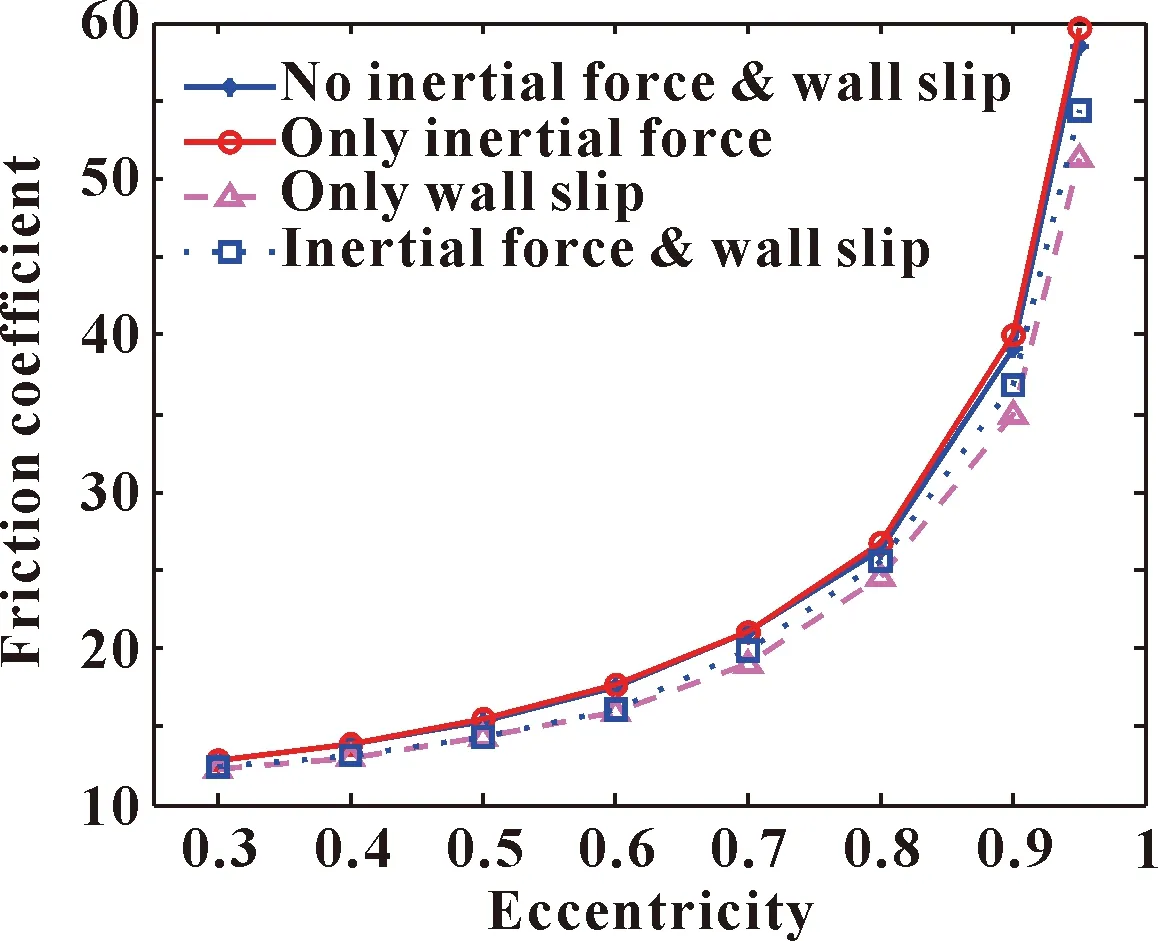
图7 水膜摩擦因数随偏心率的变化
从图7中可以看出:界面滑移和惯性力效应不改变水膜摩擦因数随偏心率变化趋势,随着偏心率的增大,摩擦因数增大;界面滑移的存在降低了水润滑轴承的摩擦因数,且随着偏心率增加降幅增大,最大降幅达到约10%,显然界面滑移可以明显减小水润滑轴承的摩擦因数,这也是水润滑轴承的一个重要优势;而考虑惯性力效应后,水润滑轴承摩擦因数会略有增加,而且随着偏心率增加,增幅略微增大,但受偏心率的影响不明显,整体上增幅较小,最大增幅小于1%,说明惯性力对摩擦因数的影响很小;综合考虑惯性力效应和界面滑移的摩擦因数曲线则介于二者均不考虑和仅考虑界面滑移曲线之间,数值更接近于界面滑移曲线,说明相比于界面滑移,惯性力效应对摩擦因数的影响要小得多,几乎可以忽略。
2.4 界面滑移的有限元分析
针对某实际水润滑轴承采用计算流体力学(CFD)软件进行建模分析,首先建立水膜模型,并针对模型进行网格划分、边界条件设置,然后进行有限元分析。水润滑轴承具体参数如表1所示,表2给出了20 ℃下水的基本物理参数。

表2 20 ℃下水的基本物理特性参数
一般而言,有限元分析中网格的质量起着决定性作用,文中经过反复几次迭代最终确定最佳网格质量。采用结构化网格,在边缘处进行网格的精细化和优化处理。入口和出口径向方向划分为5层,周向方向划分100段。在水膜模型的轴向方向,网格数量自动划分,划分段数一般与轴承长度密切相关。最终共划分节点17 952个,单元14 520个,具体如图8所示。
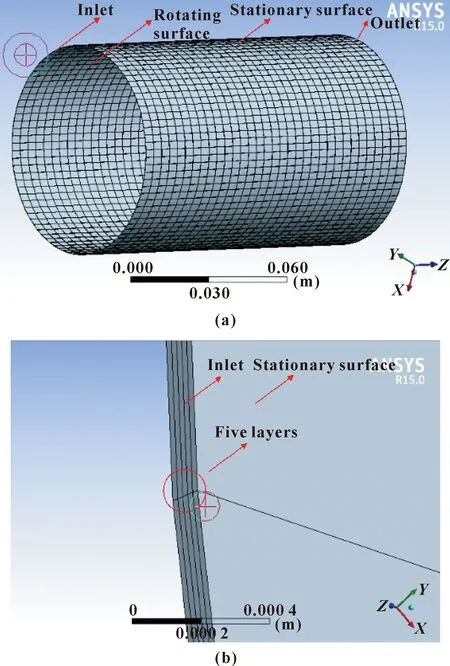
图8 动压水膜的网格模型(a)及局部放大(b)
图9给出了动压水膜模型及边界条件。假设楔形空间中的动压水膜为不可压缩、稳态和等温模型。在前处理软件中,建立轴承和轴颈表面的流动模型。

图9 动压水膜模型及边界条件示意
水的极限剪切应力为1 806.5 Pa[5,19],分别针对是否考虑界面滑移2种工况进行有限元仿真计算,并在后处理模块中提取压力分布云图如图10所示。
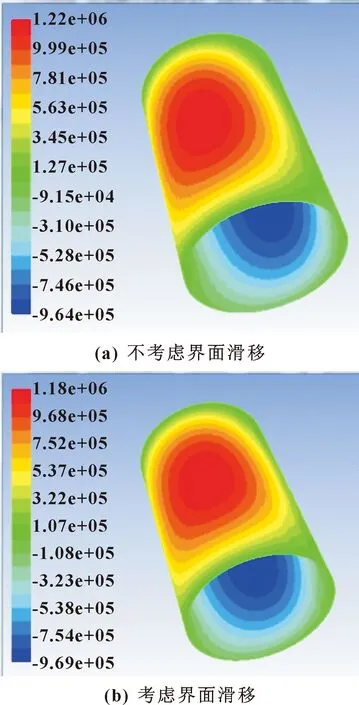
图10 水膜压力分布云图
同时,为更深入研究界面滑移对周向压力分布的影响,在水膜轴向中间点处建立等值面,提取该等值面与水膜曲面交线上的压力分布数值,导出正压区域压力数据,画出压力分布曲线,并与有限差分法计算结果对比,具体结果如图11所示。其中,No wall slip—FDM表示采用有限差分法计算不考虑界面滑移工况;No wall slip—Fluent表示采用有限元软件Fluent计算不考虑界面滑移工况;Wall slip—FDM表示采用有限差分法计算考虑界面滑移工况;Wall slip—Fluent表示采用有限元软件Fluent计算考虑界面滑移工况。

图11 水膜周向压力分布
从图11中可以看出,是否考虑界面滑移并不改变水膜压力分布整体轮廓,仅仅改变对应分布区域的压力数值,对应区域压力峰值明显降低,最大降幅约为5.2%,说明界面滑移的存在降低了压力数值;同时,界面滑移在最大峰值压力附近更为明显,这是因为最大压力出现的区域润滑界面所受剪切应力更大,相同条件下该处的剪切应力最先达到甚至超过界面极限剪切应力,发生黏附断裂从而产生界面滑移。有限元仿真结果与理论分析结果保持一致,二者相互验证说明理论模型的正确性。
3 结论
建立水润滑轴承流体动力学模型,推导了考虑界面滑移和惯性力效应的修正雷诺方程,通过数值求解探究了界面滑移和惯性力效应对润滑性能参数的影响规律,并与有限元分析结果对比,得出以下结论:
(1)界面滑移、惯性力效应对水膜的流体动力学特性有一定的影响。考虑界面滑移和惯性力效应的修正雷诺方程可以更完整地描述水润滑轴承的润滑状态以及润滑性能。
(2)界面滑移、惯性力效应并不改变润滑性能参数变化规律,仅改变其数值大小。界面滑移的存在降低了润滑性能参数数值大小,惯性力效应则略微增大润滑性能参数。相比于界面滑移,惯性力效应对水膜润滑性能的影响更小一些,几乎可以忽略不计。
(3)针对某实际水润滑轴承分别采用数值法和有限元法就界面滑移进行分析,结果表明:考虑了界面滑移后的压力峰值有所降低,二者相互验证说明文中模型的正确性。

