含对数项的分数阶T混沌系统滑模同步的3个控制方案

毛北行，王东晓

（郑州航空工业管理学院 数学学院，郑州 450046）

20世纪60年代，美国著名气象学家洛伦兹提出了第一个混沌系统模型［1］，即Lorenz 混沌系统，经过半个世纪的努力探索，学者们对混沌系统的特点和规律有了更清晰的认识，混沌系统的特性逐渐被发现，随后新的、经典混沌模型被相继提出［2-5］，并得出了更多有用结果［6-10］，例如：Chen 系统、Liu系统，T系统Qi 系和分数阶混沌系统.2004 年TIGAN 提出T 混沌系统［11］.王震等对其基本动力学分析与电路实现、同宿轨道、周期轨道的计算做了研究［12-13］.雷腾飞对含有指数项T混沌系统、四维T混沌系统、复T混沌系统做了系统研究［14］.随着研究的不断深入，李彪等提出一种新的含有绝对值项的混沌系统，雷腾飞以T混沌系统为研究对象，结合过渡临界T 混沌系统模型，提出了一类含有绝对值项的T混沌系统［15］，运用Matlab 仿真对系统的相图、分岔图、分岔空间等特性进行了分析.但与其他分数阶滑模同步的成果相比，分数阶T系统的成果较少，对于含有半导体器件的电路来说，研究带有对数项的T系统是非常有必要的.本文对含对数项的分数阶T混沌系统，给出了T混沌系统吸引子相图，在分数阶微积分的基础上，得到分数阶T 混沌系统取得滑模同步的3个控制方案.

1 系统描述

定义1［16］Caputo分数阶导

以下考虑分数阶含对数项T混沌系统

选取系统参数a=2，b=1，c=9，q=0.942，吸引子图如图1.

图1 系统（1）的相图Fig.1 The phase diagram of system（1）

设计（1）为主系统，从系统如下：

引理1［16-17］若x(t)为连续可微的函数，则有

引理2［18-19］设，若存在常数k＞0，使得DtqV(t) ≤-ky12(t)，则y12(t) ≤2V(0)Eq，1(-2ktq)且

2 主要结果

假设1|e3|≪|z|＜M,且z＞0.

定理1设计滑模面s(t)=Dtqe1+ae1，控制量

期中η＞0，则系统（1）与（2）滑模同步.

证明滑模面上有s(t)=0 ⇒Dtqe1=-ae1，⇒e1→ 0 ⇒Dtqe1→0.

根据（3）式的第1 个方程得到Dtqe1=a(e2-e1)⇒e2→0，下证e3→0.

引导定语从句的词有关系代词that，which，who（宾格whom，所有格whose）和关系副词where，when，why。关系代词和关系副词放在先行词和定语从句之间，起联系作用，同时又做定语从句的一个成分。

由（3）式的第3 个方程可得：x1y1-xy=x1e2-ye1.

因系统轨迹有界可知x1，y有界，故e1，e2→0时，x1y1-xy=x1e2-ye1→0，可得：

从而由引理2 不难得到s(t)→0，因此系统（1）与（2）滑模同步.

定理2设计滑模面s(t)=e2+e1，控制量

其中常数η＞0，则系统（1）与（2）滑模同步.

证明滑模面上有s(t)=0 ⇒e2=-e1，根据（3）式的第1个方程可得：

从而由引理2 不难得到s(t)→0，因此系统（1）与（2）滑模同步.

定理3设计滑模面s(t)=e2，控制量

其中常数η＞0，则系统（1）与（2）滑模同步.

证明滑模面上有s(t)=0 ⇒e2→0，根据（3）式的第1个方程有Dtqe1=-ae1

⇒e1→0，同理可证e3→0，过程同定理1，略.

从而由引理2 容易得到s(t)→0，因此系统（1）与（2）滑模同步.

3 数值仿真

选取系统参数a=2，b=1，c=9，q=0.942，定理1～定理3中的误差见图2～图4.

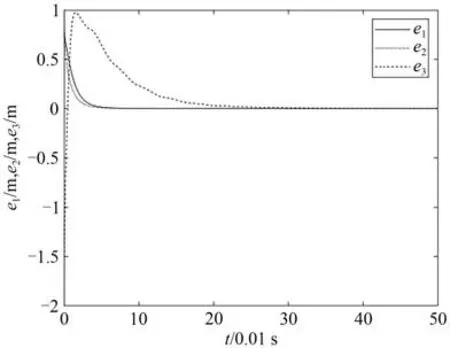
图2 定理1的误差Fig.2 Errors in theorem 1

定理1～定理3 分别构造滑模面s(t)=Dtqe1+ae1，s(t)=e1+e2，s(t)=e2.设计控制量分别为：

取定初始值 (x(0)，y(0)，z(0))=(2，2，5)，(x1(0)，y1(0)，z1(0))=(3，3，3)，η=1.

由图可知，初始时误差相差较大，在时间的变化下系统误差最终趋于坐标原点，表明误差趋近于0，定理1、定理2 取得同步所需时间比定理3 长，定理1、定理2 取得同步的时间没有太明显的差别，但是定理1 比定理2 的控制器要复杂，所以需要消耗较大的能量，而定理2则控制代价小容易实现，且定理1中误差振幅较定理2大，因而定理1的抖振现象可能较为明显，另外从图2、图3、图4 可看出，3 个定理的控制效果越来越优良.

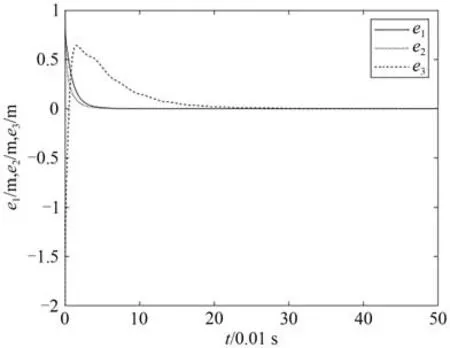
图3 定理2的误差Fig.3 Errors in theorem 2

图4 定理3的误差Fig.4 Errors in theorem 3

4 结语

根据滑动模态控制理论和分数阶微积分的相关理论，本文研究了含对数项的分数阶T 混沌系统滑模同步的3 个控制方案.利用分数阶稳定性理论给出了详细的证明过程，并对所得结果进行了验证.以上研究为该类混沌系统的同步控制提供了一些新思路.