结合改进聚类算法与PSO-GA-BP神经网络算法的日最大负荷预测方法

李威武，白永利，罗世刚，许青

（1 国网甘肃省电力公司经济技术研究院，兰州 730030；2 国网甘肃省电力公司，兰州 730030）

电力负荷预测是指以地区历史负荷、天气等外界影响因子为依据，开展研究分析，通过采用数学方法或建立数学模型的方式，对电力系统的需求做出估计［1］.准确的电力负荷预测是电力系统安全、稳定、经济运行的保障，也是电网进行规划调度的重要依据.日最大负荷预测通过对未来数月甚至数年的单日电力负荷峰值进行预测，判断电网网架结构对未来数月甚至数年的负荷承载能力，以此为电网规划及电网项目投资提供指导意见［2］.

随着“双碳”政策的开展及智能电网建设的进一步深入，当前电网分布式电源渗透率显著提升，地区电网日最大负荷愈发易受外界环境因素的影响，为地区电网负荷预测工作带来一定难度.因此参考地区历史负荷水平，结合地区环境变量诸如温度、湿度、节假日等因素，对历史日进行合理分类，为数学模型提供高质量训练集，是提升日最大负荷预测精度的有效方式之一.

借此思路，文献［3］提出一种结合纵横交叉算法参数优化的鲁棒极限学习机算法，以建立负荷的多分段预测模型，分段依据由聚类与CART 树相结合的方法确定；文献［4］将模糊C均值聚类结果进行变分模态分解，以构建神经网络模型的输入；文献［5］采用灰色关联分析方法选取相似日粗集，再对相似日粗集的外部因素进行聚类分析，划分相似日集合，最终利用相似日集合训练长短期记忆（Long-Short Term Memory，LSTM）神经网络，进行负荷预测；文献［6］采用动态时间规整算法计算行业电量周期性，聚类得到相似用电特性的行业电量序列，最后针对各电量子序列建立支持向量回归模型；文献［7］综合考虑经济、气象等因素，以计量经济学中的协整检验以及格兰杰因果检验分析确定负荷关键影响因子，采用支持向量机进行月负荷预测.文献［8］提出均值漂移概念，以解决模糊C均值聚类算法无法确定聚类数目的问题，在分解负荷分量后，运用XGBOOST完成最终预测.

纵观上述研究，基于深度学习算法的负荷预测模型的精准度很大程度取决于学习样本的质量.合适的聚类算法能有效保障相似日的代表性，大大提升负荷预测模型的可靠性［9］.现有预测模型所应用的聚类算法，如模糊C均值算法、K-means算法等，大多存在聚类数目需人为指定、初始聚类中心选取随机、聚类过程易受畸变数据影响等问题，算法聚类结果不稳定、聚类质量较低，从而影响负荷预测结果的精准性.

为解决此问题，本文提出一种基于中心度的改进聚类算法（Cen-CK-means 算法），对神经网络算法的学习样本进行优化.首先，基于数据集中各对象的中心度，筛选聚拢效果最优的对象作为初始聚类中心集的第一类中心；然后，采用Canopy 算法确定初始聚类中心集，并基于K-means 算法，得到不同类别相似日集合；最后，以不同类别相似日集合作为训练样本，构建PSO-GA-BP 神经网络算法拓扑结构，进行日最大负荷预测.算例结果表明，本文所采用聚类方法具备更好的综合性能，能为神经网络算法提供质量更高的相似日学习样本，从而获取更准确的日最大负荷预测结果，满足电网系统调度规划需求，具有一定工程实用价值.

1 算法介绍

1.1 Cen-CK-means算法

1.1.1 中心度概念

传统Canopy 算法能在无需给定聚类数目的前提下，以较快速度实现对被聚类对象的分类划分，常用作确定精准聚类算法（如：K-means 算法）的初代聚类中心［10］.但由于算法初始聚类中心选取过程较为随机，算法聚类质量不甚稳定，一定程度影响后续精准聚类算法的精准度［11］.

为改善Canopy 算法初始聚类中心选取过程，本文综合考虑被聚类对象的密度分布与距离因素，引入中心度（Cen）的概念，对以各对象作为聚类中心的类别集合作聚拢度分析，并以此为依据，研判被聚类集合中各对象作为聚类中心的优先度.中心度数值越小，表明对象作为聚类中心的优先度越高.

设定距离阈值参数（H），对具有n个聚类对象的被聚类对象集合D=(D1，D2，…，Dn)开展中心度分析：计算各被聚类对象Di，以自身为圆心，H为半径的圆内，所覆盖其他被聚类对象与圆心的标准化后的平均距离，如图1所示.

图1 中心度聚拢效果图Fig.1 Centrality aggregation effect

具体计算过程如下：

首先，以被聚类集合所有对象之间的平均距离Ave(D)作为对象类别划分的阈值参数，如式（1）所示，若对象间的距离在阈值参数内，即视作同一类；

式中，d(Di，Dj)为被聚类对象Di与Dj之间的欧氏距离.

然后，对D=(D1，D2，…，Dn)中的每个被聚类对象Di进行密度Ai的计算，如式（2）所示.

式中，函数W(x)表达式如式（3）所示.

最后，根据式（4），计算每个被聚类对象Di的中心度Ceni，得被聚类集合D的中心度矩阵Cen=(Cen1，Cen2，…，Cenn).

其中，Si为各对象间距离标准化后的数值，如式（5）所示.

其中，min(Di)表示以Di为聚类中心的聚类类别中所有对象，与Di最近的距离；max(Di)表示以Di为聚类中心的聚类类别中所有对象，与Di最远的距离.

1.1.2 基于中心度的Canopy算法

基于中心度的Canopy 算法（Cen-Canopy 算法），加入对各对象的中心度前置计算，作为第一个聚类中心的选取依据.同时，算法在最后得到所有聚类结果后，对所含对象数量较少的类别作噪声进行删除处理，以避免个别异常数据，对整体聚类质量产生影响.

算法具体运行流程如下：

（1）设定阈值T，T取被聚类集合D=(D1，D2，…，Dn)所有对象之间的平均距离Ave(D)；

（2）对被聚类对象集合D=(D1，D2，…，Dn)开展中心度计算，得Cen=(Cen1，Cen2，…，Cenn)，并按照从小至大进行排序；

（3）选取中心度最小的对象Di作为Canopy（Si），并将所有满足d(Dj，Si)＜T的对象Dj归为此Canopy类别，并从集合D中删除；返回步骤2），重新计算剩余对象的中心度，直至集合D中数据为空.

（4）对于算法所得所有的Canopy 类别，若类中类内对象个数小于，则将此类数据作噪声处理，进行删除.

1.1.3 算法实现过程

本文算法实现过程的具体流程如图2 所示.对于具有n个对象m个特征维度的被聚类数据集D=(D1，D2，…，Dn)（其 中，Di=(Di，1，Di，2，…，Di，m)），首先，基于被聚类集各对象的中心度，选取第一个聚类中心；然后，以此为基础，基于Canopy 算法确定聚类数目与初始聚类中心；最后，将初始聚类结果代入基于中位数的K-means 算法，进行聚类运算，得到最终聚类结果.具体步骤如图2所示：

图2 改进聚类算法流程图Fig.2 Improved clustering algorithm flowchart

（1）预处理.对被聚类数据集D中各被聚类对象中各维度特征进行归一化处理［12］，如式（6）所示，得到归一化数 据集Y=(Y1，Y2，…，Yn)（其中Yi=(yi1，yi2，…，yin)）.

式中，max(Dj)、min(Dj)分别表示被聚类对象集合第j个特征的最大值与最小值.

（2）初始化.首先，根据式（1）～（4），计算各被聚类对象的中心度值，选取中心值最小的对象作第一个聚类中心C1；然后，采用Canopy算法，以平均距离Ave(Y)为阈值，确定其余聚类中心，得到初始聚类中心个数L及初始聚类中心集合的矩阵C=(C1，C2，…，CL)T.设定算法迭代次数I.

（3）相似度衡量.对被聚类对象关于每类聚类中心进行基于欧氏距离的相似度计算，根据相似度值（相似度值越小，表明越相似），将对象分至最相似的类别中.

（4）聚类中心更新.本文不同于传统方法通过类别平均值进行聚类中心更新，是通过选取每一类别中的各被聚类对象各维度的中位数值作为新一代聚类中心：对于每一维度进行数值大小排列，取各维度中位数，作为新聚类中心的更新值.当算法满足以下任一条件时，跳出迭代程序，输出最终聚类结果：1）聚类离散度运行至收敛，即|JI+1-JI|＜e，如式（7）所示；2）聚类中心不再随迭代次数增加而发生变化.否则，跳转至步骤3），直至算法满足跳出迭代条件或运行至最高迭代次数I.

式中CL(I)为算法进行第I 次迭代后的第L 类的聚类中心，Yn表示属于L这一类的负荷曲线.

1.2 聚类有效性指标

聚类质量较高的聚类结果，一般具有同类别集合具备较强相似性，而不同类别集合具有较强差异性的特点.本文参考文献［13］，引入DBI 指标，通过计算类内距离之和与类外距离的比值，对聚类算法的聚类效果作出评价，指标值越小，聚类效果越好，如式（8）-（9）所示.

式中，Ri用来衡量第i类与第j类的相似度.

式中，Si用以衡量第i类集合内对象的相似度，Mij用以衡量第i类集合与第j类集合中对象的的差异度.

定义I1，以欧氏距离为度量方式，评估聚类结果各类别集合数据的分布特性；定义I2，以动态时间弯曲距离为度量方式，评估聚类结果各类别集合数据的形状特性.

1.3 PSO-GA-BP神经网络算法

BP 神经网络作为目前应用最广泛的神经网络模型之一，拥有非线性映射能力、自适应能力及泛化能力等优点［14］.但由于算法采用梯度下降法，算法优化过程中较易出现局部极小化、收敛速度慢、过拟合及隐含节点数目难以确定等问题［15］.

本节通过引入兼具全局收敛与收敛速度较快特点的PSO-GA 混合算法，形成PSO-GA-BP 神经网络算法，可以很大程度上提升算法收敛速度，避免陷入局部最优，提升算法的综合性能.算法具体流程如图3所示.

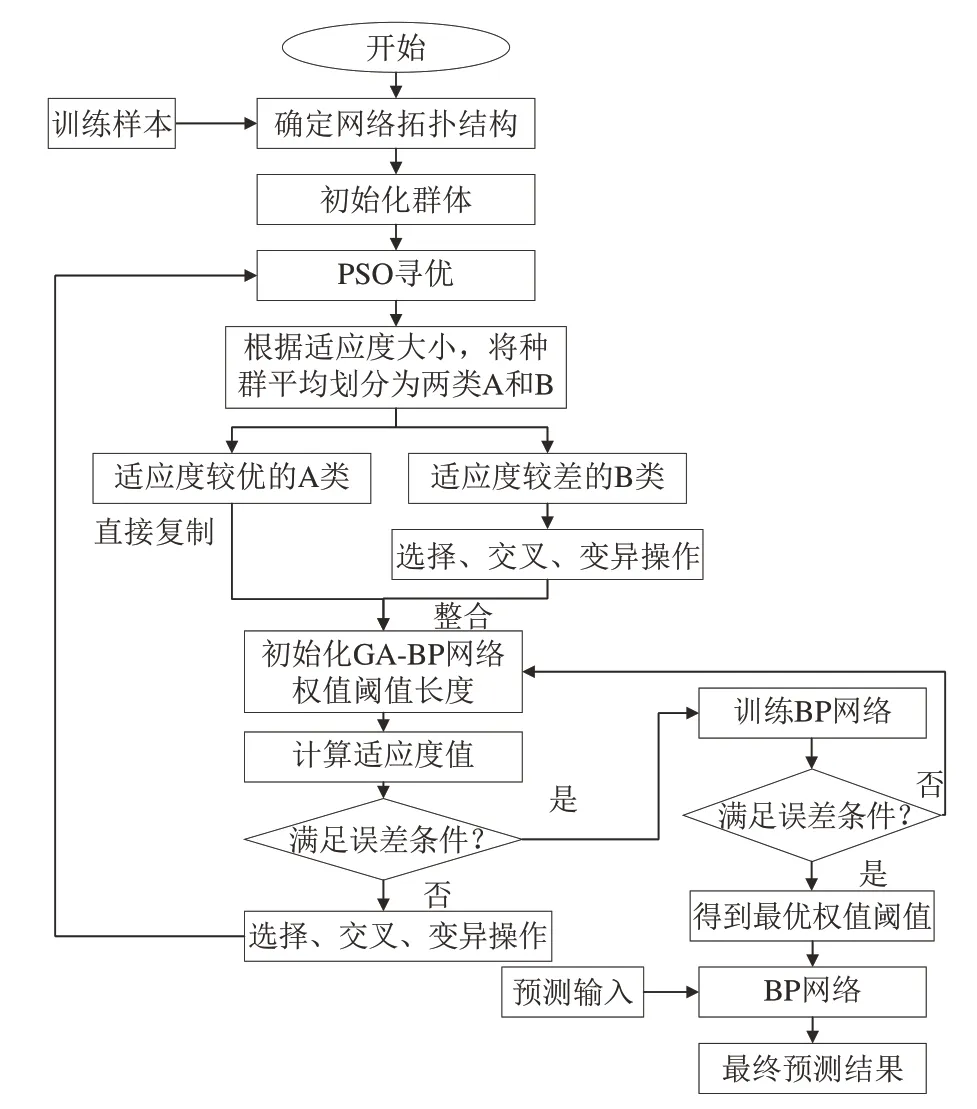
图3 GA-BP神经网络算法流程图Fig.3 Improved clustering algorithm flowchart

2 基于PSO-GA-BP 神经网络的预测模型

2.1 负荷影响指标体系

首先，构建此10个负荷影响指标近一个月内的日变化曲线集T=(T1，T2，…，Tn)，其中Ti=(Ti，1，Ti，2，…，Ti，30)表示第i个指标的日变化曲线，Ti，j表示第i个指标在一个月内第j天的指标；

然后，对T中各指标的日变化曲线关于近一个月的日最大负荷变化曲线P=(p1，p2，…，pn)进行皮尔森相关系数分析，如式（10）所示，若|ρ(Ti，P)| ＜0.4，则第i个影响指标Ti与日最大负荷呈现弱相关关系，不纳入最终负荷影响指标体系；

其中，Cov(X，Y)表示序列X与Y之间的协方差，如式（11）所示；σX表示序列X的标准差，如式（12）所示.

其中，E(X)表示序列X中所有元素的平均值.

最终，对于筛选出的k个指标T=(T1，T2，…，Tk)，构建每日的负荷影响指标曲线集U=(U1，U2，…，U30)，其中Ui=(Ui，1，Ui，2，…，Ui，n)表示第i天的负荷影响指标集，并根据式（6）对Ui中的第j个指标元素Ui，j进行归一化处理.

2.2 日最大负荷预测模型

结合Cen-CK-means 聚类算法与PSO-GA-BP 算法，搭建日最大负荷预测模型，如图4 所示.预测模型分为两大模块：

图4 日最大负荷预测模型图Fig.4 Daily maximum load forecasting model diagram

（1）训练模块：对历史数据库中的负荷影响因素集进行关于日最大负荷数据的皮尔森相关系数分析，形成有效负荷影响因子集合.对所形成的集合采用Cen-CK-means 聚类算法，得到不同类别的相似日集合，并以此作为训练样本的输入，将对应的日最大负荷数据库作为训练样本的输出，通过GABP神经网络算法形成不同类别相似日的预测模型.

（2）日最大负荷预测模块：根据预测日负荷影响因子数据，将预测日划分至对应类别相似日集，输入对应相似日类别的负荷预测模型，输出待预测日的日最大负荷数据.

2.2 香菇普通粉与香菇超微粉色差比较 经色差仪测定，香菇普通粉的L*值为68.67，香菇超微粉的L*值为74.91，两者之间存在显著性差异(P<0.05)，表明香菇粉粒度越小，粉体的亮度越高。在实际生产中，可以通过减小香菇粉粒度提高其色泽。

2.3 预测结果评价指标

本文采用平均绝对误差百分比（Mean Absolute Percentage Error，MAPE）与均方根误差（Root Mean Square Error，RMSE）对日最大负荷预测结果的精准度进行评估［17］.

其中n为预测序列中预测对象个数，为第i个预测值，yi为第i个实际值.

3 算例分析

为验证本文所提方法预测效果，对处于北温带四季分明的某地区开展日最大负荷预测分析.地区负荷影响因子数据集采样时间为2011 年1 月1 日-2012 年12 月31 日，其中，历史负荷因子采样间隔为30分钟，温度、湿度、降雨量等天气因子采样时间间隔为1天.

算例将2011年数据作为训练样本，2012年数据作为测试样本，以聚类指标、预测指标作为评判依据，将本文方法与方法1、方法2进行对比分析，以验证本文所提方法的优越性.三种方法所采用负荷预测方法一致，差别主要聚类算法：方法1采用传统聚类方法K-means 算法；方法2 采用基于Canopy 的Kmeans 算法，基于Canopy 算法选取的初始聚类中心进行聚类运算；本文算法在Canopy 算法的基础上基于中心度选取初始聚类中心.具体如下所示：

方法1：K-means-PSO-GA-BP方法.

方法2：CK-means-PSO-GA-BP方法.

本文方法：Cen-CK-means-PSO-GA-BP方法.

算例运行环境：单台计算机，配置为i7-1165G7@2.80GHz，MX450 2G，操作系统为Windows 10，内存为16G.

3.1 负荷影响因素集合

参考文献［16］所选取采用的负荷影响因子，构建预测地区10 个负荷影响指标近30 天内的日变化曲线集R=(R1，R2，…，R10).对曲线集中的每条曲线关于日最大负荷变化曲线P=(p1，p2，…，p30)进行皮尔森相关系数分析（皮尔森相关系数值介于-1 与1之间，绝对值越接近1，表示线性关系越强），如表1所示.本文认为若某负荷影响指标的相关系数绝对值大于0.4，则认为该负荷影响指标为强负荷影响因子，在负荷预测模型中予以采用.

表1 负荷影响因子的皮尔森相关系数表Tab.1 Daily maximum load forecasting model diagram

通过筛选，得到最终的地区负荷影响指标体系T=(T1，T2，…，T8)，分别为最高温度，最低温度，平均温度，相对湿度，前一天最大负荷，前两天最大负荷，前三天最大负荷，去年同日最大负荷.

3.2 聚类分析

根据负荷影响因子指标体系T，构建被聚类数据集，分别运用本文方法、方法1 与方法2 中的聚类算法对数据集进行5 次聚类分析，取其中聚类质量最优的一组聚类结果作为最终聚类结果进行展示.

各方法5 次运算的初始聚类中心质量如图5 和图6 所示.由于方法1 为传统方法，初始聚类中心选取完全随机，故初始聚类中心的选取质量变动较大；方法2基于Canopy算法进行初始聚类中心选取，由于对第一个聚类中心的选取仍存在随机筛选，故初始聚类中心质量仍不完全稳定；本文算法相比方法1和方法2，基于中心度严格对初始聚类中心集进行筛选，选取结果稳定，且综合质量最优.

图5 不同方法的初始聚类结果的I1指标Fig.5 I1 indicator of initial clustering results of different methods

图6 不同方法的初始聚类结果的I2指标Fig.6 I2 indicator of initial clustering results of different methods

根据图5-6 的初始聚类中心集，本文方法、方法1 和方法2 的最终聚类结果如图7～9 所示的聚类结果.不难发现，三种聚类方法所得聚类中心曲线相似度较高.

图7 本文方法聚类结果Fig.7 The clustering results of the proposed method

图8 方法1聚类结果Fig.8 The clustering results of method 1

图9 方法2聚类结果Fig.9 The clustering results of method 2

第一类曲线的负荷影响因素曲线集主要反映的是6-9 月的夏季典型负荷日的负荷影响集：地区温度较高、湿度相对较低，且负荷维持在较高水平；第二类曲线的负荷影响因素曲线集主要反映的是2-4 月的春季典型负荷日的负荷影响集：地区温度较低、湿度相对较高，但负荷维持在较低水平；第三类曲线的负荷影响因素曲线集主要反映的是11-1月的冬季典型负荷日的负荷影响集：地区温度较低、湿度相对较高，但负荷维持在较高水平；第四类曲线的负荷影响因素曲线集主要反映的是5月与10月的初夏及初秋典型负荷日的负荷影响集：地区温度较高、湿度相对较高，但负荷维持在较高水平.

各方法聚类指标和运算过程的聚类离散度变化情况分别如表2 和图10 所示.本文方法虽运算时间略长于其他两种方法，但算法迭代次数最少，综合聚类质量更优.这主要由于本文算法在进行聚类运算之前，采用基于中心度的Canopy 算法选取初始聚类中心，故耗时相对更长，但也因此获取了更高质量的初始聚类中心（本文方法的初始聚类中心聚类质量和聚类离散度均优于另外两种方法），加速了后期K-means 算法的聚类速度，使算法经过更少迭代即能获取聚类质量更高的聚类结果.

表2 各类方法聚类指标表Tab.2 Cluster indicator table for various methods

图10 各类方法聚类离散度变化情况Fig.10 Changes in clustering dispersion of various methods

3.3 预测分析

为验证本文方法所得聚类结果对于最大负荷预测精准度提升的效果，本文将三种聚类算法所得聚类结果作为学习样本，对应日最大负荷作为输出，采用PSO-GA-BP 算法搭建日最大负荷预测模型.对从2013 年随机选取的各季节共84 天的最大负荷进行预测分析，预测结果如图11～13所示.

图11 本文方法预测结果Fig.11 The predicting result of the proposed method

图12 方法1预测结果Fig.12 The predicting result of method 1

图13 方法2预测结果Fig.13 The predicting result of method 2

由图11～13 及表3 可知，本文所提聚类方法精准度更高，负荷影响因子集合划分更准确，能够为深度学习提供更优质的学习样本，从而得到更高质量的预测模型，故在相同深度学习算法下，本文方法所得最大负荷的预测结果的两项预测指标（MAPE=5.71%，RMSE=4.94 MW），均优于方法1 与方法2.

表3 各类方法预测指标表Tab.3 Table of prediction indicators for various methods

综上所述，本文所提方法较其他方法，在聚类质量、预测精准度等方面具有更优的综合性能，具备实际工程应用价值.

4 结论

为优化负荷预测模型相似日训练样本质量，提升预测精度，本文提出一种基于中心的的改进聚类方法，对历史日根据有效负荷影响因子特征进行相似日集合划分，并基于PSO-GA-BP 神经网络算法搭建日最大负荷预测模型.算例表明：

（1）基于中心度的Canopy 算法选取初始聚类中心的方法采用合理.其能够准确评估被聚类对象集中各对象的聚拢度，准确选取最具代表性的数据集作为初始聚类中心集.

（2）本文所提聚类算法具备更优的综合性能，能根据负荷影响因子对历史日进行精准划分，形成不同类别相似日集合，为神经网络算法提供更准确的学习样本，提升日最大负荷预测结果的精准性.

未来将纳入更多负荷影响因子，建立更健全的历史负荷影响因子数据库，进一步提升日最大负荷预测结果的准确性与合理性，以对电网的规划与调度形成更有效的支撑.