融合多因素的多实体政策网络链路预测算法

陈慧敏，康怡琳，刘浩，朱容波*

（1 中南民族大学 计算机科学学院，武汉 430074；2 华中农业大学 信息学院，武汉 430074）

政策文本为社会的发展提供了权威性、原则性的指导和方向，对社会发展产生了极大的影响.然而，随着中央和地方政府政策文本的不断发布，一方面由于政策文本繁多且分布在各部门网站系统中，较为分散，难以流通共享，导致相关政策浏览受阻；另一方面，由于政策的专业性与民众知识的限制，大多数民众难以准确全面获取自己想要了解的政策信息.此外，与普通文本不同，政策文本的结构相对多样，政策文本之间的信息通常是离散的，并没有明确连接的关系［1］.一篇政府政策基本包含3种类型的实体：政策标题、发布此政策的部门和此政策所涵盖的主题.实体之间存在着各种类型的关系：政策与部门之间的发布关系、部门之间的合作发布关系、政策与主题之间的涵盖关系，构建多实体政府政策网络需要考虑直接和间接的关系，多实体节点之间的关系要比单实体更加复杂和多样化.因此，如何快速准确地从海量政策中找出相关的政策文本值得深入研究.

链路预测通过已知信息预测尚不存在关联的两个节点潜在连接关系的可能性，在社交网络［2］、司法案件推荐［3］、动态网络［4］、生物医学［5］方面有广泛应用.通过对政策网络进行链路预测来挖掘政策间的相关性、部门间的协同性，将政策间、部门间关系显性化，不仅为政策发展演化与政策制定提供了科学依据，有效地促进了部门间协同合作，也为民众提供了更全面准确的政策推荐服务，满足了不同主体的政策诉求，扩大了政策的普及范围，实现了主动化服务.例如某大学生准备返乡创新创业，在省人民政府浏览创新创业政策后，会推荐给该主体关于财政厅如何从财政上支持大学生返乡创新创业.

但由于交叉学科以及相对专业，目前针对政策文本的链路预测现有工作相对较少，现有的链路预测方法主要分为基于结构相似性的方法［6-7］和基于矩阵分解的方法［8-9］.基于结构相似性的方法由于方法简单，计算信息易于获取，复杂度相对较低.然而，现有的基于结构相似性的方法大多从所预测节点对之间的共同邻居节点信息出发，难以充分表示网络的信息，导致预测精度偏低.基于矩阵分解的方法考虑了网络中的拓扑结构信息，将网络矩阵分解为低维矩阵，适用于数据稀疏的网络，具有较高的预测精度.但该方法没有捕获节点连接偏好以及综合利用局部和全局信息，不能很好地分析政策并对政策网络进行链路预测.因此，在面对政策文本时，如何从复杂的政策中有效地获取政策中的重点信息以及如何通过链路预测对政策间的关系进行预测具有挑战性.

针对现有工作较少、政策文本间关系错综复杂、政策实体间潜在连接关系隐性、多实体政策网络数据稀疏、网络节点属性丰富等特点，以及现有研究大多集中于单一类型的政策实体及关系，难以全面准确地刻画政策间多类实体潜在关系的不足，本文考虑从节点相似出发，提出了一种融合节点相似和属性偏好的多实体政策链路预测算法（Link Prediction via Node Similarity and Attribute Preference，LP-NA）.LP-NA 以反映局部信息的链接聚类系数［10］和全局信息的接近中心性［11］来计算节点相似度，构建原始权重矩阵，并将政策网络的节点属性偏好和预测偏离值融入矩阵分解框架中，对网络中已知连边信息进行综合计算，提升了链路预测的准确性，可有效地为民众提供服务.

1 多实体政策网络链路预测算法

1.1 问题描述

传统链路预测算法大多是利用共同邻居节点个数、共同邻居节点度值或聚类系数等节点信息对节点间连边概率进行预测，未考虑到数据集特征对预测结果的影响.基于此，从政策网络数据集的特性出发，本文提出了一种融合节点相似和属性偏好的多实体政策网络链路预测算法LP-NA.LP-NA 首先从收集到的政策文本数据集，获取其所包含的实体及关系，构建一个多实体政策网络，然后通过已知网络中的相关信息、网络的相关局部特征、全局特征和潜在特性的分析，利用矩阵分解的思路对网络节点间的链路进行预测，系统流程如图1所示.

图1 系统流程图Fig.1 Flow chart of system

针对政策网络进行链路预测计算，包括通过构建融合节点相似的原始权重矩阵，计算不同节点间的连接属性偏好和预测值偏差，根据LP-NA 算法计算节点间连接预测值，其目标函数为：

其中，Ek表示网络中已知节点对连边集合，Rij表示权重矩阵中的值，Hi与Hj表示同一类网络节点i和j的特征向量，β表示防止过度拟合化参数.公式（1）将权重矩阵分解为两个相同的节点特征矩阵，通过分解后得到的矩阵乘积，再将属性偏好以及预测偏差值融入计算从而构建一个新的相似概率矩阵sim，根据相似概率矩阵sim中的取值对节点间产生连边的可能性进行预测.本文所提出的预测方法融合了更多因素，可以更好地挖掘出节点之间的潜在关联，得出更准确的预测.

1.2 多实体网络的构建

本文将多实体政策网络建模为一个异构图，定义多实体政策网络为：G(VD，VP，VT，E)，其中，VD={D1，D2，…，Da}、VP={P1，P2，…，Pb}和VT={T1，T2，…，Tc}分别代表政策发布部门、政策标题和政策主题；E表示边的集合.在网络中定义了两种类型的边：同构实体边和异构实体边.同构实体边是连接相同类型的两个节点的边，例如E(D1，D2)表示部门1和部门2由同构实体边连接，它们是相同类型的实体；异构实体边即连接的两个节点属于不同的类型，例如E(D1，P1)表示部门1 与政策标题1 由异构实体边连接.本文构建多实体政策网络（Multi-Entity Policy Network，M-EPN）的框架如图2所示，具体步骤如下：

图2 M-EPN框架Fig.2 M-EPN framework

（1）数据采集.本文以中国政府官网公开发布的政策文本作为研究数据集，在政策选择时，邀请专业人员来分析数据源，剔除不相关的政策.对政策数据集预处理是保证数据质量的重要操作，通过删除每篇政策中的噪声数据，以确保获得的主题的质量.此外，考虑到政策内容的非结构性，本文将政策重命名为原政策标题的格式加上相应的部门名称，便于政策标题及部门的提取.如：《关于做好2020 年电子商务进农村综合示范工作的通知》_财政部办公厅+商务部办公厅+国务院扶贫办综合司.

（2）实体及关系的提取.在构建多实体政策网络之前，必须提取政策中包含的实体及关系，针对主题的提取，本文采用最流行的方法之一Latent Dirichlet Allocation（LDA）主题模型［12］获取政策主题.LDA假设一个单词属于一个主题，并且一个文档在这个过程中至少属于一个主题.因此，有一个二维数组来显示每个政策所包含的主题，这意味着政策标题与主题之间的对应关系被挖掘出来.在构建模型之前需要确定参数Z值，它表示政策中包含的主题数量.困惑度是用来评估模型泛化能力的指标，其值越低模型的泛化能力越强.本文利用困惑度确定了最优主题数Z.在LDA 模型中，困惑度是指文档d属于训练模型所确定的特定主题的不确定性程度.困惑度得分越低，模型对文档d主题的推断就越准确.对于M个文档的数据集，困惑度计算［12］如公式（2）所示：

式中：D表示所有文档的集合，M表示文档的数量，Nd表示第d个文档中的单词数，tj表示第j个主题，P(wi|tj)表示单词wi出现在第j个主题中的概率，P(tj|d)表示第j个主题出现在第d个文档中的概率.在政策数据集中，每篇政策的标题是唯一的，但其发布部门的名称可能与其他政策的发布部门相同.因此，在使用正则表达式提取标题和部门后，还需要对部门实体去重以保证唯一性.

（3）构建多实体政策网络.通过实体及关系的提取，建立了政策标题、部门和主题之间的对应关系，本文将不同的实体及关系视为三元组，使用Python将获得的实体及关系编码到一个多实体的政策网络中.

1.3 LP-NA算法

为了解决稀疏数据中网络潜在特征信息挖掘的难题，LP-NA算法融合了节点的多属性信息，包括节点的链接聚类系数、接近中心性值以及对不同属性节点偏好等信息.将上述网络信息融入到矩阵分解的框架中，能够很好地解决政策网络稀疏性的问题，从而更好地挖掘出政策网络中的潜在关联信息.

LP-NA 算法框架如图3 所示，首先将政策网络用矩阵形式表示，通过计算节点间吸引力Si，j，构建权重矩阵Rn×n，通过矩阵分解方法将权重矩阵Rn×n分解为两个相同的矩阵A，使得Rn×n≈AAT，再融入不同节点属性偏好Ci，j以及预测偏差值Di，j，利用矩阵分解中乘法更新规则更新权重矩阵Rn×n中的值，得到节点间连边的预测值.

图3 LP-NA算法框架图Fig.3 LP-NA algorithm framework diagram

1.3.1 权重矩阵的构建

政策网络中不同的节点自身拥有的资源不同，对其他节点的吸引力也不同，导致节点间连边的重要程度也不同.对于权重矩阵的构建，首先定义已知节点间连边的重要程度.

现有的节点间的连边重要程度预测方法未考虑被预测节点与其共同邻居节点之间连边的紧密程度，如图4（a）所示，节点B与节点C的度值相等且共同邻居个数都为1，但节点A与C之间的吸引力显然比节点A与B之间的吸引力要高.本文充分利用共同邻居的节点信息和共同邻居与节点对之间的信息，采用链接聚类系数评估两节点之间的结构信息.对于图4（b）来说，如果节点A与E相连，节点C与E相连，与图4（a）相比可以看到节点之间的平均最短路径缩短，这说明网络中的平均最短路径对节点间是否可能产生连边有较大的影响.接近中心性计算每个结点到其他结点的最短路径的平均长度，衡量节点间的接近程度.即对于一个结点而言，距离其他结点越近，其接近中心性值越高，越可能与尚未连边的节点相连.本文采用链接聚类系数与接近中心性来定义节点自身的吸引力：

图4 实例网络示意图Fig.4 Example network diagram

其中，Γ(i)表示节点i的邻居节点集合，m指节点i与节点j的共同邻居节点，ki指节点i的度值，指节点i的接近中心性.

为了使结构相似的节点间连接的概率更大，对两个节点的吸引力值作归一化处理，得：

将归一化处理的结果放入信息熵的计算公式中，最终得到已知节点间连边的权重Si，j：

1.3.2 融合属性偏好及预测偏差的计算

在政策网络中，节点间的连接关系与自身的属性有关.由于在整个网络中，部门属性的节点和主题属性的节点在已知连边中占比较高，容易与别的节点产生连接.为了使预测更准确，需要考虑节点自身的属性偏好，定义如下：

其中，counti，j表示节点i所代表属性与节点j所代表属性（如部门节点-主题节点存在连边）在网络中有连边的个数，sum 表示网络现有连边数，表示该权重矩阵的均值，counti，j/sum 表示属性的重要程度，Si，j/表示属性比值.

节点间的预测偏差值根据与网络节点中相似的节点来计算，Si'，j'表示与i节点最相似的节点和与j节点最相似的节点的边权值，预测偏差值为：

最终融合节点相似和属性偏好的多实体政策网络链路预测值为：

其中α和γ分别表示控制属性偏好和预测偏差的权重参数，α+γ=1，Ai和Aj表示潜在因子矩阵A的第i行和第j行.

2 实验结果和分析

2.1 实验配置

鉴于公开的政策网络数据集缺乏，本文构建了真实的多实体政策网络数据集.为确保数据的真实性与适用性，本文选择了2014—2021年期间的中央政府和6 个省政府发布的600 余篇关于农村创新创业的政策文本作为研究对象，并邀请专业人员对政策进行筛选鉴证.实验环境配置如表1所示.

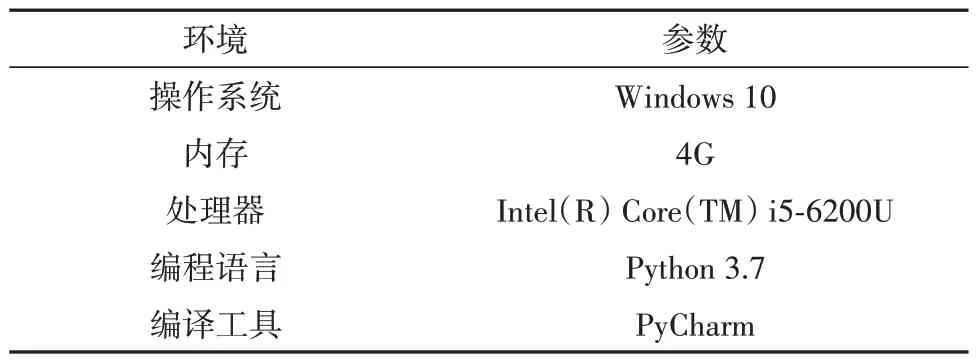
表1 实验环境Tab.1 Experimental environment

2.2 对比算法及评价指标

本文将改进的链接预测方法应用于构建的7个政策网络，以10种链路预测算法作为基准算法进行对比.为了验证本文提出的LP-NA 算法的效果，评价时使用链路预测中衡量准确度认可度较高的指标——AUC［13］.AUC 指标是根据测试集中边的相似值与不存在的边的相似值进行比较的，当测试集ET中边的相似值＞不存在边的相似值时，则加1 分；当测试集ET中边的相似值=不存在边的相似值时，则加0.5 分.假设经过独立比较n次，有n'次测试集ET中边的相似值＞不存在边的相似值、n''次测试集ET中边的相似值=不存在边的相似值.AUC 值越高表示此算法预测准确度越高.AUC定义如下：

2.3 多实体政策网络构建结果

根据政策数据集的数量，本文估计最佳主题数量在10～100 之间，通过计算模型在不同Z值下的困惑度选择最优的主题数量.困惑度随Z的变化如图5所示.

图5 不同Z值下困惑度的变化Fig.5 Variation of perplexity under different Z values

从图5 中可以看出，当Z的范围从10 到50 时，困惑度的值从大约1200 显著降低到450.尽管当Z＞50 时，困惑度仍在下降，但下降速度比之前要慢，因此，本文选定这600余项政策的主题数为50.由于篇幅原因，表2 展示所提取的部分主题.此外，本文提取了政策标题与发布部门，所提取的实体及其关系如表3所示.在上述工作中，本文提取了政策标题及其对应的发布部门，通过LDA 主题模型挖掘了政策标题与主题之间的关系，获得了构建多实体政策网络必要的三类实体及它们之间的关系.

表2 部分主题及关键词Tab.2 Part of the topics and keywords

表3 7个数据集中实体及关系的数量Tab.3 Number of entities and relationships in the seven datasets

中心性是网络理论中的一个基本度量指标，用于检测或识别网络中最具影响力的实体节点.为了评价政策网络的中心性，本文计算了7 个政策数据集中每个实体的接近中心性值和度中心性值［14］，并在表4中列出了最具影响力的实体节点及其中心性值.通过计算多实体政府政策网络的中心性，发现7 个数据集中最具影响力的实体几乎都是部门实体.例如，在中央数据集中，D41和D7是国务院及国务院办公厅.在四川省数据集中，T44 作为主题实体，包括了“创新创业”、“大学生创新”、“农产品加工”等关键词.在广西数据集中，D4 为自治区农村厅，D33为自治区人民政府.因为几乎每一篇政策标题实体都涉及到多个发布部门实体，且部门数量固定，因此部门实体在网络中最具影响力.

表4 7个政策数据集中心性最高值及对应节点Tab.4 Maximum values and corresponding nodes of centrality in seven policy datasets

为了找到各省对农村创新创业发展贡献最大的部门以及所涉及的热点话题，本文以湖北省政策网络为例，详细讨论实体节点，由于完整网络节点间关系庞杂，本文仅展示了政策标题、部门以及主题之间的关系，如图6所示.其中部分节点对应名称如表5 所示.由图6 中可见：实体节点D2（湖北省人民政府）与政策标题实体和主题实体的连接数量最多，这表明湖北省人民政府对湖北省农村创新创业的发展做出的贡献最大；另一方面，可以观察到湖北省各部门更加重视T25（农业科技创新农村电子商务）和T8（农村电子商务）主题.

表5 部分湖北省多实体政策网络节点对应名称Tab.5 Corresponding names of some Hubei multi-entity policy network nodes

图6 湖北省多实体政策网络Fig.6 Multi-entity policy network of Hubei Province

2.4 政策间潜在关系分析

表6 展示了在湖北省政策网络中，以湖北省委和湖北省人民政府于2019年联合发布的《湖北省乡村振兴战略规划（2018—2022 年）》为例的政策间相关性研究的结果，由于政策间的相关性预测值区间为［0-1］，因此相关性预测值以中间值0.5 为界限，预测值越高则表明这两篇政策越相关.根据表6 看出：《湖北省乡村振兴战略规划（2018—2022 年）》与2019 年湖北省旅游委、湖北省扶贫办联合发布的《关于支持深度贫困地区旅游扶贫行动方案》以及2020 年湖北省人民政府发布的《关于印发加快推进科技创新促进经济稳定增长若干措施的通知》《关于印发湖北省“擦亮小城镇”建设美丽城镇三年行动实施方案》相关性预测值分别达到0.651、0.614以及0.603，表明政策的有效实施.同时此链路预测结果可以根据预测值的大小为民众推荐相关的政策，实现民众与政策的精准对接，克服了政策分散在不同网站以及人工搜索方法获取政策不及时、不准确等问题，扩大了政策传播力度.而2020年发布的《关于加快推动水产养殖业绿色发展的意见》与《湖北省乡村振兴战略规划（2018—2022 年）》相关性预测值较低，为0.272，一方面可能因为在乡村振兴战略规划中，政策篇幅较多，涉及主题较广，是全局性的指导文件，其所涉及到的养殖领域涵盖畜牧、家禽、水产等不同的类型，而《关于加快推动水产养殖业绿色发展的意见》作为其水产养殖政策方面的细化，涉及领域比较单一，表明该政策与乡村振兴战略规划指导文件响应度不高，需加强湖北省农业农村厅、湖北省自然资源厅、湖北省财政厅等部门与湖北省人民政府在养殖领域的协同合作.

表6 政策间链路预测结果示例Tab.6 Example of inter-policy link prediction results

2.5 参数对算法性能的影响

为了证明LP-NA 算法对上述政策间链路预测结果的有效性，本文进行了分析对比.LP-NA 算法包含α、β和低秩维度K三个重要参数.在研究一个参数对AUC 值的影响时，需固定另外两个参数.本文分别做了10 组实验来确定α的值对LP-NA 算法性能的影响，确保取到可靠的参数.图7 为不同α值在不同数据集的AUC上的实验结果.由图7可见：随着参数α的增大，AUC值开始呈上升趋势，云南省和广西自治区政策网络数据集在α=0.4 时AUC 最大，中央、甘肃省以及河南省政策网络数据集在α=0.5 时AUC 达到最大值，而四川省和湖北省政策网络数据集则在α=0.6 时AUC 达到最大值.当α取值继续增加时，AUC 的值逐渐下降.当α值较小时，节点连边的属性偏好对AUC 的影响过小，而预测偏差值对AUC 的影响过大，此时预测值可能出现偏低的情况，使得预测误差增大；同理，当α值较大时也会导致预测值误差增大，导致AUC值降低.

图7 α值对误差的影响Fig.7 Impact of parameter α on the deviation

参数β是为了防止过拟合，其结果如图8 所示，可以看出中央、四川省以及甘肃省政策网络数据集在β=0.08 时达到最优效果，湖北省、云南省、广西自治区以及河南省在β=0.10时AUC 值达到最佳.由图8 可见：随着参数β的增加，各个数据集下的AUC 值呈现明显的先升后降的趋势，表明参数β对算法精度有较大影响.

图8 β值对误差的影响Fig.8 Impact of parameter β on the deviation

低秩维度K直接影响LP-NA 算法的性能，当K取值较大时，计算复杂度高；而当K取值较小时，其性能表现较差.图9表示7个数据集分别在各自α和β取最优值的前提下，低秩维度K的不同取值对AUC 值的影响.由图9 可见：各个数据集的AUC 值随着K值增加而逐渐增加，甘肃省、湖北省、云南省以及河南省政策网络数据集在K=30 时AUC 取得最大值，四川省政策网络数据集在K=35时AUC取得最大值，而中央和广西政策网络数据集在K=40 时AUC取得最大值.当AUC值增加到一个最值时，随着K值的继续增加，AUC 值趋于平缓，低秩维度K的增加对于AUC值的变化影响较小.

图9 K值对误差的影响Fig.9 Impact of parameter K on the deviation

为了测试LP-NA 算法的健壮性，本文分别测试了训练集占比由50%到90%时各种方法下的AUC值.以中央政策网络为例，实验结果如图10所示.由图10 可见：当测试集由50%增加到90%时，各个方法的AUC 值均有所上升，这是因为随着训练集所占比例的增大，节点间连边数增多导致链接聚类系数以及接近中心性值增大，节点间吸引力加强，使AUC 值上升.在不同的训练集规模下，LP-NA 的AUC 值都高于其他算法，表明本文提出的LP-NA 算法的健壮性优于其他算法.

图10 中央数据训练集从50%～90%时不同方法下AUC变化Fig.10 AUC changes under different methods when the central data training set varies from 50% to 90%

2.6 不同算法性能对比

表7 列出了政策网络训练集所占比例为90%时，7 个政策网络在不同算法下的预测精度AUC 值.由表7 可见：本文提出的LP-NA 算法与其他链路预测算法［15-23］相比，各个政策网络的预测精度AUC 值都取得了最大值.若与CN-L3算法进行比较，网络的预测精度AUC 值在中央政策网络中提高了4.76%，在四川省网络中提高了4.20%，在广西壮族自治区网络中提高了0.89%，在云南省网络中提高了3.08%，在甘肃省网络中提高了3.25%，在湖北省网络中提高了4.59%，在河南省网络中提高了3.03%.这是因为LP-NA 算法充分挖掘原始网络节点间的相似度且考虑了属性偏好及预测偏差，其他的算法仅考虑到共同邻居节点数、共同邻居节点度值以及聚类系数对预测的影响.因此可见：由于LP-NA 算法考虑了节点相似、属性偏好及预测偏差，获取信息相对丰富，使得预测精度有所提高.

表7 各算法对不同网络进行链路预测的AUC值Tab.7 AUC of each algorithm for link prediction of different networks

3 结语

本文通过预测政策网络中的尚未连边节点的连接概率，最大化地利用了政策信息为研究政策网络提供依据，也为民众提供了更方便快捷的政策信息服务.为了解决数据稀疏以及以往链路预测算法考虑不全面等问题，本文提出了一种融合节点相似和属性偏好的LP-NA 算法.LP-NA 融合节点相似和属性偏好去捕获局部和全局信息，通过矩阵分解，在求解过程中使用乘法规则进行参数学习，优化算法性能.在7 个多实体政策网络数据集上的实验结果表明，与现有算法相比，提出的LP-NA 算法能够有效提升链路的预测精度，挖掘出政策间的潜在关系，丰富了政策研究的方法，有利于促进部门间协同合作，为相关政策研究提供了参考.下一步的工作将研究有向政策网络的构建以及央地政策间的协同演进机制.