高效管换热器壳程传热强化效果及机理
吴志伟,王 通,王彦龙,赵克强,钱才富
(1.北京化工大学 机电工程学院,北京 100029;2.山东美陵化工设备股份有限公司,山东淄博 255000)
0 引言
管壳式换热器因其结构简单、成本低、适应性强等特点,广泛应用于石化、冶金、轻工、能源等领域[1-2],在换热设备中约占70%的市场份额,处于不可替代的主导地位。
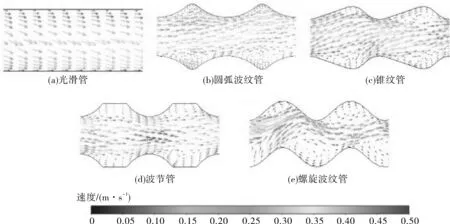
管壳式换热器的强化传热方式主要有管程强化传热和壳程强化传热。其中管程强化传热主要是通过改变换热管的形状,从而增强壁面处流体的湍动程度,如波纹管[3]、螺旋槽管[4]、缩放管[5]、波节管[6]等。关于高效管强化传热机理的研究一直是研究热点。KAREEM等[7]全面综述了波纹管管内流体流动和传热性能,包括层流和湍流,结果表明,波纹处会产生涡流,这是传热增强的主要原因,波纹节距和高度对工作流体的流动状态有显著影响,此外,由于螺旋波纹的存在,螺旋波纹管的传热性能进一步提高。CRCOLES等[8]通过数值模拟方法对螺旋槽管的波纹形状(定义波纹形状系数CSF)进行了深入研究,研究结果表明,在研究范围内(4 关于高效管强化传热的研究大多集中在管内传热,很少有针对高效管换热器的壳程强化传热机理的研究。本文建立4种管型的高效管换热器(圆弧波纹管、锥纹管、波节管和螺旋波纹管)壳程流体流动和传热数值模拟模型,研究高效管壳程传热强化效果和机理。 4种高效管换热器的几何模型如图1所示,具体尺寸参数见表1,换热管的排列方式见图2。 表1 换热器基本结构参数 图1 高效管换热器几何模型 图2 换热管排列方式 文中研究的高效管都是由光滑管(∅25 mm×2.5 mm)轧制而成,且具有相同的波纹深度和节距,其结构尺寸见图3,布管如图2所示。 L=18 mm,h=2.5 mm,R1=15 mm,R2=2.5 mm L=18 mm,h=2.5 mm,R1=5 mm,R2=6 mm L=18 mm,h=2.5 mm,R1=10 mm,l=7 mm L=18 mm,h=2.5 mm,α=77° 为简化数值模拟,作出以下假设:(1)壳程流体为不可压缩的牛顿型流体;(2)介质常物性稳态流动,重力的影响忽略不计;(3)换热管的外表面温度恒定。对于稳态条件,需满足流体动力学的基本控制方程——连续方程、动量方程和能量方程[12]。 雷诺数Re和普朗特数Pr: Re=ρuDe/μ (1) Pr=cpμ/ρ (2) 式中,ρ为流体密度;u为壳程流体流速;De为当量直径;μ为流体黏度;cp为流体比热容。 当换热管为正方形排列时,De计算表达式如下: (3) 式中,s为换热管间距;do均取基管外径。 传热计算理论公式如下: Q=qmcp(to-ti) (4) (5) (6) Δt1=tw-ti (7) Δt2=tw-to (8) Nu=hDe/λ (9) 式中,qm为质量流量;to,ti分别为热交换器的壳程出口温度和入口温度;S为热交换面积;Δtm为对数平均温差;tw为换热管壁面温度。 模拟时采用速度入口,且流体介质的入口温度设置为295 K。在换热管的壁面上设置350 K的恒定温度。壳程出口设置为压力出口,压力设置为0。忽略换热器表面的热损失,将其设为绝热。壳体内壁和计算域内的所有固体表面采用非滑移边界条件。为了简化模型,换热器采用1/2模型。数值模拟中使用的介质水的物理参数如表2所示。 表2 介质水的物性参数 在求解过程中,采用基于压力的隐式求解器,压力和速度采用 SIMPLEC 算法耦合,除压力外的所有变量均采用二阶迎风格式处理,激活能量方程。收敛准则的能量残差曲线标准为10-6,其余变量为10-4。计算湍流模型采用SSTk-ω。为验证数值计算准确性,建立了相同结构参数的光滑管换热器模型,并分别将采用SSTk-ω和Realizeblek-ε为湍流模型的换热器数值模拟结果与换热器壳程努塞尔数经验公式[12](式(10))计算对比,结果如图4所示。在研究范围内采用SSTk-ω计算结果与经验公式更为接近,最大偏差在5.5%,故本文采用SSTk-ω湍流模型。 图4 数值计算验证 Nu=0.36Re0.55Pr1/3(μ/μw)0.14 (10) 以波纹管换热器为例,其整体采用非结构化网格划分,并对局部区域进行网格加密,如图5所示,表3示出网格无关性考核结果。可以看出,当网格数量从16 623 087增加到27 094 008时,壳程努塞尔数和压力降的相对误差均在3%以内,认为满足了网格无关性的要求。文中其他高效管换热器采用相同的网格尺寸。 表3 网格无关性计算结果 图5 圆弧波纹管换热器网格模型示意 图6示出各换热器壳程努塞尔数随雷诺数的变化。可以看出,与光滑管相比,4种高效管的壳程传热性能有了明显提高。雷诺数在7 392~36 960的范围内,圆弧波纹管、锥纹管、波节管、螺旋波纹管的壳程努塞尔数分别比光滑管提高了11.01%~28.74%,9.55%~25.13%,7.52%~24.75%,26.2%~46.78%。其中强化效果小的对应于较大的雷诺数,例如,对于圆弧波纹管、锥纹管、波节管换热器来说,壳程雷诺数为36 960时,高效管的壳程努塞尔数仅比光滑管提高约10%。这是由于雷诺数的提高,光滑管换热器的壳程流体湍流程度也提高了,使得光滑管和高效管换热器壳程之间的流动状态差异变得不显著,高效管的传热强化效果自然也就减小了。 图6 各换热器壳程努塞尔数Nu随雷诺数Re 图7示出各换热器壳程压降随雷诺数的变化。可以看出,随着壳程雷诺数的增加,换热器壳程压降迅速增加。整体来看,换热器管型的不同对壳程压降影响不大;而有些意外的是,与光滑管相比,圆弧波纹管、锥纹管、波节管的壳程压降分别下降了3.42%~7.9%,5.98%~9.14%,8.79%~9.81%,这是由于圆弧波纹管、锥纹管、波节管的管径周期性收缩,使得壳程流通面积略有增加造成的。对于螺旋波纹管,壳程流通面积相对光滑管没有增加,而螺旋结构加大了管壁附近流体的湍流程度,因此,螺旋波纹管的壳程压降增加了0.22%~4.98%。 图7 换热器壳程压降ΔP随雷诺数Re变化的关系曲线 Nu/ΔP用于表示换热器的综合传热性能。图8示出高效管换热器壳侧Nu/ΔP与光滑管换热器管壳侧Nu/ΔP的比值,纵坐标值均大于1,这表明在综合考虑传热和流动阻力时,圆弧波纹管、锥纹管、波节管、螺旋波纹管的壳程综合性能均优于光滑管换热器,其中螺旋波纹管的壳程综合传热性能最强。 图8 高效管与光滑管换热器壳程Nu/ΔP之比与Re的关系 管壳式换热器的壳程流体在折流板的引导下呈“Z”形流动,流体流动方向和管子轴向之间的夹角不断变化,若将沿管子和垂直于管子的流动分别称为纵向流和横向流,则在折流板弓形缺口区域的管子周围的流体流动主要为纵向流,而在非缺口区域管子周围的流体流动主要为横向流,对于有波纹外形的高效管,对纵向流和横向流的传热强化效果应该有所不同,以下从不同角度进行研究,以探讨高效管壳程传热强化机理。 首先考察波纹对壳程横流传热性能的影响,为此,建立在折流板缺口区域未布管的光滑管和圆弧波纹管换热器有限元模型,以排除缺口区域纵流的传热,如图9所示。此时换热器有限元模型除了换热管数目不同外,其余结构参数均与前文保持一致。 图9 折流板缺口区域未布管换热器结构示意 当壳程雷诺数为11 088时,折流板缺口区域未布管时和缺口布管时换热器的计算结果分析如表4所示。折流板缺口布管时,圆弧波纹管换热器的壳程努塞尔数比光滑管管壳式换热器提高了28.7%,而在折流板缺口区域未布管的圆弧波纹管和光滑管换热器壳程努塞尔数仅相差3.25%。 表4 折流板缺口区域是否布管对传热性能的影响 为进一步证实高效管在折流板缺口区域传热性能的提高,还模拟了只在缺口区域布直管的圆弧波纹管换热器传热性能,并和在缺口区域不布管和布波纹管的换热器相比较,结果见表5。 表5 折流板缺口区域换热管对圆弧波纹管换热器传热性能的影响 从表5可以看出,和缺口区域布波纹管相比,缺口区域不布管的换热器壳程Nu下降了7.27%,而缺口区域布直管的换热器壳程Nu却降低了25.22%。比较表4和表5可以发现,缺口区域布直管的波纹管换热器和光滑管换热器壳程Nu很接近,前者壳程Nu为106.4,而后者壳程Nu为110.54,这也再次证明了缺口区域不布管的波纹管换热器没有明显传热强化作用。 因此,可以认为对于纵流,波纹结构可以有效提高壳程传热性能;而对于横流,波纹结构没有明显提升壳程传热性能。 由同种管型换热器对比发现,折流板缺口区域未布管的波纹管相对于缺口区域布管换热器壳程Nu有所下降,而光滑管换热器壳程Nu却有所提升。这是由于光滑管管壳式换热器在非缺口区域的横流换热性能好于折流板缺口部位的纵流换热性能;而波纹管换热器则相反,波纹管在缺口区域纵流传热性能好于不在缺口区域的纵流传热性能,这点还可从下文两折流板中间位置和折流板缺口部位的局部平均传热系数得到佐证。 所以,对于高效管换热器,折流板缺口区域布管可以提升整个换热器传热性能;而对于光滑管换热器,折流板缺口区域布管则拉低了整个换热器传热性能。不过应该说明的是,折流板缺口区域是否布置换热管会影响传热性能,但由于总的换热面积改变了,对换热器传热能力的影响应该是不一致的。 为进一步考察横流管束的壳程传热性能,提取壳程Re为11 088时各换热器在非缺口区域沿管长的局部传热系数并进行对比,结果见图10。 图10 折流板非缺口区域沿管长局部传热系数 从图10可以看出,由于折流板背风侧流动死区的存在,各换热器壳程流体在折流板迎风侧局部传热系数均有所提高,即从左到右,局部传热系数整体有所提高。对高效管换热器在图示范围沿管长方向的局部传热系数取平均值,结果见表6。 表6 壳程非缺口区域沿管长局部传热系数 从表6可以看出,高效管换热器的局部平均传热系数和光滑管换热器比较接近,相对偏差在4%之内,再次说明由于主要为横流,在管壳式换热器非缺口区域,高效管传热性能相比于光滑管并没有提高。 在管壳式换热器中,折流板缺口区域的流体呈纵向流趋势,流体流动状态受到管型结构的影响。 在缺口区域,换热器壳程流体主要为纵向流,速度矢量图如图11所示。可以看出,光滑管换热器的壳程流体主要为直线顺流,而对高效管换热器,由于管壁具有波纹结构,对壳程流体流动造成较强的扰动,甚至在波纹波谷处还形成了局部涡流,增强壁面流体的湍流程度。螺旋波纹管管间流体湍流程度最为剧烈,这是因为其管间流体是在三维空间周期性旋转的,流体遇到螺旋形的管壁会产生偏离主流方向的二次流,会在流道产生大范围旋流。 图11 折流板缺口区域壳程流体速度云图 图12示出壳程Re为11 088时,折流板缺口区域管子沿管长方向的壳程局部传热系数。 图12 折流板缺口区域沿管长局部传热系数 由图12可看出,圆弧波纹管、锥纹管、波节管换热器的局部换热系数随着波纹波谷波峰的位置而变化,这是由于在波谷附近(即在壳程流域的开阔处)壳程流体湍流程度较高,其附近管壁局部传热系数相对波峰处较大,这与管内流体在波峰处局部传热系数最大有着相同的表现[13-18]。光滑管和螺旋波纹管在此处的局部传热系数波动较小,这是因为两种管横截面积保持不变,沿管长方向,管间壳程流体流动速度变化不大。 同样,计算折流板缺口区域壳程流体局部位置的传热系数,如表7所示。可以看出,圆弧波纹管、锥纹管、波节管、螺旋波纹管的局部传热系数均比光滑管有明显提高,螺旋波纹管提高尤为显著。 表7 壳程折流板缺口区域沿管长局部传热系数 综上所述,从壳程流体局部区域的传热系数可以看出,高效管在以纵流为主折流板缺口区域的传热性能高于在以横流为主的非折流板缺口区域的传热性能,而这也是高效管换热器壳程传热性能要高于光滑管换热器的主要原因。 (1)在所研究的雷诺数范围内,高效管换热器壳程换热性能均比传统光滑管换热器有明显提升,圆弧波纹管、锥纹管、波节管、螺旋波纹管换热器的壳程努塞尔数相比传统管壳式换热器分别提高了11.01%~28.74%,9.55%~25.13%,7.52%~24.75%,26.2%~46.72%。 (2)与光滑管相比,螺旋波纹管的壳程压降增加了0.22%~4.98%,但圆弧波纹管、锥纹管、波节管的壳程压力降分别降低了3.42%~7.9%,5.98%~9.14%,8.79%~9.81%。高效管换热器壳程综合传热性能均比光滑管有所提高,其中螺旋波纹管换热器的壳程综合传热性能最强。 (3)对于高效管换热器,折流板缺口区域布管会提升整个换热器的传热性能,而对于光滑管换热器,折流板缺口区域布管会降低整个换热器的传热性能。 (4)折流板缺口区域高效管的壳程传热性能高于非缺口区域高效管,而折流板缺口区域光滑的管壳程传热性能低于非缺口区域光滑管。 (5)对于文中研究的换热器,折流板缺口区域高效管的壳程局部传热系数明显高于光滑管,高出值在23%~51%之间。而折流板非缺口区域高效管的壳程局部传热系数和光滑管接近,相对差值在4%以内。 (6)高效管在以纵流为主的折流板缺口区域的传热性能高于在以横流为主的非折流板缺口区域的传热性能,这是高效管换热器壳程传热性能要高于光滑管换热器的主要原因。1 有限元分析模型
1.1 几何模型

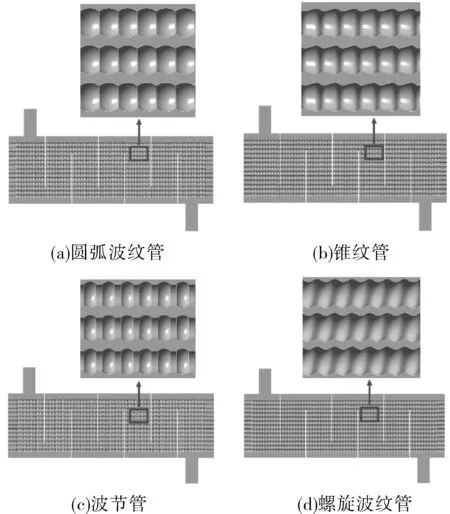
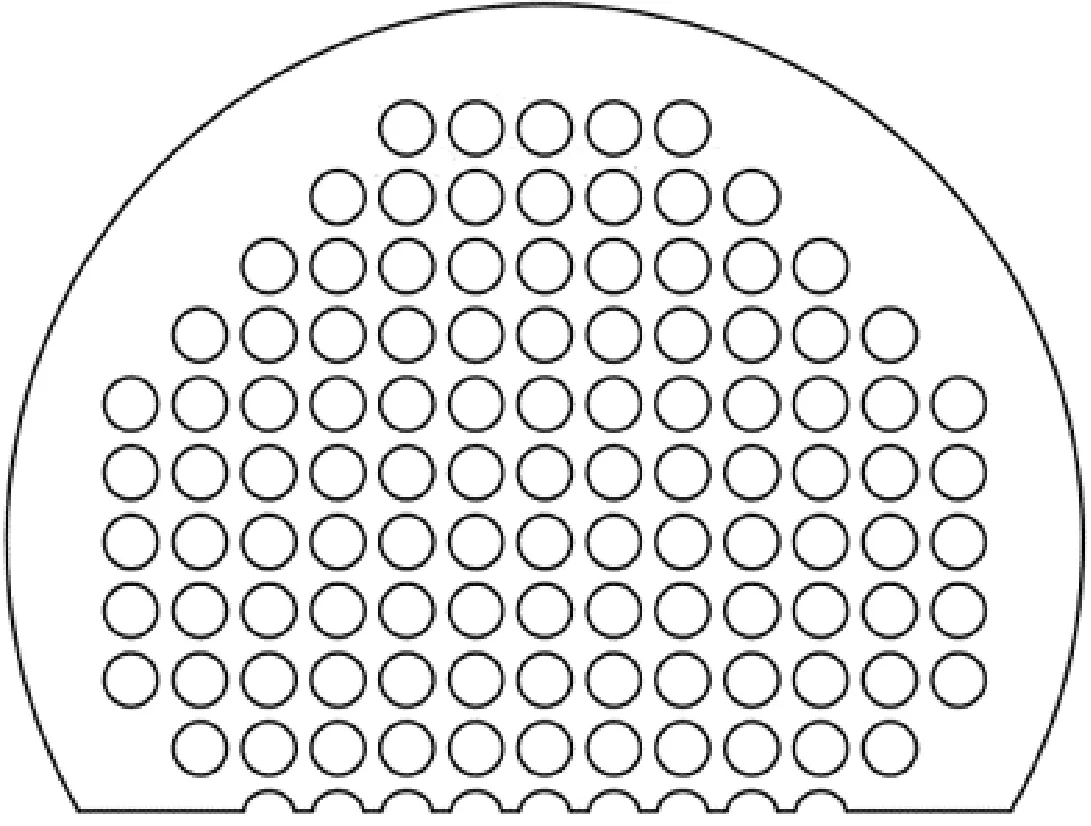
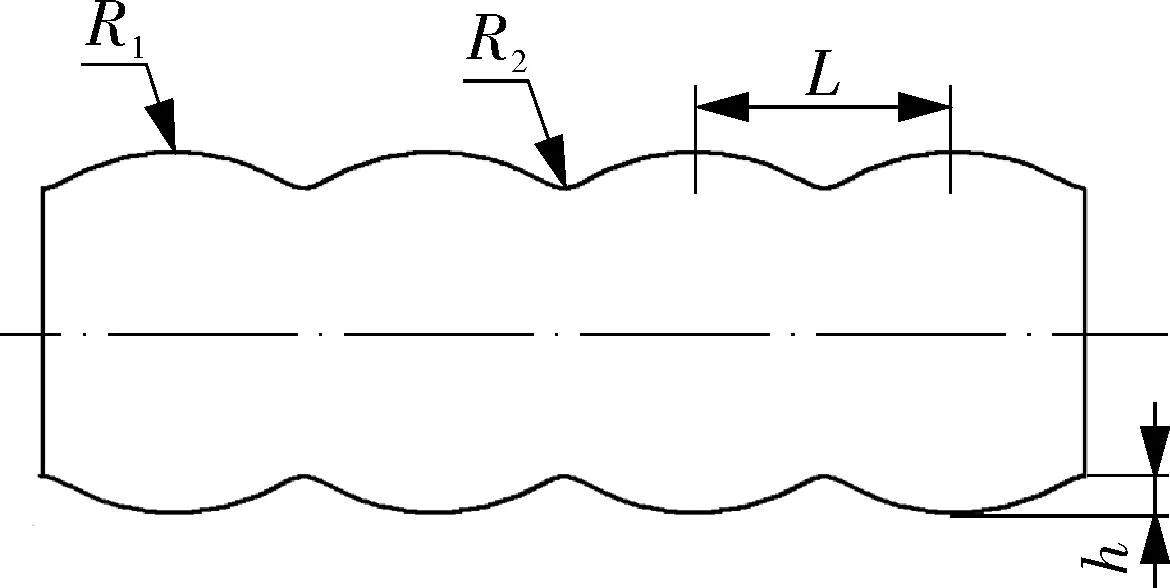
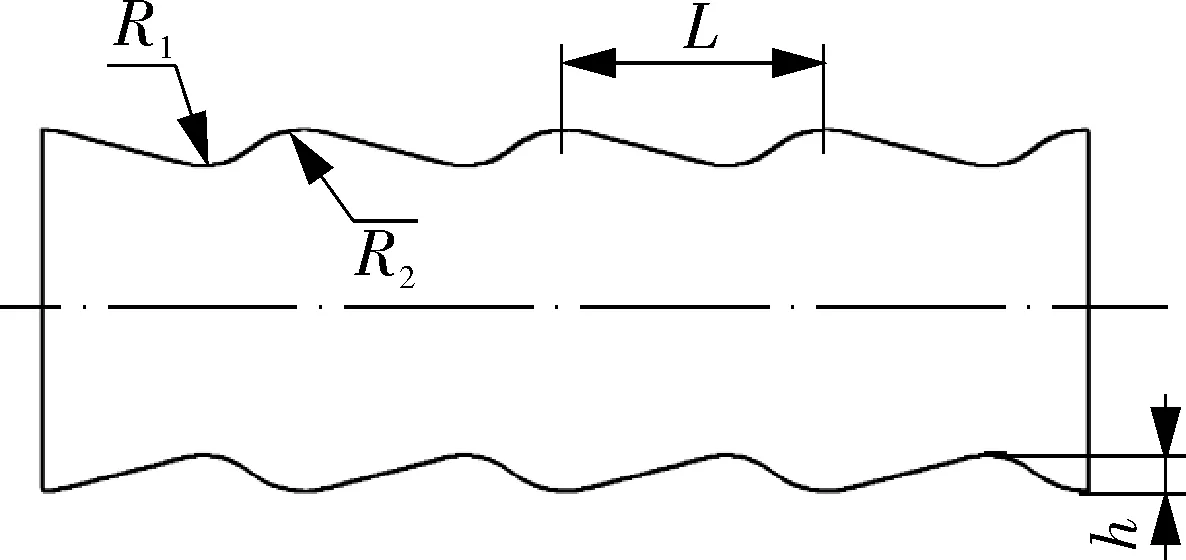
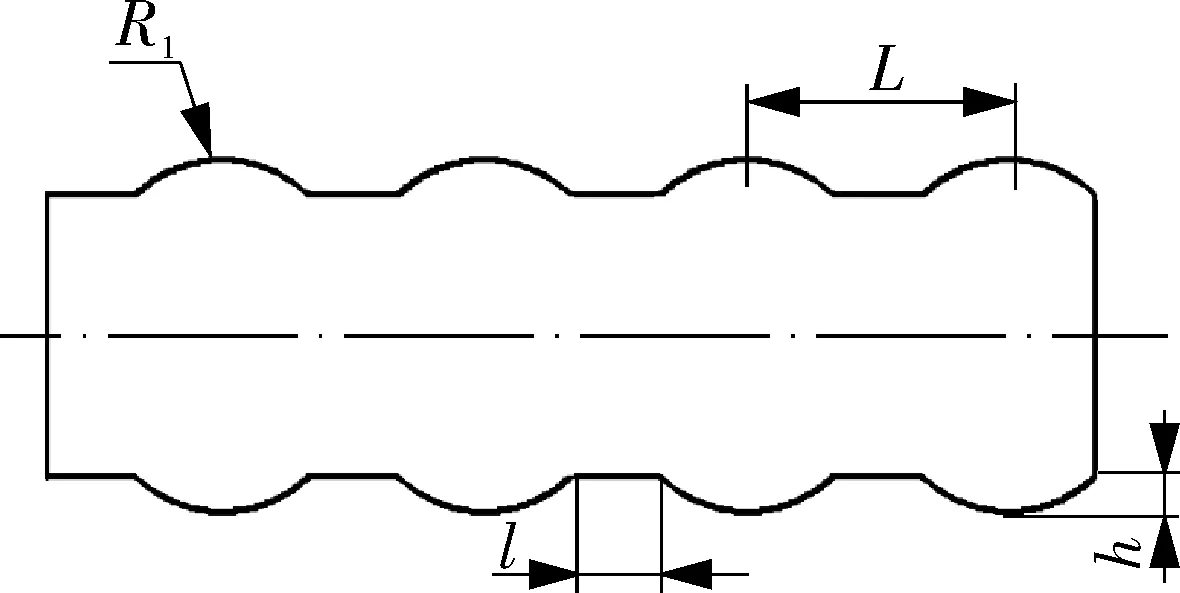
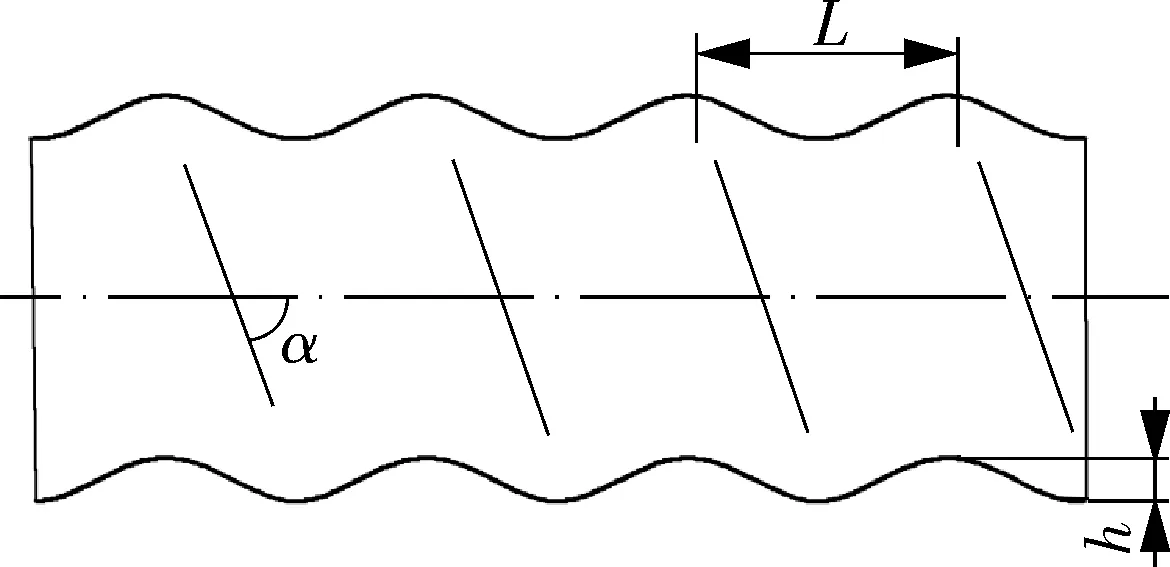
1.2 控制方程
1.3 流动和传热参数计算
1.4 边界条件和湍流模型

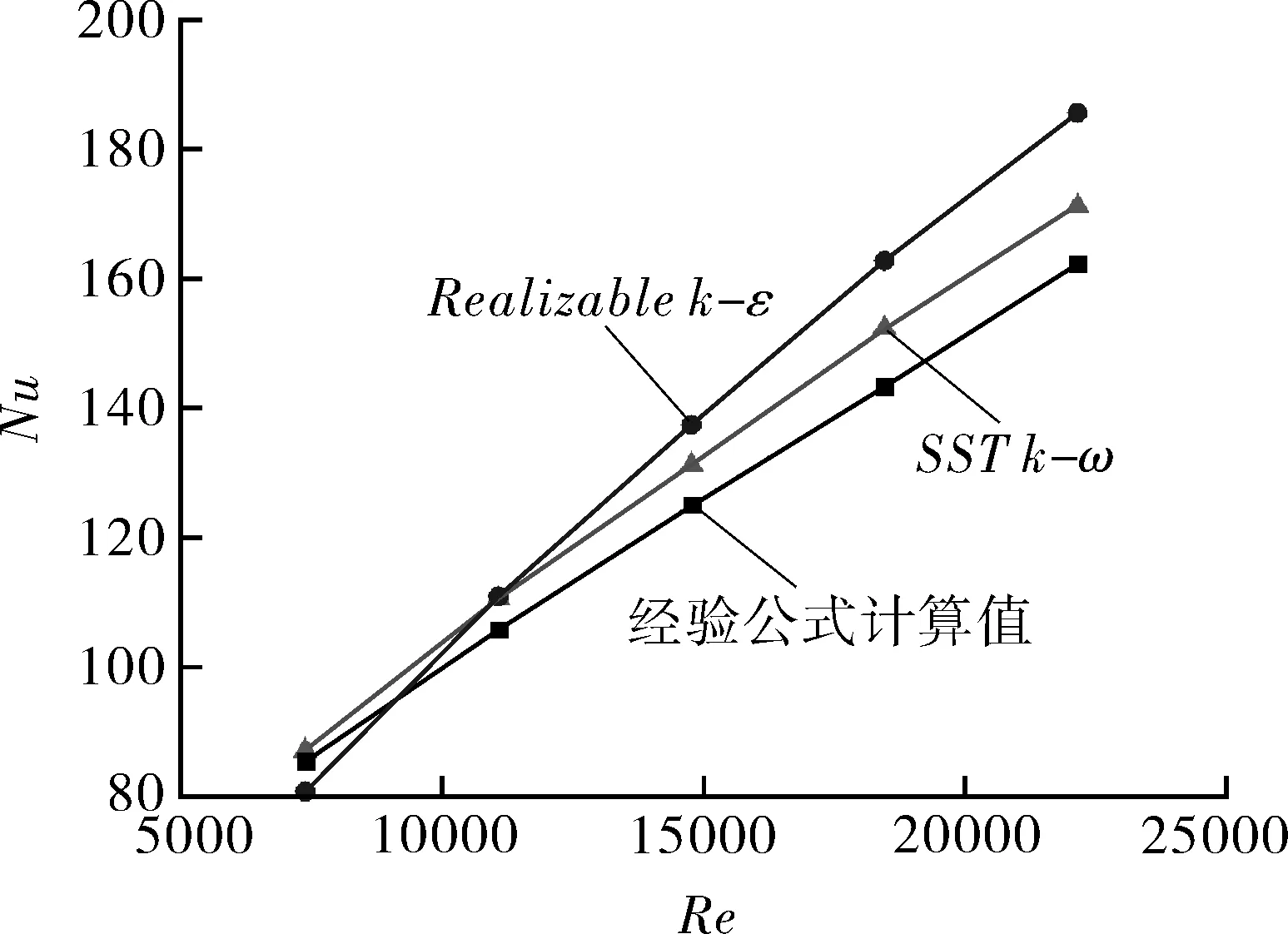
1.5 网格划分和无关性验证


2 高效管壳程传热强化效果


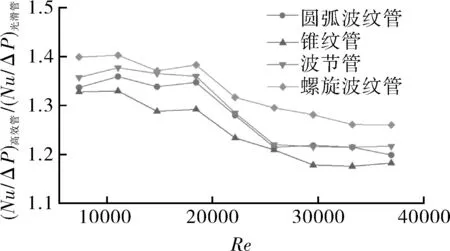
3 换热器壳程强化机理
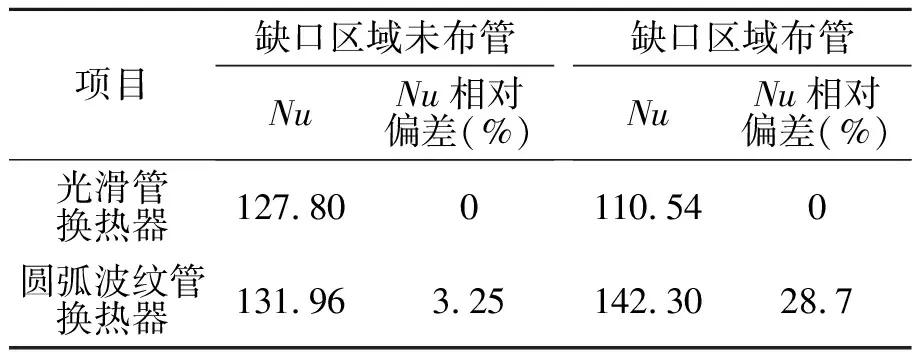
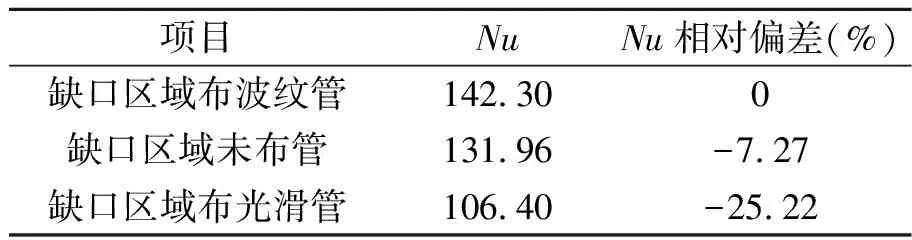
3.1 缺口布管对壳程努赛尔数的影响
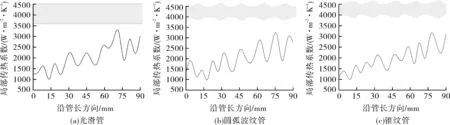
3.2 非缺口区域管子局部传热系数分析
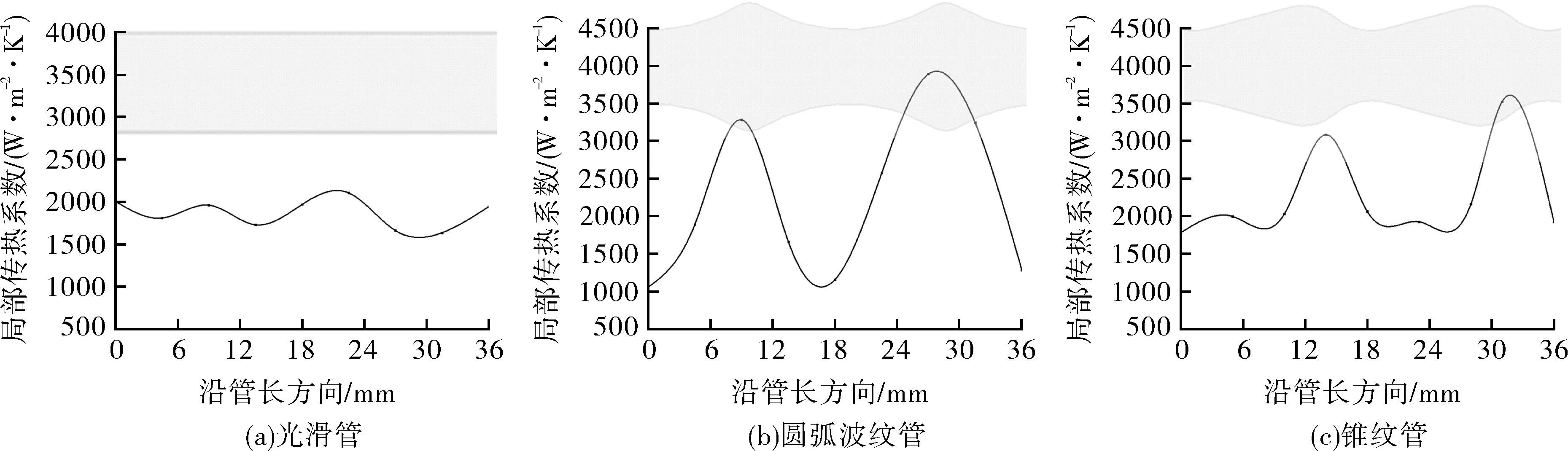

3.3 缺口区域管子局部传热系数分析

4 结论

