非齐次线性方程组解的一点注记

董 珺,魏 杰

(兰州工业学院 基础学科部,甘肃 兰州 730050)

设有线性方程组

(1)

式中:系数aij和常数项bi都是已知实数,i=1,2,…,m;j=1,2,…,n,x1,x2,…,xn是未知元。

当b1=b2=…=bm=0时称式(1)为齐次线性方程组,否则称式(1)为非齐次线性方程组。式(1)的系数矩阵A,增广矩阵(A,b)分别为

方程组(1)的矩阵形式为Ax=b,其中

传统的线性代数教材[1]在求解线性方程组时,首先判断增广矩阵的秩是否等于系数矩阵的秩,若不相等,则方程组(1)为矛盾方程,此时线性方程组无解;若相等,则需利用线性方程组的同解变形等方法求出原线性方程组的一个特解和对应的齐次线性方程组的基础解系,进而得到通解。其中求特解和基础解系是分步进行的,过程较为冗长,从而减少了学生学习的兴趣,增加了解题难度,影响了解题效率。

为此,许多专家学者不断尝试给出线性方程组更为简便的求解方法,已有一些结果[2-3]。

本文中所讨论的矩阵A均指m×n矩阵,x均指n维列向量,R(A)表示A的秩,所讨论的非齐次线性方程组Ax=b均指有解方程组。

1 线性方程组的简便解法

文献[2]中,乔虎生等证明了:对m×n矩阵A只通过有限次初等行变换得到的矩阵B中,一定存在一个r阶的单位子矩阵。据此给出了一种求解齐次线性方程组Ax=0的简便解法:

假设选取r阶单位子矩阵E时选取了矩阵B的t1,t2,…,tr列,则其余列对应的未知元即为自由未知量。让这些自由未知量“轮流”等于1,剩下的未知量等于0,然后把取1的列的非零元的相反数“依次”填入其余位置,即得原方程组的基础解系。

此方法虽然避免了最后还要通过未知数的代换才能求出基础解系的复杂过程,但是如何将矩阵A恰好化为矩阵B并不好把握,而由文献[1],将A很容易能化为行最简形矩阵。

基于此,结合初等行变换得到的方程组与原方程组同解,可将此简便解法改进为:

方法1首先对系数矩阵A进行有限次初等行变换得到行最简形矩阵B,则B的非零行个数即为A的秩。设A的秩R(A)为r,并假设B的非零行的非零首元素所在列为t1,t2,…,tr列,则其余n-R(A)列对应的未知元即为自由未知量。让这些自由未知量“轮流”等于1,剩下的未知量等于0,然后把取1的列的非零元的相反数“依次”填入其余位置,即得原方程组的基础解系。

例1求齐次线性方程组

的通解。

解对系数矩阵A实施初等行变换化为行最简形矩阵

则R(A)=R(B)=2。故方程组的基础解系中含有4-R(A)=2个解向量,从而方程组的通解为x=k1η1+k2η2的形式,其中k1,k2为任意常数,η1,η2为4维列向量。

由于非零首元素位于矩阵B的1,3列,故剩下的2,4列对应的未知元x2,x4为自由未知量。

由方法1,首先取η1,η2中的第2和第4个分量为1,0和0,1,然后把矩阵B中2,4列的第1和第2个分量对应的数字变号填入η1,η2中的第1和第3个分量,得

η1=(1,1,0,0)T,η2=(1,0,2,1)T,

即为原方程组的一个基础解系。因此,方程组的通解为x=k1η1+k2η2,其中k1,k2为任意常数。

注此方法只需对系数矩阵实施初等行变换化为行最简形矩阵,然后就可直接写出通解,有效减少了计算过程,从而提升了解题效率。

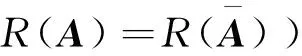
例2求方程组

的通解。

由于非零首元素位于矩阵C的1,2列,故剩下的3,4,5列对应的未知元x3,x4,x5为自由未知量。

由方法2,首先取η1,η2,η3中的第3、第4和第5个分量为1,0,0、0,1,0和0,0,1,同时让β中第3、第4和第5个分量都等于0; 然后把矩阵C中3,4,5列的第1和第2个分量对应的数字变号填入η1,η2,η3中的第1和第2个分量,同时让β中的第1和第2个分量等于d的第1和第2个分量,得

η1=(-2,1,1,0,0)T,η2=(-2,1,0,1,0)T,

η3=(-6,5,0,0,1)T,β=(6,-4,0,0,0)T,

即得所求方程组的通解x=k1η1+k2η2+k3η3+β,其中k1,k2,k3为任意常数。

方法2还可推广到解矩阵方程组AX=B的情形,其中A为m×n矩阵,X为n×s矩阵,B为m×s矩阵。

例3求解矩阵方程组AX=B,其中

解对方程组AX=B的增广矩阵实施初等行变换

则R(A|B)=R(A)=2,方程组有无穷多解,且其导出组的基础解系含有3-R(A)=1个解向量。

记X=(x,y),A=(β1,β2),则AX=B可写为两个方程组Ax=β1,Ay=β2。由方法2,用例2同样的取法,可分别得到这2个方程组的通解为

x=k1(0,-1,1)T+(1,-1,0)T=(1,-k1-1,k1)T,

y=k2(0,-1,1)T+(0,-1,0)T=(0,-k2-1,k2)T.

2 结论

1) 本文给出了求解线性方程组的一种新解法,用这种方法求齐次线性方程组或求非齐次线性方程组的通解时,只需对系数矩阵或增广矩阵实施初等行变换化为行最简形矩阵即可。

2) 与经典方法相比(见文献[1]),省掉了写矩阵对应的方程组,以及设自由未知量等繁杂过程,简单而实用,且易于掌握。

3) 与文献[2]的方法相比,有效避免了如何将矩阵恰好化为存在一个r阶单位子矩阵的矩阵的难题。

4) 与文献[3]的方法相比,所用符号表示与国内现行大多数教材一致,用起来更为方便,且不会出现在求解非齐次线性方程组的方法中,有限制地使用列、行初等变换,容易混淆,易导致错误发生等问题。