基于CSM的含DG配电网自适应过电流保护优化整定计算

黄 磊,李 梅

(安徽理工大学 电气与信息工程学院,安徽 淮南 232000)

随着新能源技术的成熟,大量分布式电源(Distributed Generator, DG)并入配电网,这将导致原有的保护整定方法在应用于含DG的有源配电网时存在一定的局限性[1-3]。

目前主流的研究方法是建立定值优化问题对应的数学模型,选取合适的优化算法对保护定值进行整定计算的方式[4-6]。在建立数学模型时,将各保护的动作时间之和的最小值作为目标函数,忽略了线路中主备保护之间存在的时间级差,不符合电力系统实际的运行情况[7-9]。文献[10-12]中选择了固定2个动作特性系数来优化求解继电保护装置中的时间整定系数和启动电流整定系数的方法,匹配动作时间和短路电流值。而随着数字继电保护装置的发展,产生了新的优化整定方法。在文献[13]中第一次提到了将动作特性系数作为连续变量来探究整定优化的最佳方案,文中列出了真值表,通过分析确定了当前系统的最佳方案,但是并未考虑这种方案对含DG的系统的适用性。

针对上述的研究现状,本文提出了一种基于CSM的自适应过电流保护定值优化方案。在该方案中选取了考虑主备保护同时最小化的数学模型,通过遗传算法混合非线性规划函数进行优化整定计算,并引入了自定义选择模块(Custom Selection Module, CSM)来确定每个系统的最优整定方案。在Matlab中搭建不同的系统,仿真结果验证了本文提出方法的有效性。

1 优化整定计算数学模型

1.1 保护动作特性方程

传统的保护动作特性方程为

(1)

式中:t为系统中各个继电保护装置的动作时间;TDS为时间整定系数;If为短路电流值;α和β为动作特性系数,常规的系数取值见表1;Iop为启动电流值,当短路电流大于此值时,保护动作。

表1 动作特性系数

启动电流整定系数Ip为

(2)

式中:CTR为保护的电流互感器变比。

文献[1]与文献[4]在取值时都参考了标准特性(SI),通过最小化整体动作时间来优化时间整定系数(TDS)和启动电流值(Iop)这2个系数,进而得到各保护的最优整定值。本文提出了自定义选择模块(CSM),将动作特性系数(α和β)视为连续变量,加入了上下界,通过分析不同情况下的优化整定值来选取系统的最佳方案。

1.2 待优化目标函数

当保护系统在自适应模式下工作时,必须计算过电流保护的最优整定值。它通常被表述为一个含约束条件的非线性优化问题。文献中最常用的目标函数是使所有过电流保护装置的运行时间之和在最大故障电流下最小,该目标函数表示为

(3)

式中:m为区域内保护设备的个数;ti为第i个继电保护装置的动作时间,计算如式(1)。

实际上,目标函数式(3)仅使一次保护的工作电流最小,而不考虑后备保护的工作时间。为了使主保护与后备保护的动作时间同时最小化,提出了一种考虑主备保护同时最小化的目标函数,即

(4)

式中:tp,i、tb,j分别为主保护和后备保护的运行时间;MCT为主备保护之间的时间级差,本文取0.2 s[1]。

主备保护对的主保护和相应后备保护的动作时间之间的协调时间间隔(CTI)定义为

CTI=tb-tp.

(5)

如果主保护和相应的后备保护的动作时间之间的时间级差大于预先指定的MCT,则称主备保护对正确动作。

1.3 约束条件

1) 对于任意线路k处的故障,动作时间的约束条件为

tmin≤ti≤tmax,

(6)

tb,j-tp,i≥MCT,

(7)

式中:tmin、tmax分别为动作时间ti的最大值和最小值。

2) 时间整定系数TDS和启动电流Iop应该在允许范围内,即

TDSi,min≤TDSi≤TDSi,max

(8)

Iop,i,min≤Iop,i≤Iop,i,max

(9)

式中:TDSi,min、TDSi,max分别是时间整定系数TDSi的最小和最大值,本研究分别取值为TDSi,min=0.1,TDSi,max=1.1;Iop,i,min、Iop,i,max分别是启动电流的最小和最大值,通常情况下要大于流过各线路的最大负荷电流,而且应该小于线路故障时流过保护的最小短路电流值[7]。

2 基于CSM的动作特性分析

2.1 特性分析

目前采用的数字过电流继电保护具有可以允许用户自适应特性曲线的优点,能够显著地提高继电保护的灵敏性和速动性,用户可以通过改变动作特性方程中的系数来选择自己需要的保护特性。数字继电保护中,动作特性系数分别为时间整定系数(TDS)、启动电流整定值(Ip)、动作特性系数(α和β),通过动作时间特性方程(1)可知,系数TDS和α具有直接的相互影响,两者同时最小在数学上是不合乎逻辑的。假设系数α最小,为0.14,将其乘以系数TDS的最大值1.1,其结果等于0.154,如果将系数α最大值80乘以系数TDS的最小值0.1,结果等于8。因此由动作时间特性方程(1)可知,在CSM中将时间整定系数TDS选择为固定最小值,将系数α作为整定值能够很明显地减小继电保护装置的动作时间。

在分析中发现,系数Ip与α分别增大都会使动作时间增大,而系数β增大时,会使动作时间值减小,因此在优化过程中系数β不能缺少。启动电流整定值Ip的上下界是由流过各线路的负荷电流以及线路故障时流过保护装置的最小短路电流确定的,虽然为选择值,但是如果在优化整定计算中固定Ip求解其他整定值,得出的目标函数以及各整定值很难满足实际系统的要求。而通常只优化一个系数很难得到最优的整定值,因此在系统发生故障时,CSM会在如表2所示的2种方案中选择最佳方案并计算整定值。

表2 CSM系数真值

2.2 方案流程

在该方案中,首先通过检测发生故障与否来确定该模块是否工作,当系统发生故障时,CSM会收集系统中各保护的故障电流,通过对比计算得到系统最佳的整定值优化计算方案以及该系统的保护最优整定值,接着保存该状态作为系统的全程保护。基于CSM的方案流程见图1。

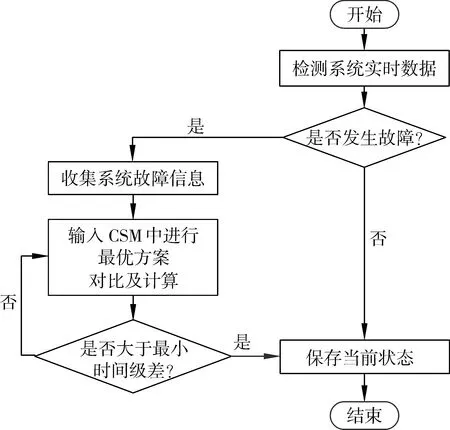
图1 基于CSM的方案流程

3 算法选择

3.1 非线性规划模型

(10)

式中:x、b、beq、lb和ub是矢量;A和Aeq为矩阵;c(x)和ceq(x)为返回矢量的函数,c(x)为不等式约束,ceq(x)为等式约束;f(x)、c(x)和ceq(x)是非线性函数。

配电网自适应过电流保护整定值优化计算数学模型其实就是一种非线性规划数学模型。在式(10)中,minf(x)即为整定值优化计算的目标函数,将动作特性方程中的系数以及动作时间的上下界融入到非线性规划模型中,即可进行整定值优化计算。

3.2 算法融合

非线性规划函数具有很强的局部搜索能力,但是全局搜索能力较弱,而遗传算法搜索时通过选择、交叉、变异步骤,全局搜索能力很强,但是局部搜索能力较弱,求解的最终结果一般为次优解而不是要最优解。所以本文通过混合遗传算法与非线性规划函数(fmincon)来计算问题的全局最优解。具体的流程如图2所示。

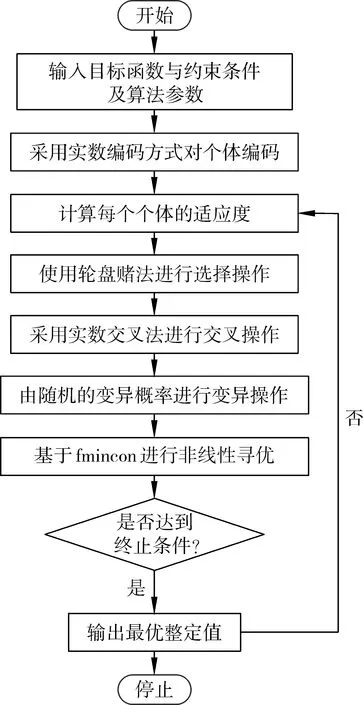
图2 算法流程

4 仿真及结果分析

本文为研究CSM模块在不同系统中进行最优方案对比计算的有效性,本文选择了含DG的4节点环网测试系统和IEEE15节点测试系统2个算例。在研究中不仅分析了CSM中的2种方案,还加入了标准动作时间特性分析 (后文中统一为方案3)作为对比。

4.1 算例1

首先在仿真软件Matlab中构建了含DG的4节点环网测试系统,如图3所示。该系统中包含2个分布式电源DG1和DG2,4条母线,4条输电线路以及8个继电保护装置,编号分别为1～8,故障位置选择在4条输电线路的中间位置,故障类型为最严重的三相短路故障。

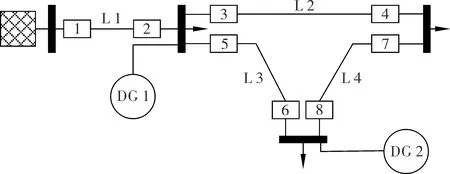
图3 4节点测试系统

当系统发生故障后,各个继电保护装置处经测量得到的故障电流如表3所示,每个继电保护装置在作为本线路主保护的同时还会作为其他线路的后备保护。

在得到各个保护位置的故障电流后,通过目标函数式(4)分别计算方案3以及CSM中的2种方案的目标函数值作为对比,结果如表4所示。

表4 4节点测试系统目标函数值

从表4中可以看到,CSM中2种方案的目标函数值相比较于方案3小很多,因此CSM在目标函数值最小化方面有很明显的优势,相对比方案1,方案2的目标函数值更小。图4～5表明CSM中的2种方案都满足系统快速切除故障的要求,即大于最小时间级差。因此CSM 会选择方案2作为最佳方案来进行整定值优化计算。采取方案2得到的最优整定值如表5所示。

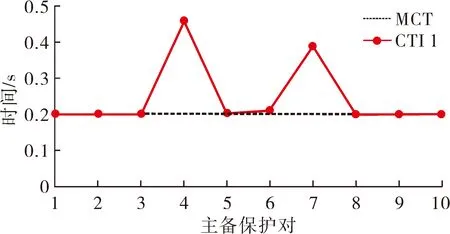
图4 方案1时间级差对比

图5 方案2时间级差对比

表5 4节点测试系统最优整定值

4.2 算例2

接下来选取如图6所示含DG的IEEE15节点测试系统来进行分析,系统中共包含7个DG,42个继电保护装置,分别编号1～42。当系统发生故障时,各个继电保护装置处的故障电流如表6所示。

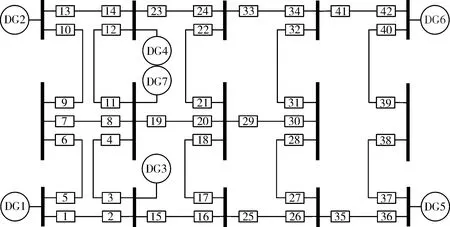
图6 IEEE15节点测试系统

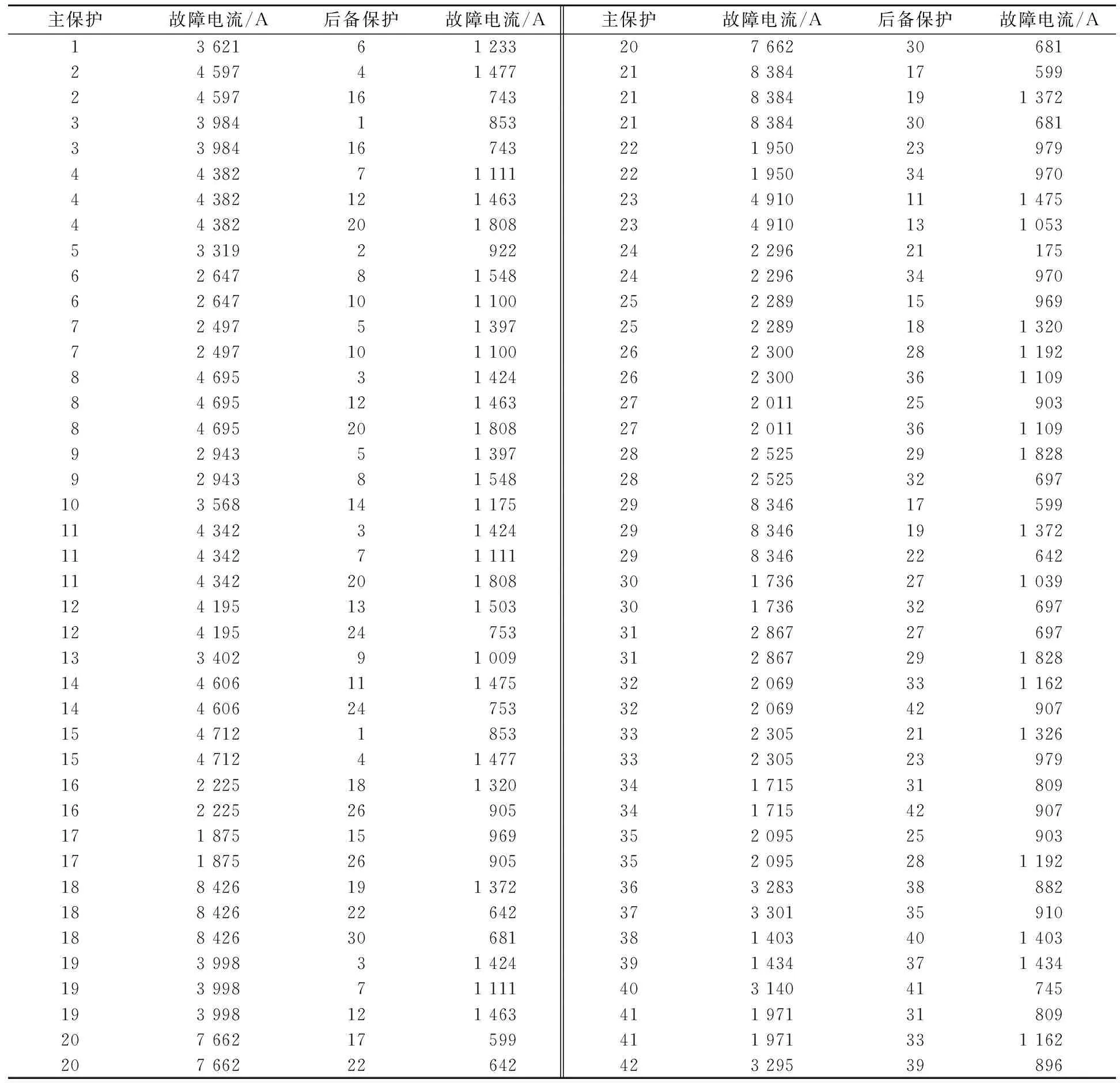
表6 IEEE15节点测试系统短路电流

同样的,在得到IEEE15节点测试系统中各个继电保护装置处的故障电流后,通过目标函数式(4)分别计算方案3以及CSM中的2种方案的目标函数值作为对比,结果如表7所示。从表7中可以看出,CSM中的2种方案的目标函数值都明显小于方案3,同时方案2的目标函数值小于方案1,这表明CSM中的2种方案都优于方案3。从图7～8中可以看到,CSM中的2种方案都满足整定要求,即大于最小时间级差。

表7 IEEE15节点测试系统目标函数值

图7 方案1时间级差

图8 方案2时间级差

在实际工程中不仅要考虑到保护整定值优化计算数学模型中目标函数的最小化,还要考虑到时间级差的最小化。

在算例1中,由于主备保护对较少,从图中可以很清晰地看到2种方案的时间级差对比。而算例2中由于系统主备保护装置对的数目较多,从图中很难判断出最佳方案,因此选择通过计算时间级差总和以及平均数的方法判断,如表8所示。表8中列出了2种方案中各继电保护装置的时间级差总和以及平均值,能看出方案1的时间级差小于方案2,在这种情况下即使方案2的目标函数值小于方案1,CSM也会选择方案1进行整定值优化计算,实现系统整体的故障快速切除。采取方案1得到的最优整定值如表9所示。

表8 时间级差最小化分析

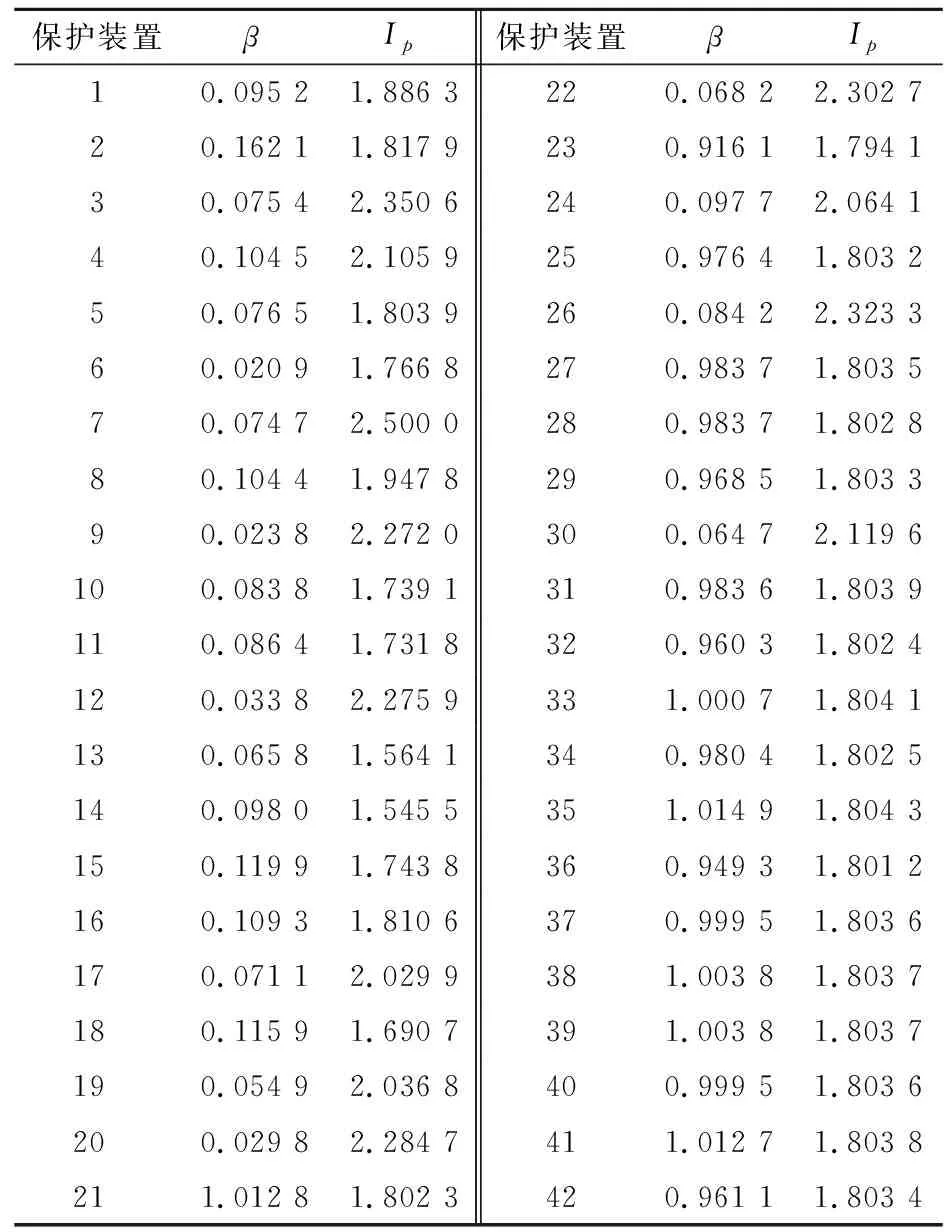
表9 IEEE15节点测试系统最优整定值

5 结论

1) 在该模块中选择的数学模型能够同时最小化主备保护的动作时间。

2) 该模块在分析时不仅考虑了目标函数值的最小化,还考虑了时间级差的最小化。

3) 该模块将动作特性系数作为连续变量,能够在不同系统中自定义选择整定值优化计算方案。

4) CSM中的方案相比较于标准动作时间特性有很大优势,以算例1中的目标函数值为例,CSM中的两种方案目标函数值都明显小于标准动作时间特性下的8.804。因此该模块在配电网自适应过电流保护整定值优化计算中具有更优的有效性,具有良好的应用价值。