基于SLM弧形截面薄壁结构设计及力学性能分析

杨汇荣，史京帅，王艳洋，李忠华，刘 斌

(1. 太原重工股份有限公司 油膜轴承分公司，山西 太原 030024；2. 中北大学 机械工程学院，山西 太原 030051；3. 中北大学 材料科学与工程学院，山西 太原 030051)

0 前言

薄壁结构零件的截面形状设计成带有一定曲率的圆弧状，形成的弧形截面薄壁结构零件可以利用自身的结构特性，提高零件本身的成形高度，同时由于SLM技术加工弧形截面薄壁结构零件的过程中不会产生截面应力畸变，因此设计不同曲率的弧形截面薄壁结构零件，通过对零件自身形成结构约束，提高薄壁结构零件的可成形性。在航空航天、国防、能源和精密物理实验中至关重要的弧形截面薄壁结构零件，要求微米级的轮廓误差和几十纳米的表面粗糙度[1]。传统的切削铣削加工方式，在切削零件的过程中，不仅会诱发大的切削力和高温，而且会迅速且严重地造成刀具磨损，在加工钛合金时这种情况更为严重[2]。TC4弧形截面薄壁结构零件以其轻量化、高强度的特点在航空航天领域得到了广泛的应用[3]。由于薄壁结构零件在长度方向远大于截面方向的厚度与宽度，截面形状复杂，尺寸多变，由此导致TC4薄壁曲面零件的加工难度较大[4]。用传统的铣削加工时，易因大切削力产生的高温与振动致使加工出现问题。对于弧形截面薄壁低刚度零件，其加工参数对振动非常敏感，不适当的加工参数会导致严重的振动，进而导致较大的表面粗糙度。因此，传统铣削加工无法满足高几何精度和高加工质量的要求[5-7]。

薄壁结构零件的壁厚越薄，铣削加工时对刀具的参数要求就越严格。因为随着零件的整体厚度减小，振动对零件加工的影响会逐渐增大[8-10]。为了提高TC4薄壁结构零件的可成形性及成形质量，选用激光选区熔化技术(SLM)——一种金属增材制造技术来加工弧形截面薄壁结构零件，是一种较为合理的方式[11-12]。对SLM而言，加工薄壁结构零件过程中没有振动产生，不会因振动致使零件在加工过程中发生弯折、断裂等[13-14]。这种通过激光器与振镜相结合，将目标区域的粉末熔化，迅速凝结成层，再层层堆积的加工方式，使得在零件加工的过程中，不再有传统刀具与被加工零件之间的接触摩擦，有效避免了振动对加工的影响。对于TC4直薄壁结构零件，采用SLM能成功加工的最小壁厚薄壁结构零件尺寸在1 mm以上，1 mm以下壁厚的零件最大成形高度为14 mm，无法达到尺寸需求[15]。因此，本文通过弧形截面薄壁的合理设计，提高零件的可成形性。

1 弧形截面薄壁结构截面设计

根据每个薄壁结构零件的截面圆心角度分配一个截面标识号，如表1所示，其中列出了截面圆心角度与理论设计挠度。为保证曲面加工精度，采用SLM加工TC4薄壁结构零件。

表1 标称横截面

以长度为20 mm的直薄壁结构零件为设计目标，将弧形截面薄壁的圆弧弦长设计为20 mm，圆心角度从60°开始，以30°为增量，分别设计出圆心角度为90°、120°、150°、180°共五类不同圆心角度的弧形截面薄壁。薄壁结构零件截面的示意图如图1所示，图中θ为截面圆心角度，γ为拱高，l为圆弧弦长，t为壁厚。

图1 截面示意图

2 弧形截面薄壁结构压缩数值模拟

2.1 有限元数值模型建立及网格划分

使用Ansys Workbench软件对TC4弧形截面薄壁的准静态压缩行为做仿真模拟[16]。有限元模型是根据表1中的几何参数建立的。Ansys Workbench分析精度极大程度上受网格类型的影响。经验证，四面体单元用于弧形截面薄壁的几何网格划分，能确保分析的精度，同时可以节省时间[17]。为了在最短的时间内确保分析的高精度，进行了网格灵敏度研究。结果表明，0.1 mm单元的均匀网格为有限元模型提供了合理的收敛性。

2.2 准静态压缩仿真

取壁厚t为1 mm，对上述五种圆心角度的有限元模型进行数值模拟准静态压缩过程，得到的应力云图如图2所示。图2(a)中ST10为壁厚1 mm的直薄壁结构，其在压缩过程中最大应力为1 106.7 MPa，黑色大应力区从零件与基板连接的两端点处向上蔓延，逐渐布满整个零件，零件底面中部区域与侧表面底部为小应力区，呈现出辐射增大的趋势，整体零件变形为底部呈现出“鼓形”变形[18]。图2(b)为壁厚1 mm的CTS1薄壁结构，最大应力为1 296.1 MPa，发生在零件中部与四个顶角处，整体应力分布呈现出五个黑色大应力中心向外辐射减弱的趋势，零件整体变形呈现出中部折弯的趋势。图2(c)为壁厚1 mm的CTS2薄壁结构，最大应力为1 107.5 MPa，整体应力分布与直薄壁结构相似，但是在侧棱面的中部应力较小，黑色大应力区覆盖了整体80%以上的区域，在零件底部仅有一小部分从小应力区过渡到大应力区，整体零件变形出现在底部小应力区向大应力区过渡的区域，沿径向鼓出，同时底部顶角出现向内弯折的现象。图2(d)为壁厚1 mm的CTS3薄壁结构，最大应力为1 339.8 MPa，黑色大应力区分散在零件顶面中部区域及根部与侧壁相交处，整体的应力分布较为均匀，在零件中部两侧为小应力区，以小应力区为辐射中心逐步向外扩撒，均匀过渡到两侧大应力区，大应力向外再次过渡到小应力区，整体零件呈现出顶部扩张、底部内扣的趋势。图2(e)为壁厚1 mm的CTS4薄壁结构，最大应力为1 121 MPa，大应力区主要分布在零件中部及上部，与直薄壁结构分布相似，不同之处为黑色大应力区分为两部分，零件中部有一截过渡区域使得零件变形没有发生在中部，零件整体变形呈现出上部不变、底部出现与CTS3相似的内扣趋势。图2(f)为壁厚1 mm的CTS5薄壁结构，最大应力为1 155.5 MPa，大应力区分布在侧壁靠下的区域及底部端点处，零件中部及上部为应力较大的过渡区域，小应力区从零件底面均匀过渡到底部黑色大应力区，整体变形与CTS4相似，出现底部内扣的现象。

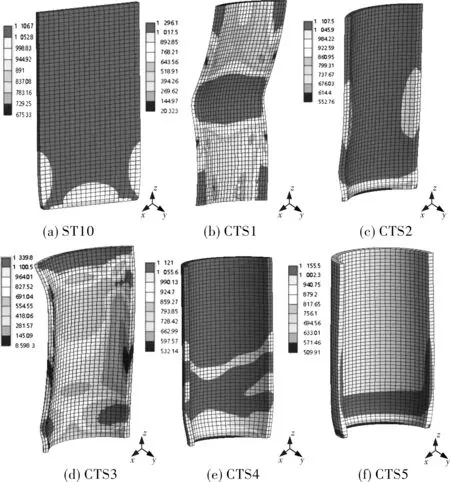
图2 准静态压缩应力云图

将六种薄壁结构在准静态压缩过程中的力载荷与同一时刻对应的位移进行取值并作图，结果如图3所示。

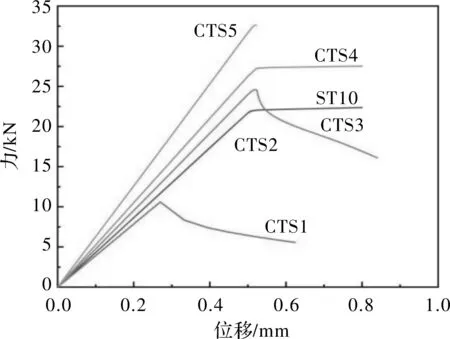
图3 准静态压缩数值模拟力—位移图

从图3中很明显可以看出，在位移0.5 mm之前，代表CTS2薄壁结构的曲线与代表直薄壁结构的曲线ST10几乎重合，说明CTS2薄壁结构在准静态压缩过程中与ST10薄壁结构压缩性能相当。代表CTS1薄壁结构的曲线在位移达到0.25 mm时力载荷达到峰值，之后逐步下降，峰值力仅有10 000 N，而CTS2薄壁结构及ST10薄壁结构均达到了22 000 N。随着圆心角度逐渐增大，CTS3、CTS4、CTS5的峰值力也不断提高，从23 500 N一直上升到33 500 N，说明圆心角度的增加可以提升此类结构的抗压能力。

计算六种薄壁结构在准静态压缩过程中的应力与同一时刻对应的应变并作图，如图4所示。

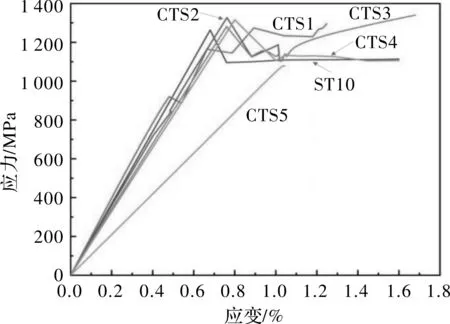
图4 准静态压缩数值模拟应力应变图

从图4中可以看出，CTS1、CTS2、CTS3、CTS4四种不同圆心角度的薄壁结构在图中的斜率(代表压缩模量)均与ST10薄壁结构相当，且最大应变也在一定程度上大于ST10薄壁结构，而CTS5薄壁结构只有最大应变大于ST10薄壁结构，且最大应力及斜率远远小于ST10薄壁结构。

综上所述，CTS1薄壁结构在承受力方面远不如ST10薄壁结构，但是其压缩模量与ST10薄壁结构相当；CTS2薄壁结构在承受力与ST10薄壁结构相当，且压缩模量也相当；CTS3、CTS4两种薄壁结构在承受力与压缩模量方面均优于ST10薄壁结构；CTS5薄壁结构承受力是ST10薄壁结构的1.5倍，但压缩模量稍小；从数值模拟角度来看，CTS2可以替代ST10薄壁结构，CTS3、CTS4两种薄壁结构优于ST10薄壁结构，CTS1、CTS5某些性能则劣于ST10薄壁结构。

3 薄壁结构力学性能测试

3.1 材料特性

本次实验使用的TC4的化学成分如表2所示。

表2 TC4化学元素的质量分数

3.2 工艺参数设置

压缩实验的零件采用E-Plus M150三维设备加工。弧形截面薄壁结构零件高度统一为50 mm，加工工艺参数如下：激光功率为180 W，光斑直径为70 μm，扫描速度为1 000 mm/s，扫描间距为120 μm，粉层厚度为30 μm，扫描策略为短直线填充，各组试件成功成形，零件成品如图5所示。

图5 弧形截面薄壁结构零件

在进行压缩实验之前测量了实际零件的几何尺寸[19]。表3展示的是薄壁结构零件的测量参数，所有薄壁结构零件理论跨度均为20 mm，因此不在表格中体现。薄壁结构零件的名称如CTS1a由圆心角度及壁厚命名，名称中的第一个字母是指圆心角度(C)，第二个字母表示壁厚(T)，后跟截面标识号(S1—S5)，最后一个字母是指壁厚0.5 mm(a)，壁厚0.75 mm(b)和壁厚1 mm(c)。

表3 弧形截面薄壁结构零件规格

薄壁结构零件在SLM加工过程中不可避免地会出现“粘粉”现象，使零件的实际加工壁厚大于理论设计值。因此薄壁结构零件的侧表面会有较大的粗糙度，这种现象随着薄壁结构零件壁厚的增加有所减弱。由图6可以看出，壁厚a指理论壁厚为0.5 mm的薄壁结构零件，其平均误差达到0.08 mm，误差率为15%；理论壁厚0.75 mm的薄壁结构零件平均误差为0.06 mm，误差率为8%；理论壁厚1 mm的薄壁结构零件误差最小，只有0.05 mm，误差率为5%。由此可见，误差率随壁厚增大而减小的幅值逐渐降低，并不能无限地接近0。

图6 圆心角与壁厚的关系

3.3 测试设置

研究不同圆心角度截面的TC4薄壁结构零件的准静态压缩性能，使用(型号为WDW-E200D，级别为0.5)万能试验机，如图7所示。

图7 压缩试样装载设备

由于S1零件挠度小，在压缩过程中会出现零件跨度截面偏离竖直面，使受力方向产生一个微小偏移量，对实验结果产生不规律影响，因此同时加工了支撑底座，底座内尺寸为11 mm×21 mm×5 mm，壁厚为0.5 mm，如图8所示。底座底部设计了0.3 mm厚的底板以避免环氧粘合剂泄漏，然后将S1零件竖直插入底座中并进行调整以确保被压面处于水平面。接着将环氧粘合剂铺在底座内部未被S1零件占用的表面，从而形成厚度约为3 mm的均匀粘合层。最后，让环氧粘合剂在空气中固化24～48 h。环氧粘合剂(型号为靛律超清慢干硬胶)是以环氧树脂为基的双组分耐高温胶粘剂，环氧树脂和固化剂以2∶1的比例混合3 min使用。

图8 底座截面尺寸及零件安装

3.4 测试条件

金属压缩试样准静态压缩测试在室温下进行。压缩试样的装载设备为WDW-E200D型号的万能试验机，加载速度为1 mm/min，最大载荷为10 t，压缩装载在试验机上的图片如图9所示。整个加载过程分为两个阶段：预加载和正式加载。预加载是将载荷增加到100 N并维持30 s，在此期间检查试样是否与试验台两端紧密接触，所有仪器是否都能正常工作，以及载荷是否沿竖直方向施加在试样横截面上[20]。完成所有工作后，试样被卸下。正式加载是重新加载试样直到试件断裂。采用恒速位移增量控制载荷，载荷速率保持0.9 mm/min不变，模拟静载荷，当试件发生断裂，负载开始下降，下降到载荷最大值的85%时，压缩测试停止。

图9 准静态压缩试验过程

3.5 试验结果验证

取t=1 mm的弧形截面薄壁进行准静态压缩试验，变形模式经历了弹性与塑性阶段，其受载力-位移曲线如图10所示。

图10 弧形截面薄壁受载力—位移曲线

五种不同圆心角的弧形截面薄壁在经历弹性阶段之后，随着载荷的增加，在薄壁的棱边中部偏下的部位发生塑性铰弯折的现象。此时的载荷为峰值载荷，随着变形增加，弧形截面薄壁整体呈现出一种菱形类钻石状，最后突然断裂，断口不平整。

由图10的力位移曲线看出，CTS1(圆心角为60°)与CTS2(圆心角为90°)的弧形截面薄壁，在位移达到0.4 mm时，均达到载荷峰值。不同的是，随着位移的增加，CTS1更早地出现棱边断裂。断口随位移增大而增大，载荷迅速减小，CTS2受载力远大于CTS1。在达到载荷峰值后，位移继续增加，弧形截面薄壁没有发生突然断裂，只有棱边有小裂口，中部发生折弯，载荷逐渐减小至0。CTS3(圆心角为120°)在位移达到0.6 mm时载荷达到峰值。发生棱边局部断裂后，载荷逐渐减小，未发生断裂。CTS4(圆心角为150°)在位移达到0.4 mm时载荷达到峰值。随着位移继续增加，载荷维持峰值不变，当位移达到0.7 mm时，棱边断口加大，突然发生断裂，载荷骤减。CTS5(圆心角为180°)在位移达到0.42 mm时载荷达到峰值，载荷出现减小后迅速增加的情形。当载荷增大至1.2倍最大载荷后突然断裂，在载荷峰值处发生突然断裂，载荷骤减为0。从力-位移曲线图中的整体趋势可以看出，弧形截面薄壁结构的断裂位移区间在0.4～0.8 mm之间，且与圆心角度关系很大。只有CTS2与CTS3弧形截面薄壁棱边的中部发生断裂后继续压缩不会发生突然断裂，CTS1、CTS4、CTS5均在载荷达到最大峰值时，由于弧形截面薄壁棱边的中部随位移增大出现突然断裂，致使载荷骤减。从整体来看，圆心角度越大，弧形截面薄壁能承受的载荷峰值越高，而CTS2(圆心角度为90°的弧形截面薄壁)的载荷峰值却超出了CTS3，且其压缩模量(即在图10中弹性阶段的斜率)也比其余四种圆心角度的弧形截面薄壁大，这与其截面特殊的圆心角度有一定联系。

4 结论

本文采用以结构代替材料的思想，将SLM成形钛合金的技术优势与薄壁结构相结合，既避免了使用传统加工方式加工薄壁结构过程中的振动问题，又改善了薄壁结构的力学性能，提高了SLM成形弧形截面薄壁的可成形性，主要结论如下：

(1)基于SLM的钛合金弧形截面薄壁结构能提高1 mm以下弧形截面薄壁结构的可成形性。

(2)针对弧形截面薄壁整体屈曲承载力的最优问题，分别对不同圆心角度的弧形截面薄壁进行准静态压缩实验与数值模拟，在误差允许的范围内，实验与仿真结果相吻合，仿真可以对实验做理论指导。

(3)圆心角度对弧形截面薄壁结构的力学性能有影响。弧形截面薄壁的结构圆心角度最优解为90°，壁厚1 mm的弧形截面薄壁结构试件能承受的最大轴向压力为30 000 N，相较于壁厚1 mm的直薄壁结构提升了36%，且在弹性阶段之后试件没有发生突然断裂破坏，对弧形截面薄壁结构的设计有指导意义。