基于AJSA-BP修正神经网络的TC4钛合金本构关系构建

张宇航，帅美荣，周 路

(太原科技大学 重型机械教育部工程研究中心，山西 太原 030024)

0 前言

TC4钛合金具有高强度、良好的耐腐蚀性、低密度和优异的生物兼容性等优点，广泛应用于航空航天、生物医学、石油化工等领域[1-3]。研究高性能材料的热塑性变形行为及本构关系对于优化成型工艺、提升产品质量具有重要意义。目前，表征材料本构关系主要分为三种类型，分别是机理型、唯象型和神经网络类型[4]，其中Arrhenius是应用最广泛的唯象型模型。国内外的研究学者[5-7]借助于高温热压缩试验，分析了钛合金高温流变行为并构建了基于不同相区和不同变形速率的Arrhenius模型，并用于指导材料塑性成形工艺优化。随着研究的深入，应变量作为影响材料微观组织与调控力学性能的重要指标，在传统Arrhenius本构模型的基础上逐步耦合嵌入，材料的本构关系预测精度显著提升。然而，基于材料高温压缩实验数据的本构模型建立过程复杂，材料常数计算过程容易将实验误差扩大，从而降低模型精度。近年来，BP神经网络具有复杂多变量非线性计算和自学习的能力，其特点是无需提前设置模型，直接对输入数据进行训练，获得数据之间的潜在规律，并以合适的网络作为数据的模型，具有很高的预测精度，逐渐广泛应用于材料性能计算与加工成形领域[8-9]。但BP神经网络也存在收敛速度慢，容易陷入局部最优解的计算瓶颈。

本文通过高温热压缩实验分析TC4钛合金高温流变特性，分别基于应变补偿和AJSA-BP神经网络研究TC4钛合金的本构关系。为了进一步解决BP神经网络预测模型的缺陷问题，基于Matlab平台，采用人工水母搜索算法(Artificial Jellyfish Swarm Algorithm)辅助搜索优化BP神经网络训练过程中的权值和阈值，以提高神经网络性能和稳定性，从而为此类型合金的热成形工艺与性能调控提供理论依据。

1 高温实验材料及流变应力特征分析

1.1 实验材料及方法

本实验采用直径为Ф90 mm的TC4钛合金锻棒，转变温度约为960 ℃[10]，相应的化学成分见表1。在进行热模拟试验前，需要对锻棒进行退火处理以消除内部应力并使其微观结构均匀。具体操作为：将锻棒加热至750 ℃，保温90 min后，空冷至室温。热模拟压缩实验在Gleeble-3800热模拟试验机上进行。

表1 TC4钛合金的主要化学元素的质量分数

热压缩工艺如图1所示，变形温度分别为800 ℃、825 ℃、850 ℃、875 ℃、900 ℃、925 ℃和950 ℃；应变速率分别为0.001 s-1、0.01 s-1、0.1 s-1、1 s-1和10 s-1，变形程度为60%。实验过程中，微型处理系统自动收集相关数据。对收集到的数据进行有效分析及修正后，绘制出TC4钛合金在不同变形条件下的流变应力曲线。

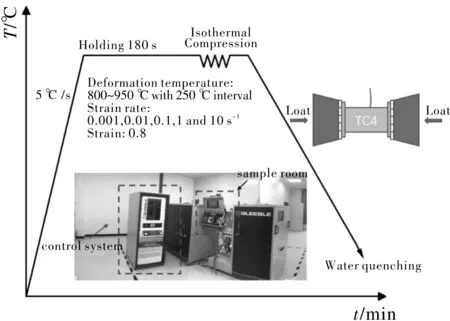
图1 热压缩实验示意图

1.2 TC4高温流变应力特征分析

如图2所示是TC4钛合金在变形温度间隔50 ℃的800～950 ℃、变形速率0.001～10 s-1下的TC4钛合金试样的真应力-真应变曲线。在热变形初期，位错密度随着应变的增加而增加，晶体内部应力逐渐增大直到最大值，导致材料发生加工硬化效应；同时，由于位错交滑移、攀移开始产生作用，迫使位错密度降低，材料发生软化效应；此时，材料加工硬化占主导地位。随着变形的继续，流变应力逐渐降低并趋于稳态，这主要归因于材料发生动态回复和动态再结晶软化效应，材料的硬化速率和软化速率趋于平衡。

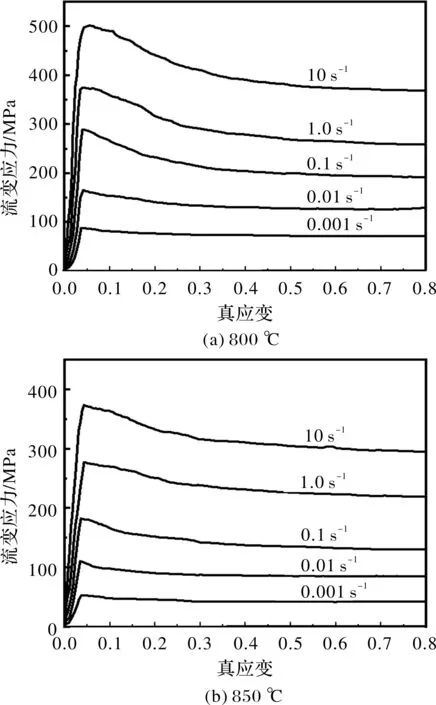
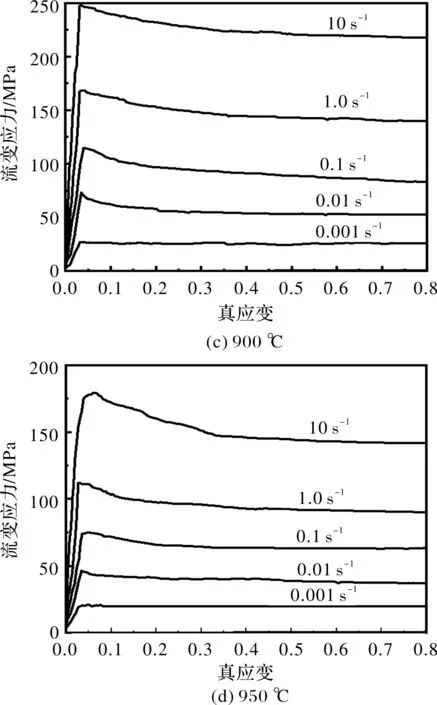
图2 TC4高温流变应力曲线

此外，当变形速率一定时，TC4钛合金的流变应力随温度的升高而降低。温度升高，材料中的晶体缺陷(如位错、空位等)活动加剧，使得材料塑性变形能力增强，动态软化效应显著，流变应力降低[11]。当变形温度一定时，流变应力随应变速率的增大而增大，这主要是由于高应变速率下，短时间内位错在晶内的滑移距离变短，阻力增大，材料流变应力增大[12]。

2 TC4本构模型构建

2.1 基于应变补偿的Arrhenius本构模型构建

采用热变形温度800 ℃、850 ℃、900 ℃、950 ℃下的应力-应变数据建立本构模型，Arrhenius本构模型由指数函数、幂函数、双曲正弦函数三种形式组成[13-15]。

(1)

低应力时

(2)

高应力时

(3)

所有应力适用

f(σ)=A3[sinh(ασ)]n

(4)

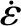
以应变0.3求解材料常数，将式(2)和式(3)带入式(1)，且方程两端同取对数，可得

(5)

(6)

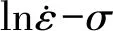
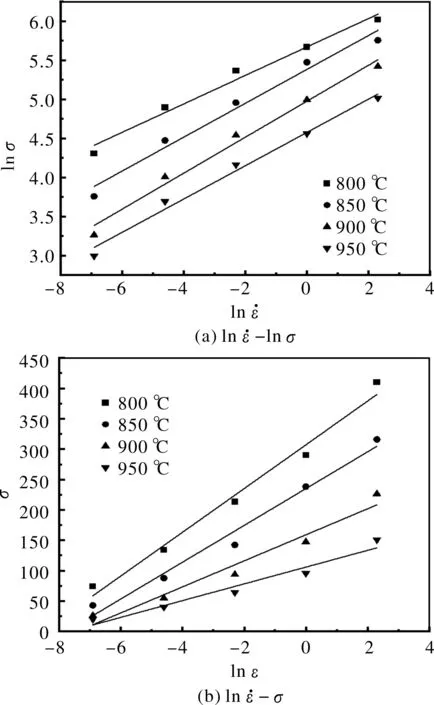
图3 应力与应变速率的关系

将双曲正弦函数式(4)带入式(1)中，且对方程两端取对数：

(7)

(8)

Q/(Rn)=d{ln[sinh(ασ)]}/d(1/T)

(9)

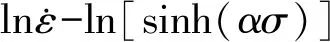
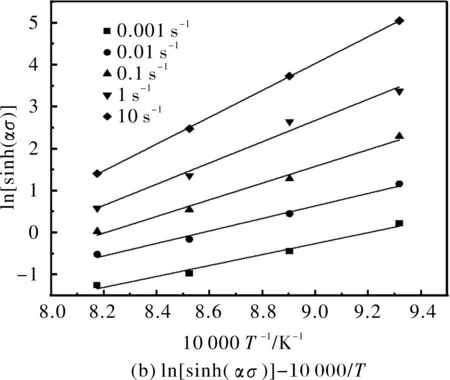
图4 应力与应变速率和温度的关系

引入参数Z表示的Arrhenius本构模型[16]为

(10)

对式(10)两端取对数，则有

lnZ=nln[sinh(ασ)]+lnA3

(11)

线性拟合lnZ-ln[sinh(ασ)]，如图5，得到lnA3= 42.030。

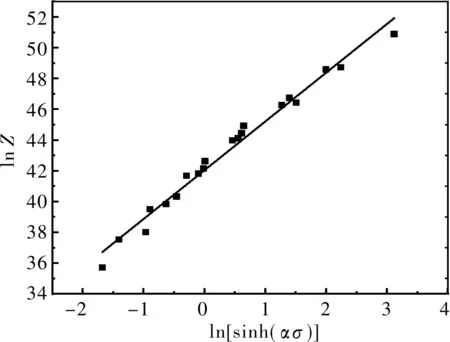
图5 拟合图

但是传统的Arrhenius本构模型并未考虑应变量的影响，故在此基础上构建基于应变补偿的本构模型[17]。以应变0.3为例，求解不同应变量下的TC4材料常数，求取应变区间0.1～0.8，间隔0.1，材料参数结果如表2所示。

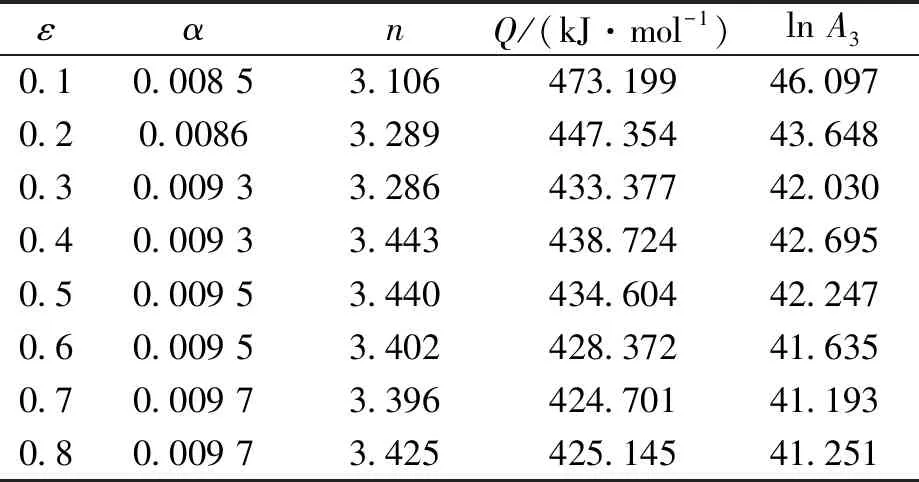
表2 不同应变下的材料参数

以Origin软件对表2中数据进行多项式拟合发现，采用6次多项式表征应变与各参数之间的关系，拟合计算精度最高。各参数拟合关系式如式(12)所示，材料常数拟合曲线如图6所示。

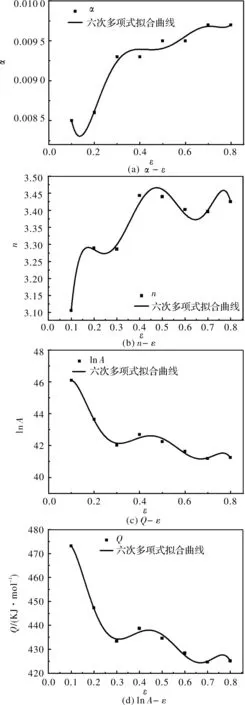
图6 材料参数与应变的多项式拟合曲线

(12)

将各材料常数与应变拟合的多项式代入式(4)，结合式(12)可得基于应变补偿的TC4钛合金本构模型：

(13)

2.2 AJSA-BP神经网络本构关系构建

2.2.1 AJSA-BP神经网络原理

BP神经网络是最常用的一种前向人工神经网络，也是一种有监督学习算法，其全称为“Backpropagation”神经网络，即反向传播神经网络，可以解决复杂的非线性问题[18]；然而BP神经网络也有一些固有缺陷，比如比较容易陷入局部最优值，进而无法继续搜索到更优的解，以及对初始权值和学习率也比较敏感等。

为解决BP神经网络的缺陷问题，本文基于Matlab平台，采用人工水母搜索算法(Artificial Jellyfish Swarm Algorithm，AJSA)对BP神经网络进行优化，提高神经网络性能和稳定性。

人工水母搜索算法是一种受自然界水母觅食行为启发的全局优化算法，它利用水母群体的协同搜索能力来寻找问题的最优解[19]。在算法中，每个水母代表一个个体，对应一个可行解。在初始化时，随机生成一组水母作为初始种群，每个水母的位置表示解空间中的一个解。在人工水母搜索算法中，位置更新公式包含两部分：洋流移动和水母群移动，此两部分目的是使水母能够在搜索空间中进行全局搜索和局部搜索，以寻找最优解。

对于洋流移动部分，水母位置更新公式为

(14)

(15)

由式(14)和式(15)可得洋流移动部分水母位置更新的公式。

Xi(t+1)=Xi(t)+rand(0，1)×(x*-β×rand×μ)

(16)

式中，nPop是水母的数量；x*是当前群体中位置最佳的水母；ec是控制吸引力的因素；u是所有水母的平均位置；df是水母的最佳位置与水母的平均位置之差；β取3，为分配系数。

对于水母群内移动，水母在水母群中运动分为两种类型，主动型(B)和被动型(A)。最早发生的是被动型(A)，其位置更新公式为

Xi(t+1)=Xi(t)+γrand(0，1)(Ub-Lb)

(17)

式中，Ub和Lb分别是搜索空间的上界和下界；γ是运动系数，取0.1。

随着时间推移，A型被动运动转换为B型主动运动，水母运动方向和更新位置是对局部搜索空间的有效利用，表示为

(18)

式中，f是位置Xi的目标函数。

可得B型水母位置更新公式为

(19)

使用人工水母搜索算法可以在全局范围内搜索最优解，以避免BP神经网络陷入局部最优，进而提高BP神经网络收敛速度和稳定性。AJSA-BP神经网络具体实现过程如图7所示。

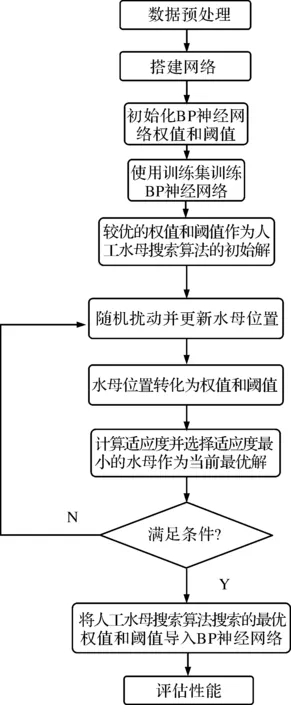
图7 AJSA-BP神经网络流程图

2.2.2 AJSA-BP神经网络本构关系建立

本研究建立AJSA-BP神经网络，由输入层、隐含层、输出层构成，如图8所示。将800 ℃、850 ℃、900 ℃和950 ℃变形温度下的应力应变数据c集按7∶3比例划分成训练集和测试集，训练集2 321组，测试集995组。保持825 ℃、875 ℃和925 ℃变形温度下的应力应变数据集独立，作为验证集。

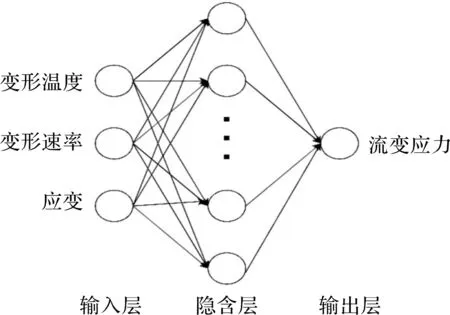
图8 神经网络结构

在训练之前，须得采用mapminmax函数对数据进行归一化处理[20]，值域为[0，1]，对数据进行归一化的主要原因是消除不同特征之间的量纲影响，使得不同特征之间具有可比性。其归一化表达式为

(20)

式中：X表示输入数据；Xmax和Xmin分别对应X的最大值和最小值；Y为归一化后的数据。

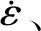
以825 ℃、875 ℃和925 ℃数据验证AJSA-BP神经网络模型准确性和泛化能力，由图9所示，其预测的应力值和实验值基本吻合。预测数据点的绝对误差在20 MPa以内的占94.57%，故可说明该模型能准确预测高温流变曲线，具有良好的泛化能力。

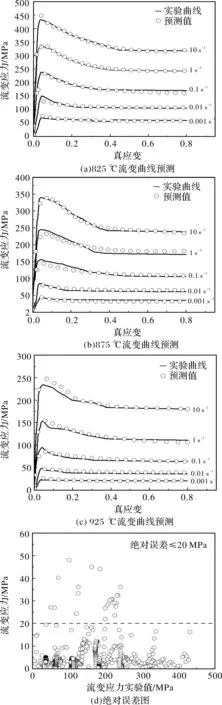
图9 AJSA-BP神经网络流变应力预测

3 本构关系评估

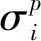
(21)

(22)

计算结果表明，基于应变补偿计算的预测值平均相对误差E为11.48%，模型相关系数R为0.986；预测偏差率不大于15%数据点占81.63%，如图10(a)所示。基于AJSA-BP神经网络应力预测值平均相对误差E为3.83%，模型相关系数R为0.995，预测偏差率不大于15%数据点占95.65%，如图10(b)所示。可以看出，采用AJSA-BP神经网络预测的应力值精度明显高于传统模型预测精度，预测精度约提升了7%，可精确用于材料高温变形工艺计算。

图10 预测值与实验值相关性分析

4 结论

(1)TC4钛合金的流变应力变化与温度负相关，与应变速率呈现正相关性质。在热变形的初期硬化阶段，随应变增加，应力迅速增加到达峰值，随即进入中期应变软化阶段，应变继续增加，应力开始将逐渐降低并趋于稳定，材料具备典型的动态再结晶特性。

(2)构建的基于应变补偿的TC4钛合金新型Arrhenius本构模型，综合考虑了变形温度、应变速率以及应变量的耦合影响，模型预测的应力值平均相对误差E为11.48%，模型相关系数R为0.986，预测值偏差率不大于15%的占比81.63%。

(3)AJSA-BP算法是利用水母群体的协同搜索能力来寻找问题的最优解，以人工水母搜索算法优化BP神经网络的权值和阈值，提升BP的泛化性能和预测精度。基于这种算法优化神经网络预测的应力值平均相对误差E为3.83%，模型相关系数R为0.995，预测值偏差率不大于15%的占比95.65%。由此可见AJSA-BP神经网络模型精度具有更为明显的计算精度优势，可用于精确指导材料高温塑性变形工艺计算。