任意荷载作用下梁-柱的新型实用算法
郭春霞,李银山,孙永涛,李子瑞
(1.西安建筑科技大学 理学院,陕西 西安 710055;2.河北工业大学 机械工程学院,天津 300401;3.天津大学 机械工程学院,天津 300072)
工程中将同时承受轴向压力和横向荷载的梁称为梁-柱[1],梁-柱在工程中的应用非常广泛.例如受风荷载、地震荷载、预应力等轴向压力作用的梁[2-3],油气工程中的悬跨管道往往可以简化为有轴向力影响的简支梁模型[4],加筋机身蒙皮元件在机身弯曲条件下往往还同时承受轴向压缩荷载[5],而作用在梁上的轴向压力,对梁的弯曲特性有较大的影响.此时,梁的内力、应力及变形并不与轴向压力的大小成正比[6],梁-柱本质上是一个非线性静不定问题.因此,准确快速地计算出梁-柱的内力和变形对工程中梁-柱的安全设计具有重要意义.
工程设计人员在设计梁-柱结构时需要计算梁-柱的最大挠度、最大转角和最大弯矩.具有均匀弯曲刚度的梁同时受轴向压力和横向荷载时,其弯曲变形微分方程是一个四阶线性非齐次微分方程,其精确解较为复杂.若采用精确解来分析实际问题则存在计算过程复杂繁琐、计算量大的缺陷[7~9].关于梁-柱的变形分析及应用,已有很多文献从不同的角度进行了研究.陈林靖等[10]基于综合刚度原理和双参数法推导了考虑桩的纵横弯曲的有限差分解,采用 MATLAB 程序语言编制了相应的计算程序,指出对于外露长度和桩顶竖向荷载较大的桩,重力二阶效应是不容忽视的.黄文君等[11]将梁-柱理论的经典解答应用于石油工程中带接头管柱的分析,完整地描述了带接头梁-柱弯曲的三种状态.洪迪峰等[12]结合有限元法和梁-柱的经典解答,提出了广义纵横弯曲法,用牛顿迭代法进行数值求解,分析了非连续性旋转导向钻具的造斜能力.蔡铭等[13]采用初始参数法结合传递矩阵求解了幕墙支撑梁-柱问题并结合实际工程进行了稳定性分析.Mohri等[14]用能量法推导了双对称工字型截面梁-柱在各种横向荷载和轴力联合作用下的解析解,并分析了梁-柱的后屈曲行为.
随着计算机的发展,出现了一系列求解梁-柱问题的新方法.Dado等[15]提出了一种基于非线性控制微分方程的积分最小二乘法,将梁的转角用多项式表示,可分析棱柱式和非棱柱式悬臂梁-柱的弯曲问题;Arboleda等[16]采用经典矩阵法研究了轴向力对双参数弹性地基上梁-柱变形的影响.Hatami等[17]利用微分变换法将梁的变形表示为多项式,研究了悬臂梁-柱弯曲时的挠度;Ressell[5]利用梁-柱的经典解答,讨论了两种处理广义梁-柱问题的数值解法.李晓姣[18]提出了分析梁-柱问题的辛本征值法.Areizo等[19]基于微分变换方法对横向荷载和轴向约束作用下的锥形梁-柱进行了大挠度分析,提高了计算效率.连续分段独立一体化积分法是李银山等[20-22]提出的一种求解力学中有关微分方程问题的有效方法,与计算机软件相结合,具有求解精度高、速度快的特点.
本文在连续分段独立一体化积分法的基础上,采用渐进积分法研究了梁-柱的弯曲变形问题,得出了简支梁-柱在各种荷载作用下的最大弯矩和最大挠度、最大转角关于轴力放大系数的表达式,所得解答为简单的多项式,便于理解和计算.并将渐进积分法的计算结果与经典的精确解进行比较验证,在迭代仅6次的情况下即可达到满足工程需要的精度,大大提高了计算速度.
1 横向分布力作用下的简支梁-柱
1.1 基本方程和边界条件
设长为l、抗弯刚度为EI的梁,仅承受横向分布荷载q(x).轴向坐标为x,挠度为v.梁的小挠度四阶导数微分方程为[1]
(1)
设长为l、抗弯刚度为EI的杆,仅承受轴向集中荷载F.轴向压力作用下杆的四阶导数微分方程为[1]
(2)
欧拉临界力公式为
(3)
其中:Fcr为临界压力;μ为与支承有关长度系数;α为集中力临界力系数.
若略去剪切变形和梁轴线缩短的影响,由式(1)和式(2)叠加得到,同时承受横向分布荷载和轴向集中力F作用下梁-柱的微分方程为
(4)
简支梁边界条件
v(0)=0,EIv″(0)=0
(5a)
v(l)=0,EIv″(l)=0
(5b)
为将方程(4)无量纲化,令
(6)
将式(6)代入式(4),可得梁-柱的无量纲微分方程
(7)
本节研究同时承受横向均布荷载 (此时q(x)=-q)和轴向集中力F作用下的直梁,如图1所示.

图1 横向均布荷载作用的简支梁-柱
由式(7)可知无量纲微分方程为
(8)
式中
α=π2
(9)
则无量纲化后边界条件(5)可简写为
V(0)=0,V″(0)=0
(10a)
V(1)=0,V″(1)=0
(10b)
1.2 渐进积分法
为求解微分方程(8),构造迭代方程如下.
(11a)
(11b)
第一次近似:选取无轴向力作用的简支梁的挠度为初始曲线V[0](X).
结合边界条件
(12a)
(12b)
由连续分段独立一体化积分法可得方程(11a)的解为
(13)
将(13)代入(11b),可求出第一次近似变形曲线.基本方程为
(14)
边界条件
(15a)
(15b)
由连续分段独立一体化积分法可解出迭代一次后的挠度函数为


(16)
1.3 弯矩和变形的最大值
由(16)式可求出跨中的最大挠度为
(17a)
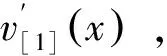
(17b)
根据EIv″(l/2)可得最大弯矩为
(17c)

(18)
η[1](κ)、χ[1](κ)和λ[1](κ)均为大于1的数,表示轴力对最大挠度、最大转角和最大弯矩的影响,称为轴力放大系数.
同理可得,第二次迭代后的最大挠度、最大转角和最大弯矩的放大系数分别为
η[2](κ)=1+1.003 4κ+1.003 8κ2
(19a)
χ[2](κ)=1+0.986 96κ+0.985 69κ2
(19b)
λ[2](κ)=1+1.028 1κ+1.031 6κ2
(19c)
依次类推,可得迭代六次后的最大挠度、最大转角和最大弯矩放大系数
η[6](κ)=1+1.003 4κ+1.003 8κ2
+1.003 9κ3+1.003 9κ4+1.003 9κ5+1.003 9κ6
(20a)
χ[6](κ)=1+0.986 96κ+0.985 69κ2
+0.985 55κ3+0.985 54κ4+0.985 53κ5+0.985 53κ6
(20b)
λ[6](κ)=1+1.028 1κ+1.031 6κ2+1.032 0κ3+
1.032 0κ4+1.032 0κ5+1.032 0κ6
(20c)
根据本文的方法,无论迭代几次,梁-柱的内力和变形均可表示为类似于式(20)的简单多项式,很容易求出其数值.
本问题的精确解[1]如下
(21a)
(21b)
(21c)
式中:
(22)
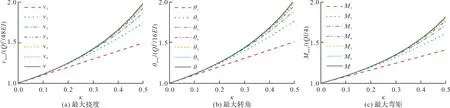
本文迭代6次的最大挠度、最大转角和最大弯矩与精确解的对比情况如图2所示.
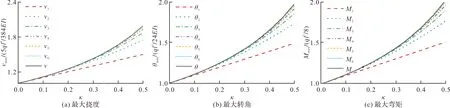
图2 前六次迭代时最大转角、最大转角和最大弯矩与精确解的对比
从图2可以看出,横向均布荷载作用下的两端铰支梁-柱迭代计算出的最大变形和弯矩均随迭代次数的增加而逐渐趋近于精确解.
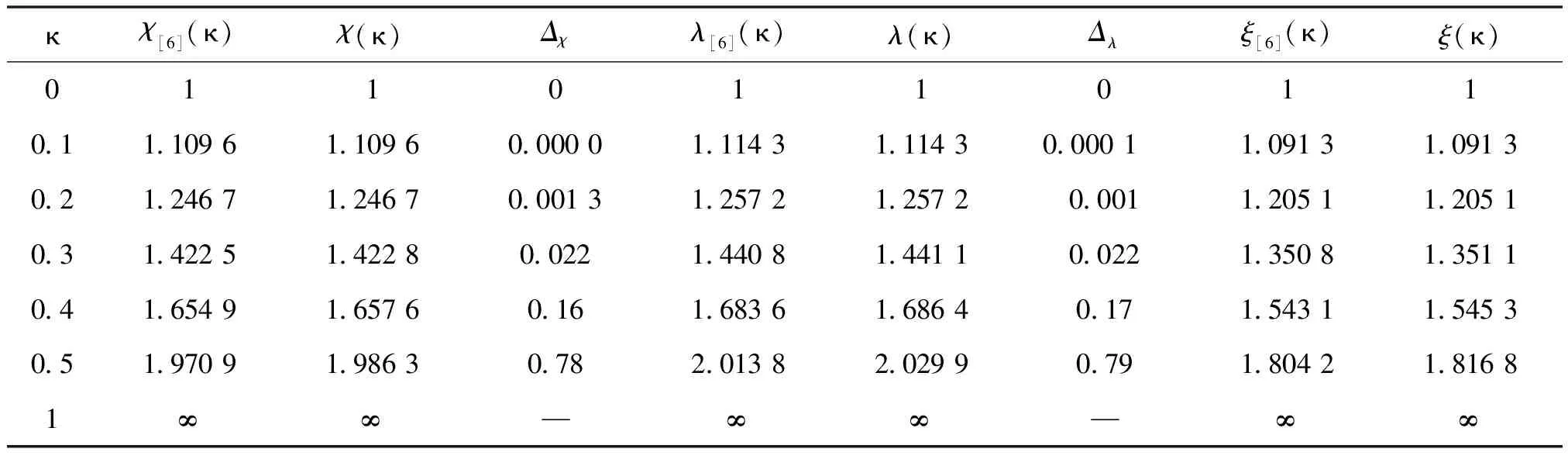
利用渐进积分法求解,迭代六次时最大挠度放大系数η(κ)、最大转角放大系数χ(κ)和最大弯矩放大系数λ(κ)的计算结果如表1所示,并与精确解进行了对比.
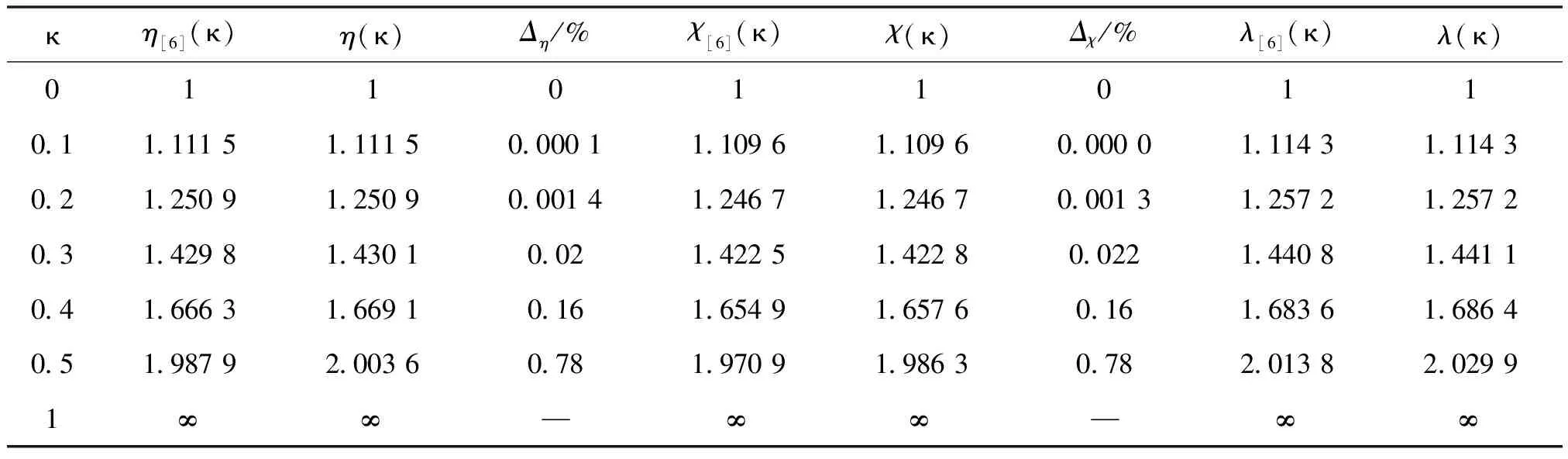
表1 放大系数η(κ),χ(κ)和λ(κ)
从表1可以看出,当κ∈[0,0.5]时,即当梁所受的轴向力是欧拉临界力的1/2以内时,本文计算出的结果与精确解的误差在1%以内,且轴力对最大变形和最大内力的影响均随κ的增加而增加,当κ=0.5时,梁的最大变形和内力均约是没有轴向力时的2倍.
2 横向集中力作用下的简支梁-柱
2.1 基本方程和边界条件
本节研究同时承受横向集中力Q和轴向集中力F作用的简支梁-柱,如图3所示.
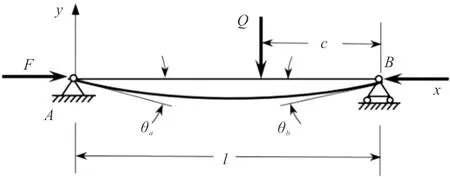
图3 有一横向集中荷载作用的纵横弯曲梁
由式(7)可知此时无量纲微分方程为
(23)
式中
α=π2
(24)
无量纲边界条件为
V(0)=0,V″(0)=0
(25a)
V(1)=0,V″(1)=0
(25b)
2.2 渐进积分法
构造迭代方程如下.
(26a)
(26b)
第一次近似:选取无轴向力作用的梁挠度为初始曲线v[0](x).基本方程
(27a)
(27b)
边界条件和连续光滑条件
(28a)
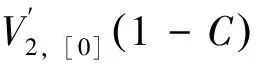
(28b)

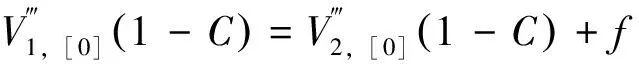
(28c)
(28d)
式中
(29)
由连续分段独立一体化积分法解得
(30a)
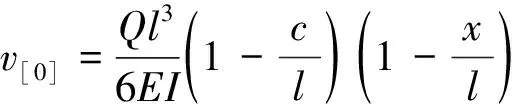
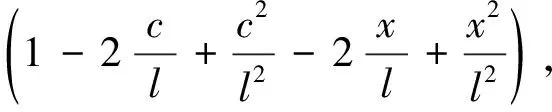
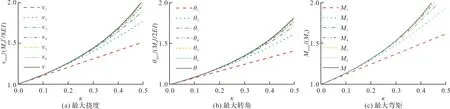
(l-c (30b) 由式(26b)求第一次近似变形曲线,基本方程为 (31a) (31b) 边界条件和连续光滑条件为 (32a) V1,[1](1-C)=V2,[1](1-C), (32b) (32c) (32d) 由连续分段独立一体化积分法解得挠度函数为 (33a) (33b) 将x=c=l/2代入式(33a),得迭代一次后的最大挠度为 (34a) (34b) 由EIv″(l/2)得最大弯矩为 (34c) (35) 将(33)式代入(26b)式,进行第二次迭代,可得最大挠度放大系数、最大转角放大系数和最大弯矩放大系数分别为 χ[2](κ)=1+0.986 96κ+0.985 69κ2 (36a) λ[2](κ)=1+1.028 1κ+1.031 6κ2 (36b) ξ[2](κ)=1+0.822 47κ+0.811 74κ2 (36c) 同理迭代六次后可得最大挠度放大系数、最大转角放大系数和最大弯矩放大系数分别为 χ[6](κ)=1+0.986 96κ+0.985 69κ2+0.985 55κ3+ 0.985 54κ4+0.985 53κ5+0.985 53κ6 (37a) λ[6](κ)=1+1.028 1κ+1.031 6κ2+1.032 0κ3+ 1.032 0κ4+1.032 0κ5+1.032 0κ6 (37b) ξ[6](κ)=1+0.822 47κ+0.811 74κ2+0.810 70κ3+ 0.810 58κ4+0.810 57κ5+0.810 57κ6 (37c) 本问题的精确解[1]如下. (38a) (38b) (38c) 式中: (39) 迭代六次后,每次迭代的最大挠度、最大转角、最大弯矩与精确解的对比情况如图4所示.利用渐进积分法求解,迭代六次时最大挠度放大系数χ(κ)、最大转角放大系数λ(κ)和最大弯矩放大系数ξ(κ)的计算结果如表2所示,并与精确解进行了对比. 表2 放大系数χ(κ)、λ(κ)和ξ(κ) 图4 前六次迭代时最大挠度、最大转角和最大弯矩与精确解的对比 从图4和表2可以看出,当κ∈[0,0.5]时,本文的解答与精确解的误差在1%以内,说明在这一范围内,渐进积分法的计算结果可以满足实际工程需要,是计算梁-柱问题的一种可靠方法. 利用渐进积分法也可求解由力偶引起的简支梁-柱的弯曲,方法与前两节相同,只是基本方程和边界条件略有区别,文中不做详细推导,仅对计算过程进行简要说明,并附计算结果. 本节研究力偶引起的梁-柱的弯曲问题,如图5所示,简支梁-柱若有两个力偶Ma,Mb分别作用于杆的A,B两端. 由式(7)可知无量纲微分方程为 (40) 无量纲边界条件为 V(0)=0,V″(0)=ma (41a) V(1)=0,V″(1)=mb (41b) 式中 (42) 构造迭代方程,选取无轴向力作用的梁挠度为初始曲线V[0](X). 由连续分段独立一体化积分法解得 (43) 第一次近似变形挠度函数为 (44) 为讨论方便,假设Mb=Ma=M0,则最大挠度出现在跨中截面 (45a) 最大转角为 (45b) 最大弯矩为 (45c) (46) 依次进行迭代,迭代六次后可得最大挠度放大系数、最大转角放大系数和最大弯矩放大系数分别为 λ[6](κ)=1+1.028 1κ+1.031 6κ2+1.032 0κ3+ 1.032 0κ4+1.032 0κ5+1.032 0κ6 (47a) ξ[6](κ)=1+0.822 47κ+0.811 74κ2+0.810 69κ3+ 0.810 58κ4+0.810 57κ5+0.810 57κ6 (47b) ζ[6](κ)=1+1.233 7κ+1.268 3κ2+1.272 7κ3+ 1.273 2κ4+1.273 2κ5+1.273 2κ6 (47c) 本问题的精确解[1]如下, (48a) (48b) (48c) 迭代六次后,每次迭代的最大挠度、最大转角、最大弯矩与精确解的对比情况如图6所示. 图6 前六次迭代时最大挠度、最大转角和最大弯矩与精确解的对比 利用渐进积分法求解,迭代六次时最大挠度放大系数λ(κ)、最大转角放大系数ξ(κ)和最大弯矩放大系数ζ(κ)的计算结果如表3所示,并与精确解进行了对比. 表3 放大系数λ(κ)、ξ(κ)和ζ(κ) 从图6和表3可以看出,当κ∈[0,0.5]时,本文的解答与精确解的误差在1%以内,说明在这一范围内,渐进积分法的计算结果可以满足实际工程需要,是计算梁-柱问题的一种可靠方法. (1)本文从力学模型研究入手,建立了小挠度简支梁-柱在各种荷载作用下求解的通用模型,推导出梁-柱变形的一般方程和程序化求解内力和变形的通用程序,用 Maple语言开发出相应的求解程序; (2)采用渐进积分法求解了横向分布力、横向集中力和力偶等三种荷载情况下简支梁-柱的变形问题,得出了最大挠度、最大转角和最大弯矩的简单多项式表达式; (3)关于梁-柱的弯曲问题,以铁摩辛柯为代表的复杂三角函数的精确解,需查表使用,不便于工程应用;有限单元法只能得到数值解,无法得到解析式.本文用渐进积分法进行求解,采用横向均布载荷作用下满足基本方程和边界条件的梁弯曲函数作为初函数,开始迭代计算,得到结果是简单的多项式函数.由于采用计算机求解计算速度快,荷载和刚度不需要简化,可以得到解析解,求解过程简洁方便、快速准确; (4)本文提出的渐进积分法对实际工程中的梁-柱计算具有重要的指导意义.此方法可以推广到任意荷载和一般边界条件的梁-柱,另文介绍.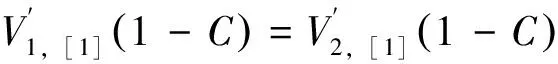
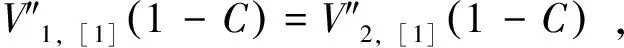
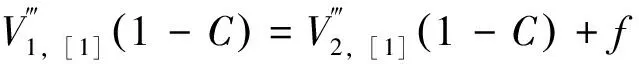


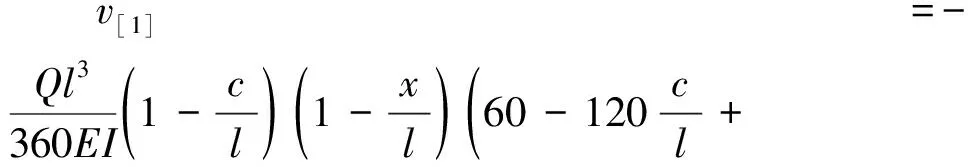


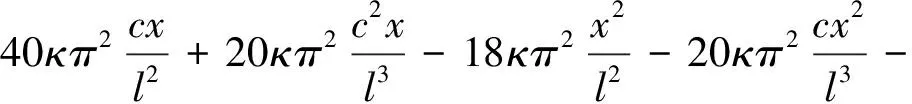
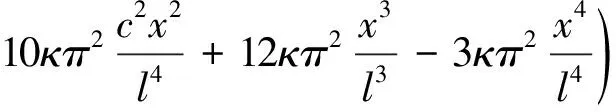
2.3 弯矩和变形的最大值
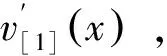
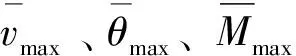
3 由力偶引起的简支梁-柱的弯曲
3.1 基本方程和边界条件
3.2 渐进积分法
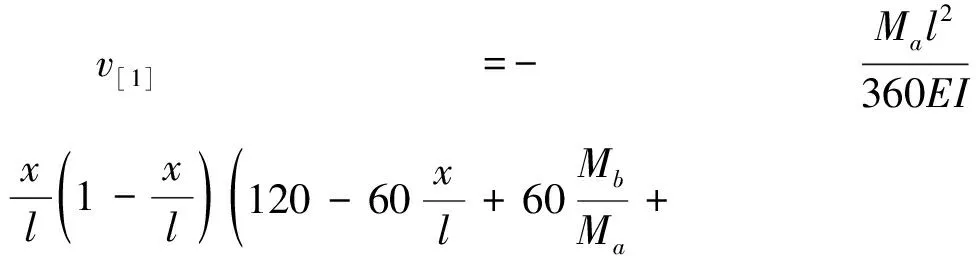
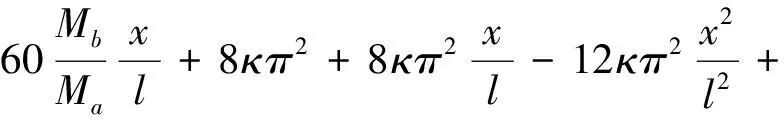
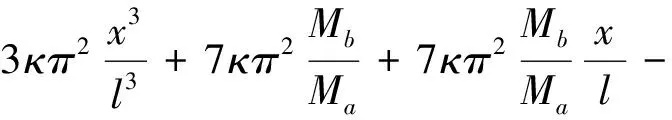
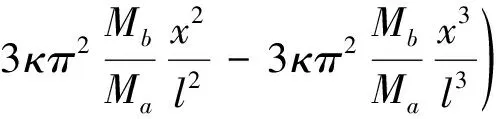
3.3 弯矩和变形的最大值
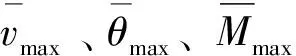

4 结论

