典型参数对黏性干扰效应影响研究

杨依峰，陈 浩，陈 刚，张昱煜，于江鹏

（北京航天长征飞行器研究所，北京，100076）

0 引 言

航天飞行器在高空高速飞行时，壁面会形成异常厚的黏性边界层，边界层内的气体流动与外部的无黏气流之间形成强烈的耦合作用，致使壁面压力发生变化，从而对飞行器气动力、稳定性、操纵性产生一定影响，严重情况下可能导致飞行器气动设计失效［1］。国内外对黏性干扰问题开展了大量研究，美国在航天飞机研制过程中通过理论分析和风洞试验对各类黏性干扰问题开展了一系列研究分析，积累了大量研究成果［2-5］。中国对黏性干扰效应的研究起步相对较晚，龚安龙等［6］提出了一种适用于高升力飞行器天地相关性研究的黏性干扰相关参数，王刚等［7］提出了黏性干扰效应作用下风洞数据-飞行数据的组合关联参数，张益荣等［8］建立了一种翼身组合体黏性干扰效应模型。

本文采用CFD数值方法对对边界层流动有重要影响的飞行参数——高度（雷诺数）和壁温（壁温比）开展研究，分别以尖楔外形和典型后缘舵航天飞行器为研究对象，模拟不同参数下的流场结构，从而获得高度和壁温对黏性干扰效应的影响。

1 计算方法

本文的CFD数值方法采用Navier-Stokes方程作为流动控制方程，其积分形式为

式中V为控制体体积；Q为守恒变量矢量；Ω为控制体表面的面积；f为通过表面Ω的净通量矢量，包含黏性项和无黏项；n为表面Ω的单位外法向矢量。

控制方程中的无黏通量项的离散采用Van Leer格式，时间离散方法采用LU-SGS隐式时间推进格式。

采用上述仿真方法对升力体标模（见图1）进行计算，风洞试验条件为Ma=8，并将计算结果与风洞试验数据进行对比（见图2），二者吻合较好，验证了程序模拟高超声速流场的可靠性。

图1 风洞标模外形Fig.1 Wind tunnel calibration model

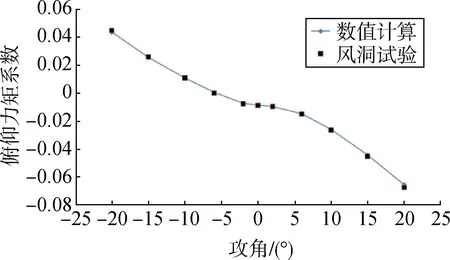
图2 数值计算与风洞试验对比曲线Fig.2 Comparison curve between numerical calculation and wind tunnel test

2 尖楔流动分析

本文以半楔角为10°的尖楔（见图3）为研究对象，采用第1节的计算方法对不同高度、壁温条件下的流场进行仿真，研究高空低雷诺数黏性干扰影响以及壁温（壁温比）边界信息对近壁面流动的影响。尖楔模型长度为1 m，计算网格为结构网格（见图4），第1层网格高度为1×10-5m，网格总量为22万个。

图3 尖楔外形（半楔角为10°）Fig.3 Tip wedge profile (half wedge angle 10°)

图4 尖楔外形网格Fig.4 Tip wedge profile grid

2.1 高度对尖楔流动影响

对于可压缩层流边界层，其厚度δ的增长规律基本符合式（2）定义，其中Ma∞为自由来流马赫数，Rex为当地雷诺数，边界层厚度与自由来流的Ma∞成正比，与当地雷诺数的平方根成反比。由于高空大气密度与低空大气密度存在量级上的差异，从而使当地雷诺数差异较大，进而导致边界层厚度存在较大差异。

图5 为尖楔在Ma=10、攻角为0°、壁温为1 000 K、不同高度（40 km、50 km、60 km）时的马赫数云图。

由图5可知，随着高度增加，雷诺数减小，尖楔边界层厚度增大。此外，在高度为60 km时，由于边界层厚度很大，边界层外的无黏流动受边界层影响发生了很大的改变，外部无黏流动的改变反过来又会影响边界层的发展，这样边界层内的黏性流动与边界层外的无黏流动相互作用，形成了复杂的黏性干扰。另外，厚边界层对边界层外的无黏流产生一个较大的位移效应，导致无黏计算的尖楔外形比实际外形厚很多，增大了尖楔表面激波角，从而使尖楔表面压强系数Cp增大，如图6所示。因此，在高空低雷诺数条件下，边界层黏性干扰增强。

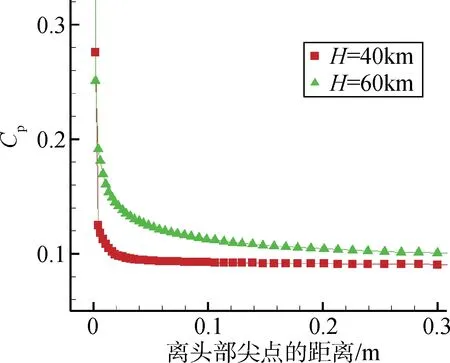
图6 不同高度条件尖楔表面压强系数曲线Fig.6 Curve of wedge surface pressure coefficient at different altitudes

2.2 壁温对尖楔流动影响

对于平板层流边界层，边界层厚度δ增长规律也符合以下规律：

式中Tw为壁面温度；Te为边界层外边界温度；Ree为边界层外边界雷诺数。

边界层厚度除了与雷诺数有关外，还与壁面温度和边界层外边界温度也相关。由于边界层外边界温度需要通过流场求解才能得到，不利于分析温度对边界层的影响规律，这里使用壁温Tw和壁温比(Tw/Te)来研究壁面温度对边界层的影响。

图7 给出了Ma=10、高度为60 km、不同壁温（247 K、1 000 K、2 000 K）情况下的尖楔马赫数云图。

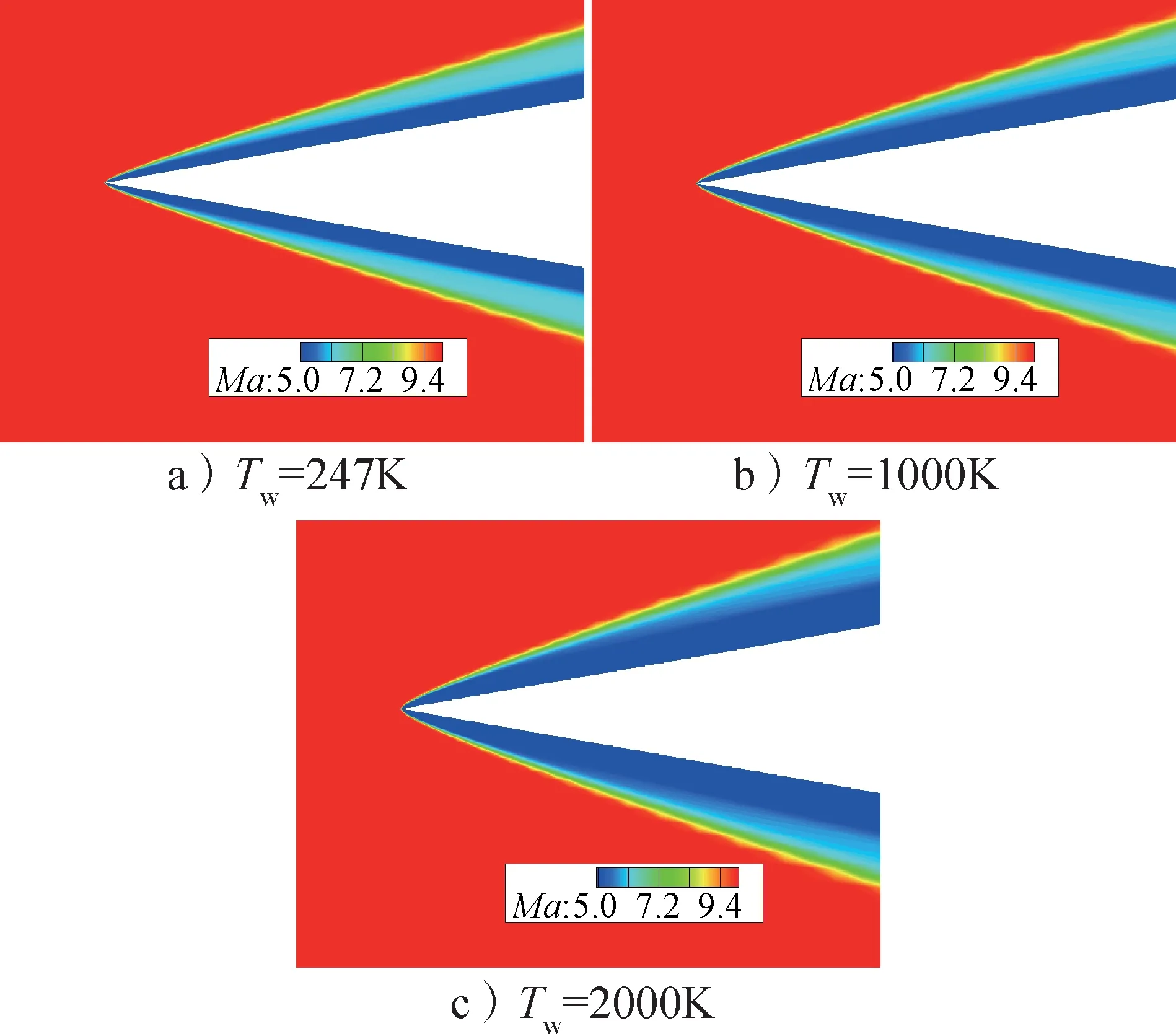
图7 不同壁温条件马赫数云图Fig.7 Mach number contour under different wall temperature conditions

从图7中可以看出，随着壁温的增大，尖楔边界层逐渐增厚，黏性干扰逐渐增强，其激波角也逐渐增大，使尖楔表面压强系数增高，如图8 所示。因此，壁温对黏性干扰存在影响，随着壁温的增大，黏性干扰增强。

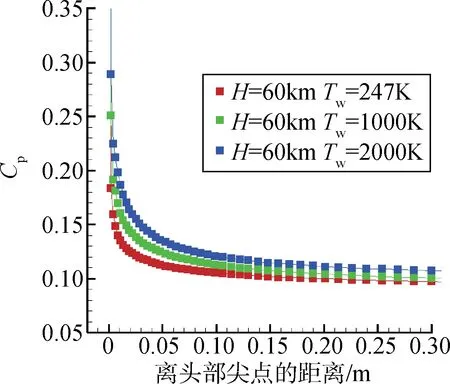
图8 不同壁温条件尖楔表面压强系数曲线Fig.8 Curve of pressure coefficient on wedge surface under different wall temperature conditions

3 航天飞行器流动分析

以后缘舵航天飞行器为研究对象，采用上述计算方法对不同高度、不同壁温条件下的流场进行仿真，研究黏性干扰对飞行器舵效的影响。飞行器全长3 m，计算网格为非结构网格（见图9），第1层网格高度为1×10-5m，网格总量400万个。

图9 航天飞行器网格Fig.9 Space vehicles grid

3.1 高度对航天飞行器流动影响

图10 给出了飞行器舵偏角为10°、Ma=10、攻角为0°、不同高度（40 km、60 km）时的展向截面马赫数云图。

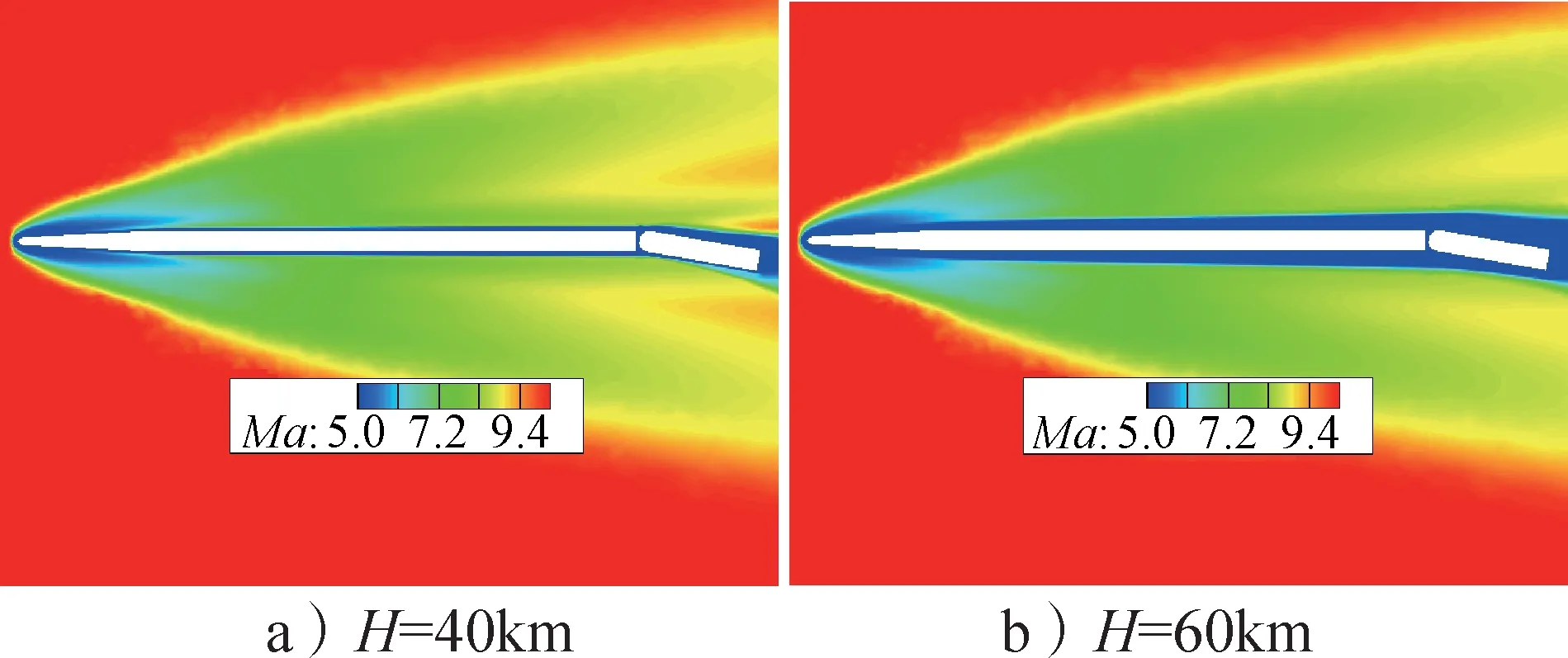
图10 不同高度条件马赫数云图Fig.10 Mach number contour at different altitudes

由图10 可知，随着高度增加，雷诺数减小，飞行器机翼边界层厚度增大，其对空气舵附近流场产生黏性干扰，致使空气舵下表面压强系数减小。舵面压强系数随高度变化规律与尖劈不同，其原因为尖劈激波与边界层存在较强的干扰，边界层增厚致使激波角度增大，从而使尖劈表面压强系数增大。而舵面受机翼边界层影响，高度为60 km时从机翼发展来的厚的边界层包裹空气舵，致使空气舵激波角度较小，舵面压强降低，见图11、图12。高度为60 km时的舵效比高度为40 km时的舵效减小约42%，见图13。

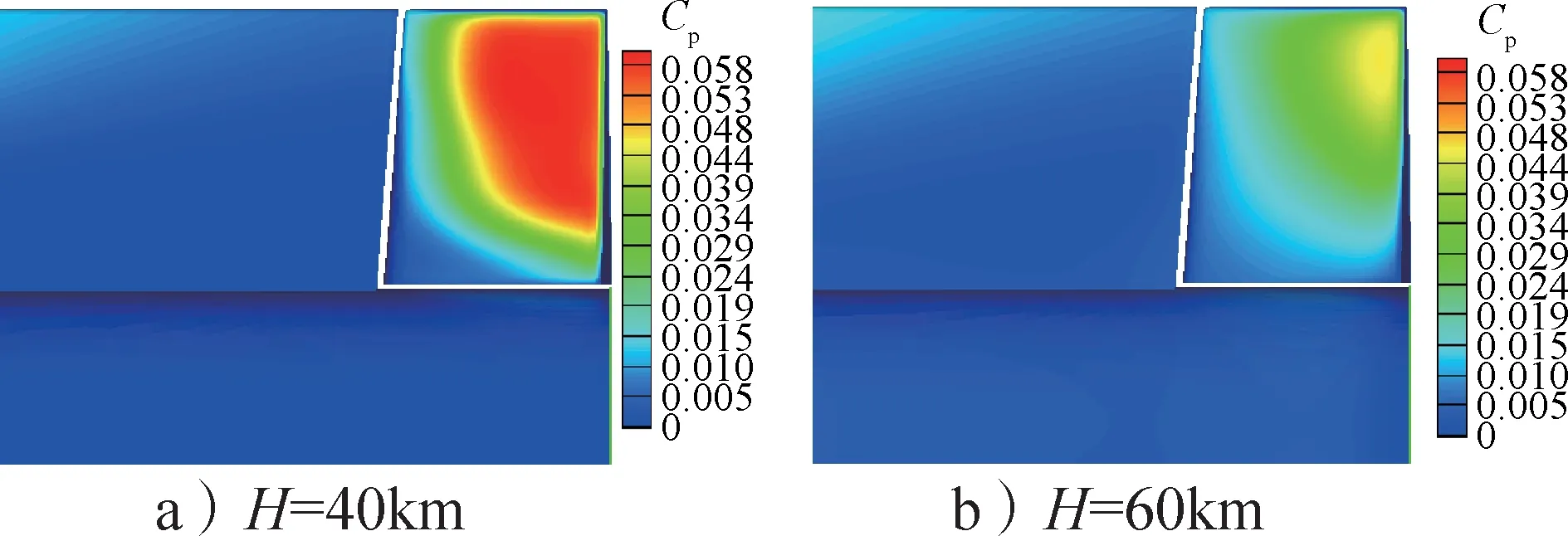
图12 不同高度条件壁面压强云图Fig 12 Pressure coefficient contour at different altitudes

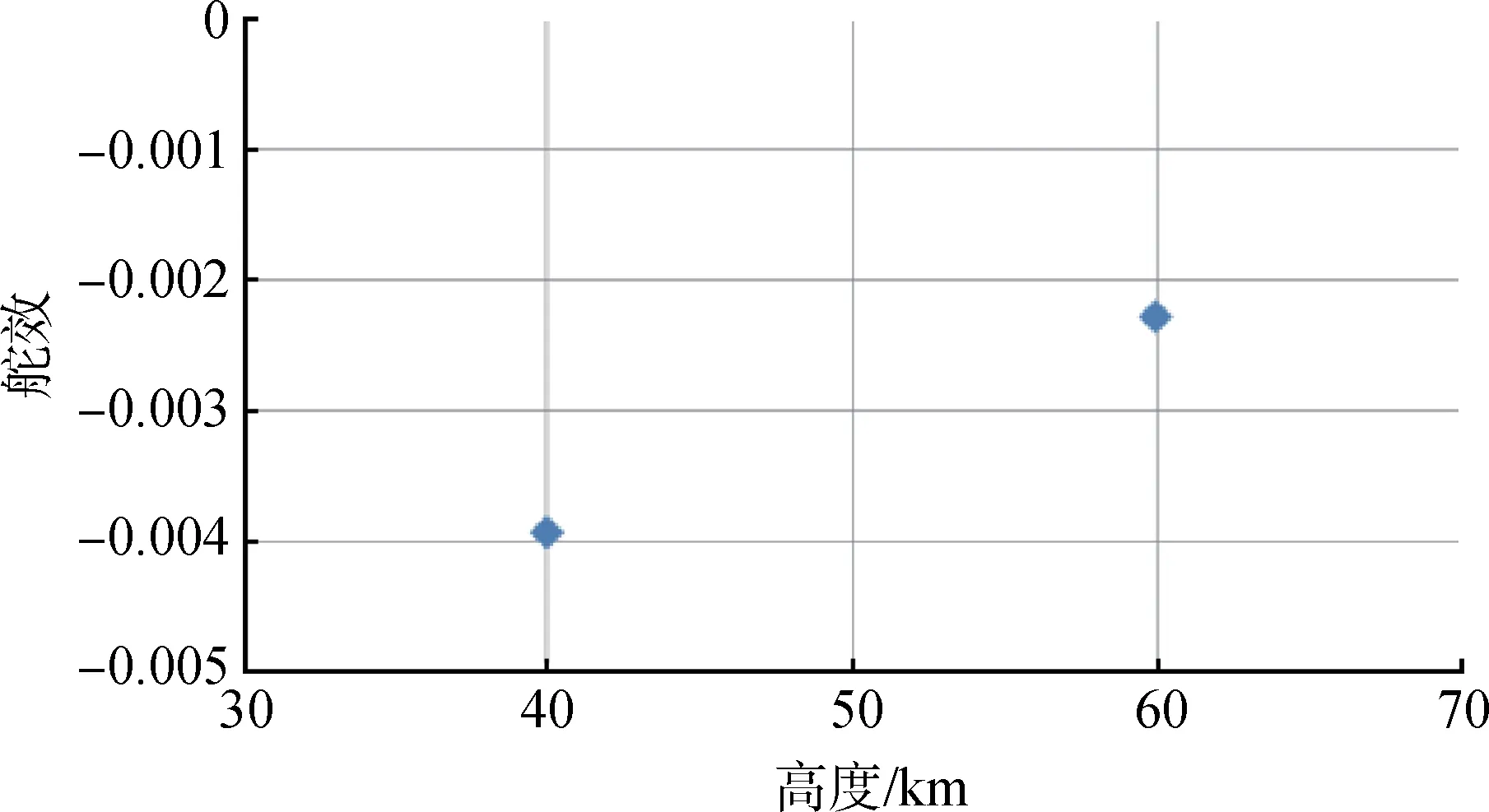
图13 不同高度条件舵效对比Fig.13 Comparison of rudder efficiency at different altitudes

3.2 壁温对航天飞行器流动影响

图14 给出了飞行器舵偏角为10°、Ma=10、攻角为0°、高度为60 km 时不同壁温（550 K、1 250 K、2 500 K）条件下展向截面马赫数云图。随着壁温增大，飞行器机翼边界层厚度增厚，其对空气舵黏性干扰增强，致使空气舵下表面压强系数减小（见图15）。飞行器舵效随着壁温增大而减小（见图16），壁温为2 500 K 时的舵效比壁温为550 K 时的舵效减小约28%。

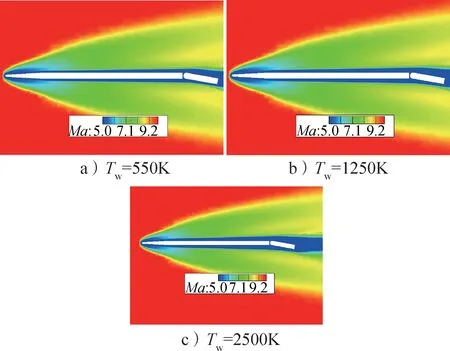
图14 不同壁温条件马赫数云图Fig.14 Mach number contour under different wall temperature conditions

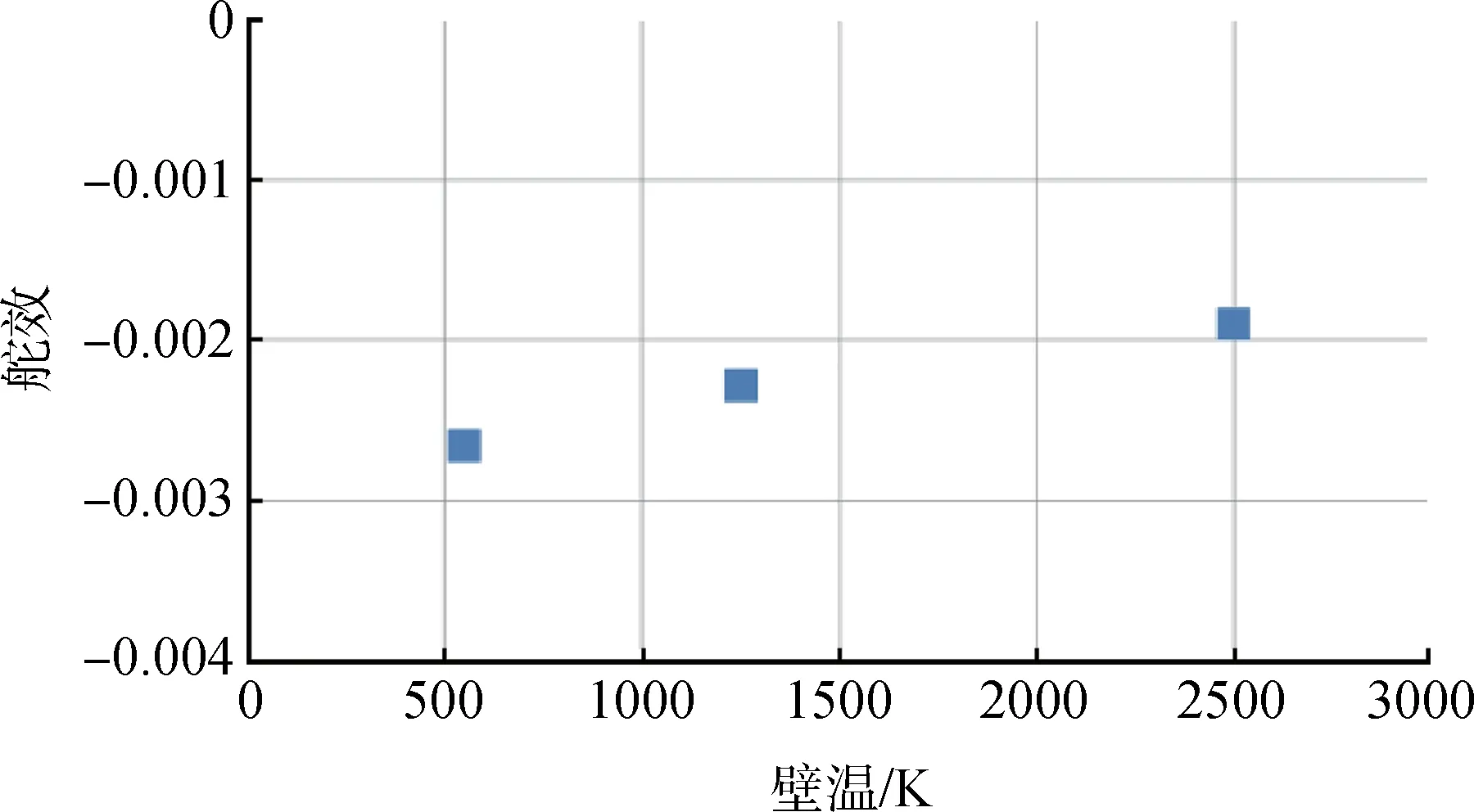
图16 不同壁温条件舵效对比Fig.16 Comparison of rudder efficiencyunder different wall temperature conditions

4 结束语

本文以尖楔外形为研究对象，开展了高度、壁温对壁面边界层流动的影响研究，获得了黏性干扰流场结构变化及影响规律。此外，针对典型后缘舵航天飞行器，开展了黏性干扰对飞行器舵效的影响分析。通过研究，本文得出如下结论：

a）高度和壁温参数对黏性干扰有重要影响，随着高度增加、壁温增大，黏性干扰效应增强，激波角度增大，壁面压强增大。

b）针对典型后缘舵航天飞行器，高度、壁温对机翼边界层流动有较大影响。随着高度增加、壁温增大，边界层逐渐增厚，对舵面干扰影响增强，造成飞行器空气舵表面压强系数降低，致使其舵效显著减小。