基于SiC气凝胶的热防护结构隔热性能分析及优化
杭子轩,戴 婷,李 珺
(中南大学航空航天学院,长沙,410083)
0 引 言
高速飞行器在高马赫数飞行时会面临极端恶劣的气动加热环境[1],气动热效应不仅会对飞行器壁面材料产生负面影响,也会对舱内仪器设备的正常工作造成破坏[2]。为了避免出现飞行器结构外形烧蚀、内部设施无法正常运行的情况,必须对飞行器进行热防护设计[3-4]。典型的热防护结构主要为烧蚀、辐射、热沉、隔热4种形式,但这些传统的热防护结构形式较为单一,不能同时满足防热、隔热和结构承载的需求。目前,热防护结构已经朝着防热、隔热和承载一体化结构方向发展[5]。防隔热一体化结构能够将防热、隔热与承载性能集于一体,充分发挥材料的高温强度潜力,避免飞行器内部遭到高温的侵蚀和损坏[6]。另外,根据高速飞行器的特殊工作要求,轻量化也是热防护结构设计中的关键一环[7-8]。在热防护结构的设计过程中,应尽可能降低研发成本,节省材料,在保证结构的防隔热性能不失效的前提下,减轻结构质量。防隔热一体化结构能够显著提高热防护系统的防隔热效率,降低热防护系统的结构质量,进而减少飞行器的制造和维护成本,增加飞行器的有效载荷。
国内外对一体化热防护结构的研究已很丰富。Bapanapalli等[9]对一体化波纹夹芯板进行了瞬态传热分析,将横截面上的二维传热问题简化为一维传热问题,两种方法得到的结果误差很小,可以显著缩短求解时间,提高计算效率;解维华等[10]通过体积等效法,将横截面上的二维传热问题简化为一维传热问题,两种方法得到的结果温差不超过10 ℃;尹昌平[11]以气凝胶材料作为夹芯层,用缝合-共注射工艺制备承载与防隔热一体化热防护结构,并研究了缝合承力柱对力学性能的影响以及缝合热通道对热传导性能的影响;Kumar 等[12]对一体化褶皱波纹板热防护结构进行研究,开展了具有防热和承载功能的一体化热防护系统的设计;陈立明等[13]提出了一种轻质多层一体化热防护结构方案,使用有限差分法进行求解,进行一维瞬态的传热分析,并使用商业软件ABAQUS 对结果进行验证;李东辉等[14]建立了高温多层隔热结构传热计算模型,对多层隔热结构的瞬态传热及热响应进行数值模拟分析;孙陈诚等[15]以超薄纳米隔热材料为间隔物、金属箔为反射层制备了多层反射纳米隔热材料,并测试其隔热效果。
在防隔热一体化结构中,隔热材料的主要功能是阻止或延缓热量传递给机身结构,保证机身内壁面的最高温度低于结构的许用温度,通常选用轻质、低热导率、低密度材料[16-17],轻质高效的隔热材料对于整个热防护结构来说是至关重要的[18-19]。因此,为了提高热防护结构的防隔热性能,增强结构的耐热性,实现结构的轻量化设计,本文选取SiC气凝胶作为结构中的隔热层,与传统的陶瓷纤维隔热毡相比,SiC 气凝胶的质量更轻,热导率更低,可以耐受1 400 ℃的高温,能够同时兼顾轻质与高效隔热两个条件,是一种理想的高效隔热材料[20-24]。
本文通过建立防隔热一体化模型,采用Crank-Nicolson 方法,分别以SiC 气凝胶和陶瓷纤维隔热毡作为隔热层进行一维瞬态导热分析,对比两种材料在隔热方面的性能优劣。此外,在1 400 ℃极端高温环境以及机体内壁面绝热情况下对SiC气凝胶的隔热性能进行分析,探究SiC气凝胶在不同工况下的隔热能力上限,对结构的防隔热性能进行了评估。进一步对隔热层厚度尺寸进行优化设计,得到在满足结构许用温度条件下隔热层的最小厚度,使结构在质量以及防隔热性能方面达到最佳效果,为热防护结构的优化设计提供依据。
1 模型建立
1.1 物理模型
以高速飞行器外部大面积热防护结构为对象,针对典型多层热防护结构进行传热分析及尺寸优化。该结构从外到内分为防热层、隔热层和机体结构(内壁板冷结构),防热层和隔热层之间、隔热层和机体结构之间分别由磷酸铝和酚醛树脂进行黏结。考虑到大面积热防护结构的主要功能为防止高热流进入飞行器内部引发机体结构和舱内设备失效,且飞行器外壁大面积区域受热相对均匀,因此,该多层热防护结构的传热模型可以简化为沿厚度方向的一维模型。结构的几何模型如图1所示,高温热流直接作用于结构外壁面,机体结构内壁面考虑绝热和对流换热两种边界条件。在建模和计算中,不考虑材料的烧蚀和氧化,各层的黏接界面视为完全接触界面且忽略黏接层厚度。

图1 简化几何模型Fig.1 Simplified geometric model
1.2 材料参数与控制方程
防热层考虑C/C复合材料,隔热层分别考虑陶瓷纤维隔热毡和SiC气凝胶两种材料,机体结构壁板为铝合金。其中,防热层的厚度为8 mm,隔热层的厚度为20 mm,机体结构的厚度为10 mm。SiC 气凝胶的导热系数[25]如表1 所示,结构其余各层材料物性参数[26-27]如表2所示。

表1 密度为9.7 mg/cm3的SiC气凝胶在不同温度下的导热系数Tab.1 Thermal conductivity of SiC aerogel with 9.7 mg/cm3 at different temperatures

表2 各层材料物性参数Tab.2 Physical property parameters of each layer
对表1中的数据进行拟合,拟合曲线如图2所示。SiC气凝胶导热系数λ随温度T变化的函数为

图2 原始数据及拟合曲线Fig.2 Raw data and fitting curve
采用无内热源的瞬态热传导方程:
式中ρ为密度;c为比热;T为温度;t为时间;下标i= 1,2,3分别表示防热、隔热和机体层。对于考虑了导热系数温度相关性的SiC 气凝胶,其热传导方程为
1.3 初始条件与边界条件
1.3.1 初始条件
当t= 0时,视结构为常温,即Ti(x,0)=25 ℃。
1.3.2 边界条件
考虑飞行状态下热防护结构外表面受热条件随时间的变化:
对于机体结构内壁面,当采用绝热边界时:
当考虑内壁面与舱体内部的空气存在自然对流换热时:
式中h为对流换热系数;T|x=L3为内壁面的温度;T∞为舱内环境的温度。
1.3.3 连续条件
各层材料之间忽略接触热阻且考虑完全接触,因此界面处满足温度连续条件和热流连续条件:
2 数值解法与验证
2.1 数值解法
采用有限差分方法中的Crank-Nicolson 方法[28],对控制方程在空间及时间上进行离散处理。Crank-Nicolson 方法对于扩散方程无条件稳定,收敛速度快于古典隐格式和古典显格式,具有更高的精度,并且可以设置更大的时间步长。令Δx为空间步长,Δt为时间步长,对xt平面进行网格剖分,得到初始矩阵的一个长方形网格,如图3所示。
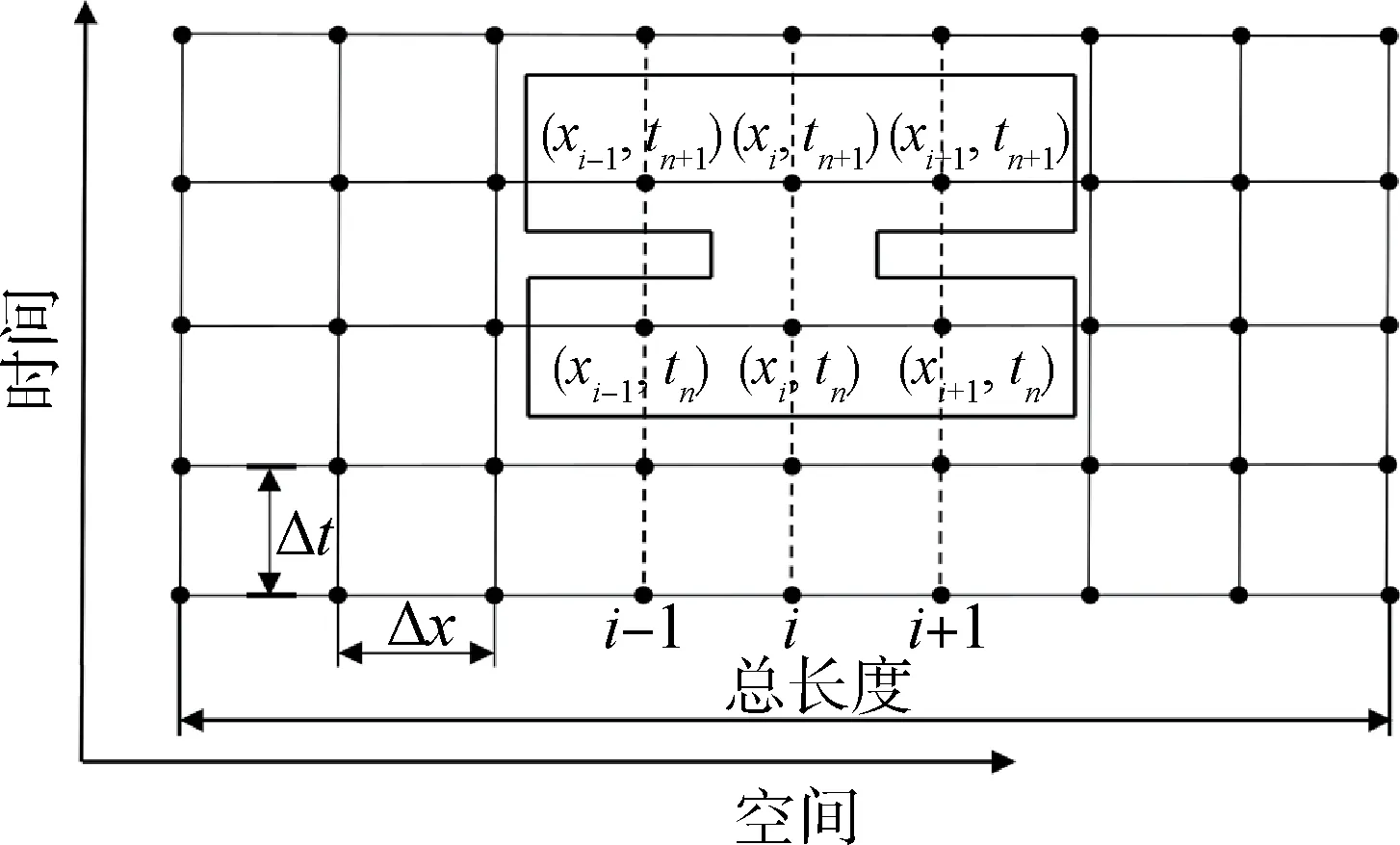
图3 热传导方程的网格划分Fig.3 Meshing of heat conduction equation
可以得到热传导Crank-Nicolson 隐格式的离散方程:
对于各层材料的交界面,根据热流密度的连续条件,对方程左边进行一阶向后差商,对方程右边进行一阶向前差商,则可以得到交界面处的差分格式:
再根据结构内壁面的对流换热边界条件,可得差分格式如下:
内边界条件为绝热时,差分格式为
初始时刻温度为
2.2 模型验证
为了验证本文所建立的传热模型和计算方法的准确性与可行性,本节将验证结果与文献[29]中的盖板式陶瓷热防护系统的有限元分析结果作对比。在使用本文的计算方法时,采用的模型几何参数以及材料物性参数均与文献[29]中的一致。图4为本文数值计算结果和文献有限元计算结果的对比曲线。由曲线可以看出,采用本文数值方法计算得出的结果与该文献有限元计算结果吻合较好。因此,本文的结构模型以及计算方法是可行的,可用于后续防隔热结构的设计分析。

图4 文献[29]与本文计算方法的结果对比曲线Fig.4 The comparison curve between the results of the literature[29] and the calculation method in this paper
3 结果与讨论
3.1 模型整体内部温度分布
对第2 节所建立的模型进行数值求解,选取文献[30]中的再入飞行器温度-时间曲线作为外边界条件,如图5所示。得到的各层材料温度随时间的变化曲线如图6 所示。两种模型中,SiC 气凝胶与陶瓷纤维隔热毡的厚度均为20 mm。

图5 简化的时变温度边界条件Fig.5 The simplified time-dependent temperature boundary condition

图6 两种模型传热性能对比Fig.6 Comparison of heat transfer performance between structures with various insulation materials
由图6a 和图6b 可以直观地看出,两张图中的曲线走势十分相近。在温度载荷持续增加的状态下,随着时间的推移,防热层温度上升的速率比较大,最终在大约500 s时达到最高值,超过了1 100 ℃。由于隔热层的高效隔热作用,隔热层和内壁面的温度变化不大,二者始终保持在200 ℃以下,且上升速率较小。500~1 500 s之间为温度载荷不变的时间段,一直处于1 200 ℃高温,防热层的温度开始保持平衡状态,不再增加,隔热层和内壁面由于一直在吸收防热层传来的热量,二者的温度开始小幅度上升。在1 500 s 之后,温度载荷下降直到结束的时间段,陶瓷纤维隔热毡的温度始终保持在200 ℃以下,而SiC 气凝胶的温度始终保持在100 ℃以下。对比图6a 和图6b 可以看出,500 s 之内二者的温度变化相差不大,这是因为该时间段内温度载荷比较小,且处于逐渐上升的状态。但是在500 s 之后,温度载荷达到了最大值1 200 ℃,结构将处于较长时间的高温冲击,内壁面温度开始快速升高,此时采用陶瓷纤维隔热毡作为隔热层的模型内壁面温度增幅较大,并且在第2 000 s时温度达到了峰值140 ℃。
图6c给出了两种隔热材料对应的内壁面温度变化曲线。采用内壁面温度增幅要明显小于陶瓷纤维隔热毡,并且温度全程不超过80 ℃。在第2 500 s 时外界温度载荷施加完毕,SiC 气凝胶作为隔热层的模型内壁面温度最终约为130 ℃,而陶瓷纤维隔热毡作为隔热层的模型内壁面温度约为62 ℃,二者的差值达到了68 ℃,隔热能力相对提升了大约52%。这表明,SiC 气凝胶的隔热能力要远远优于陶瓷纤维隔热毡的隔热能力,这得益于SiC气凝胶极低的热导率(常温时小于0.03 W/(m·K)),使其在阻碍热量传递方面能够起到主导作用。
3.2 不同工况下机体内壁面温度分布
在上述几个算例中,外边界条件均采用的是图5中的温度-时间变化曲线,温度边界呈现出上升-稳定-下降的趋势,且最高温度不超过1 300 ℃。为了探究结构在极端高温环境下的热防护能力,外边界条件取1 400 ℃恒温。另外,根据高速飞行器的发展需求,要求飞行时间能够达到7 200 s[31],因此外部热源作用时间设置为7 200 s,内边界条件不变,得到的各层材料温度随时间的变化曲线如图7所示。

图7 外边界恒温1 400 ℃时内壁面温度-时间曲线Fig.7 Temperature along time at the inner surface with 1 400 ℃boundary condition
由图7可知,防热层的温度在较短的时间内急剧上升,随后处于稳定状态。隔热层和机体内壁面温度平稳上升,在约3 000 s之后处于稳定状态,温度不再显著增加,保持在200 ℃以下。
图8 为3 种不同工况下的结构内壁面温度变化曲线。当内壁面处于绝热条件下时,由于热量的不断堆积以至于温度始终处于升高状态,最终在2 500 s加热结束时超过了140 ℃。而内壁面在自由对流的情况下热量能够散发出去,温度一直比绝热状态低,并且在第1 800 s 时开始下降,最后在2 500 s 时温度降低至65 ℃以下。这表明若要采用绝热边界条件,那么设计出的隔热层厚度要更大,这也是后续厚度尺寸优化设计的一个上限值。

图8 3种工况下内壁面温度-时间曲线Fig.8 Temperature along time at the inner surface under three different boundary conditions
将绝热边界条件和外边界恒温1 400 ℃两条曲线作对比可以发现,前者最高温为150 ℃,后者最高温为142 ℃,二者仅相差5.6%,因此将绝热条件作为尺寸设计的上限边界条件是合理的。
为了探究不同厚度的隔热层对整体热防护结构防隔热性能的影响,得到隔热层厚度的改变与机体内壁面温度关系的变化规律,下文将分析不同厚度尺寸下SiC 气凝胶与陶瓷纤维隔热毡的隔热性能,在其余各层结构的设计尺寸均不变的情况下,将SiC气凝胶的厚度分别减小50%和65%,对调整后的模型重新进行传热对比分析。图9 为不同厚度的SiC 气凝胶与固定20 mm厚的陶瓷纤维隔热毡传热性能对比曲线。所设计的SiC气凝胶厚度分别为7 mm、10 mm、20 mm。

图9 不同厚度隔热层下内壁面温度-时间曲线Fig.9 Temperature along time at the inner surface with different thicknesses of the insulation materials
由图9可知,当厚度减少到10 mm时,内壁面最高温度升高到了103 ℃,升高的幅度为66%。这表明SiC 气凝胶厚度的变化对于内壁面温度的改变效果非常明显,因此可以在满足内壁面许用温度的前提下,采用减少隔热层的厚度的方法来降低整体结构的质量。陶瓷纤维隔热毡的密度比SiC 气凝胶高出近20倍,相同尺寸下SiC 气凝胶的质量更小,当SiC 气凝胶的厚度减少到7 mm时,在2 500 s的时刻机体内壁面的温度与采用20 mm厚的陶瓷纤维隔热毡的温度相当。这表明若隔热层为陶瓷纤维隔热毡,要想使内壁面温度保持在许用温度范围之内,其厚度必须设计得很大,这无疑会大幅度增加结构的整体质量,不利于飞行器的飞行。若采用SiC气凝胶作为隔热层,其厚度尺寸可以设计得很小,进而减轻结构整体质量,满足飞行器在保证不受破坏的前提下设计最轻质量的原则。
3.3 隔热层结构尺寸优化设计
3.3.1 优化模型
针对多层热防护结构,以隔热层SiC气凝胶的最小厚度尺寸为优化目标,以机体内壁面温度不超过某一定值为约束条件,在其余结构尺寸不变的情况下,进行热防护结构单变量优化设计。
a)目标函数。
结构外部的温度载荷设置为恒温1 400 ℃持续工作3 600 s,内壁面边界条件为自由对流换热,高温下SiC 气凝胶的导热系数取常数0.04。设隔热层的厚度为L2,因此优化目标为SiC气凝胶的厚度最小值:
b)约束条件。
本节对热防护结构进行优化设计时仅考虑温度载荷以及由此产生的结构热效应,确保工作时间为3 600 s 时机体内壁面的温度不超过150 ℃,且超过100 ℃的时间不超过5 min。这样的约束条件可以充分保护舱体内部的仪器不会受到高温的破坏,因此约束条件的数学描述为
3.3.2 优化分析
使用MATLAB 编写程序,为了缩小范围,先在限定区间内进行步长为1 mm 的定步长初次遍历。随后利用二分法进行最优点的查找。具体算法步骤如下:
a)步骤1:令d=dmin,求出温度分布T1(x,t),若满足第3.3.1节的约束条件则结束,否则转步骤2;
b)步骤2:令d=dmax,求出温度分布T2(x,t),若满足第3.3.1节的约束条件则结束,否则转步骤3;
c)步骤3:若dmax-dmin<ε,则结束,否则转步骤4;
d)步骤4:令Δd=(dmin+dmax)/2,求出温度分布T3(x,t),若满足约束条件,则dmax= Δd,不满足则令dmin= Δd,转步骤3。
经过迭代求解后,得到如图10 所示的内壁面的最高温度与隔热层厚度的关系变化曲线。结构外部的温度载荷状态设置为持续3 600 s的恒温1 400 ℃。

图10 最高内壁面温度与隔热层厚度关系Fig.10 Relationship between maximum temperature of inner surface and insulation thickness
由图10 可知,内壁面的最高温度随着隔热层厚度的增加呈现出单调递减的趋势,并且在0~20 mm厚度区间内下降较快,说明SiC气凝胶即使在较小的厚度尺寸下依然具有较强的隔热能力,对结构的防隔热性能影响较大,厚度的小幅度改变都会对内壁面温度造成很大影响。在SiC 气凝胶的厚度尺寸大于20 mm之后,其厚度的增加对于内壁面最高温度的影响越来越小,表明在第1 个约束条件下继续分析SiC 气凝胶的厚度已经意义不大。当SiC 气凝胶的厚度为23 mm时,内壁面的最高温度为150 ℃,满足第1 个约束条件,因此SiC 气凝胶最小厚度的第1 个充分不必要条件为[L2]1≥23 mm。
利用同样的方法得到如图11所示的内壁面温度超过100 ℃的时长与SiC 气凝胶厚度的关系变化曲线。由图11 可以看出,当SiC 气凝胶的厚度为39.6 mm时,内壁面温度低于100 ℃的时间为300 s,满足第2个约束条件。而厚度在大于39.6 mm之后内壁面温度低于100 ℃的时间始终小于300 s,表明在此之后继续增加SiC 气凝胶的厚度对结构防隔热性能影响不大。因此SiC 气凝胶最小厚度的第2 个充分不必要条件为[L2]2≥39.6 mm。与第一个约束条件[L2]1≥23 mm 取区间交集,可得SiC气凝胶的最小厚度为39.6 mm。
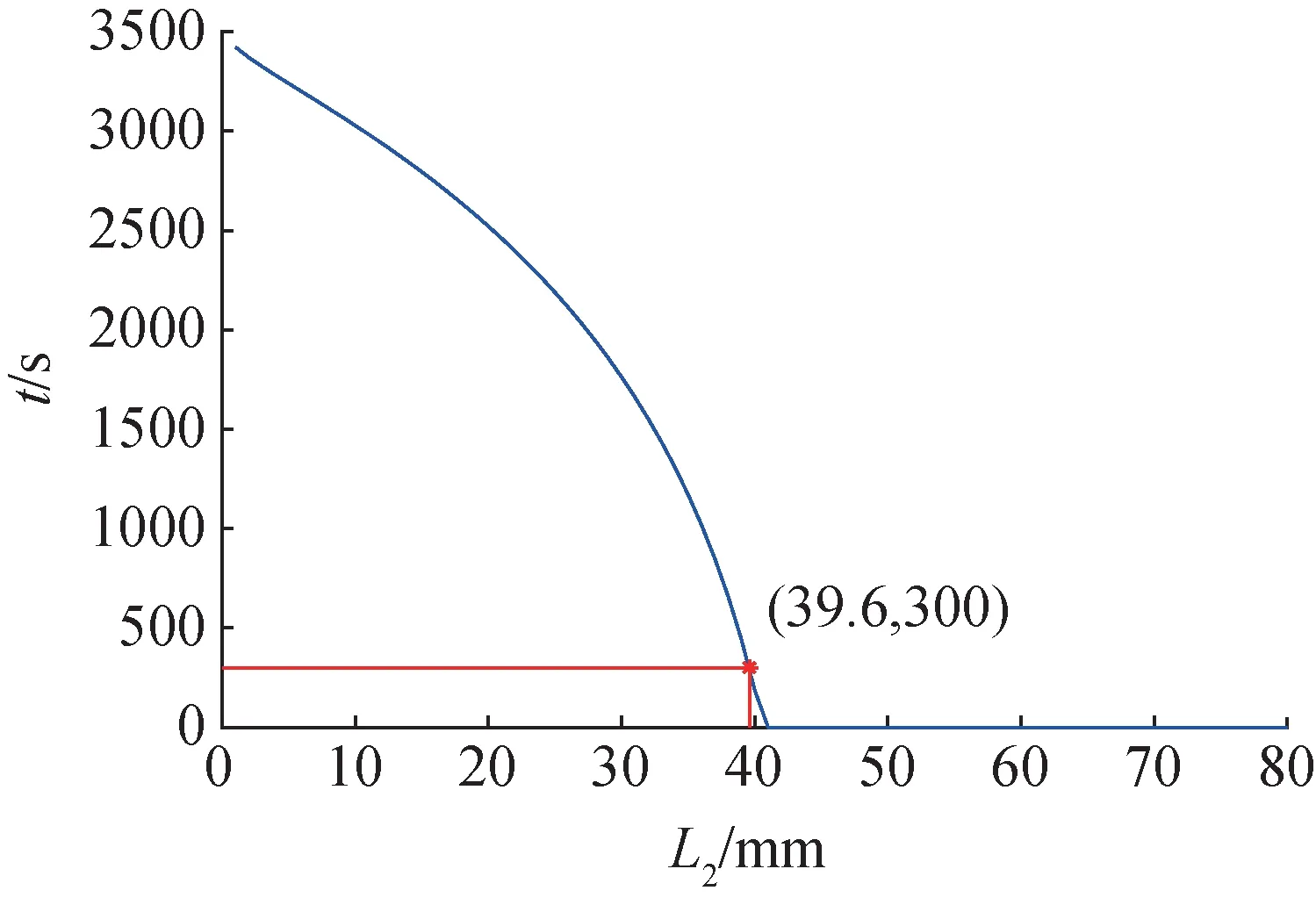
图11 内壁面温度超过100 ℃时长与隔热层厚度关系Fig.11 The relationship between the length of insulation layer and the temperature of inner surface over 100 ℃
取SiC气凝胶厚度L2=40 mm,此时内壁面温度随时间的变化如图12所示。
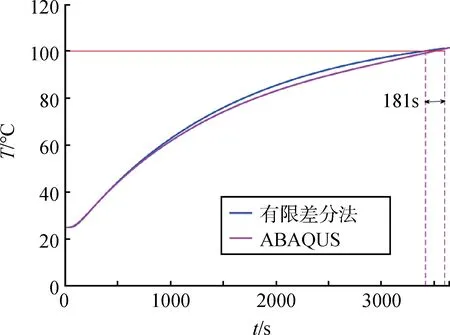
图12 内壁面温度变化情况(L2=40 mm)Fig.12 Temperature change of inner surface (L2=40 mm)
由图12 可知,内壁面温度超过100 ℃的时长为181 s,短于5 min,温度的最大值也小于150 ℃,满足两个约束条件。该结果也与ABAQUS 有限元分析进行了对比验证,两条曲线非常吻合,证明了优化设计和数值解法的准确性。
4 结 论
本文针对以SiC气凝胶作为隔热层的多层热防护结构,考虑材料导热系数的温度相关性,建立了热防护结构厚度方向的传热分析模型。利用Crank-Nicolson 方法计算了整体结构在不同工况下的温度场分布,分析其防隔热性能以及传热机制,并将采用不同隔热材料的多层热防护结构隔热性能进行了对比,在满足约束条件的前提下对SiC气凝胶隔热层的厚度进行了优化设计,获得如下结论:
a)在简化的高速飞行热环境条件下,使用SiC气凝胶作为隔热层时结构内壁面的温度要比使用陶瓷纤维隔热毡作为隔热层低50 ℃,且温度全程不超过100 ℃,同一结构厚度下隔热能力相对提升了约40%。
b)在热边界条件为1 400 ℃恒温和结构内壁面绝热两种极端的情况下,68 mm 厚的结构内壁面温度始终保持在150 ℃以内。将不同厚度的SiC 气凝胶与陶瓷纤维隔热毡的计算结果作对比,当SiC气凝胶的厚度减少到7 mm 时,机体内壁面的温度与采用20 mm 陶瓷纤维隔热毡的温度相当,但厚度降低了65%。
c)对SiC气凝胶的厚度尺寸进行优化,在满足内壁面温度不超过150 ℃且超过100 ℃的时间不超过300 s两个约束条件下结构的最优厚度为39.6 mm,并将其与有限元分析结果进行了对比验证,证明了厚度优化设计的数值解法的准确性。

