无人机集群分层通信及连通性研究

刘 峰，王振亚，吴志壕，路 鹰

（中国运载火箭技术研究院，北京，100076）

0 引 言

无人机集群（Unmanned Aerial Vehicles Cluster，UAV Cluster）在执行各种复杂任务的过程中，依赖于队形的保持与变换，需要通过集群中相互通信交换信息来实现，集群编队的导航、控制［1-8］、通信等一直是国内外研究的热点。单个无人机通过卫星导航可以确定自身的位置，彼此之间通过通信交换位置等信息，可以保持队形避免碰撞、变换队形完成任务。在强干扰等复杂对抗环境中，采用窄波束定向发射的电磁信号进行通信时，由于无法预先确定信号接收方的位置，需要对无人机集群满足通信要求的构型开展研究［9］。

本文提出一种无人机集群分层通信的方式，通过连通性算法判断上下两群无人机是否通过两两之间的双向通信，形成一个完整的连通性网络，实现集群中通过多架无人机的接力传递实现信号在集群中的扩散，从而实现任意两架无人机之间的通信。

1 无人机集群

1.1 集群的生成方法

为完成区域搜索、定点监视等任务，无人机集群沿预先规划的航路点时间序列飞行。无人机集群分为上下两层，两层之间的高度差相对固定，并由通信模块的信号覆盖能力确定，属于同一层的无人机的高度相同，且在执行任务的过程中一直保持基本恒定的高度和相对稳定的姿态。无人机集群如图1所示。

图1 无人机集群Fig.1 UAV cluster

1.2 集群通信方式

针对上下分层的两群无人机，采用视锥型双向通信模块，零姿态时，上层无人机通信模块朝向正下，下层无人机通信模块朝向正上。上层无人机之间以及下层无人机之间不存在通信联系。只有上层无人机与下层无人机之间可以通信。通信模块可以同时接收多路信号，信号收发互不干扰，不考虑空间信号的衰减和背景杂波的干扰。

为了支撑特定任务的完成，集群中的无人机需要交换各自从外部获取的信息和自身导航定位的信息，上层单个无人机通信发射的单元信号一般无法完整覆盖下层所有无人机。下层对上层亦存在同样问题，集群中任意两架无人机间的信息交换，需要多架无人机的中转才能实现。无人机间的信息中转不是简单的转发，需根据任务的特点对多路信息进行合并与重组。

为了满足路径规避、绕行障碍物等要求，各无人机之间的相对位置会发生变化，通信路径、连通性及通信拓扑网络随之变化。接力通信中，当两架无人机之间存在多条通信路径时，同时接收多路信息并通过合并重组消除其中的冗余信息。

对于执行同一任务的无人机集群，其上下两层分别为nUp和nDn架，设定各自的标称巡航高度分别为HUp和HDn，单位为m；飞行中的上下两层无人机均匀散布在以同一时间序列下的航路点为中心、分别以rUp和rDn为半径的区域内。确保正常通信时，通信模块的视锥发射覆盖半角为θ0，其有效斜距为d0。

在当地大地直角坐标系下，设上层无人机的坐标为Ui=（xUP，iyUP，izUP，i）T、下层无人机的坐标为Dj=（xDn，j yDn，jzDn，j）T，其中i=1， 2， … ，nUp，j=1， 2， … ，nDn，设单位矢量Z-=(0 0 -1)T，则有：

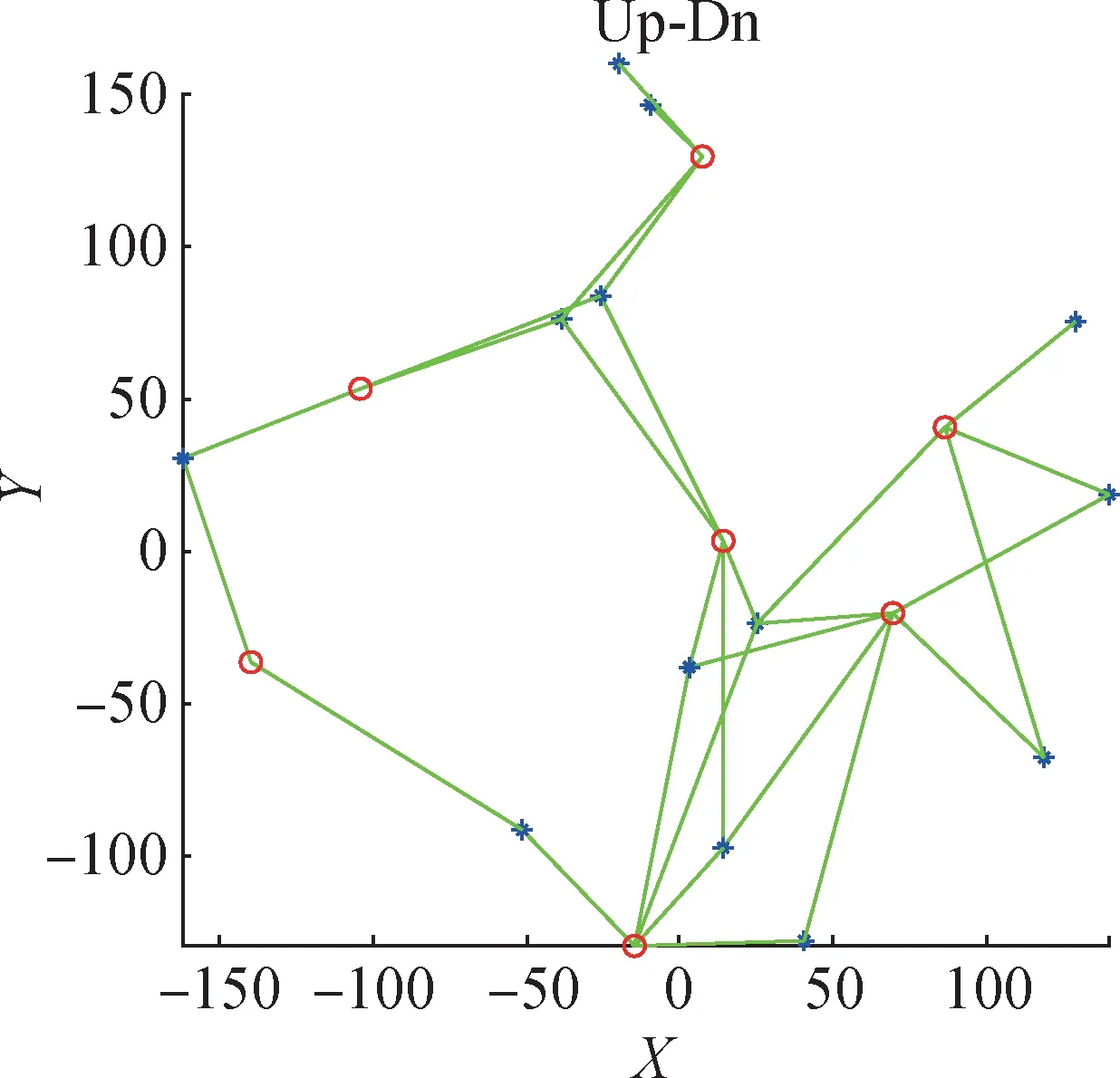
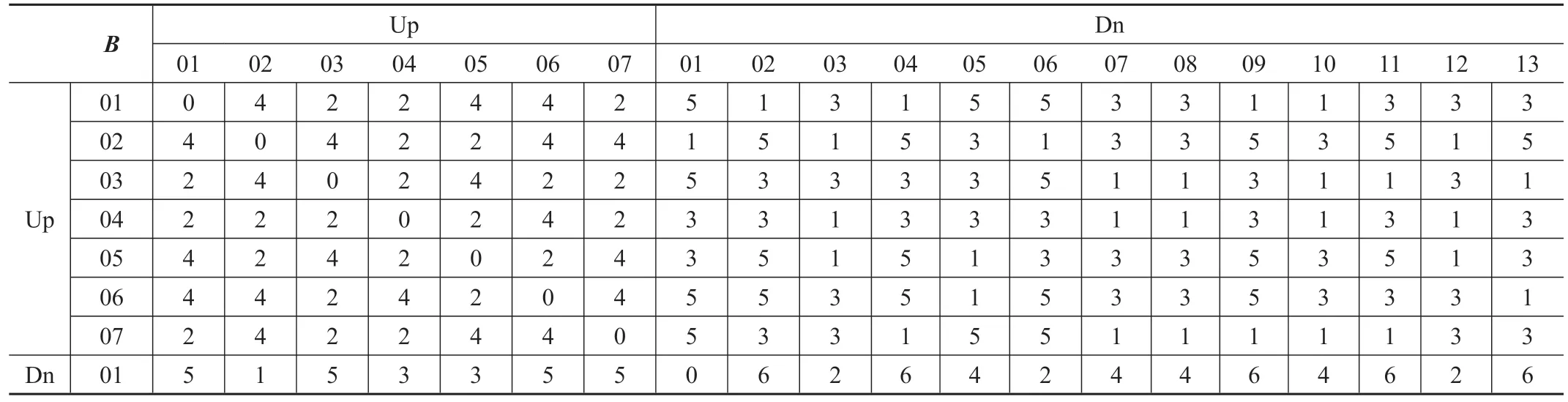
当θij<θ0且dij

1.3 集群的连通性

为了在集群中通过多架无人机中转实现任意两架无人机交换信息的机制，重点开展无人机集群拓扑构型的连通性判断和通信路径研究。

构建通信关系矩阵：

式中aij= 1表示上层无人机Ui与下层无人机Dj建立了直接的双向通信联系，否则aij= 0。遍历上层无人机Ui与下层无人机Dj的所有组合，得到通信关系矩阵A。构建通信路径最小长度矩阵：

将上层无人机靠前、下层无人机靠后排成一列，其中，bij≥0 表示第i号无人机与第j号无人机的信息最少通过bij次接力传递实现通信，且当i=j时bij= 0；两架无人机的通信存在对称性，即BT=B，bij=bji。

取bMax=nUD×nUD作为bij的初始值，在完成通信路径最小长度矩阵的构建后，若∀i，j∈[1，nUD]，i≠j均有0

用bMax初始化B阵后，构建B阵的步骤如下：

a）第1 步：遍历A阵，当aij≠0 时，置bi，j+nUp=bj+nUp，i=aij。

b）第2步：多次循环遍历B阵，若存在bij=bMax，则跳到第3 步；当所有0 ≤bij

c）第3步：遍历中，对于i，j∈[1，nUD]，i≠j，若bij=bMax，则跳到第4 步；否则继续遍历B阵，遍历完本轮次，则跳到第2步。

d）第4 步：遍历k∈[1，nUD]，k≠i，k≠j，当0

1.4 算法的有效性

根据连通性计算方法的特性，其运算时间与无人机集群规模的平方成正比，和无人机之间最大接力通信次数成正比，而无人机之间最大接力通信次数由集群的几何构型决定，一般呈一字长蛇形分布的次数最大，呈近似圆盘内均匀分布的次数较小。初步仿真计算可知，100架以内的无人机集群在1 s内可完成连通性判断，说明算法在运算时间上是有效的。

根据任务需要，无人机之间的相对位置关系一直处于动态变化过程中，为集群设定航迹的时间序列，所有无人机共同跟踪，同时为无人机之间设置防碰撞的最小距离和通信连通的最大距离，上下两层的无人机集群聚集后即可计算连通性，说明算法在集群动态变化上是有效的。

1.5 实践的可行性

根据连通性计算方法的有效性，上下分层、中心位置同步、保持基本恒定高度和相对稳定姿态的小规模无人机集群一定可以实时计算通信路径的连通性。

工程实践中，有毁伤的条件下只考虑有效的无人机。对上下各层，以无人机为节点、以相邻两无人机之间的连线为边，基于钝角最小三角形对集群进行剖分，确定当前无人机的所有相邻无人机，使其所有的间距保持在防碰撞的最小距离和通信连通的最大距离之间，自动形成满足连通性的无人机集群，说明算法在实用上是可行的。

2 算例分析

在大地水平坐标系内，在两个无人机集群位置关系上，上层无人机共7架，飞行高度为（800±10）m，均匀分布在直径为320 m的区域内；下层无人机共13架，飞行高度为（600±10）m，均匀分布在直径为360 m 的区域内。nUD共计20 架无人机，相应的bMax=20×20=400。

正常通信时，通信模块的视锥的发射覆盖半角为30°，其有效斜距为300 m，其垂直距离200 m的覆盖区域直径为145.6 m。

集群分层立体及平面示意分别如图2、图3所示，所有通信关系如表1所示。

表1 集群分层之间的通信关系Tab.1 Communication relationship between cluster layers

图2 集群分层立体示意Fig.2 3D illastrate of cluster layering

图3 集群分层平面示意Fig.3 2D illastrate of cluster layering

通过无人机集群拓扑构型的连通性判断和通信路径长度计算，得到通信路径最小长度矩阵如表2所示。表2中B阵的所有数据满足0 ≤bij

表2 集群之间通信路径的最短长度Tab.2 Shortest length of communication path between cluster layers

3 结束语

本文提出一种无人机集群分层通信与连通性判断的方法，可用于使用抗干扰型窄波束固定安装的低成本通信模块的无人机集群实现整体数据共享。该方法除满足事前航路规划、上下分层拉开距离、保持两层几何中心重叠等基本要求外，无须为通信指向配置云台，无须指示通信目标的位置。分层通信的无人机集群具备去中心化与相互冗余备份等优势，是完成高风险、高难度等复杂任务的理想选择。

高风险对抗环境中难免出现无人机损伤，通信网络存在冗余路径，有利于在个别无人机失效时，采用等距策略微调相对位置仍然保持集群的连通性，提升了无人机集群通信的抗毁伤能力。后续在无人机的飞行策略上，通过制定合适的绕飞轨迹，可以在主要无人机集群附近建立适当的探索区域，上下两层均派出无人机暂时脱离主集群到周边巡视，将落单的无人机拉入主集群，同时派出无人机也可自行安全回归主集群，根据任务需要使集群的分群与合并成为可能。