城市地价空间非平稳格局与测度技术优化应用探索

邢 琦，陆 颖，王 健，3

（1.中国农业大学土地科学与技术学院，北京 100193；2.中国国土勘测规划院，北京 100035；3.中国土地政策与法律研究中心，北京 100193）

城市地价作为土地市场运行的重要反馈指标，引导城市产业发展的布局，在塑造城市形态和经济结构方面发挥着关键作用[1]。城市地价的空间格局及其决定因素一直受到学术界的关注。供求机制、属性特征、空间效应三方面是当前城市地价空间格局研究的主流，主流观点认为地价受土地利用政策、城市功能区划等宏观因素[2-3]和区位、邻里、个别等微观要素的共同作用[4-5]。城市的发展和区域空间关系的复杂性对城市地价格局和决定因素的识别测度带来了重大的挑战，各类要素空间发展的不均衡引导地价出现非平稳的空间格局。探究地价空间非平稳格局对引导城市地价与产业经济协调发展，实现城市空间资源精细化管理和配置具有重要的指导意义。因此，地价空间非平稳格局研究也是当前城市地价研究探索的主流方向，其研究的主要核心是测度模型构建。

特征价格模型[5]、空间计量模型[6-7]等方法在一般意义上被广泛用来研究城市地价空间格局及其决定因素，但这些方法存在先天性不足。如流行的标准特征价格模型将各影响因素的边际效应视为固定常数，没有考虑地价的空间依赖性，导致参数估价的偏差和不一致问题[8-9]。为此，研究者引入空间滞后模型（SLM）、空间误差模型（SER）、空间杜宾模型（SDM）等空间计量模型解释地价的空间依赖性。然而，在城市空间动态发展中，空间要素禀赋及其集聚形态的差异，会进一步导致地价与其属性特征间表现出非线性的空间效应。因地理区位的差异，各驱动因子对地价的作用结构呈现明显的空间异质效应，空间计量模型的线性假设使其本质上无法测度这一异质性。为此，地理加权回归（GWR）、变异系数模型（VCM）等模型被诸多学者采用来量化属性特征因子对地价空间格局的异质性影响。顾此失彼，此类模型未将空间自相关参数嵌入回归项，地价空间依赖性强度的动态变化又被排斥在模型测度之外。因此，如何科学测度和反映依赖性与异质性的共同效应，是当前模型构建和测算的难题。

地价与相关因子间的空间关系受到区域空间系统的综合作用，表现出空间依赖性与异质性两大特征同时存在，且两者均具有非平稳性的事实[10-11]。既有常用模型中的“非平稳”关注的是空间异质性，例如，公共基础设施条件的差异导致地价空间分布的不均衡，但少有考虑空间依赖强度的动态变化，例如，相邻地域间地价存在相互作用，且作用强度随时空变化。未在模型中考虑两类空间特征参数均随空间而变化的特征，就难以准确地反映日趋复杂的城市土地利用空间格局与价格形成机制。因此，需要探索一个综合性模型，该模型可以同时将空间自相关和空间异质性参数嵌入空间变化系数，进而测度识别城市地价的空间非平稳特征及其驱动机制。学者们不断尝试提出包含空间自相关和空间异质性的模型框架。例如，CHO 等提出了一种结合地理加权回归（GWR）和空间误差模型（SEM）的GWR-SEM 模型[12]；BASILE等提出具有空间自相关的地理加法模型的扩展，允许考虑空间自相关的误差项和内生变量[13]。但这些模型存在两个明显的缺点：一是未考虑空间参数异构情况（即部分参数在空间上恒定，而另外一些则是变化的），模型灵活度较低导致估计性能不佳；二是没有较好地解决多重共线性的问题，可能导致估计参数值波动甚至出现符号反常的现象[14]。为解决此问题，GENIAUX等[14]尝试提出一类新的数据生成过程（DGP），称为多尺度地理加权回归—空间自回归模型（Multiscale Geographic Weighted Regression-Spatial Autoregressive model,MGWR-SAR）。MGWR-SAR模型中的回归参数和空间自相关系数可以随空间变化[14]。GENIAUX 等通过深入的蒙特卡罗分析，评估既有经典模型与其提出的异构系数模型的性能，证实所提出的MGWRSAR模型具有良好的空间估计效果[14]。

当前国内鲜有MGWR-SAR 模型的应用与研究，从既有的海外学者将其应用到城市住房市场[15-16]、区域创新活动[17]、劳动力参与率[18]等领域的研究上看，该模型能有效处理空间依赖性和异质性具有非平稳特征的问题。MGWR-SAR模型放松了关于空间相互作用性质的假设，将其应用于测度城市地价空间非平稳性也具有较强的可能性。本文在明确城市地价空间非平稳格局形成机制的基础上，以某一城市商服用地地价数据分析作为案例，应用新的空间测度技术重新考察我国地价的空间形态，实证检验MGWR-SAR模型相较于传统空间计量模型的性能效果，以期为地价空间测度提供新的技术参考，也为其他地理要素空间研究提供方法借鉴。

1 城市地价空间的非平稳格局

经济活动收益使城市土地功能定位、利用方式及强度产生异质性，进而出现土地利用的空间差异。屠能、韦伯、艾萨德、克里斯塔勒等学者构建的经济区位论表明，区位会影响城市经济活动的潜在收益，进而导致地价的差异。可以说，城市地价是土地区位条件优劣差异的结果[19]。进一步，我们可以从区位的绝对性与相对性两个视角来认识区位。绝对区位是指土地某一功能在空间上的自然地理承载位置；相对区位是指土地某一功能与其他空间要素功能的相互关系的空间关联。绝对区位的固定性引导地理邻近地区间地价存在空间依赖性，而相对区位的不均衡是地价存在空间异质性的主要原因。空间依赖性和空间异质性的非线性变化共同形成地价空间格局的非平稳特征。

1.1 绝对区位与地价的空间依赖性

土地空间位置的固定性决定了其绝对区位不会发生转移。地理学第一定律提出，地理邻近的事物间存在关联性[20]。绝对区位决定了每一寸土地空间都是唯一的，土地市场会存在瑕疵，因为供给具有一定的“垄断性”，价格“依赖于”地块区位。此外，土地最终交易价格不仅取决于自身属性特征，还依赖于买卖双方的行为及心理预期等[21]。在从众心理的引导下，买卖双方会依赖具有类似特征的邻近土地的历史价格信息[22-23]。原因在于地理邻近地区的土地往往具有相似的外部环境特征，其土地的价值也通常可以预示或引导着附近地区的地价预期[24]，即相近的地理事物在空间上互为关联的定律也引导着地价具有空间依赖性。

1.2 相对区位与地价的空间异质性

相对性是一个动态的概念，因此，土地相对区位受城市空间发展的影响处于一个动态变化的过程。在城市扩张和城市功能升级过程中，城市空间系统要素会发生动态变化，具体表现为城市交通、城市功能区（如商业集聚区）、公共基础设施等城市空间实体的发展和改变[25]。空间实体的变化会导致土地相对区位优劣程度发生改变，带来土地空间区位的不均衡，影响用地需求者的支付意愿，导致地价的空间分异[26]。城市内部空间要素的禀赋特征和集聚形态的空间异质性引导地价空间分异格局的形成，而且不同形态的空间要素会对地价产生差异化的空间效应。从空间要素的形态表征来看，地价驱动因子可抽象为点状、线状和面状因素[25]。点状因素如商业中心、金融网点等，类似“增长极”，对周围受力场的地价产生辐射影响，表现为周围地价随着距“增长极”距离的增加而衰减；线状因素主要指公共交通设施等，对周边地价存在“廊道效应”，表现为距“廊道”外侧距离的增加，地价呈现递减趋势；面状因素如绿地覆盖度、环境污染度等由要素中心呈同心圆波纹状向外辐射，地价随着距要素中心距离的增加而衰减。不同形态的空间要素集聚产生差异化的空间效应，传导形成地价空间异质性格局。

1.3 空间依赖性与异质性的综合效应

地价不仅受自身土地属性特征的影响，还受到其他空间地价的影响[27]。土地自身属性特征的异质性导致地价空间分布的不均衡，表现为空间异质性。空间距离会影响地价信息交互和传递的有效性，地价的外溢效应会随空间距离的增加而衰减[28]。地价受其他空间地价的影响强度会发生动态变化，表现为空间依赖强度的非平稳性。地价空间依赖性的非线性与空间异质性综合作用形成非平稳的地价空间格局（图1）。

图1 城市地价空间非平稳格局的形成机制Fig.1 Formation mechanism of spatial non-stationary pattern of urban land price

2 城市地价空间非平稳性的测度模型技术比较

空间依赖性建模测度领域，学者通常应用空间滞后模型、自变量空间滞后模型、空间误差模型和空间杜宾模型及其组合模型进行研究[29]。空间异质性建模测度领域，学者通常应用地理加权回归或多尺度地理加权模型等进行研究[30]。常见的空间滞后模型、空间杜宾模型参数的线性假设使得其难以捕捉地价空间异质性。同时，既有研究多采用地理加权回归或多尺度地理加权模型解释土地自身属性对地价的异质性影响，但未考虑相邻空间地价对本区域地价的影响。模型未将空间自相关参数嵌入回归项，空间依赖性强度的动态变化又被排斥在模型测度之外。

因此，需要一个综合性模型能够解释地价空间依赖性和异质性两大特性非平稳并存的特征，特别是关注空间依赖性的非线性变化。而解释非平稳并存特征需要模型同时将空间自相关参数项和空间异质性参数项嵌入空间变化系数。MGWR-SAR模型考虑空间参数异构的情况，即回归参数和空间自相关系数可以随空间变化而变化。这一性质使该模型能更好地解释地价空间依赖性和异质性两大特性非平稳并存的特征。基于此，本文探索将MGWR-SAR 模型首次应用于国内地价空间非平稳性测度研究，改进当前常用的地价估计方法及模型，实证检验MGWR-SAR模型相较于传统空间计量模型的性能效果。

2.1 空间计量模型

空间计量模型的一般形式如下：

式（1）中：Y为城市地价；W为空间权重矩阵；X为驱动因子；μ为随机误差项；β为驱动因子对地价的影响；λ为相邻地区地价对本地区地价的影响；δ为相邻地区驱动因子对本地区地价的影响；ρ为随机误差项的空间相关系数；ε为误差项。当δ=ρ=0时，本式为空间滞后模型，当λ=δ=0时，本式为空间误差模型；当ρ=0时，本式为空间杜宾模型。根据LR 检验（Lagrange Multiplier Test）结果判断使用空间计量模型的类型。

2.2 多尺度地理加权回归模型（MGWR）

式（2）中：Yi为城市土地样点i的地价；（ui，vi）为第i个地价样点的空间坐标；j为驱动因子个数；Xij为第j个驱动因子在第i个样点处的观测值；αj为全局变量的回归系数，又称常系数；βj为局域变量j的回归系数，又称变系数；n为全局变量个数；m是局部变量个数，j=n+m；εi为随机误差项。

2.3 多尺度地理加权回归—空间自回归模型（MGWRSAR）

GENIAUX等研究引入了一类新的数据生成过程（DGP），称为MGWR-SAR 模型（多尺度地理加权回归—空间自回归模型）。MGWR-SAR模型考虑了回归参数和空间自相关系数存在空间平稳的和/或非平稳的可能性。模型的一般形式如下：

式（3）中：Y为城市地价；（ui，vi）为第i个地价样点的空间坐标；h是带宽参数，可基于给定的距离核函数来定义每个地价样点i坐标（ui，vi）周围的局部子样本数；λ为相邻地区地价对本地区地价的影响，λ的值取决于坐标（ui，vi），即λ=λ（ui，vi；h）；W为空间权重矩阵。Xc为常系数驱动因子，即全局变量；βc是常系数驱动因子的系数值；Xv为变系数驱动因子，即局域变量；βv是变系数驱动因子的系数值；βv的值取决于坐标（ui，vi），即βv=βv（ui，vi；h）；εi为随机误差项；kc是常系数驱动因子的个数；kv是变系数驱动因子的个数，总驱动因子个数k=kc+kv。

GENIAUX等将式（3）中参数λ、βc、βv进行空间固定和变化组合，得到9个不同的DGPs模型：

上述各式中变量含义与式（3）相同。

为了选择合适的模型，第一阶段假设所有参数（包括空间自回归项）均具有空间非平稳性。然后，进行空间变异的蒙特卡罗检验，结合枚举法得到的各模型的评估指标值（残差平方和、均方根误差和AIC值）识别是否存在全局变量。在获取全局变量和局部变量的信息后，选择适当的模型进行估计。本文采用了双方核函数和自适应带宽，考虑到局部子样本重叠会人为地增加值。因此，本文将采用调整后的估计显著性水平。本模型采用GENIAUX 等[14]发布的名为mgwrsar的R包测算实现①mgwrsar:GWR and MGWR with Spatial Autocorrelation version 1.0 from CRAN（rdrr.io）。。

3 实证研究

3.1 数据来源与变量设定

3.1.1 地价数据

本文以我国浙江省宁波市城六区商服用地为研究案例②以浙江省宁波市为案例的考虑主要有三：一是我国东部沿海地区的城市产业发展市场化程度较高，土地价格的市场化配置机制较为活跃，地价在城市空间上显示的特征更为明显；二是宁波市的城市格局和经济行为在空间形成上，区位竞价较为成熟，邻里特征明显；三是数据得可获得性和数据的准确性。本文以宁波市为例，对方法的探索能够应用到其他城市。，所采用的宁波市城六区商服用地地价数据来源于中国土地市场网③https://www.landchina.com/#/。，包括2017—2022年宁波市城六区167 宗出让地块所处区域、土地级别、土地面积、规划容积率、建筑面积、建筑密度、出让方式、成交价格、用地类型等信息。为满足研究需要，对该数据进一步处理。首先，剔除出让价格存在异常的样本数据；其次，对样本地价进行交易期日修正、容积率及特殊情况修正，确保样本地价的可比性④考虑到加油加气站用地属于特许经营的特殊商服用地，出让溢价率较高，因此，研究中剔除加油加气站用地样本。交易日期统一修正至2022年第四季度。。最终确定147宗有效样本数据。样本平均出让面积16 244.16 m2，覆盖宁波市全部6个辖区、8个土地级别，可以代表宁波市城六区商服用地地价整体情况。

3.1.2 地价驱动因子选取

商服用地的地价受宏观影响因素和区位、邻里和个别等微观影响因素的综合作用影响[31-34]。借鉴既有商业用地价格的研究实践[1,34-35]，并通过多重共线性检验和逐步回归剔除部分共线因素和对地价贡献较小的因素，最终选取12 项指标（表1）。（1）宏观影响因素。包括土地利用制度与政策、城市规划、税收等一般性影响因素[36-38]。本文采用土地距特殊用途区的距离，衡量不同类型城镇开发边界对地价的指导和约束作用。（2）区位因素。主要指市场、交通、技术等社会经济因素，包括区位中心性因子、城市交通因子和集聚因子等[1,39]。本文采用商服潜力、公共交通便捷度和对外交通便捷度衡量土地的区位条件。（3）邻里因素。经济学中的邻里因素包括社会经济结构条件[40]、公共基础设施条件[41]、外部环境条件[42]等。影响商服用地地价的邻里因素集中于后两项。本文选取金融网点、停车场、公园三类基础设施的分布衡量商服用地周围公共基础设施条件；选取绿地覆盖度衡量商服用地周围环境条件。（4）自身因素。自身因素主要是指由于地块本身条件的变化而影响土地价格的因素，如地块的形状面积、容积率、临街状况等[43]。本文选取规划容积率衡量商服用地的个别因素条件。

表1 商服用地地价空间非平稳性的驱动因子指标体系Tab.1 Index system of driving factors for spatial non-stationarity of commercial land price

3.2 结果分析

3.2.1 地价空间相关性与异质性

为了检验地价是否具有空间属性，对地价样本进行Q-Qplot检验、空间相关性检验。Q-Qplot检验结果表明，将商服用地地价数据进行对数转换后，地价数据基本符合正态分布，可用于进一步的空间分析。根据探索性空间分析方法计算得到商服用地地价的指数显著为0.173，这表明宁波市商服用地地价存在显著的空间依赖性。LMI 散点图（图2）结果表明，中心城区商服用地地价存在明显的高值集聚，而低值集聚区主要分布在奉化区的北部；从地价全局趋势图来看，地价在东西和南北方向均呈现倒“U”型分布（图3），这也表明地价存在一定的空间异质性。

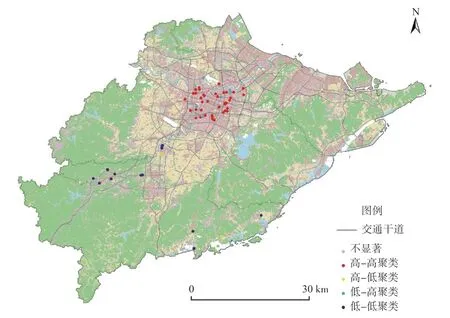
图2 宁波市商服用地地价的LMI散点图Fig.2 LMI scatter plot of commercial land price in Ningbo

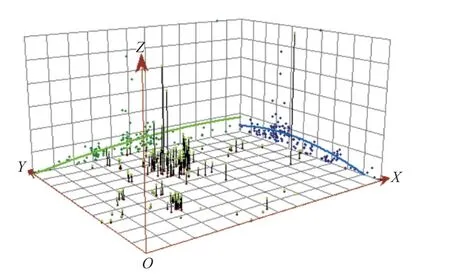
图3 宁波市商服用地地价的全局趋势分析图Fig.3 Global trend analysis of commercial land price in Ningbo

构建LM检验进行空间相关性检验，检验结果LM no lag和LM no error两个统计量分别在1%和5%的水平下拒绝了原假设（LM no lag=7.994 8，LM no error=2.928 7），R-LM no lag统计量在1%的水平下拒绝了原假设（R-LM no lag=5.749 4，R-LM no error=0.683 3），表明应该选用空间滞后模型进行估计。所有变量的方差膨胀因子（VIF）的都小于10，表明变量间不存在多重共线性的问题。空间滞后模型和MGWR 模型的估计结果见表2。

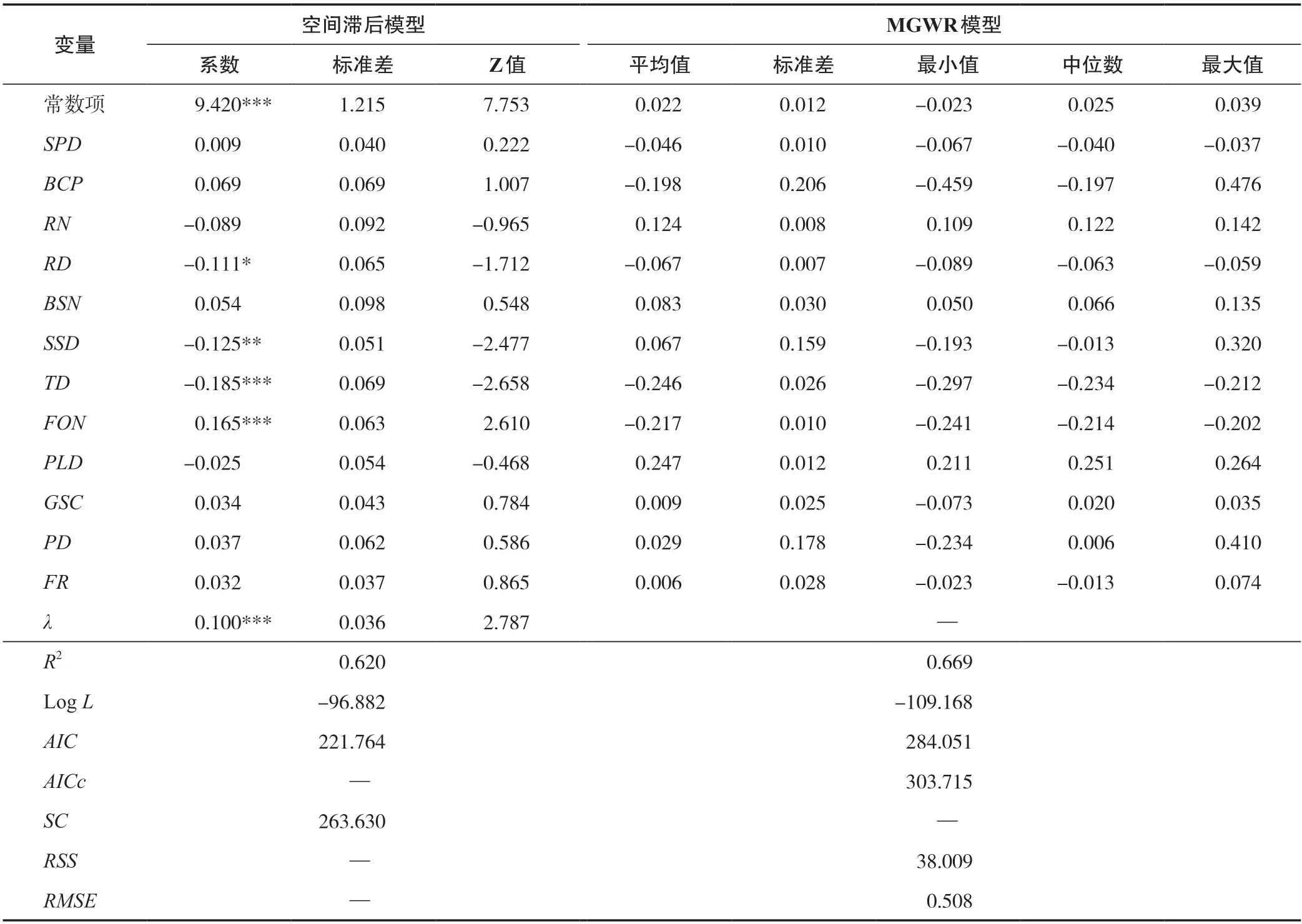
表2 空间滞后模型及MGWR模型的估计结果Tab.2 Estimation results of Spatial Lag Model and MGWR model

在空间滞后模型（表2）中，空间自相关系数在1%的水平下显著为正，说明宁波市商服用地地价存在显著的空间溢出效应。在MGWR模型（表2）中，通过各变量回归系数平均值大小可以看出，各因子对地价的边际贡献度存在差异。其次，从各变量回归系数的标准差可以看出，各因子对地价的影响存在明显的空间分异。其中，BCP（商服中心繁华度）对地价的影响存在显著的地理变异性。同时，BCP（商服中心繁华度）、SSD（地铁）、GSC（绿地覆盖度）、PD（公园）、FR（规划容积率）变量回归系数最大值、最小值的符号不一致，说明以上因子对地价的边际效应具有方向差异性。

3.2.2 模型对比分析

SLM 模型和MGWR 模型的结果验证了地价同时存在显著的空间自相关和异质性，且地价的空间自相关存在非连续、非平稳的态势。因此，在探讨地价空间格局时有必要考虑空间依赖性和异质性两大特性非平稳并存的特征。在MGWR-SAR 模型估计中，蒙特卡罗检验结果表明所有变量都可以被描述为局域变量，包括空间自相关项。同时，枚举法检验发现，将所有变量视为局域变量的模型的残差平方和，均方根误差，AIC值结果最好。因此，本次选择模型MGWRSAR（1，0，k）进行估计分析（表3），并将MGWR-SAR模型与SLM、MGWR模型的估计效果进行比较（表4）。

表3 MGWR-SAR模型估计结果Tab.3 Estimation results of MGWR-SAR Model

HUANG B 等学者研究认为，如果不同模型之间的AIC值差异超过3 或AIC值相对较小，则表明模型之间存在显著差异[44]。从各模型的拟合优度来看，AIC值从SLM 的221.764、MGWR 的284.051 下降到MGWR-SAR 的128.780，这表明MGWR-SAR 模型在地价空间格局驱动机制的研究中估计效果更好，模型的改进效果显著。

3.2.3 基于MGWR-SAR的地价空间非平稳格局的形成机制

从MGWR-SAR 模型估计结果（表3）来看，各驱动因子的参数不是恒定唯一值，在空间上具有非平稳特征。此外，41.5%的样本的空间自相关回归项系数具有显著性，且系数值存在空间动态变化，表明商服用地地价存在较强的空间依赖性，且空间依赖强度存在非平稳特征。其中，88.5%的显著性样本表现为正相关，集中在鄞州区北部、江北区和镇海区；11.5%的显著性样本表现为负相关，集中在奉化区、海曙区东部（图4）。从地价样本的空间相关性（图5）分布可以看出，样本分布密度高、地价水平高的区域更容易表现出地价空间正相关。正如理论分析所述，当待售地块周围有大量已售地块价格参考时，已售地块地价一定程度上预示或引导着附近待售地块预期价。而在交易数量较少地区，待售地块的价格很难受到相距甚远的其他地区地块的影响，地价的确定更多地是基于对其自身属性价值的判断，因此地价空间自相关性较弱，甚至表现为负相关。

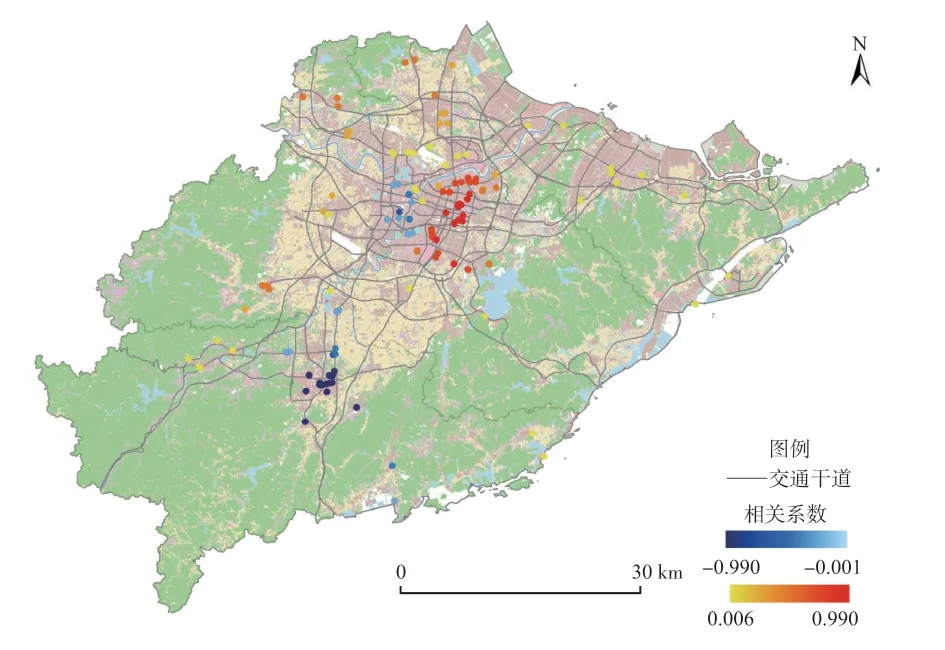
图4 地价空间自相关系数的局部估计值Fig.4 Partial estimates of the spatial autocorrelation coefficient of land price

图5 地价空间自相关系数的显著性Fig.5 Significance of spatial autocorrelation coefficients of land price

以90%显著性水平占比超过样本比例的一半为标准，模型结果显示FON（金融网点）、SSD（地铁）、TD（火车站）、GSC（绿地覆盖度）、BSN（公交站点）对地价存在显著影响（表3）。因此，本文着重分析以上5 个因子对宁波市商服用地地价的空间非平稳性影响。

（1）公共交通便捷度。50.34%的样本显示商服用地周围1 km内BSN（公交站点的数量）对其地价有显著影响，其中，58%显著性样本表现为显著正相关，42%样本则为显著负相关。BSN对商服用地地价的影响呈现明显的空间“两极化”分布，鄞州区西北部样本均表现为显著负向影响，奉化区北部样本则表现为显著正向影响（图6、图7）。这种空间差异主要是由于商服用地的具体用途导致的。奉化区北部样本中约70%地块为住宿餐饮和批发零售用地。对其而言，稳定的客流量和便捷的公共交通是其发展的基本条件，公共交通的便捷度直接影响了公众的消费意愿和可行性，因此该地区BSN对商服用地地价表现出显著的正向作用。鄞州区西北部样本中约79%地块为商务金融用地，这些样本地块处于中心城区且靠近市政府所在地，基础交通设施已发展较为完善，且周边已形成成熟的商圈。不同于住宿餐饮和批发零售业强调大众的可达性，商务金融用地来往的多为固定工作人员，出行目的明确且具有固定周期性，不会因为可达性的略微不足而放弃前往目的地，因此BSN的回归系数多不显著，甚至为负。

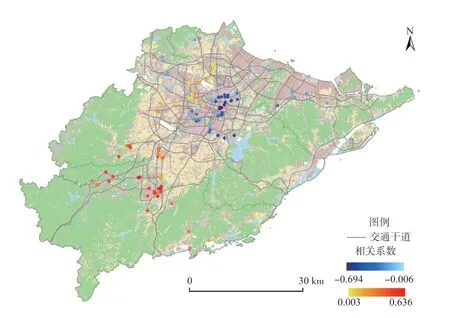
图6 BSN（公交站点数量）系数的局部估计值Fig.6 Partial estimates of the coefficients of BSN (number of bus stops)

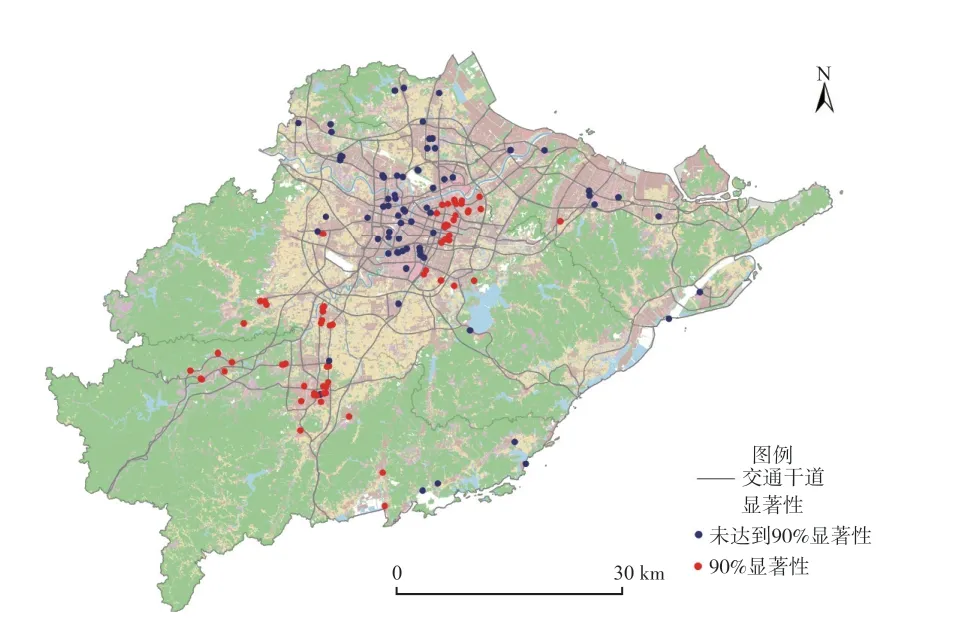
图7 BSN（公交站点数量）系数的显著性Fig.7 Significance of the coefficients of BSN (number of bus stops)

68.03%的样本显示商服用地距离最近地铁站点的距离（SSD）对其地价有显著的负向影响。从影响的空间分布来看，奉化区SSD对商服用地地价的影响高于其他地区（图8、图9）。2016年奉化撤县设区，经济发展水平和基础交通条件落后于其他市辖区，商服吸引力相对较低。作为该区当前唯一的一条地铁干线，3 号线的建设极大地提高居民出行便捷度，地铁站点的人流汇聚能力也为商服活动提供了便利条件[35]。因此，奉化区SSD对商服用地地价的影响显著的高于其他地区。

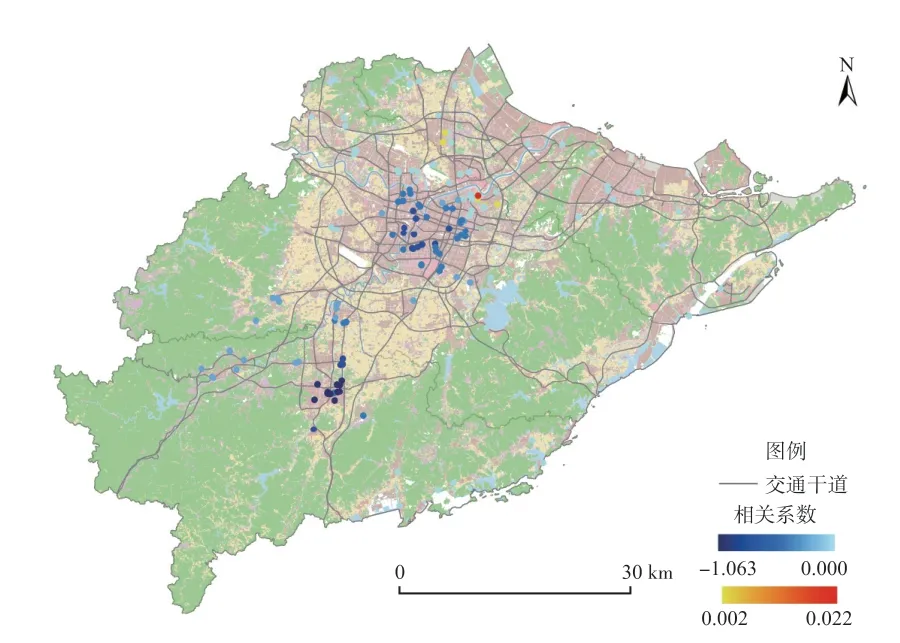
图8 SSD（距地铁站点距离）系数的局部估计值Fig.8 Partial estimates of the coefficients of SSD (distance from subway station)

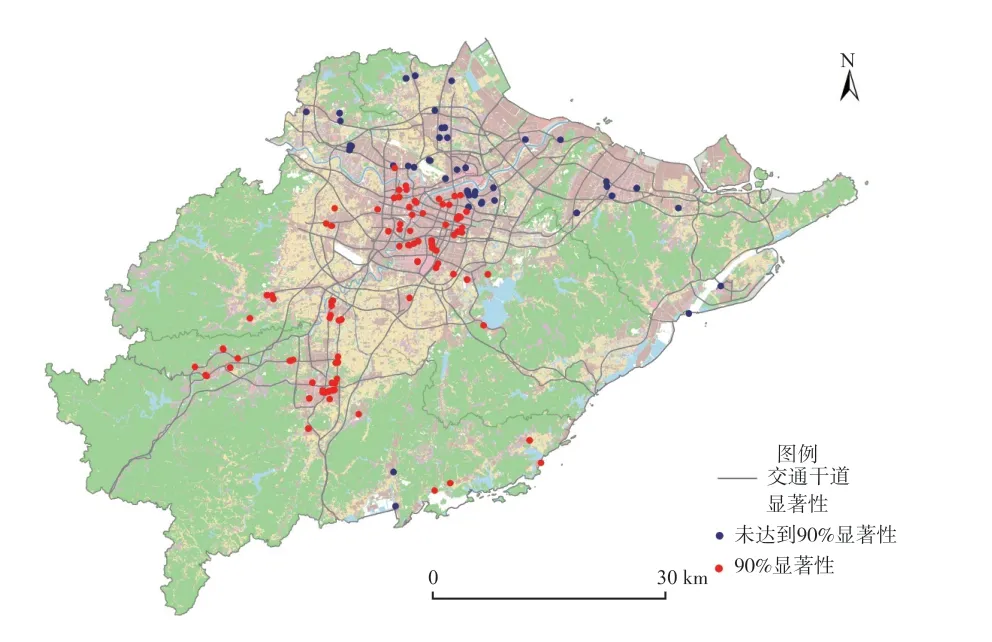
图9 SSD（距地铁站点距离）系数的显著性Fig9 Significance of the SSD (distance from subway station) coefficients

（2）对外交通便捷度。63.95%的样本显示商服用地距火车站的距离（TD）对其地价有显著影响，并且80%的显著性样本表现为显著负相关（图10、图11）。显著性样本的具体用途多为商务金融用地，对外交通便捷度的提高会加强地域间商务往来的便利度，提升商服营收潜力，进而导致用地价格的上涨。

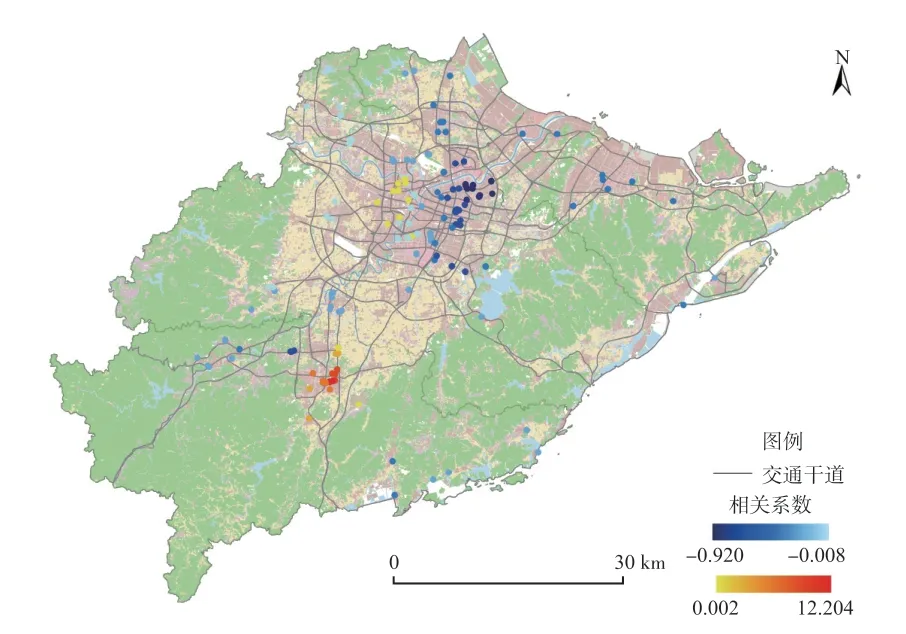
图10 TD（距火车站距离）系数的局部估计值Fig.10 Partial estimate of the TD (distance to train station) coefficients

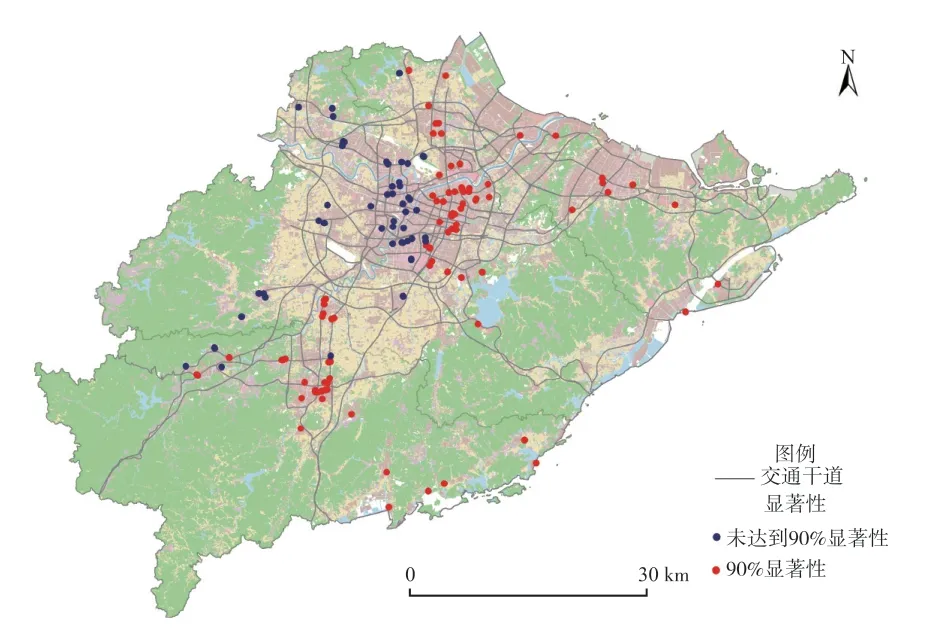
图11 TD（距火车站距离）系数的显著性Fig.11 Significance of TD (distance from train station)coefficients

（3）基础设施状况。71.43%的样本显示商服用地周围1 km内金融网点的数量（FON）对其地价有显著影响，其中87.62%表现为显著正相关（图12、图13）。这表明金融网点的数量对商服地价存在显著正向效应。

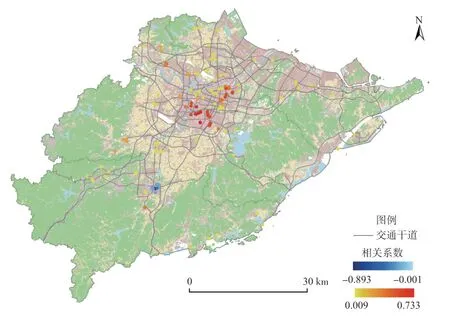
图12 FON（金融网点数量）系数的局部估计值Fig.12 Partial estimates of the coefficients of FON(number of financial outlets)

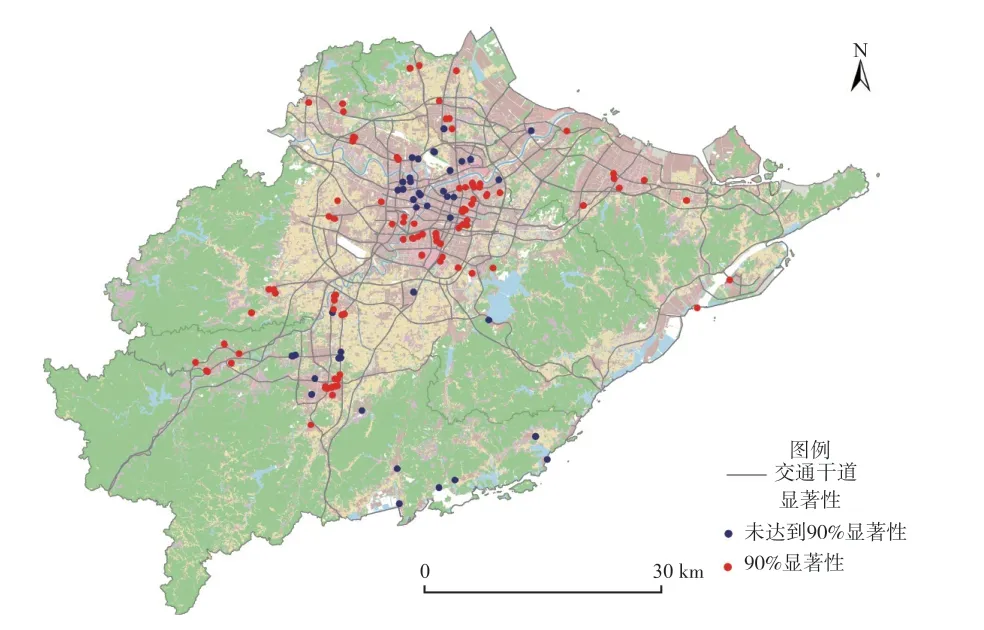
图13 FON（金融网点数量）系数的显著性Fig.13 Significance of the coefficients of FON (number of financial outlets)

（4）环境条件状况。57.14%的样本显示绿地覆盖度（GSC）对商服用地地价有显著影响，其中55.95%样本表现为正相关，其余为负相关。影响效应在空间上表现出显著的差异格局，鄞州区北部、江北区东南部样本多为显著正相关，海曙区东部、鄞州区西部样本多呈现负相关（图14、图15）。鄞州北部作为宁波市政府和宁波东部新城金融商务区的所在地，商服用地类型以商务金融和高端服务业为主，公园绿地数量相对较少。在公园绿地生态系统服务水平较低的状况下，公园绿地的增加会给周边土地带来增值效应。而鄞州区西部和海曙区东部住宅较为集中，公园数量分布较为密集。当公园绿地供应超过一定水平后，其增值效应将大幅降低并维持在一个相对稳定的水平上[45]，因此公园绿地对于其土地的增值效应就没有那么的明显。

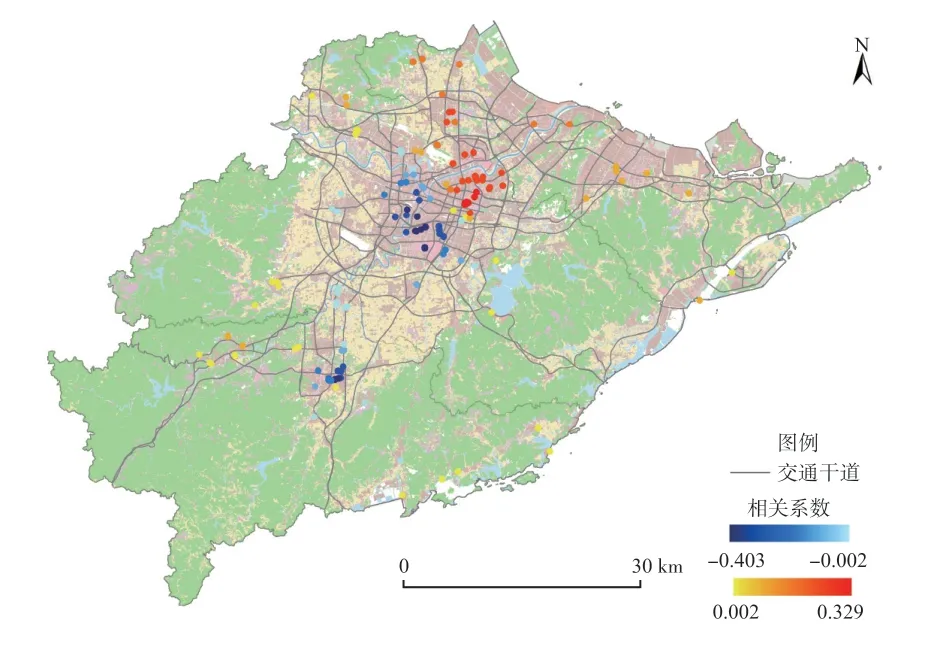
图14 GSC（绿地覆盖度）系数的局部估计值Fig.14 Partial estimates of the GSC (green space coverage) coefficients

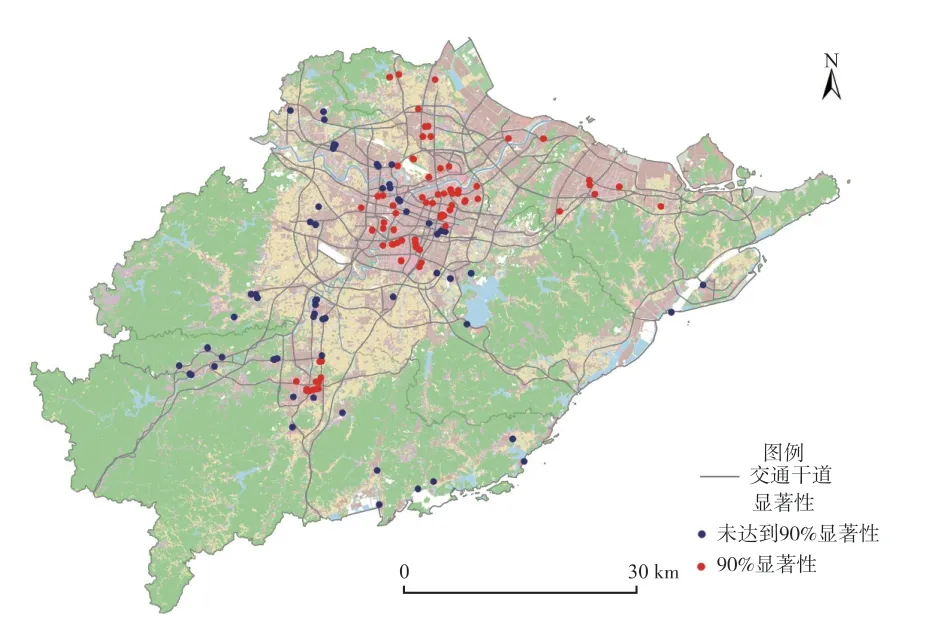
图15 GSC（绿地覆盖度）系数的显著性Fig.15 Significance of the GSC (green space coverage) coefficients

由此可见，不同于SLM模型λ项系数仅能反映地价平均空间依赖强度，MGWR-SAR模型结果中的WY项系数可以反映地价空间依赖强度的动态变化（图4、图5）。MGWR 模型与MGWR-SAR 模型运算结果中（表2、表3），部分地价驱动因子空间作用趋势存在明显差异。这是由于两个模型关注的空间特性维度不同造成的，相较于SLM 模型和MGWR 模型仅关注地价的单一空间特性维度，MGWR-SAR 模型兼顾测度地价两类空间属性。但从上述主要驱动因素的空间异质性分析来看，MGWR-SAR模型较MGWR模型在地价空间异质性格局的测度识别上更符合地价实际空间发展趋势。相较于SLM 模型和MGWR 模型，MGWR-SAR模型在模型拟合性和解释力上均有明显的优势。

4 结论

地价作为城市空间利用变化的重要驱动力，直接影响着城市形态和经济结构的调整与发展。因此，识别城市地价的空间格局及其形成机制，对城市经济及其空间管理具有重要的理论和实践意义。但当前国内有关地价空间非平稳格局研究中，常用的空间模型无法测度地价空间依赖强度的动态变化，未兼顾处理地价空间依赖性和空间异质性具有非平稳特征，模型估计的偏差降低了对地价空间格局识别的准确度，影响城市土地资源空间配置优化。因此，空间测度技术的改良是当前地价空间研究中不可忽视的问题。

本文在明晰城市地价空间非平稳格局形成机制的基础上，探索将空间计量经济学前沿技术——GENIAUX等[14]提出的MGWR-SAR模型首次应用于国内地价研究，改进当前常用的地价估计方法及模型，重新考察我国地价的空间形态。以浙江省宁波市城六区商服用地地价数据为案例，实证检验MGWRSAR 模型相较于传统空间计量模型的建模效果。研究表明：（1）绝对区位的固定性引导地理邻近地区间地价存在空间依赖性，且土地市场活跃地区地价空间依赖性更强。而相对区位的不均衡致使地价呈现空间异质性。地价空间依赖性的非线性与空间异质性综合作用形成非平稳的地价空间格局。（2）地价具有空间依赖性和空间异质性两大特性非平稳并存的特征，这一特征要求测度模型同时将空间自相关参数项和空间异质性参数项嵌入空间变化系数，考虑空间参数异构情况。（3）实证结果表明，相较于常用的空间计量模型，MGWR-SAR 模型在地价空间非平稳格局测度及决定因素研究中的估计效果更佳。新测度技术的应用需要实践的反复检验，后续研究中会继续扩大模型的检验范围，在测度对比多尺度多类型的地价空间研究结果的基础上加以推广应用，为其他地理要素空间测度研究提供技术参考。