“控制工程基础”互动案例式教学改革与实践

王 昱，王艳辉，梁 宵

（沈阳航空航天大学 自动化学院，辽宁 沈阳 110136）

2017年2月以来，教育部积极推进新工科建设，号召培养在工程领域有工科基本的理论知识、过硬的专业技能，在实际的生产中能够依据工科思维做出可行性分析决策的高级新型复合工程师［1］，这对于全国各工科院校的教育教学模式提出了新的挑战。

一、“控制工程基础”课程概述

“控制工程基础”是沈阳航空航天大学面向机械、车辆、航宇、能环等非控制类专业的一门重要专业基础课，主要研究经典控制论中的单输入—单输出控制系统的分析和校正方法。无论从名称还是内容上看，课程都是控制理论与工程应用的有机结合体。因此，如何充分利用时长有限的课堂教学，达成既能够使学生深入理解控制理论的精髓，又能实现与工程应用有效融合的目标，成为近年来课题组教学改革的重要课题。

二、课程教学中存在的问题

目前课程存在如下两方面矛盾影响授课效果。

（一）课程对理论理解能力的高要求与学生基础知识薄弱的矛盾

“控制工程基础”课程知识点众多，涉及高等数学、理论力学、电工电子等学科，如果学生前置课程的知识储备不足，就会导致理论理解困难，转而将注意力放到计算步骤和结果上，把控制学成了数学。

（二）教师“一言堂”的授课模式与学生工程实践能力培养需求的矛盾

传统的课程教学模式以教师为主体进行理论讲授，强调计算方法，缺少实例引导，导致学生学习目的不明确，只知其然而不知其所以然，大大减弱了学生对课程的学习兴趣及课堂参与度，导致学生不仅不能很好地掌握所学内容，更难以将理论应用于实际。

三、互动案例式教学的改革举措

鉴于上述问题，课题组以重塑学生在学习中的主导地位，激发学生学习的主观能动性，加强学生对重要理论的理解，提升学生解决实际问题的工程实践能力为宗旨，经过不断学习、积极探索，成功将案例教学法［2］引入课堂，逐步形成了具有自己风格的互动案例式教学模式。具体措施如下。

结合学生的日常生活及专业背景，针对重要理论精编局部小型案例及贯穿型项目案例构建案例库，如以天宫机械臂等案例说明控制的概念；以抽水马桶等案例描述反馈的作用；分机械类（如人造卫星姿态运动系统）、电气类（如扬声器）、过程控制类（如水箱）案例解读数学模型的建立方法；以倒立摆、外科手术的激光操作控制系统［3］等案例进行多重知识点的阐释。

针对每个教学案例设置启发引导性问题，进行模块化教学设计。同时，为了强调学习过程的重要性并突出学生的主体地位，提出并采用了“案例导入—理论推导—知识总结—仿真验证—引发思考—思想政治教育”的进阶式“六步教学法”。

有效应用MATLAB［4］等现代化辅助教学工具，针对教学案例精心设计仿真实验，通过结果对比在理论教学中增加对所选案例系统的性能分析和控制效果的直观显示，使学生加深对理论知识的理解，提升对课程的兴趣，间接提高动手能力。

四、互动案例式教学实施举例

课程教材中明确指出了开环和闭环两种控制方式的定义和特点［5］。为了使学生更好地理解相关内容，这里选用贯穿型案例——车速控制系统［6］，采用“六步教学法”进行互动案例式教学设计。

（一）案例导入

首先进行案例描述。安装了气动发动机的汽车行驶在公路上，其车速控制过程如下：控制器根据期望车速r输出控制量——调节气门的角度u，控制实际车速y，过程的主要干扰为路面坡度的变化w。根据上述描述绘制系统的开环控制框图，如图1所示，同时设置提问：该系统控制器如何设计？

图1 车速开环控制系统框图

（二）理论推导

设置一组简单的变量线性关系构建系统静态数学模型：当车速为65 mile/h时，调速气门每改变1度，可引起10 mile/h的速度变化；坡度每改变1%，引起5 mile/h速度的改变。

引导学生分析开环控制器的设计方案：实际控制时并不能预知干扰的种类和大小，且开环系统在干扰对输出产生影响时不具备通知输入端调整控制量的能力，因此设计控制器时只能凭借经验考虑从输入到输出的支路在理想情况下进行车速控制，因此欲实现y=r的目标，控制器的表达式应为0.1。

依据上述假定对图1模型进行数学计算：由u=0.1r，yol=10（u-0.5w），推导出开环系统的误差为eol=r-yol=5w。引导学生分析：开环控制的误差只跟干扰有关，与其大小成正比。

进一步启发学生思考：开环系统由于缺少输出与输入之间的反向连接，导致干扰对输出产生影响时控制量不能做出调整，影响控制精度。因此，为了提高控制准确性，需要在开环系统的基础上增加对输出的检测（反馈），使输出参与到控制中，实现闭环控制。并由此通过改变图1绘制车速闭环控制系统框图，如图2所示。

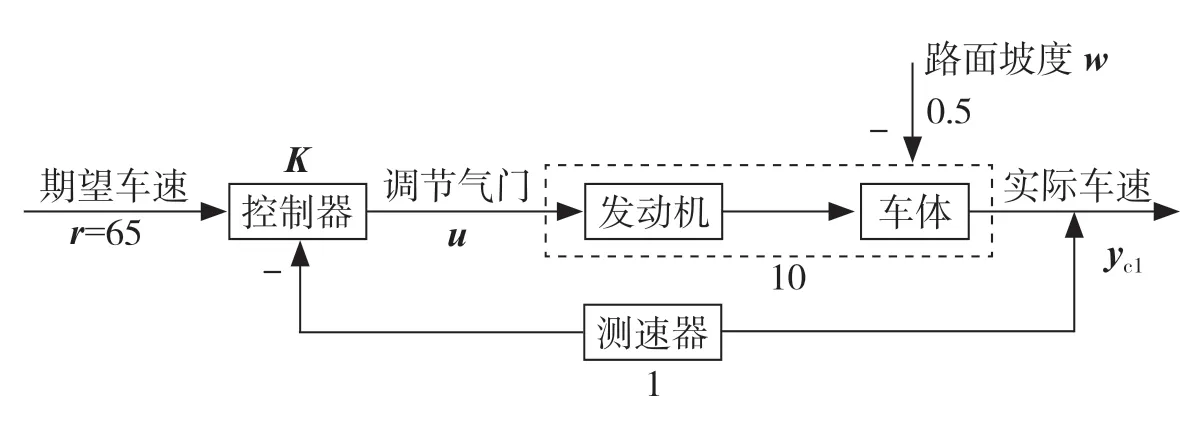
图2 车速闭环控制系统框图

在前面线性关系的基础上做进一步假设：设测速器可以实现1∶1的转速检测，同时为简单起见，将可调控制器设为比例控制K，将上述关系输入框图2，得到车速闭环控制系统的数学模型。

与学生对闭环系统进行数学推导，计算并分析控制精度：由ycl=10（u-0.5w），u=K（r-ycl），推导出闭环控制误差为。

引导学生分析：闭环系统的误差不仅和干扰有关还和输入有关，因此即使干扰为0，系统也会存在误差；当干扰出现时，闭环控制可以通过改变控制器增益K减小误差，K越大，误差越小，控制效果明显优于开环控制；另外，与开环相似，当输入一定时，闭环控制的误差随干扰的增大而增大。

（三）知识总结

对上述推导结果进行总结：开环控制由于缺少反馈，输出量并不会返回到输入端参与控制，控制器传输关系完全依据期望输入凭借经验给出并在整个过程中保持不变，因此输出平稳；但由于确定控制量的过程中并没有考虑干扰，因此在干扰较大时，系统的准确性会变差。而闭环控制则由于引入反馈将干扰对输出的不利影响通过偏差体现，即输出参与控制，再通过改变控制量校正偏差，控制精度更高，验证了教材中理论知识的正确性。

（四）仿真验证

对上述理论内容和数学推导应用MATLAB进行仿真。为区分明显，仿真中假定输入r和w干扰分别于0时刻和1时刻起作用，仿真分两步进行：首先进行开环控制仿真，将w分别取0、1、5，进行不同干扰下的输出曲线比较，结果如图3所示。可以看出在三种干扰作用下的最终车速分别为65、60和40，误差逐渐增大且与干扰大小成正比（eol=5w），与前面理论推导的结论一致。

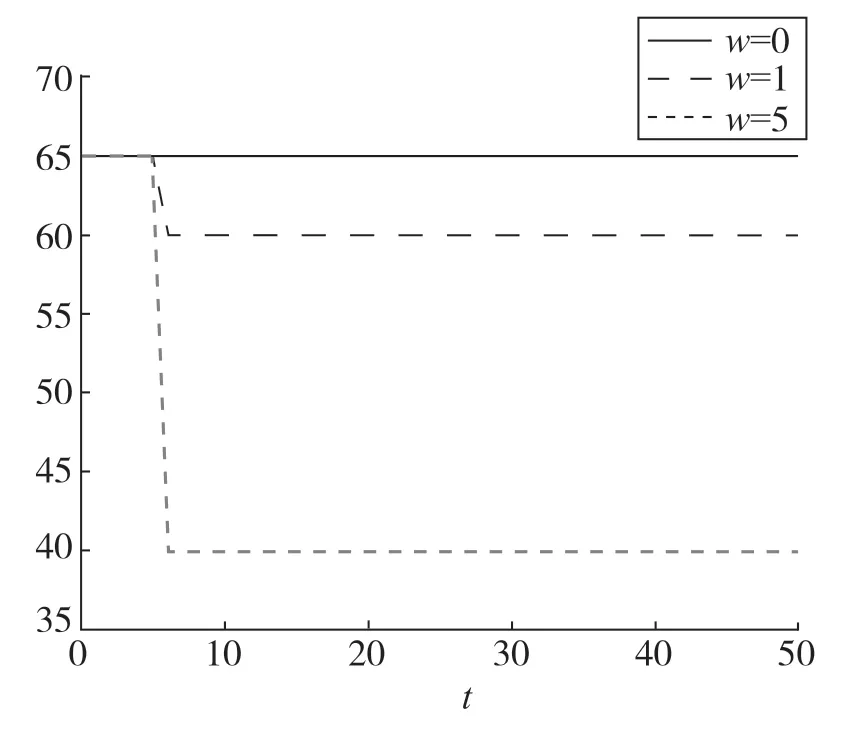
图3 开环系统控制仿真

再进行不同控制器增益下的闭环控制仿真：分别将K设为10和100，同进行w=0，1，5三种干扰下的控制仿真，结果如图4所示。对比两组曲线可以看出，闭环控制下即使在w=0时，输出也不能够完全达到输入，控制精度不如开环；而当存在干扰时，虽然与开环相似，输出误差随着w的增大而增大。但对于相同的干扰，闭环系统输出的精度明显更高，同时可以看出增益K越大，误差越小精度越高，与上述理论分析的结论亦一致。

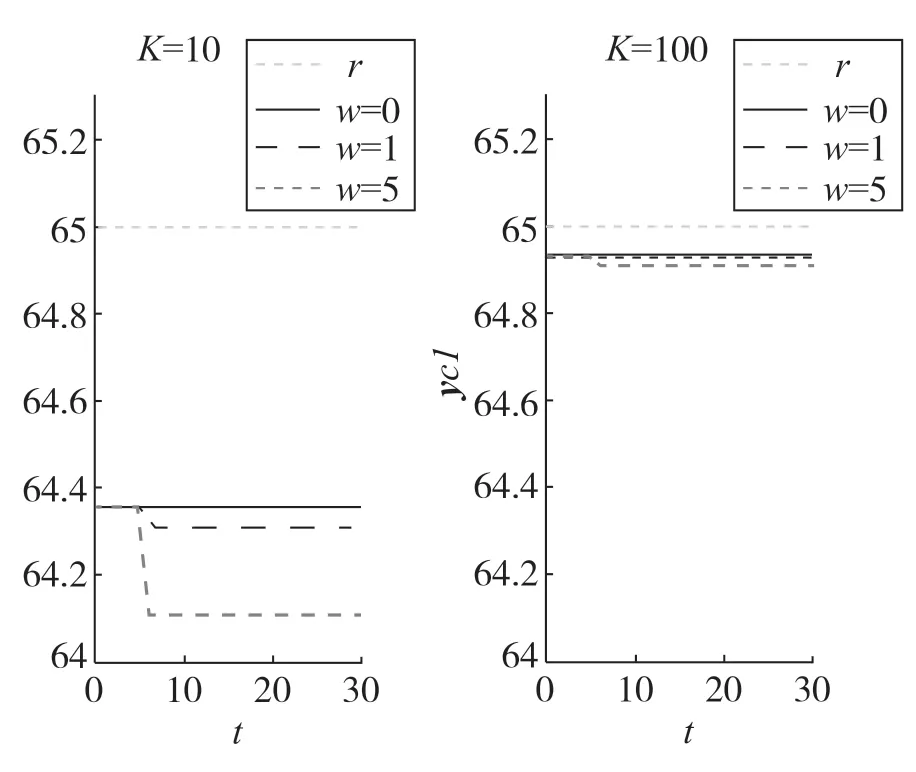
图4 闭环系统控制仿真

（五）引发思考

设置两个进阶提问，引发学生进一步思考。

思考1：如前所述，K越大，闭环系统的准确性越好，但是不是K越大系统性能一定越好呢？

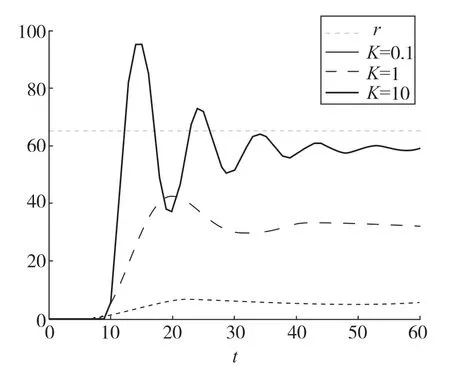
图5 改变对象数学模型的闭环控制仿真

引导学生分析：改变被控对象后，虽然随着K值的增大，系统的误差明显减小，但系统的稳定性却逐渐变差，同时达到稳态的快速性也变差。由此引出后续课程的内容——控制系统的三大性能要求：稳定性、准确性、快速性，强调稳定性是系统得以工作的首要条件。

（六）思想政治教育

在案例教学的最后引入思想政治教育，帮助学生树立正确的人生观。本案例中由控制系统性能指标之间的矛盾性引导学生联想到工作和学习中遇到难以面面俱到的问题时，要学会抓主要矛盾，增强“识大体，顾大局，寻求合作共赢”的优化意识。

结语

综上所述，将互动案例式教学法引入控制工程基础课堂教学，采用现代化教学手段通过案例导入、理论推导、知识总结、实验验证、引发思考和思想政治教育等环节能够全方位调动学生对知识学习的主观能动性，使学生在教师的引导下，通过积极探索寻求控制规律，愉快地进行理论学习，不仅能够深入理解课程内容，而且可以通过思想政治教育促进学生的全面发展。教学实践表明，恰当的生活和工程化案例以及具有亲和力的互动式教学方式能够在引起学生共鸣的同时，使学生从完全陌生到对晦涩的控制理论产生兴趣，于无形中建立起理论与实践的有效连接，增强新工科背景下的创新意识以及分析和解决工程实际问题的能力，取得了良好的教学效果，值得推广。