基于Richards 方程的冷杉树高曲线深度神经网络激活函数*

徐奇刚 雷相东 郑 宇 胡兴国 雷渊才 何 潇

（1. 中国林业科学研究院资源信息研究所 北京 100091；2. 国家林业和草原局华东调查规划院 杭州 310000；3. 国家林业和草原局森林经营与生长模拟实验室 北京 100091；4. 吉林省汪清林业局 汪清 133200）

随着计算机计算能力的大幅提升以及机器学习算法的突飞猛进，森林生长建模面临新的机遇和挑战，既要满足处理大数据建模的需求，同时对估计精度的要求也越来越高。从“最佳有用”原则出发，机器学习算法，尤其是深度神经网络算法具有对数据分布不作要求、可处理非线性数据、能处理连续和分类变量、预测精度高、数据适应力强等优势，在林业建模领域的具有广泛的应用前景（Humphrieset al.，2018；雷相东，2019），常用机器学习算法，如多元自适应回归样条、神经网络、随机森林、支持向量机和增强回归树等已应用于树高-胸径关系（梁瑞婷等，2021；李际平等，1996；陈佳琦等，2020）、单木直径生长（Ouet al.，2019；Vieiraet al.，2018；马翔宇等，2009；Reiset al.，2016；浦瑞良等，1999）和枯死模型（Mezeiet al.，2014；Sproullet al.，2015；Oguroet al.，2015；Hasenaueret al.，2001）等森林生长收获预估领域。

然而，机器学习算法在林业建模应用过程中存在一个潜在缺点，即一个回归模型的输出可能不符合生物学逻辑。例如，在一个不被限制输出的树高生长神经网络模型中，若未设置树高的最大渐进值，随着年龄增长，模型可能会输出一个不断变大偏离常识的树高值；在林分直径生长模型中，一个数据清洗不够彻底、训练不够细致的神经网络模型可能输出负值。这些问题导致科研工作者在构建类似模型时仍更倾向于采用符合生物学逻辑的传统回归方法，如理论生长方程。

神经网络模型在林业上的应用历史较长（Hasenaueret al.，2001；Vinícius Oliveira Castroet al.，2013；Tavares Júnioret al.，2019），其处理过程主要通过激活函数实现，激活函数赋予神经网络非线性的特性，将输入转换成输出（雷相东，2019）。该过程中，最终输出为最后一层神经元经激活函数转换得到，故可在输出层嵌套提前设计好的激活函数，以控制模型输出使其符合预期，如对多标签分类问题采用Softmax 函数方式（Liuet al.，2016）。但迄今为止，如何通过激活函数解决模型输出违背生物学规律的问题仍未得到解决。

鉴于此，本研究提出一个基于理论生长方程（Richards 公式）的激活函数，解决神经网络算法在森林生长建模时输出可能不符合生物学规律的问题，并以臭冷杉（Abies nephrolepis）解析木树高-胸径数据为例进行验证。新提出的激活函数可视作传统方法与机器学习算法的结合，为神经网络在森林生长建模方面的应用提供一个新的思路和方法。

1 研究区概况

研究区位于吉林省汪清林业局金沟岭林场，地理位置为129°56′—131°04′E，43°05′—43°40′N。林场森林总面积16 286 hm2，海拔30～1 200 m，全年平均气温3.9 ℃左右，属低山丘陵地貌。森林类型是以红松（Pinus koraiensis）、云冷杉为优势树种的天然针阔叶混交林，主要树种包括鱼鳞云杉（Picea jezoensis）、红松、枫桦（Betula costata）、臭冷杉、水曲柳（Fraxinus mandschurica）、黄菠萝（Phellodendron amurense）、白桦（Betula platyphylla）、胡桃楸（Juglans mandshurica）等。

2 数据与方法

2.1 数据

数据源自1988 年8 月吉林省汪清林业局金沟岭林场臭冷杉解析木数据，树干解析流程见孟宪宇（2006）。在0 m（0 号盘）、1.3 m（1 号盘）、3.6 m（2 号盘）、5.6 m（3 号盘）等树高处截取圆盘，查数各圆盘的年轮数。各龄阶树高采用内插法按比例得到，各龄阶去皮胸径通过1.3 m 圆盘（1 号盘）测量得到，应用树皮系数（本研究臭冷杉树皮系数为1.072）转换得到带皮胸径。共计96 株伐倒木、458 组树高-胸径观测数据，以8∶2 划分建模集和测试集，366 组数据用于建模，92 组数据用于检验，单木树高-胸径统计量见表1。

表1 单木树高-胸径统计量Tab. 1 Statistics of tree height and diameter at breast height

2.2 深度神经网络模型和新的基于理论生长方程的激活函数

深度神经网络模型是一个拥有复杂层数和神经元结构的多层感知机模型，由输入层、多层隐藏层和输出层组成，层与层的单元全连接，将上一层输出作为下一层输入，通过激活函数转化后继续作为下一层输出，逐层向后直至运算到输出层，用梯度下降来最小化函数近似误差（Goodfellowet al.，2016）。由于其强大的函数逼近能力，对输入变量无统计上的分布要求，预测精度高，是现阶段应用最广的人工神经网络。

对于一个L层的多层神经网络（Rumelhartet al.，1986；Sibiet al.，2013），令输入向量为：

输出向量为：

第l隐藏层神经元的输出为：

则最后一层神经元的输出为：

式中：sl为第l层神经元个数；sL-1为第L-1层神经元个数；为第L-1层神经元到第L层神经元的权重为第L层第k个神经元的偏置（bias）；第L层第k个神经元激活函数内部值。

样本总误差为：

式中：N为输入数据集的观测样本量；dk(q)为第q个训练样本的观测值；yk(q)为第q个训练样本神经网络输出值。

反向传播（BP）算法每次迭代按以下方式对权值和偏置进行更新：

在处理回归问题时，现阶段比较流行的做法是取输出层（第L层）为线性激活函数，即：

此时，对于单个训练样本，BP 算法下输出层参数的梯度更新公式为：

式中：t为第t轮训练轮次；E(q)为第q个训练样本的损失函数值。

如此处理对输出层没有任何限制，但用于森林生长建模时存在缺陷，故本研究对最后一层即输出层的激活函数进行调整（图1），引入最常用的理论生长方程Richards 式，作为修正后最后输出层的激活函数：

图1 神经网络模型的激活函数修正Fig. 1 Modified activation function of neural networks

式中：a、b和c为Richards 方程的3 个参数。

在反向传播算法中，神经网络模型Richards 激活函数的导数为：

此时，输出层参数的梯度更新公式变为：

本研究中，Richards 方程的3 个参数a、b和c于R 语言平台使用nls()函数（Ihakaet al.，1996）进行传统非线性回归拟合得到，采用默认的高斯-牛顿迭代算法。最终，a取20.689、b取0.070、c取1.418，即新的激活函数为：

2.3 模型比较与结构设计

除传统回归方法外，本研究比较3 种不同激活函数设置的深度神经网络模型（表2）。

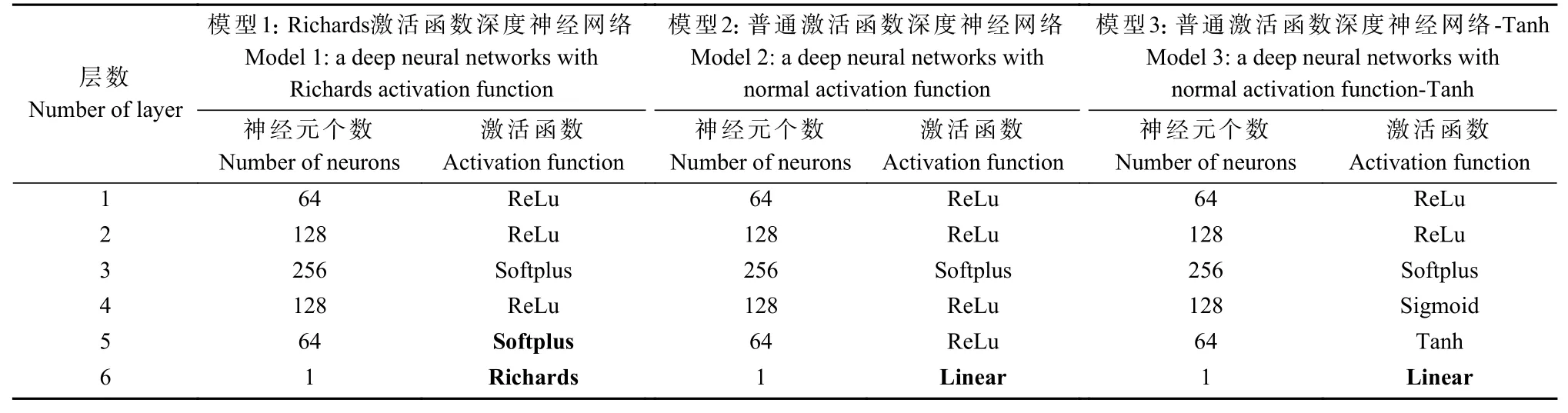
表2 3 个深度神经网络模型结构与激活函数Tab. 2 Structure and activation functions of three deep neural network models

模型1 为使用Richards 公式作为输出层（第L层）激活函数的深度神经网络模型。梯度优化算法选择“Adam”（Kingmaet al.，2014）。隐藏层激活函数选择上，由于Sigmoid 函数具有广泛的饱和性使梯度下降变得困难，整流线性函数ReLU 的行为更接近线性，模型更容易优化，通常情况下表现良好（Goodfellowet al.，2016），故本研究在大多数情况下选用整流线性函数；又考虑到ReLU 函数可能存在Dead ReLU 问题，即对小于0 的输入的正向输出和反向梯度更新值均为0，神经元“死亡”，故在第3 层选用Sotfplus 函数。输出层激活函数使用Richards 公式（式15）。Richards公式本身在x大于0 时才能满足输出一定大于0，为使神经网络模型输出一定大于1.3，对第L-1 层神经元进行限制，激活函数选择输出一定大于0 的Softplus函数，并且通过指定第L层参数use_bias 为False，删去最后一层的偏置指定kernel_constraint 为NonNeg()，限定非负，使最终模型1 的输出能一定大于1.3。

对于隐藏层与隐单元数量的最优网络设计问题，采用反复试错法‘try and error’（Uzunet al.，2017），观测模型在测试集上的误差得到。batch_size 设为64，Epoch 设为1 000 轮。Callbacks 采用ModelCheckpoint策略，save_best_only 设为True，即只保存1 000 轮中损失值最小的模型。

模型2 为使用式（8）作为输出层（第L层）激活函数的深度神经网络模型。除第L-1 层使用ReLU 激活函数外，其余结构设计与各项训练参数与模型1 一致。

模型3 为使用式（8）作为输出层（第L层）激活函数的深度神经网络模型。由于模型2 的激活函数行为接近线性，故加入模型3 作为对比，其结构设计与各项训练参数与模型2 一致。与模型2 不同的是，模型3 最后一层隐藏层（第5 层）的激活函数选择Tanh函数，第4 层选择Sigmoid 函数，以此观察隐藏层中带有常见非线性激活函数的深度神经网络模型表现。

深度神经网络模型的建立和实现采用Python 语言的keras（Gulliet al.，2017）和tansorflow（Abadiet al.，2016）模块完成。

2.4 模型评价

选取决定系数（R2）、均方根误差（root mean squared error，RMSE）和平均绝对误差（mean absolute error，MAE）作为模型评价指标：

式中：n为样本数；Hi为第i株单木的树高观测值；为第i株单木的树高预测值；为样本内单木树高观测值的平均值。

3 结果与分析

3.1 基于Richards 激活函数的深度神经网络模型

4 种模型训练集和测试集精度检验结果如表3 所示。传统模型、使用Richards 激活函数的模型1、与隐藏层使用Tanh 和Sigmoid 函数的模型3 精度表现非常接近。模型1 表现最好，从训练集来看，R2比传统模型提升0.051%，RMSE 和MAE 比传统模型分别下降0.322%和0.117%；从测试集来看，R2比传统模型提升0.175%，RMSE 和MAE 比传统模型分别下降2.282%和4.011%。模型2 训练集R2比传统模型降低0.140%，RMSE 和MAE 比传统模型分别提高0.876%和0.036%；测试集R2比传统模型降低0.598%，RMSE和MAE 比传统模型分别提高4.591%和2.378%。模型3 训练集R2比传统模型训练集提升0.422%，RMSE和MAE 比传统模型分别降低2.681%和2.242%；测试集R2比传统模型降低0.476%，RMSE 和MAE 比传统模型分别提高3.529%和0.185%。

表3 4 种模型精度检验结果Tab. 3 Accuracy test statistics based on 4 models

3.2 模拟环境下4 种模型的输出表现

对于已建立好的臭冷杉树高-胸径传统模型和3种深度神经网络模型，本研究模拟0～100 cm 胸径区间观察4 种模型的输出表现。输入数据为服从[0,100)均匀分布的1 000 组胸径数据，输出树高如图2 所示。使用Richards 激活函数的深度神经网络模拟图与使用传统方法表现类似，均有明显的树高最大渐进值20.69 m。模型2 输出树高随胸径增长呈线性递增关系，但没有树高最大渐进值，不符合生物学逻辑。模型3 虽然表现出树高在20.0 m 达到最大值，但曲线不光滑，模拟的胸径超出训练数据胸径最大值（29.38 cm）后模型预测树高达到最大值后保持恒定。

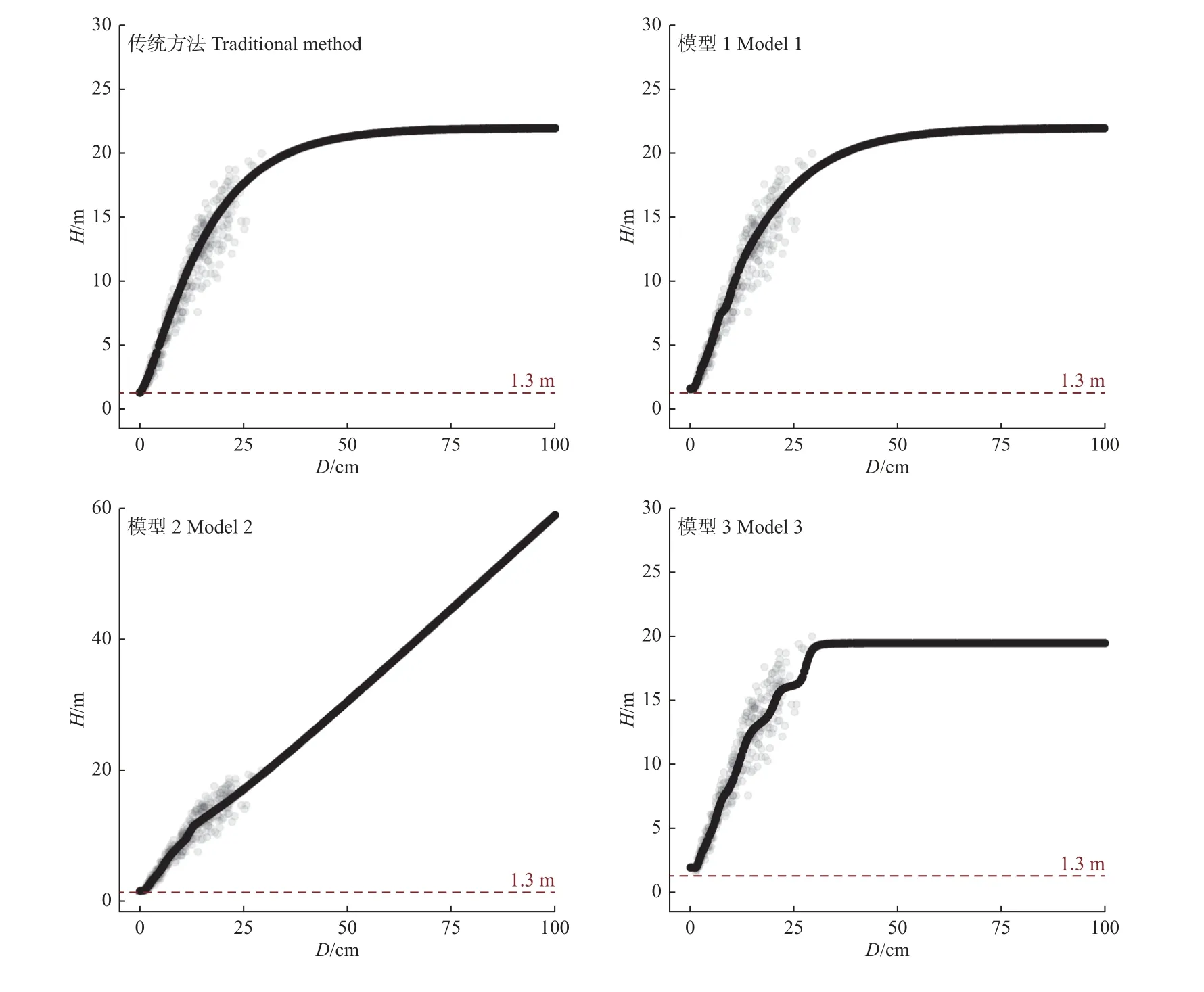
图2 4 种模型在胸径0～100 cm 情况下的输出树高Fig. 2 Predicted tree heights from 4 models with simulated diameter from 0 to 100 cm

4 讨论

本研究提出一个基于Richards 方程的树高-胸径深度神经网络激活函数，从模型检验结果来看，使用Richards 激活函数的深度神经网络模型相比传统非线性回归模型（直接使用Richards 公式拟合）精度略有提高，测试集R2提升0.175%，RMSE 和MAE 分别降低2.282%和4.011%，总体上看神经网络模型与传统非线性回归模型结果接近，与以往研究结果类似（徐奇刚等，2019；Özçelıket al.，2010；2017；Vahedi，2016）。Shen 等（2020）采用人工神经网络方法建立广东省杨树（Populus）人工林树高-胸径模型，与传统非线性回归方法进行比较，结果显示神经网络树高-胸径模型的R2增加10.3%，RMSE 和MAE 分别减少12%和13.5%，神经网络方法拥有更高的泛化潜力。本研究中模型1 与传统方法构建的Richards 模型最关键的区别在于其在胸径与树高的映射中间增加了一层映射关系，即最后一层神经元值与胸径之间的映射，通过基于Richards 公式的激活函数估计树高，这样处理可使模型表达出更精细的信息。使用Richards 激活函数的模型1 相比使用传统激活函数的模型3 精度也有所提升，测试集R2提升0.653%，RMSE 和MAE 分别降低5.613%与4.189%，这可能是因为Richards 的a、b和c参数值与Richards 本身的模型形式作为先验信息加入神经网络训练过程，提高了模型精度。

在传统非线性回归建模过程中，Richards 等理论生长方程的各参数均具有生物学意义，且在树高-胸径模型中表现优异（Xuet al.，2022）。Lei 等（1997）论证树高-胸径关系时指出，在树高-胸径基础模型选择期间，应同时考虑数据相关及合理的生物学标准。一个合理的模型形式应该具有单调增量（dH/dD＞0）、S拐点（存在二阶导为0）和最大渐进值。对于树高-胸径模型，Richards 公式中a代表树高生长的最大渐进值，b代表相对生长速率参数。各树种的参数值相对接近，林业工作者能够依据工作建模经验选择合适的参数初值，使模型更加容易收敛，同时也能使模型输出保证在符合生物学逻辑的合理范围内。而基于机器学习算法的模型在建模数据处理不够细致、超参数调整粗糙的情况下，可能会出现树高无限增大甚至出现负值的现象。本研究模拟结果显示，使用传统神经网络激活函数的模型2 和模型3 的输出存在树高没有最大值以及模型在训练集数据区间外预测值失真的情况，由于树高生长存在极限，且树高与胸径并不是线性关系。而使用Richards 激活函数的模拟结果与传统方法建立模型的模拟结果类似，避免树高随胸径的线性增长，更符合生物学规律。

需要指出的是，在传统回归中，模型渐进值的确定取决于数据和基础模型本身，如对于同一组观测，舒马赫模型预测的渐进值往往会比其他模型更大（Lee，2000），又如若用于拟合的数据本身树高偏低，得到的树高最大渐进值较低会导致出现与实际树高最大值不相符合的情况（区域内的树高最大值出现在样地之外）。本研究中，Richards 公式作为激活函数加入神经网络输出层，公式中代表树高最大渐进值的参数a和代表相对生长速率的参数b是来自预先拟合好的非线性回归模型的参数结果，若数据本身覆盖范围不够大，模型的泛化性能可能受到影响。预先设置好的参数值在模型训练后不会被改变，神经网络通过梯度更新，将输入层变量与输出层变量的函数关系均映射在网络本身的权值中，并不会影响输出层激活函数。与此同时，a、b和c参数也因为反向传播算法影响每次更新的梯度变化值，对模型训练产生直接影响；如果a、b和c参数设置不合理，会对模型训练产生负面效果。

神经网络模型是数据驱动模型，在输出层加入Richards 激活函数并不能保证模型输出一定存在渐近线，因为当训练数据存在“倒长”，即数据中胸径较大时对应的树高小于胸径较小时对应的树高，那么神经网络模型会被影响，以致最后一层的神经元值与胸径在该区间内呈负相关，模型则会失去渐近线，同时也会造成模型在该区间预测时曲线并非单调递增，但Richards 函数本身形式保证模型输出一定存在一个合理的最大值。同理，由于神经网络的权值更新由建模数据驱动，虽然基于Richards 公式激活函数的神经网络模型不能保证在胸径为0 时树高一定等于1.3，但对第L-1 层的神经元进行合理限制后可保证模型输出一定大于1.3。在神经网络模型中，若试图使dH/dD一定大于0，则需要施加限制使网络中的权值W、偏置b以及组成网络各激活函数的导数一定大于0，这种情况下，BP 算法拟合模型极其容易梯度消失，难以收敛，因此本研究并未加入这方面的限制。

本研究也比较了林业中其他常用的理论生长方程，如逻辑斯蒂和考尔夫公式，拟合效果均不如Richards 公式，故选择Richards 公式作为输出层的激活函数参考形式。虽然本研究最终确定的激活函数为Richards 方程，但从原理上讲，基于理论生长方程修正神经网络激活函数从而保证模型输出更具有生物合理性这一方法具有普适性。在未来森林生长建模工作中，可对深度神经网络模型的激活函数进行建模者本身的经验选择，以得到最佳可用的模型。

5 结论

与传统回归相比，机器学习算法具有对数据分布不作要求、可处理非线性数据、能处理连续和分类变量、预测精度高、数据适应力强等优势，但存在输出可能会偏离生物学规律的问题。本研究提出一个基于Richards 公式的激活函数控制神经网络模型输出，并得到一个输出符合生物学逻辑的树高-胸径神经网络模型。使用Richards 公式的激活函数具有如下优点：1） 输出一定存在一个合理的最大值；2） 配合合理的神经网络结构可使输出一定大于1.3；3） 将传统回归方法拟合得到的参数作为神经网络模型输入，能使神经网络的训练得到先验知识。