巧添辅助线 妙解圆中题

文／王婷婷

若仅根据题中所给图形进行论证或计算，大家有时可能会难以下笔解答。此时，我们若能认真审题，寻找已知与未知的联系，找到添加辅助线的突破口，便可以轻松解决问题。下面，我们就利用圆的特殊性，给大家提供一些添加辅助线的小技巧。

一、连半径，构造等腰三角形

例1如图1，AC为圆O的弦，点B在弧AC上，若∠CBO=58°，∠CAO=20°，则∠AOB的度数为____。

图1

【分析】已知条件和要求的结论之间没有太紧密的联系，但仔细审题后我们会发现，只要连接OC，便可架起条件和结论间的桥梁，从而解决问题。

解：如图2，连接OC。

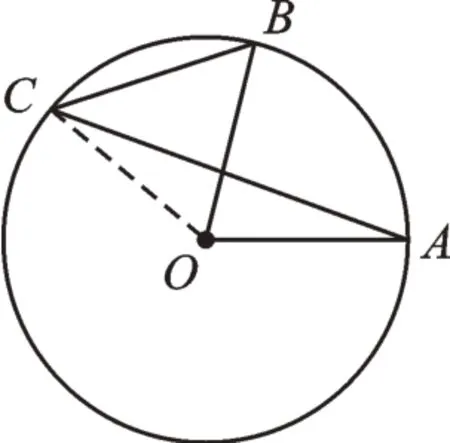
图2

∵OA=OC=OB，

∴∠OCA=∠CAO=20°，∠OCB=∠CBO=58°。

∴∠ACB=∠OCB-∠OCA=58°-20°=38°。

∴∠AOB=2∠ACB=76°。

【点评】在同圆或等圆中，圆的半径相等。因此，我们常常连接半径，构造等腰三角形或全等三角形来解决此类问题。

二、作垂直，构造直角三角形

例2如图3，∠PAC=30°，在射线AC上顺次截取AD=3cm，DB=10cm，以DB为直径作⊙O，交射线AP于E、F两点，求EF的长。

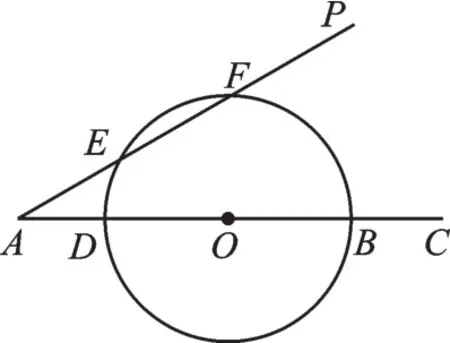
图3

【分析】解决圆中有关弦的问题，常常需要作出圆心到弦的垂线段（即弦心距）这一辅助线。

解：如图4，过点O作OG⊥AP于点G，连接OF。

图4

∵DB=10cm，

∴OD=5cm。

∴AO=AD+OD=3+5=8cm。

∵∠PAC=30°，

∴OG=4cm。

∵OG⊥EF，

∴EG=GF。

∵GF==3cm，

∴EF=2GF=6cm。

【点评】作弦心距，一是利用垂径定理得到平分弦的条件，二是构造直角三角形，利用勾股定理解题。

三、连角平分线，构造相等的角

例3如图5，△ABC中，AB=AC，∠A为锐角，CD为AB边上的高，点O为△ACD的内切圆圆心，则∠AOB=______。

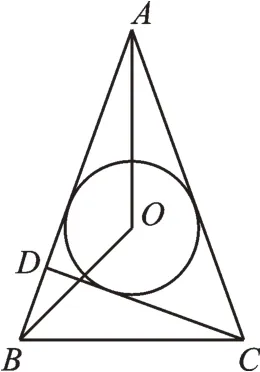
图5

【分析】题中所给条件看似比较少，但仔细分析，我们就能发现内切圆圆心这个条件暗藏玄机。

解：如图6，连接CO。

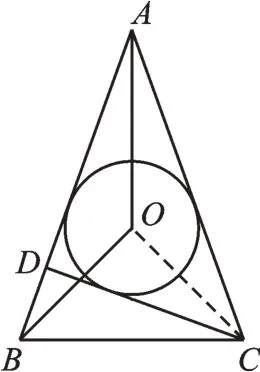
图6

∵CD为AB边上的高，

∴∠ADC=90°。

∴∠BAC+∠ACD=90°。

∵点O为△ACD的内切圆圆心，

∴AO、CO分别是∠BAC和∠ACD的角平分线。

∴∠OAC+∠OCA=45°。

∴∠AOC=135°。

易证△AOB≌△AOC。

∴∠AOB=∠AOC=135°。

【点评】三角形的内心是三条角平分线的交点，抓住角平分线的性质是解此类问题的关键。