基于FFRLS+EKF的特定工况下铅炭电池SOC估计

王 鲁,王 峰,徐利菊,李 玮

(西南林业大学机械与交通学院,云南 昆明 650224)

铅酸电池用于储能领域,存在使用寿命短、维护繁琐及容量小等问题。相比之下,铅炭电池具有较长的使用寿命、良好的充放电性能,在性价比、安全性、低温性能、生产及回收工艺等方面也具有优势[1]。特定工况下,荷电状态(SOC)是电池的状态量,需要通过电流、电压特性和算法来估算。现有算法如开路电压法、电流安时积分法、Kalman滤波算法和Neuronet算法等,都存在精度或者实用性上的问题[2]。申彩英等[3]采用电池开路电压法估计锂离子电池的SOC,误差小于1%,估算精度高,但获取开路电压(OCV)与SOC的关系相对麻烦,不适合在线估计SOC;徐尖峰等[4]通过电流安时积分法结合开路电压和负载电压法来估计电池的SOC,弥补了传统安时积分法的不足,误差在5%以内,但算法在实际应用中较为繁杂。黄磊[5]利用神经网络算法估算锂离子电池的SOC,结果与实际值基本一致,但当SOC小于10%时,估计值与实际值的误差比较明显。

本文作者提出一种基于遗忘因子递推的最小二乘(FFRLS)法+扩展卡尔曼滤波(EKF)算法的铅炭电池SOC估计方法,该方法结合了电池的电流、电压特性,能够克服电流采样误差积聚等问题,可提高SOC估计的精度和稳定性。

1 铅炭电池的等效电路模型

铅炭电池结合了铅酸电池和超级电容器的特点,在发挥超级电容器短时间大容量充放电特点的基础上,保持了铅酸电池高比能量的优势。在铅酸电池负极中加入特种活性炭,可解决硫酸盐化问题,因此电池具有良好的充放电性能及较长的使用寿命[6]。

要准确地估计铅炭电池SOC,首先需要建立等效电路模型。通常模型的RC环节越多,电池的SOC估计越精准,但参数辨识和SOC估计的难度也会相应增加。综合考虑,实验选取二阶的Thevenin模型作为铅炭电池模型,既便于电池内部参数辨识,又考虑了电池极化效应的影响[7]。

图1中:Ut为铅炭电池的端电压;Uoc为开路电压;U1为电阻R1和电容C1两端的电压;U2为电阻R2和电容C2两端的电压;R0是电池的欧姆内阻,由电极原料、电解液、隔膜电阻及各组件的接触电阻构成,与电池的长短、构造和安装工艺等有关,下标charge、discharge分别代表充、放电;R1、R2、C1和C2是体现电池内部极化效应的参数,其中,R1、C1是由于电池内部传荷过程产生的双电层电阻和双电层电容,R2、C2是由电池内部电解液的扩散效应产生的扩散电阻和扩散电容。

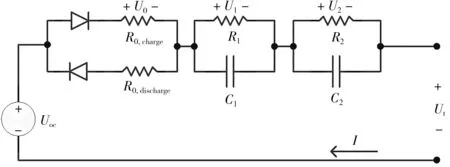
图1 铅炭电池二阶等效电路模型Fig.1 Second-order equivalent circuit model of lead-carbon battery

根据基尔霍夫定律和一阶时域分析,得到以下公式:

式(2)-(3)中:τ为时间常数,τ1=R1C1,τ2=R2C2;e为自然常数;t为时域中的时间;I为充放电电流。

电池的内部参数极易受环境温度和充放电电流的影响,尤其是阻性参数,随温度的升高阻值会减小,且成非线性[8],实际应用中要根据电池的工作状况引入温度修正因子。

2 FFRLS+EKF估算铅炭电池SOC的方法

2.1 遗忘因子递推最小二乘(FFRLS)法

FFRLS是在递推最小二乘法基础上进行改进的一种算法,引入遗忘因子λ。随着数据不断增加,递推最小二乘法会出现“数据饱和”的现象,相对于长期累积的旧数据而言,新数据会被旧数据吞噬,导致算法的修正能力不足[9]。引入遗忘因子λ,可削弱旧数据的信息量,增强新数据的权重,递推过程如式(4)-(6)所示:

式(4)-(6)中:θ(k)为本次待估计值;θ(k-1)为上次的估计值;φ(k)为测量真实值矩阵;y(k)为系统的输出;K(k)为增益矩阵;P(k)为协方差矩阵;I为单位矩阵。

0＜λ＜1,新数据以系数1加权,N个采样周期前的旧数据以系数λN加权,且越早的数据,权重占比越小。当λ=1时,为普通的递推最小二乘法[10]。如果λ选择过大,算法的跟踪能力将会降低;过小,则容易受噪声等因素的影响。λ取值一般为0.95～1.00,实验取0.996。

2.2 扩展卡尔曼滤波(EKF)算法

卡尔曼滤波是解决线性系统问题的一种高效的算法[11],可根据系统的输入输出数据,对系统状态进行最优估计。算法原理如图2所示。

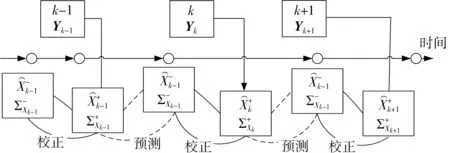
图2 卡尔曼滤波算法原理图Fig.2 Schematic diagram of Kalman filtering algorithm

卡尔曼滤波主要用于处理线性问题,对于非线性问题常使用EKF算法来解决[12]。EKF与标准卡尔曼滤波相比,只存在状态矩阵和输出观测矩阵的差异。完整的EKF算法分为初始化和循环计算两个环节,其中循环计算包括预测方程、状态不确定性方程、卡尔曼增益、校正方程和状态不确定性方程等步骤。

按式(7)、(8)进行初始化。

式(7)、(8)中:E为单位矩阵;为初值状态矩阵;X0为状态初值;为初值的误差协方差值。

按照步骤①-⑤不断进行循环计算。

①预测方程:

式(9)中:为当前状态预测值;f为非线性方程;为前一次的状态值;Uk-1为前一次的系统输入值。

②协方差估计方程:

③卡尔曼增益方程:

式(11)中:Lk为卡尔曼增益;为观测矩阵;∑v为观测噪声。增益越大,修正的力度越大;增益越小,则修正的力度越小。

④校正方程:

式(12)中:Yk为输出观测向量;g为非线性方程。

⑤状态不确定性方程:

2.3 FFRLS+EKF联合算法

为实现铅炭电池模型参数的在线辨识和剩余电量估计,实验采用FFRLS和EKF联合的算法,在线估算铅炭电池的SOC。FFRLS+EKF联合算法流程如图3所示。

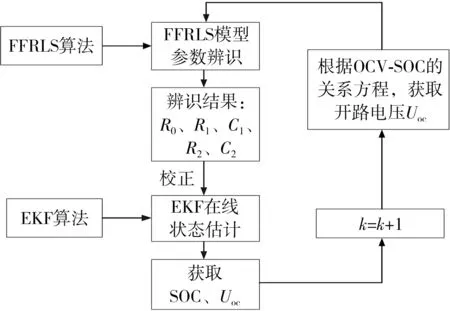
图3 FFRLS+EKF联合算法流程图Fig.3 Flow chart of forgetting factor recursive least squares(FFRLS)+extended Kalman filter(EKF) joint algorithm

首先,利用FFRLS算法对铅炭电池等效模型参数辨识,获取R0、R1、C1、R2和C2,将获取的参数值用于EKF对铅炭电池状态的在线估计。然后,通过模型参数值对EKF状态方程和输出观测方程进行实时校正,获取电池当前的SOC和Uoc。最后,利用OCV-SOC的关系方程更新开路电压,用于下一时刻的等效模型参数辨识。以此类推,可得到任意时刻铅炭电池的等效模型参数和剩余SOC的估算值。

3 FFRLS+EKF在线估计铅炭电池SOC

3.1 实验准备

以6-GFM-17型2 V铅炭电池(昆明产)单体为研究样品,单体容量为16.67 Ah。实验测试仪器为CT-8002高性能电池检测系统(深圳产)。实验环境由ASR-80L-60型可程式恒温恒湿箱(佛山产)提供。特定工况以移动冷库工作状况为例,面向小型移动冷库工况下铅炭电池SOC的在线估计。移动冷库工作状况见图4,且每隔1 h,压缩机运行50 min。

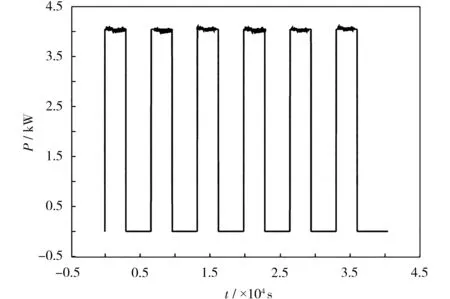
图4 移动冷库的工作状况Fig.4 Working status of mobile cold storage

参考当前移动冷库的工作状况,采用循环间歇放电配合短时间静置(模拟压缩机的工作状态)测试,且放电倍率取0.2C(电流为3.34 A),满足压缩机正常工作下的额定电流,同时,张金龙[13]研究发现,当电池以0.2C恒流放电时,电流系数最接近1,最有利于电池放电曲线的拟合。

为降低实验难度,忽略温度的影响,在恒温25 ℃下,以0.2C对电池放电。为获取SOC与OCV的关系,当电池内部达到动态平衡状态时,以0.2C恒流放电。实验步骤如下。

实验一:首先获取OCV与铅炭电池SOC的关系,在可程式温箱中设置恒定温度25 ℃,选取20只充满电的2.0 V铅炭电池单体,静置24 h,默认电池内部达到动态平衡状态,以0.2C恒流放电至电压下限1.8 V。

实验二:在同样的环境下,以0.2C倍率将20只电池单体充到电压上限2.4 V并静置2 h,将充满电的2.0 V电池单体以0.2C倍率放电50 min,静置1 h,循环6次,每次循环,铅炭电池的SOC减少约2.78%,总测试时间为12 h,设定电池测试系统采样时间为1 s。

3.2 特定工况模拟实验

将铅炭电池置于可程式温箱中,设置恒定温度25 ℃。将铅炭电池与电池测试系统相连,由计算机控制电池测试系统,对电池进行间歇放电操作,同时,通过数据采集卡将测量数据和电池动态特征传输到计算机。

恒流间歇放电工况如图5所示。

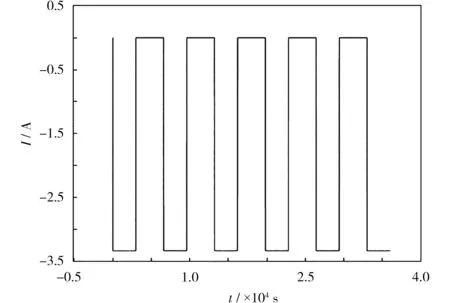
图5 铅炭电池的恒流间歇放电工况Fig.5 Galvanostatic intermittent discharge condition of leadcarbon battery

恒流间歇放电实验中,电池端电压曲线的局部放大图见图6。

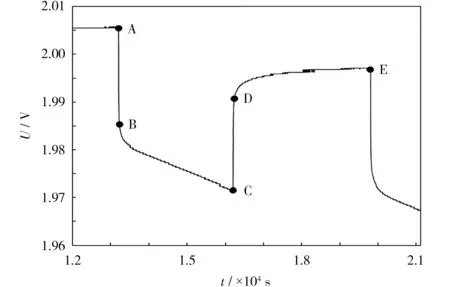
图6 电压的局部放大图Fig.6 Partial enlarged diagram of voltage

图6中,AB段和CD段分别为电池放电开始和放电结束的时间,电压发生突变是由欧姆内阻R0造成的。电池的极化作用,导致BC段和DE段变化相对平缓,电压随电池SOC的减小而降低,导致E点的值明显低于A点的值。

3.3 OCV-SOC关系函数获取

铅炭电池的OCV在等效模型参数辨识和SOC估计中都很重要,通常将OCV-SOC的关系函数作为参数辨识和SOC估计的重要依据。铅炭电池的OCV-SOC拟合曲线见图7。

图7 铅炭电池OCV-SOC拟合曲线Fig.7 Open circut voltage(OCV)-state of charge(SOC) fitting curve of lead-carbon battery

从图7可知,铅炭电池的OCV-SOC曲线基本上呈线性变化。这是铅炭电池性能优势的体现,对辨识电池内部参数、估算SOC等状态量具有重要意义。

OCV-SOC的函数关系式见式(14),是将MATLAB中的Curve Fitting函数工具箱拟合所得公式进行离散化得到的。

式(14)中:Soc(k)为每次的SOC值。

3.4 铅炭电池参数辨识及SOC估计精度验证

实验利用MATLAB软件,根据式(4)-(15)编写算法程序,且遗忘因子λ取0.996,令协方差初始矩阵为P(0)=0.01×E(5,5),导入铅炭电池在恒流间歇放电工况下的数据,通过MATLAB在线仿真。

FFRLS仿真电压和实测电压及二者之间的误差见图8。

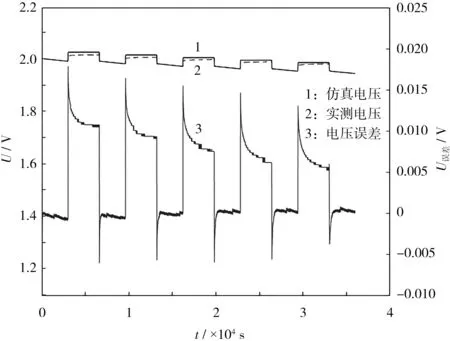
图8 实际电压与FFRLS仿真电压Fig.8 Actual voltage and FFRLS simulation voltage

从图8可知,随着仿真的进行,FFRLS仿真电压逐次逼近于实际电压曲线。由误差曲线看出,仅在搁置区间内,电压误差比较大,但整体误差不超过2%,且逐次减小。实验结果体现出FFRLS算法对数据的追踪能力和收敛性。

R0、R1、C1、R2和C2辨识的结果如图9所示。

图9 铅炭电池参数辨识曲线Fig.9 Parameter identification curves of lead-carbon battery

从图9可知,FFRLS的辨识结果相对准确,参数的辨识数据也较稳定。拟合结果为:R0=0.005 Ω,R1=0.002 Ω,R2=0.001 Ω,C1=364.3 F,C2=318.5 F。

FFRLS+EKF估计的SOC与实际SOC的曲线见图10。

图10 FFRLS+EKF估计的SOC与实际SOC的曲线Fig.10 Curves of SOC estimated by FFRLS+EKF and actual SOC

从图10可知,采用FFRLS+EKF估计的SOC与实际SOC曲线基本重合在一起,且跟随实际SOC值的变化而变化,具有良好线性追踪能力。开始阶段误差比较小,估算的精度高,随着电池放电的进行,电池内部发生化学反应,内部温度也会发生变化,受温度的影响,造成SOC误差有所增加,但最大SOC估计误差不超过0.9%,说明FFRLS+EKF算法满足铅炭电池在实际应用中对SOC估计精度的要求。

4 结论

为实现在线高精度估算铅炭电池的SOC,本文作者选用二阶的Thevenin电路等效模型,对铅炭电池内部参数的辨识和SOC估算结果进行分析。将FFRLS算法和EKF算法结合,特定工况下铅炭电池的SOC估算值精度较高,与实际SOC值的最大误差不超过0.9%。验证了FFRLS+EKF算法对铅炭电池在特定工况下SOC估计的可行性和估算结果的准确性,下一步将FFRLS+EKF联合算法应用到电池管理系统(BMS)中,在工程应用中,实现对铅炭电池SOC的在线估计。