基于经济模型预测控制的燃料电池空气管理

邵 诚,李 浩,朱文超,谢长君

(1.武汉理工大学自动化学院,湖北 武汉 430070; 2.武汉理工大学汽车工程学院,湖北 武汉 430070)

质子交换膜燃料电池(PEMFC)具有启动时间短、能量密度高、工作温度低及无污染等优点,已逐渐成为新能源行业发展的重要方向。过氧比是燃料电池系统的一个重要物理量,与系统的转换效率和寿命密切相关,因此,空气供给管理是PEMFC应用的重要研究部分。

为了研究PEMFC的空气供给管理,J.Pukrushpan等[1]提出一种燃料电池空气供给的九阶模型;K.W.Suh[2]在九阶模型的基础上,简化得到四阶模型,输出量与九阶模型的误差不到3%;I.Matraji等[3]提出一种PEMFC供气系统的次优二阶滑模鲁棒控制方法,并通过硬件在环(HIL)证明了控制器在负荷变化和参数不确定性下的鲁棒性;J.Z.Chen等[4]提出一种基于反馈线性化模型预测控制(MPC)串级驱动的抗干扰控制方案,与比例积分微分(PID)控制相比,在模型参数微调下的控制稳定性的平均绝对误差(AAE)和均方根误差(RMSE)分别减小了26.8%和15.9%;N.Chatrattanawet等[5]设计了一种鲁棒模型预测控制器,能在模型参数不确定的条件下,保证PEMFC系统的稳定性;Z.H.Deng等[6]提出双闭环加权融合的控制方法,在超调量、稳定时间等方面均优于PID控制、自抗扰控制和模糊自整定PID控制。

上述所有控制器有着一个共同的特点,即通过控制燃料电池系统的过氧比来对系统的经济性能进行优化,优化的效果有限,且无法对控制暂态进行经济优化。有鉴于此,本文作者提出一种基于经济模型预测控制(EMPC)的PEMFC空气供给管理算法,使燃料电池运行全程的净输出功率始终处于最大,同时设计两种传统的参考跟踪型MPC控制器进行比较,以验证EMPC控制器的控制效果。

1 PEMFC空气供给系统模型

有许多文献用详细的数学模型对PEMFC的空气供给系统的动态行为进行建模。J.Pukrushpan等[1]提出的PEMFC空气供给系统的九阶状态空间方程模型,十分复杂,限制了在控制领域中的应用;K.W.Suh[2]通过假设,将燃料电池中水蒸气的压力等于饱和蒸汽压力,在保留了系统动态行为的同时,将模型简化到四阶,建立一个面向控制的PEMFC空气供给系统的四阶状态空间模型。

1.1 阴极气流模型

阴极气体流量方程:

式(1)-(2)中:pO2、pN2分别为氧气与氮气的分压;MO2、MN2分别为氧气与氮气的摩尔质量;Vca为阴极体积;t为时间;R为摩尔气体常数;θfc为燃料电池温度;WO2,in、WN2,in分别为氧气和氮气的入口质量流量;WO2,out、WN2,out分别为氧气和氮气的出口质量流量;WO2,react为电堆中反应的氧气质量流量。上述物理量的详细计算公式见文献[7]。

1.2 供气歧管模型

供气歧管动力学模型由式(3)给出:

式(3)中:Vsm为供气歧管体积;psm为供气歧管压力;Ma为空气的摩尔质量;Wcp为空压机质量流量;kca,in为阴极进口常数;pca为阴极压力;θcp为从空压机出来的气体的温度,具体算法详见文献[7]。

1.3 空压机模型

空压机的力矩平衡公式见式(4):

式(4)中:ωcp为空压机转速;Jcp为空压机的转动惯量;τcm和τcp分别为电机的电磁转矩和负载转矩,具体算法见文献[7]。

1.4 状态方程模型

将状态量x定义为式(5),即将x1、x2、x3、x4分别定义为pO2、pN2、ωcp、psm。

将式(1)-(4)整理后,可得到一个完整的四阶状态空间方程模型,如式(6)所示:

式(6)中:系统控制量u为空压机电压U;Ist为电堆电流,作为系统的可测外部扰动;x上方带点表示各状态量对时间的导数;ci(i=1～18)为整理后的常数参数,具体形式可参考文献[7]。

系统的输出y和性能指标z见式(7),即将y1、y2、y3分别定义为PEMFC的电堆电压Ust、净输出功率psm、Wcp;z1、z2分别定义为过氧比λO2、Pnet。

λO2由式(8)得到:

Pnet是电堆功率Pst和空压机消耗的功率Pcp的差值,因此,净输出功率可表示为式(9):

2 基于EMPC的燃料电池进气管理

PEMFC空气供给系统的控制目标是在电堆电流Ist发生改变时,调节空压机的进气流量,保证燃料电池不发生氧饥饿,并使燃料电池的净输出功率Pnet最大。文献[1]将Pnet最大时对应的过氧比(即最优过氧比)始终定为2.0,而I.Matraji等[3]发现,Ist不同时,Pnet最大时对应的过氧比为2.0～2.5,测量出不同Ist下Pnet最大时对应的过氧比,定义最优过氧比,并将这些数据拟合,得到最优过氧比λO2,opt与电堆电流Ist的关系,见式(10)。

2.1 经济模型预测控制原理

传统的MPC中的成本函数,主要由控制输出实际值与参考值的差值的平方构成,通过最小化该成本函数来实现对参考值的跟踪控制。在EMPC中,成本函数由以系统经济性能为指标的非线性经济效益函数组成,通过优化该成本函数,可以提高系统运行全过程的经济性能。

2.2 PEMFC经济模型预测控制器设计

EMPC控制器的设计目标是:在Ist随机变成任意值时,控制器能在满足系统安全约束的条件下,使系统在控制的暂态过程中净输出功率最大,并将系统调节到新的Ist的净输出功率最大时的稳态工作点。

在系统净输出功率表达式前加负号,将最大优化问题转化成EMPC能处理的最小化问题,经济成本函数l表示为:

为了抑制控制量u的变化速率,满足微调系统经济性能的需求,在经济成本函数中添加惩罚项,将经济成本函数定义为:

式(12)中:x(k)为k时刻测量的系统状态量值;N为EMPC控制器的预测时域;x(t|k)为k时刻由x(k)预测的未来第t+1(t=0～N-1)步状态量的值;u(t|k)为k+t时刻(t=0～N-1)控制量的值;u(k) =[u(0|k),u(1|k),…,u(N-1|k)]T;Q为控制量变化的权重;R为控制量分量权重矩阵。

综上所述,PEMFC空气供给管理可变为以下优化问题:

式(14)中:f为由式(6)得到的离散状态方程模型。式(14)中的最后一个约束条件为终端状态约束,保证控制器能控制系统到稳态。uopt(k)为在满足式(14)约束条件的情况下经济成本函数J[如式(13)所示]最小时的最优控制序列,uopt(k) =[uopt(0|k),uopt(1|k),…,uopt(N-1|k)]T。实际控制时,只将控制序列首项uopt(0|k)作用到系统,更新系统状态,并以下一时刻状态量的值再次求解式(13)、(14)的优化问题,得出下一时刻的最优控制量,依次循环反复(如图1所示),算法的收敛性分析详见文献[8]。

图1 经济模型预测控制流程图Fig.1 Flow chart for economic model prediction control

3 仿真与分析

为验证EMPC控制器的经济性能,设计两个过氧比参考值跟踪的MPC控制器用于对比。将过氧比参考值固定为2的MPC控制器定义为MPC-2控制器,将采用文献[3]中的最优过氧比关系式[如式(10)所示]计算得到的最优过氧比为参考值的MPC控制器定义为MPC-d控制器。3种模型预测控制器的预测时域和控制时域均为10,控制器采样时间间隔ts=0.01 s,状态量x和控制量u的初始值和约束均相同,作为系统外部扰动的Ist的变化曲线也相同(如图2所示),PEMFC系统的参数见文献[7]。

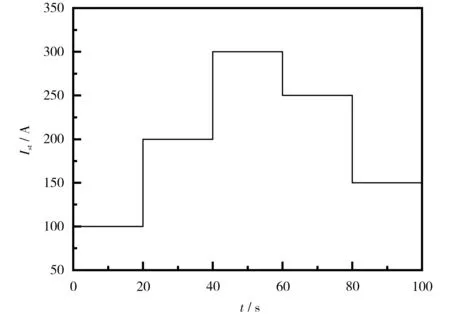
图2 负载电流变化曲线Fig.2 Change curve of load current

图3为空压机控制电压变化曲线。

图3 空压机控制电压变化曲线Fig.3 Change curves of air compressor control voltage

从图3可知,EMPC控制器控制下的空压机电压比其他两种MPC控制器控制下的更激进。这是因为EMPC控制器没有设置过氧比的参考值,仅以系统的Pnet最大化为控制目标,并将Pnet最大化时刻对应的过氧比定为最优过氧比值。从最优过氧比原理上看,该算法得到的最优过氧比很精确,但控制器需要的调控自由度也更高,因此,在成本函数中加入控制量增量惩罚项,来限制EMPC控制器的调控自由度。

采用EMPC、MPC-d以及MPC-2控制器控制的PEMFC系统的净输出功率如图4所示。

图4 PEMFC输出功率曲线 Fig.4 Output power curves of PEMFC

从图4可知,当Ist发生变化时,EMPC控制器始终能驱动系统达到Pnet最大时新的稳态工况。

EMPC控制器控制下系统的Pnet与其他两个控制器控制下的Pnet的差值见图5。

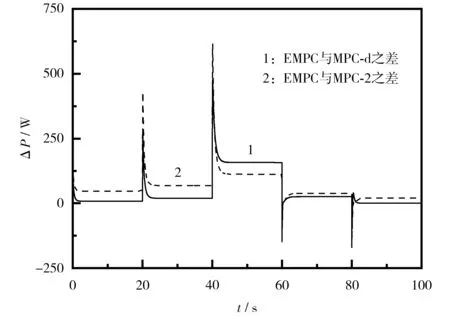
图5 净输出功率差值Fig.5 Difference in net output power

从图5可知,Ist发生变化时,在控制系统从原稳态工况到新的稳态工况的过程(调节暂态过程)中,EMPC控制下的Pnet虽然在某些时刻比另外两种控制器的小,但整个暂态过程中的总净输出功率依然最大。由式(12)可知,这是EMPC控制器对预测时域内的阶段成本函数总和进行优化控制的结果。

EMPC、MPC-d和MPC-2控制器控制下的阴极过氧比曲线变化见图6。

图6 阴极过氧比跟随曲线 Fig.6 Over oxygen ratio following curves of cathode

从图6(a)可知,因为EMPC控制器仅以控制系统Pnet最大化为目标,所以对应的过氧比曲线即为最优过氧比曲线,但与MPC-d控制器和MPC-2控制器使用的参考过氧比有一定的误差。这说明文献[1]、[3]中得到的最优过氧比值并不准确,以这些最优过氧比作控制参考的控制器,无法真正控制系统的Pnet最大化。

由文献[1]、[3]可知,无论是通过实验数据点拟合最优过氧比的表达式,还是将最优过氧比值定为2.0,得到的最优过氧比值与实际最优过氧比值都存在不确定的误差,且误差大小是随机的。如通过实验数据拟合的最优过氧比的表达式,在Ist与实验拟合数据Ist相同或误差很小时,才能保证MPC-d控制器能通过跟踪最优过氧比实现系统的稳态Pnet最大化[如图6(a)中90～100 s时间段内]。当Ist为任意值时,通过该方法计算出的最优过氧比与实际的最优过氧比会存在随机误差,严重影响控制器对系统Pnet的优化效果,甚至出现MPC-d控制器控制下的Pnet低于MPC-2控制器控制的情况(见图5)。想要拟合出准确的最优过氧比表达式,需要采集海量的实验数据,将极大地增加控制器设计前期的工作量。

从图5和图6可知,MPC-d控制器和MPC-2控制器使用的最优过氧比参考值与实际最优过氧比之间的误差对调节Pnet的影响,会随着Ist的增大而增大,即最优过氧比误差相同时,系统输出功率越大,控制得到的Pnet比系统最大Pnet更小。

从图6可知,得益于MPC控制器良好的性能,过氧比跟踪的响应速度和控制效果都很好,但由于无法提供最优过氧比的准确值,导致对系统稳态Pnet的优化控制效果不理想,且与其他两种MPC控制器相比,EMPC控制器在控制暂态的过程中也能最大化系统的Pnet。

综上所述,EMPC控制器构造一个合理的经济成本函数,同时实现了PEMFC空气管理系统控制暂态过程和稳态过程的Pnet优化问题,克服了文献[1]、[3]中最优过氧比与系统实际最优过氧比存在不确定误差的缺点。仿真结果表明,EMPC控制器能将工作在任意电堆电流下的PEMFC系统驱动到净输出功率最大的工况并稳定运行。与MPC-d控制器和MPC-2控制器相比,EMPC控制器在暂态过程中净输出功率分别提高了2.93%和3.82%,在稳态过程中净输出功率分别提高了0.94%和0.67%。

4 结论

本文作者提出一种基于EMPC的PEMFC系统空气供给管理的算法。该算法在继承MPC算法优秀的控制效果和响应速度的前提下,实现了PEMFC系统在暂态和稳态的净输出功率的全局优化。仿真结果表明,暂态过程中净输出功率的提升比稳态过程大很多,暂态过程中最高提高了3.82%,而稳态过程中最高只提高了0.94%。这是因为其他算法也针对稳态的净输出功率进行了优化,但由于算法原理的限制,难以对暂态的净输出功率进行优化。该控制算法能对燃料电池系统全局的经济性能进行优化,且具有极强的抗干扰能力,在燃料电池应用的各领域,均有望带来可观的长期经济效益。