全直流型船舶微电网多时间尺度综合能量管理

周荔丹, 张明珠, 姚钢, 于天佑, 赵敏

(1.上海电力大学 电气工程学院,上海 200090; 2.上海交通大学 电子信息与电气工程学院,上海 200240;3.上海交通大学 船舶海洋与建筑工程学院,上海 200240)

0 引 言

近年来,以综合电力推进系统为标志性技术特征的全直流型船舶,具有可靠性高、机动能力强以及维修成本低等优点而成为未来船舶的重要发展方向[1-2]。相较于传统微网,船舶微网无法在航行过程中与主网交换功率,且由于船舶运行工况处于不断变化的状态,以及叠加的各类航行环境随机变化等因素都会影响船舶运行的可靠性。为了保障船舶能够安全可靠运行,将作为能量缓冲设备的储能系统应用在船舶中[3],且相关船舶综合电力系统能量管理方面的研究内容,已引起了国内外大量学者的广泛关注[4-6]。

电能质量管理方面:文献[7]提出了一种基于节点源荷差分电流的控制策略,在提高响应速度和精度的同时能够降低直流母线电压的波动;文献[8]提出了一种基于直流微网技术的新型能馈系统,能够实现系统源荷储之间功率的合理分配和减小直流母线电压的波动;文献[9]建立了一个集成混合储能系统的全电船舶模型,基于动态下垂控制方法有效改善了电能质量;文献[10]在短时间尺度场景中,在提高全电船舶电能质量的前提下平抑了功率波动;文献[11]提出了一种适用于多微电网互联的不同时间尺度阶梯控制方法,提高了并网的可靠性和安全性;文献[12]提出了一种基于模糊逻辑控制的能量管理系统,在稳定直流侧母线电压的基础上能够根据储能的荷电状态改变其充放电速率,提高了储能的使用寿命。

多目标优化的长时间尺度下负荷经济调度方面:文献[13]提出一种实时模型预测控制能量管理策略,在减小母线电压波动和储能损耗的前提下能解决混合储能系统负载功率波动大的问题;文献[14]提出一种基于优化荷电状态反馈的混合储能能量管理策略,在平抑负载功率和直流波动的前提下延长了储能的使用寿命;文献[15]采用启发式和模型预测控制相结合的混合能量管理算法,能够实现功率的动态平衡;文献[16]提出一种考虑蓄电池寿命损耗的最优船舶储能系统经济调度模型,有效地减小了船舶负荷峰谷差和延长了储能设备的使用寿命,具有较高的经济性;文献[17]提出一种虚拟电阻电容下垂控制和二次荷电状态恢复控制方法用于船舶中压直流系统,有效地缓解了推进负荷和脉冲负荷动态变化引起的功率波动;文献[18]提出一种基于最小使用成本及储能状态平衡的孤岛直流微电网能量管理方法,能够在满足电压稳定和功率平衡的基础上,通过系统底层和顶层之间的协调控制,更好地完成整个系统的能量管理。

由于上述电能质量管理和长时间尺度下负荷经济调度方面的文献没有进行综合能量管理。因此本文提出一种多时间尺度下分层控制的综合能量管理策略,将短期和长期两个时间尺度结合起来,分别提出相应的控制策略,最后通过仿真和算例验证所提策略在短期负荷波动下能够实现直流侧母线电压的稳定和供需功率的平衡,在长期运行下不仅提高船舶微网的经济性,还起到削峰填谷和平滑负荷曲线的作用。

1 本文问题描述

1.1 系统拓扑

船舶微电网系统拓扑结构如图1所示,该系统由发电机、储能单元、各类变换器、推进器以及其他生活负荷共同构成,其中发电单元和储能单元两者共同作用通过输电线路为各类推进器及生活负荷提供电能。

1.2 船舶运行模式

柴电混合动力船舶的驱动动力源由柴油发电机和储能设备共同组成,其运行模式和运行工况种类较多,本文总共考虑了5种船舶运行工况,分别是启动并逐级加速、遇到障碍物转向后继续加速运行、到达安全区域后减速运行、悬浮前进以及低速前行。重点研究以下3种运行模式(具体的能量流动如图2所示)。

1)发电机推进运行模式。

该模式适用于当船舶处于低速前行等负载需求功率较小的运行工况,此时仅靠发电机的出力就可以满足系统的功率需求,储能如果未达上限则对其进行充电,否则其处于备用状态。

2)发电机和储能共同推进运行模式。

该模式适用于当船舶处于加速或负载突增等运行工况,由于发电机的输出特性不能快速响应功率突变,此时应由发电机和储能两者共同作用来满足航行中负载功率的需求。

3)主动减载模式。

该模式适用于发生一些突发状况如果发电机的出力无法满足系统功率需求时,此时负荷若正常工作,将因功率不平衡导致直流母线电压出现较大幅度的下降,在仿真中可以根据负荷的重要程度切除一部分生活负荷以保证重要负荷的可靠供电。

1.3 船舶多时间尺度分层控制

船舶系统结构较为复杂且设备种类繁多,其动态过程的时间跨度较大,包含微秒时间尺度下的开关器件换向过程、毫秒到秒短时间尺度下的电压稳定和功率实时平衡以及分钟到小时长时间尺度下的安全经济运行等等。由于不同时间尺度的复杂程度以及对控制实时性的要求都不同,因此针对该问题,本文从各时间尺度出发,提出了如图3所示的船舶多时间尺度分层控制结构。

本文的研究重点即在该分层控制结构框架下,研究短期大功率推进器接入所带来的负荷功率骤增所带来的电压稳定和供需功率平衡问题以及长期运行下满足船舶可靠性和经济性的要求,搭建了以燃料费用和储能电池使用成本总运行费用最低的运行成本模型,并采取智能算法来迭代优化供电单元的出力。系统关于短期和长期的总体运行策略如图4所示。

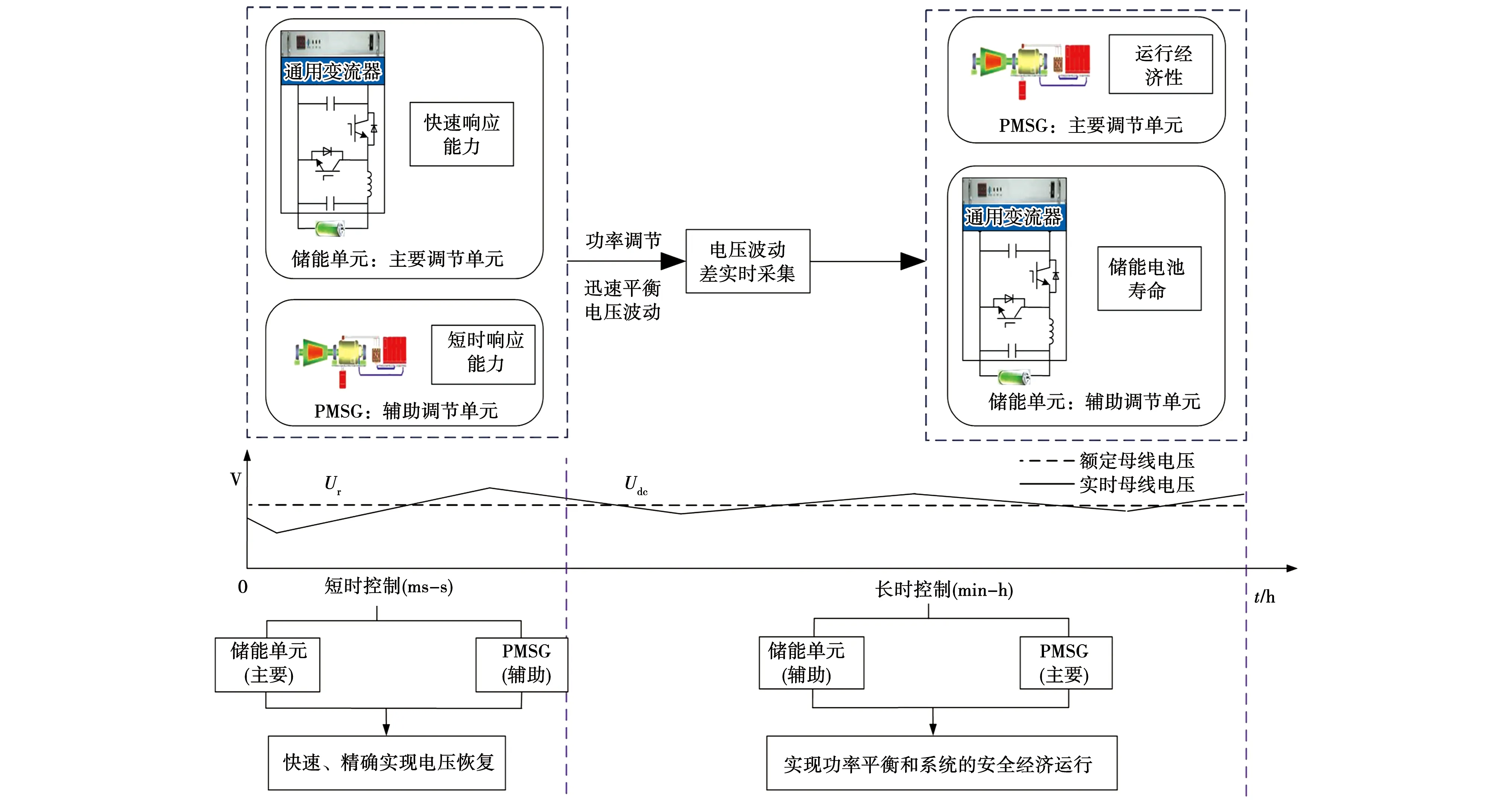
图4 船舶能量管理总体运行策略Fig.4 Overall operation strategy of ship EMS

2 船舶能量管理模型

2.1 系统建模

2.1.1 发电机模型

船舶发电单元一般通过船舶微网将柴油机所产生的电能合理分配给各类负荷,以满足船舶用电的可靠性。对于传统柴油发电机的燃料成本模型[19],本文采用多项式来近似表示柴油能耗特性函数,其能耗特性

F(t)=c1Pdie(t)+c2Pdier(t)。

(1)

式中:Pdie(t)为t时刻单台柴油发电机组输出的平均发电功率;Pdier(t)为单台柴油机组的额定功率;c1和c2是多项式系数。

本文取c1和c2为0.23和0.057 5,则柴油发电机组的燃料成本Cdie(t)可表示为

(2)

式中m为柴油的价格。

2.1.2 储能单元模型

储能充放电模型如下:

(3)

2.1.3 负荷模型

在船舶综合电力系统中,需求侧负载一般可分为以下三类[20]:刚性负荷、可时移负荷、可中断负荷。刚性负荷是维持船舶基本航行的负荷,这类负荷中断将会造成重大的设备损坏,产生很严重的影响,如推进负荷等;可时移负荷指的是短时重复使用的负载,如空调之类的负荷等;可中断负荷指的是偶尔短时使用的负载,如探照灯等之类的负荷。

1)刚性负荷建模。

在自然坐标系下对刚性负荷永磁同步电机进行建模,其磁链方程、转矩方程和推进功率方程[21]为:

ψs=Lssis+ψf;

(4)

(5)

(6)

2)可时移负荷建模。

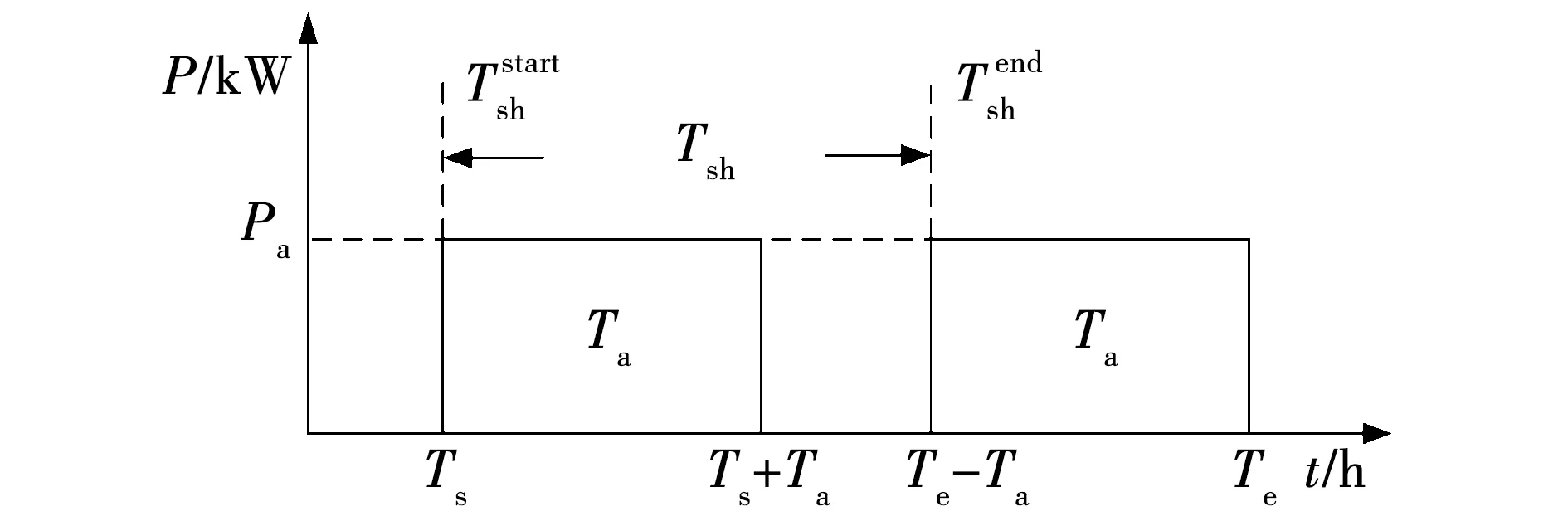
图5 可时移负荷时移区间Fig.5 Times shifting load time shifting interval

可中断负荷与可时移负荷的特性较为类似,这里不再重复,可时移负荷建模如下:

(7)

Ssh(t)≥Ta[Ssh(t+1)-Ssh(t)],

(8)

(9)

式中:Ssh(t)表示负荷的状态,为1表示负荷处于运行中,为0表示设备未运行;Psh为可时移负荷的功率;Esh为可时移负荷的总功耗。

2.2 系统协调控制

2.2.1 永磁同步电机矢量控制

六相永磁同步电机的控制策略采用id=0的转子磁场定向矢量控制策略,该控制的优点在于控制方法简单易实现,可以避免转子永磁体退磁。

基于矢量空间解耦理论得到六相电机的控制模型,模型中包含涉及能量转换的基波dq子空间和z1z2子空间。得到dq轴下的数学模型[21]为:

(10)

式中:ud、uq、ed、eq分别为dq轴上的电压和感应电动势;Rs为定子电阻;id、iq分别为dq轴电流;Leq为等效电感;其中等效电感等于电机定子等效电感与变流器桥臂等效电感之和。

由式(10)可知,ud不仅与id、ed有关,还与iq存在耦合关系,同样uq也是如此,因此在仿真中可采用前馈解耦方法来控制,用来消除电机感应电动势扰动和id、iq之间的耦合。同时对谐波电流采用PI闭环控制来抑制z1-z2子空间的谐波分量在定子绕组产生的损耗,具体控制方程如下:

(11)

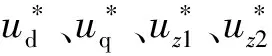
六相PMSM电流iabc与ixyz经过变换之后得到id、iq与iz1、iz2(参见图6所示的矢量控制框图),由于采用的是中性点隔离结构,所以o1-o2子空间中的电气分量不予考虑。将得到的dq轴电流再与速度环输出的电流给定量进行比较,然后经过PI调节之后得到相应的dq电压,最后经过矢量SVPWM模块产生PWM信号来驱动IGBT。

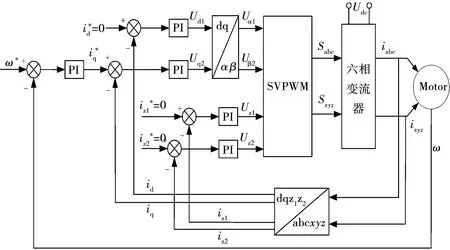
图6 六相PMSM矢量空间解耦控制框图Fig.6 Block diagram of six phase PMSM vector space decoupling control

2.2.2 储能单元控制

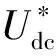
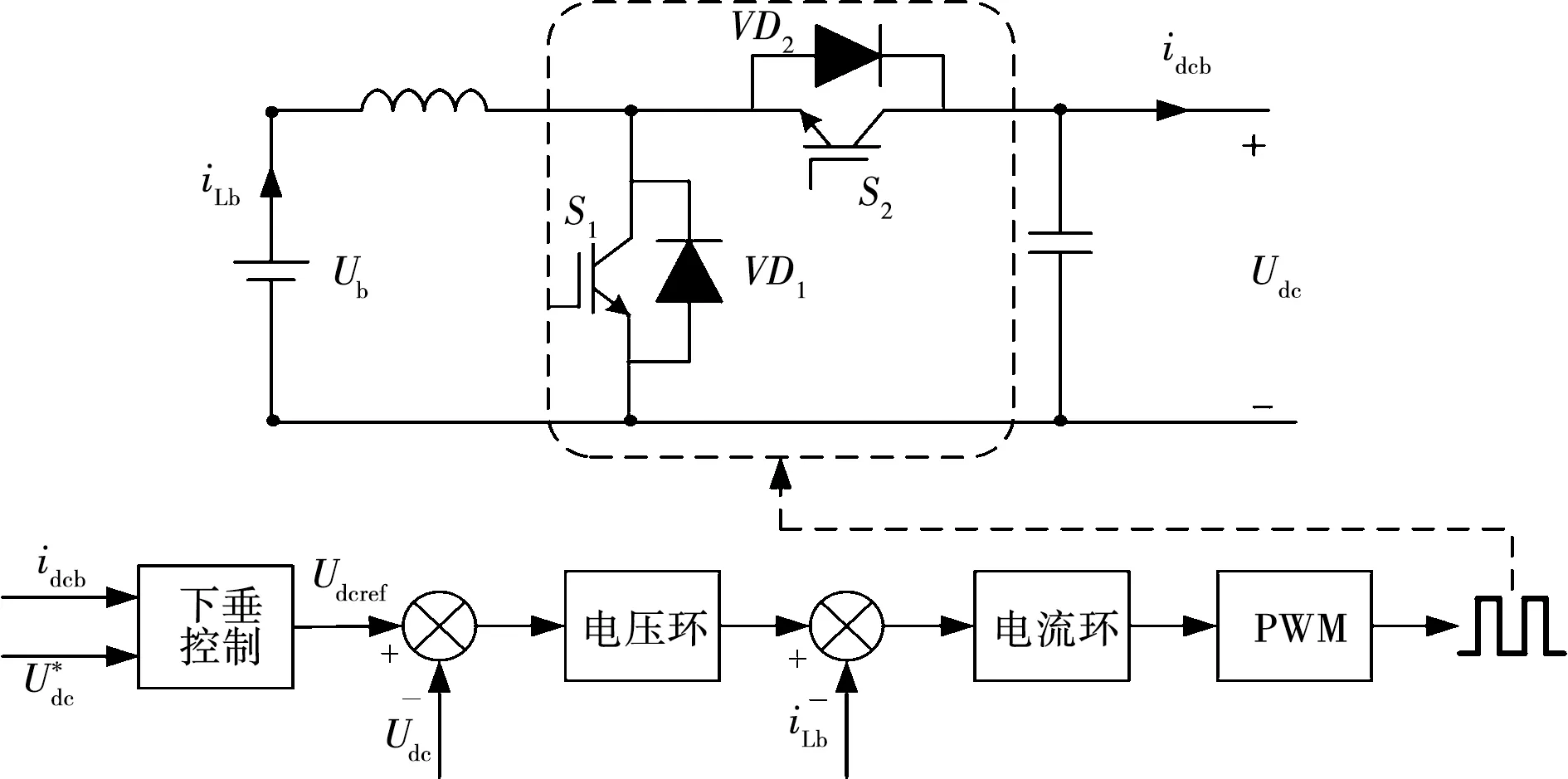
图7 储能单元及其控制框图Fig.7 Energy storage unit and its control block diagram

2.2.3 负荷控制

负荷包括刚性负荷、可中断负荷和可时移负荷,其中刚性负荷的控制策略见图6所示,后两种负荷只需要保证有稳定的电压,采用电压单闭环控制策略就可以实现,其控制结构如图8所示。图8中,Udcref为负荷单元所期望的电压参考值;Ul为负荷电压的实际值。

2.3 系统运行成本函数

1)目标函数。

以船舶微网系统的运行成本最低为目标函数,运行成本主要由燃料费用和储能电池使用成本组成,因此目标函数可表示为

(12)

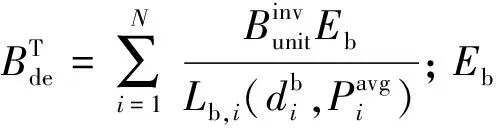
本文为方便分析,采用简化计算,设t时刻储能的折旧成本为

(13)

式中:N为储能电池的循环使用寿命;CB为单组储能电池的价格;n为储能电池的个数;QB为储能电池组的额定容量;ΔWbat(t)为t时刻储能电池的电量变化。

2)约束条件。

①系统功率平衡:

Pdie(t)±Pbat(t)=Pload(t),∀t∈[1,T]。

(14)

式中:Pload(t)为t时刻负荷需求功率的总和;Pbat(t)为t时刻储能电池的输出/吸收功率;T为一天24小时。

②柴油发电机运行功率约束:

0≤Pdie(t)≤Pdier(t),∀t∈[1,T]。

(15)

③储能电池电量约束:

两相邻时刻间储能电池的电量约束为

Wbat(t)=Wbat(t-1)+ΔWbat(t),∀t∈[1,T]。

(16)

式中Wbat(t)为t时刻储能电池的电量。

储能电池存储和释放电量的上下限约束为:

(17)

(18)

④发电机推进运行模式功率约束:

Pdie(t)=Pload(t)-Pbat(t),∀t∈[1,T]。

(19)

⑤主动减载模式功率约束:

Pload(t)>Pbat(t)+Pdie(t),∀t∈[1,T]。

(20)

3 模型分析与求解

3.1 模型分析

本文所提的分层控制结构涉及短期负荷波动下维持直流侧电能质量和系统功率平衡的仿真问题,另外还涉及长期运行下提高船舶微网系统日运行成本经济性的算例优化问题,因此拟采用结构分解的方法将本文所提的多时间尺度分层控制结构分为两层分别进行求解。

3.2 模型分解

本文将1.3节所提出的船舶多时间尺度分层控制结构分解为两部分,分别是采用基于规则的能量管理策略来解决短时间尺度下负荷大功率波动所带来的电能质量和功率平衡问题以及长时间尺度下采用改进型乌鸦搜索算法(crow search algorithm,CSA)对船舶微网系统的日运行成本进行优化。

3.2.1 短期负荷波动下的能量管理

在船舶行驶过程中,由于短期大功率推进器的突然接入将导致系统功率骤增,会对母线电压产生一个短时间的波动,此时如果某供电单元无法响应负荷突变可能会导致电能供应不足,因此有必要研究系统在短时间尺度下的控制策略。

针对负荷的短期波动采用基于规则的能量管理策略。该策略是目前应用最为广泛的一种方式,具有设计简单,鲁棒性强,技术成熟等优点。该方法以推进电机负载转矩的变化来模拟系统处于不同的运行工况,并根据要实现的目标、系统当前的需求功率以及各设备的运行情况,来完成功率的分配。具体的规则如图9所示。

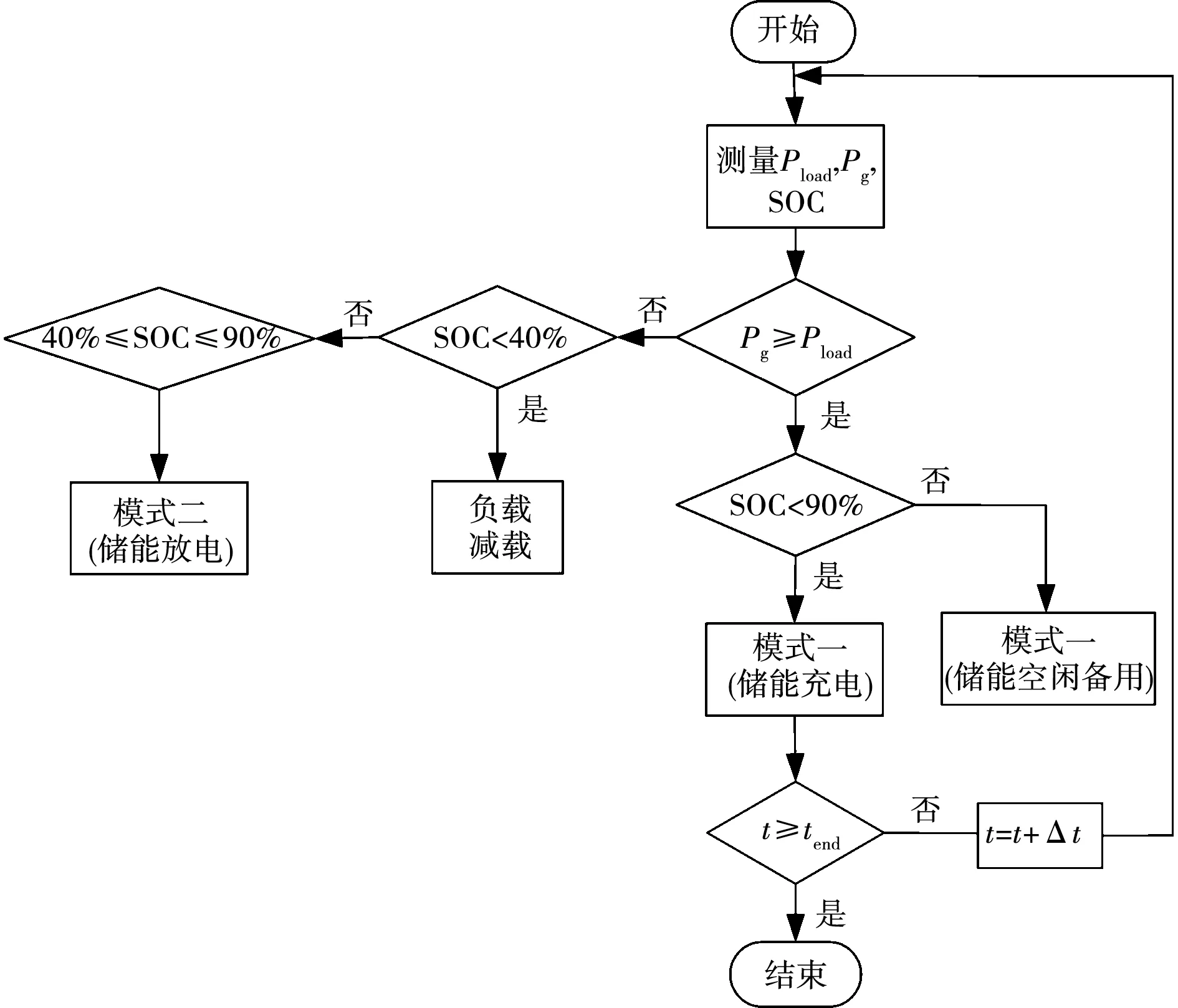
图9 基于规则的功率控制流程图Fig.9 Power control flow chart based on rules

3.2.2 采用改进型CSA算法的模型求解

针对船舶长期处于孤岛运行方式,在满足船舶供需能量平衡的基础上,基于船舶电力系统长期运行经济性的要求,采用改进型CSA算法对系统的运行成本函数进行优化。

1)算法原理。

CSA是一种基于种群间觅食行为的新型智能优化算法,主要通过从给定的求解空间中的所有可行解中找到满足约束条件的最优解,其寻优机制简单和可操作性强,但是该算法在解决复杂、非线性优化问题时容易处于局部最优状态,且收敛速度较慢。因此针对该算法的缺陷,本文提出一种改进型CSA算法,并将其应用到船舶微电网系统中求解日运行成本最低的问题。

①传统CSA算法。

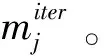
情况1：当认知概率AP小于所生成的随机数ri时,说明个体j并不知晓被跟踪,则最终个体i会找到个体j隐藏食物的地点;

情况2：当认知概率AP大于所生成的随机数ri时,说明个体j已知被跟踪,为了使隐藏食物的地点不被发现,个体j会随机飞往空间中的其他位置。

上述两种情况下的位置更新公式如下:

(21)

②基于改进型CSA算法。

为了使得算法的搜索空间更大,同时避免陷入局部最优的情况,本文采用改进型CSA算法,相较于传统CSA算法做了以下两点改进:

(a)引入权重系数。

引入权重系数来对个体的位置更新公式进行修正,借此拓宽个体的搜索空间,这样更有利于搜索到全局最优解,从而降低个体落入局部最优的概率,新的位置更新公式如下:

(22)

(23)

式中:rgbest为当前迭代过程中的最优解;witer为第iter次迭代之后的惯性权重;itermax为最大迭代次数;wmin、wmax分别为惯性权重系数的最小值和最大值。

(b)引入随机扰动因子。

当检测到个体位置停止更新时,说明算法可能已经陷入局部最优解(本文设置函数迭代到第150次时,陷入局部最优),此时为了个体能够跳出当前局部最优,引入随机扰动因子,使算法可以进入一个更好的寻优空间,从而找到全局最优解。具体计算公式如下:

(24)

改进型CSA算法和传统CSA算法对比而言,只有每次迭代的惯性权重系数是不一样的,其他的参数如最大迭代次数itermax,种群数量N,飞行长度f1、认知概率AP以及变量个数pd(指的是个体i和个体j两个变量)是初始化的时候就已经定义好的,两者是一样的。详细参数见表2所示。

2)算法执行步骤。

综上所述,本文采用的改进型CSA算法具体执行步骤如下:

①初始化各种可调参数,并针对所研究的问题来完成相应目标函数的定义;

②初始化个体的位置及其记忆位置,且假设个体的初始位置为其记忆位置;

③根据目标函数来计算个体记忆中的最佳位置;

④判断算法是否陷入局部最优,如果是,则转到步骤⑤,如果否,将按照式(22)引入权重系数来对位置更新公式进行修正;

⑤陷入局部最优时,按照式(24)引入随机扰动,使得算法可以跳出当前局部最优的状态;

⑥重新计算个体的适应度函数,并更新相应的记忆位置和最优位置信息;

⑦重复以上步骤③～⑥,直至达到设置的最大迭代次数时终止循环操作;

⑧输出个体在更新过程中所搜索到的最优目标值。

4 短时仿真与实验分析

4.1 仿真参数

本文针对图1船舶微电网拓扑结构图在MATLAB/Simulink中搭建了相应的仿真模型,系统各个部分的参数如表1所示。

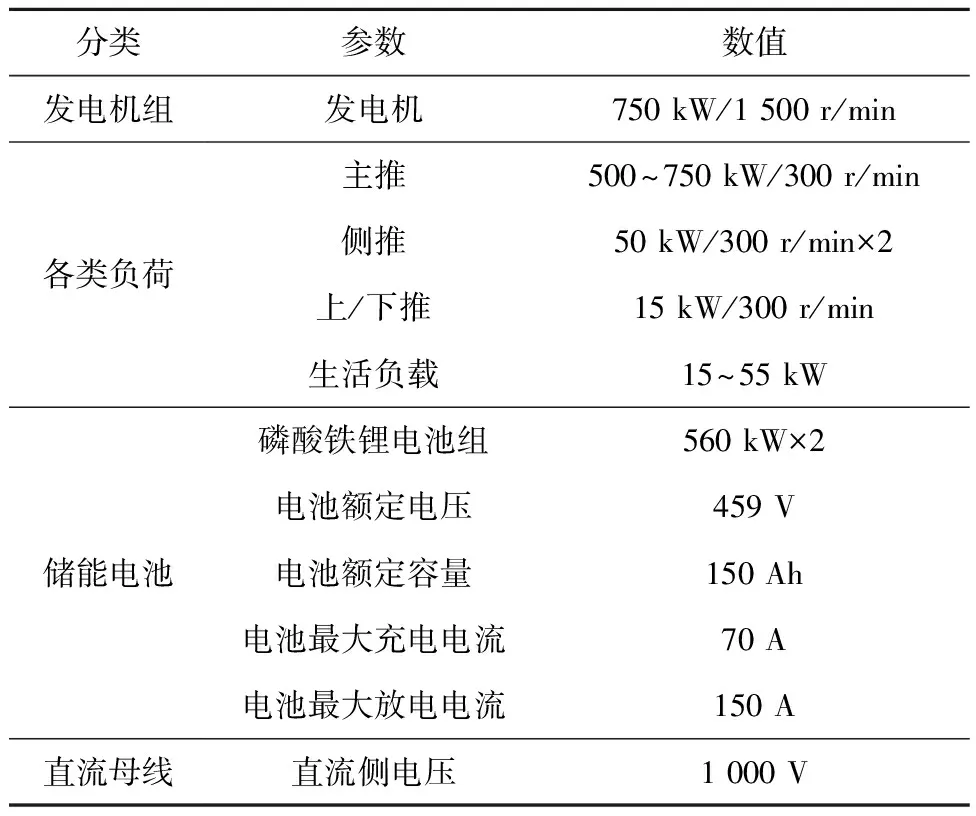
表1 系统仿真模型参数Table 1 Parameters of system simulation model

4.2 仿真结果分析

短时间尺度的仿真时间设置为4.2 s,在该时间尺度下,将发电机推进运行模式和主动减载模式合并为模式一,相关的仿真结果如图10所示。图10(i)中的Δ|U|为电压的偏移率,计算不同曲线的电压最大偏移量和直流侧电压基准值两者之间的比值,这样就可得到不同曲线的电压偏移率。

图10(a)～图10(i)是系统处于不同模式下的仿真结果。在模式一储能单元处于空闲备用状态时,其中考虑到图10(a)模式一在1.8～2.4 s时间段内仅靠发电机的出力无法满足系统推进负荷和生活负荷的功率需求。通过仿真结果图10(i)可以看出在不进行任何操作且无储能的情况下,电压偏移率为3.5%,在无储能但进行减载操作之后,电压的偏移率下降到1.8%,此时若储能参与系统调节,则电压偏移率进一步降低到1.4%,最后在储能参与调节的基础上并加上基于规则的能量管理策略,电压偏移率仅为1.2%。

通过以上对比,可以明显地看出在系统处于短时过负荷工况下,进行负荷减载操作或由储能提供超出发电机最大出力的那部分功率需求,都能有效地减小直流侧电压的波动,从而提高系统的稳定性。

由上述仿真结果可以看出,系统在模式一和模式二不同工况下都能实现供需功率的平衡和直流侧电压的稳定。

4.3 实验结果分析

为了验证所提方法的有效性,本文搭建了如图11所示的实验平台。由于示波器探头数目有限,因此采用一根探头分别对不同模式不同工况下的直流侧母线电压波形进行观察。

由于仿真时系统刚性负荷中推进电机的功率参数较大,实验时系统刚性负荷的参数和仿真有所区别,具体参数如表2所示。

当系统处于模式一无储能状态时,系统运行稳定后的直流侧母线电压实验波形如图12(a)所示,通过示波器可以读出,其电压偏移率分别为6.6%和9.4%;对比于图12(b)系统处于模式一有储能状态时直流侧母线电压的实验波形图可以看出,其电压偏移率分别由6.6%降为6.4%、9.4%降为6.3%;当系统处于模式二有储能且采用基于规则的能量管理策略时,系统运行稳定后的直流侧母线电压实验波形如图12(c)所示,通过示波器可以读出,其电压偏移率进一步下降为4.2%和3.5%。实验时不同模式不同工况下直流侧母线电压的偏移率对比仿真结果图中的电压偏移率存在一定的误差,但仍然可以验证本文所采用的能量管理策略能够有效地改善由于负荷负载骤增或突降所带来的电能质量问题,与前面章节的仿真分析一致。

图12 不同模式不同工况下的直流侧母线电压实验波形Fig.12 Test waveform of DC side bus voltage under different modes and working conditions

5 长时算例分析

5.1 参数设置

本文配备1台柴油发电装置,其额定功率为750 kW,使用价格约为6.0元/L的180CST燃料油;磷酸铁锂电池某一品牌的单价在1 400～1 600元/(kW·h),充放电循环次数约为2 480次左右,由于仿真中储能的容量是根据项目需求,其容量过大,在此只取8个储能单元,约560 kW。系统的时间间隔为1 h,总时长为24 h进行算例仿真。

在长时间尺度下,本文采用改进型CSA算法对所提的运行成本函数进行求解,并与遗传算法(genetic algorithm,GA)、粒子群算法(partricle swarm optimization,PSO)以及传统的CSA算法得到的优化结果进行对比,其中改进型CSA算法的相关参数如表3所示。

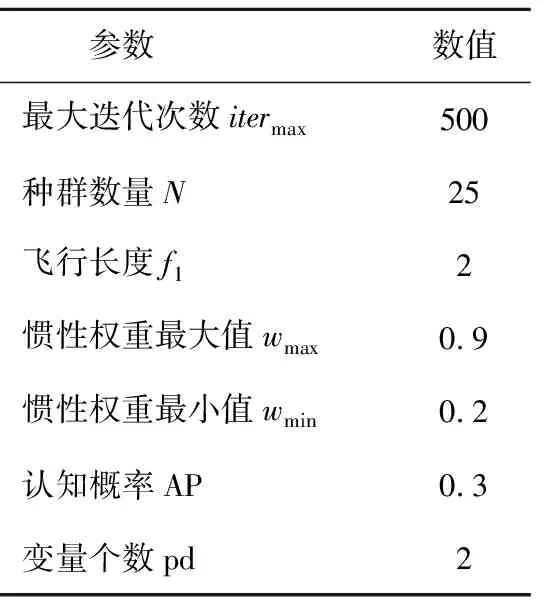
表3 改进型CSA算法参数Table 3 Parameters of improved crow search algorithm

5.2 算例结果分析

采用不同的优化算法进行优化后各部分运行成本对比见表4所示。

由表4的运行成本对比可以看出,采用改进型CSA算法无论是收敛速度还是寻优能力均优于其他的对比算法,其中船舶微网的总运行成本相较于GA算法、PSO算法和CSA算法依次下降了21.3%、17.2%和4.4%,提高了船舶运行的经济性。

由图13(c)可以看出优化之后的总负荷需求在8:00-16:00之间需求减少,在0:00-7:00之间需求增加。可见考虑可中断负荷和可时移负荷后能减小负荷峰谷差,使得负荷曲线更加平滑,从而起到削峰填谷的作用,此外在16:00-24:00之间发电机的出力有所下降,使得系统更加清洁环保。

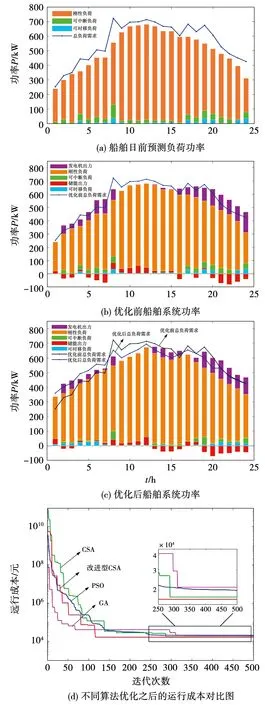
图13 船舶长期仿真结果图Fig.13 Long term simulation results of ship

6 结 论

本文对船舶微电网综合电力系统不同时间尺度优化调度进行了研究,提出了一种多时间尺度下的分层控制综合能量管理策略,构建了基于短期负荷波动下的微网仿真模型和基于长期运行下的系统运行成本优化模型,具体结论如下:

1)通过对比系统在不同模式以及不同运行工况下的仿真结果:在同样配备储能系统的基础上采用基于规则的能量管理策略,使得系统在不同运行模式切换时电压偏移率最大仅为0.4%,有效地改善了电能质量;

2)长期运行下提出改进型CSA算法对系统的燃料和储能电池总运行成本进行优化,通过不同算例的对比优化结果:该改进算法相比于其他算法不仅可以使得负荷曲线更加平滑,起到削峰填谷的作用,而且具有一定的经济效益。