新型双层半插入式交替极永磁电机的解析建模
倪有源, 张亮, 钱威
(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)
0 引 言
无刷直流/交流永磁电机因结构简单、功率密度高及效率高等优点,在各个领域应用十分广泛[1-2]。与传统的表面插入式永磁电机相比,交替极永磁电机在保证较高功率密度的同时,可以节省永磁材料,降低制造成本,具有广泛的应用前景[3]。
国内外学者对交替极永磁电机进行了广泛的研究。文献[4]建立了外转子交替极电机的通用解析模型,并计算了其电磁性能。文献[5]分析了交替极磁通反向永磁电机,与传统电机相比,该电机可减少漏磁,从而提高了感应电动势和电磁转矩。文献[6]分析比较了传统内置式永磁同步电机与内置式交替极永磁同步电机的电磁性能。文献[7]建立了开口槽交替极电机空载磁场、负载磁场和电枢反应磁场的解析模型,由于不对称性,气隙磁场中的偶次谐波含量较高。由于交替极电机具有非对称气隙磁场,文献[8]研究了不同极槽配合下偶次谐波对空载感应电动势、齿槽转矩和电磁转矩波动的影响。
对永磁电机的精确建模是获得其电磁性能及进行优化设计的前提。文献[9-10]采用等效磁路法分别研究了内置式永磁电机的电感参数和磁化特性。文献[11-12]采用等效磁网络法对直线永磁电机进行了建模分析。文献[13-14]基于数值法研究了不同转子磁路结构内置式永磁电机的转矩特性。文献[15]采用保角变换法建立了开槽永磁电机的解析模型,计算了气隙比磁导。相比以上方法,子域模型法不仅计算精度高,而且计算时间少,非常适合分析电机电磁场。文献[16-18]建立了表贴式开口槽电机空载磁场解析模型,计算了气隙磁密、反电动势和电磁转矩,但未考虑实际电机定子齿尖的影响。半开口槽电机比开口槽电机多了槽口子域,使得方程的求解变得更为复杂。文献[19]采用子域模型法研究了表贴式开口槽永磁电机的电磁性能,并与有限元的结果进行了对比。文献[20-21]建立了表面插入式半开口槽电机的二维子域模型,可以计算任意极槽比、不同磁化方式的永磁电机的磁场分布。文献[22]基于子域模型法研究了一种表面插入式半开口槽电机的磁场分布和运行参数。为降低电磁转矩脉动和永磁体涡流损耗,文献[23]提出一种表贴式分段Halbach永磁结构,利用二维解析建模,获得了两种不同磁极结构的电磁性能。
由于交替极永磁电机具有不对称性,导致气隙磁场和感应电动势的波形中谐波含量较高。与表贴式永磁电机相比,交替极永磁电机的电磁转矩脉动较大。因此,本文在交替极电机的基础上,提出了一种新型双层半插入式交替极永磁结构,该结构的内层永磁和外层永磁分别为交替极和表贴式,削弱了交替极永磁电机不对称性对电磁性能的影响。在电机的分析方法中,子域模型法不仅计算精度高、计算速度快,而且每个变量的物理意义明确,非常适合对该电机进行解析建模。
本文首先给出双层半插入式交替极永磁电机的结构。然后采用二维子域模型法对其进行建模,利用微分方程和边界条件建立矩阵方程,并求解获得磁场分布以及电磁性能。计算结果表明,与传统的表面插入式电机相比,新型电机具有更高的电磁转矩。最后,利用有限元仿真结果验证解析模型的有效性。
1 新型电机结构
传统表插式转子结构如图1(a)所示。新型双层半插入式交替极电机的转子结构如图1(b)所示。采用双层磁极结构,内层为交替极磁极,外层为表贴式磁极,内外层永磁都采用径向充磁。
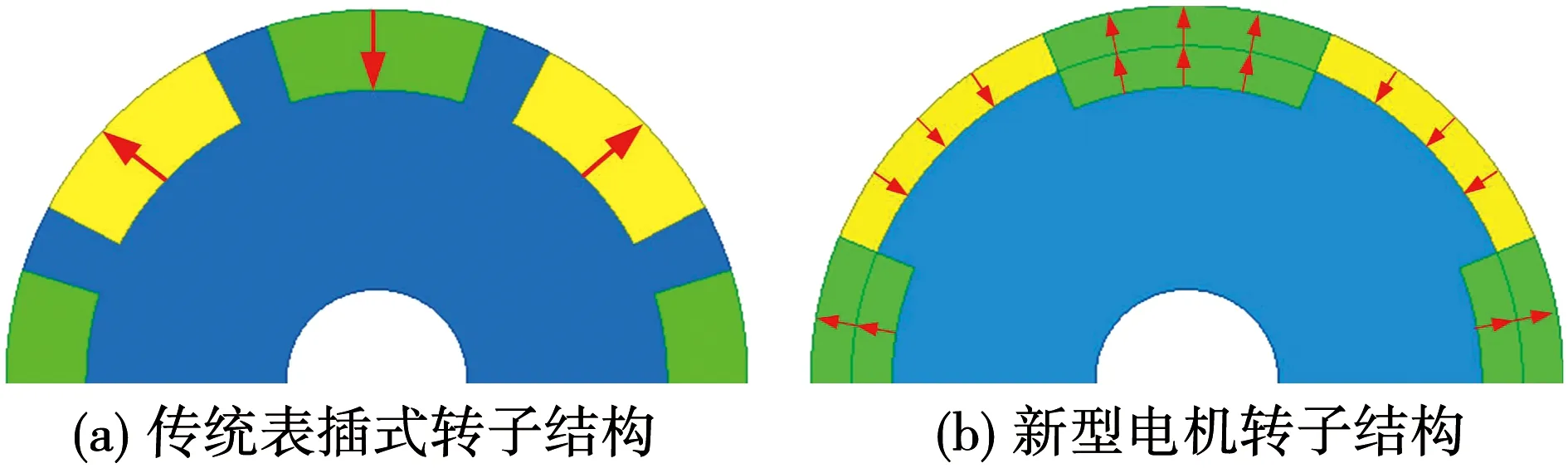
图1 两种电机转子结构图Fig.1 Rotor structures of two machines
新型电机的定转子结构图如图2所示。为方便求解,新型双层半插入式交替极电机定子槽为理想的带齿尖的扇形结构。图中:ξ1为扇形定子槽对应圆心角的弧度;ξ2为扇形定子槽口对应圆心角的弧度;ξ3为转子槽对应圆心角的弧度。为便于计算,将图中的定转子位置设为初始位置。此时转子槽中心线与扇形槽中心线重合,定义该转子槽和定子槽为第1个转子槽和第1个定子槽。转子槽序号以逆时针为正方向,依次为第2个转子槽,…,第s个转子槽;定子槽序号以逆时针为正方向,依次为第2个定子槽,…,第i个定子槽;R1为内层磁极内半径,R2为内层磁极外半径,R3为外层磁极外半径,R4为定子内半径,R5为定子齿尖外半径,R6为定子槽外半径;θi为第i个定子槽中心线与第1个定子槽中心线之间的夹角;θs为第s个转子槽中心线与第1个转子槽中心线之间的夹角。θi和θs的表达式分别为:
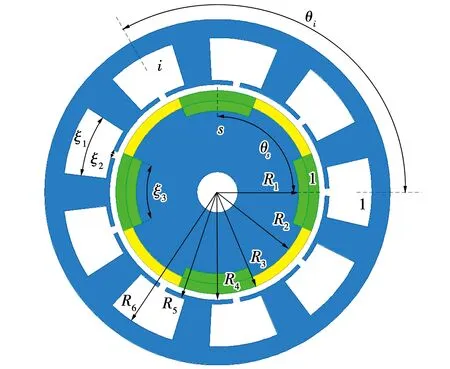
图2 新型电机定转子结构图Fig.2 Stator and rotor of proposed novel machine
(1)
式中:Nr和Ns分别为电机转子槽和定子槽的数量;θ0为转子相对于初始位置的位置角。
2 解析建模分析
以新型双层半插入式交替极永磁电机为对象,基于子域模型法进行磁场分析,需要如下假设:a)定子转子的铁心磁导率为无穷大;b)永磁体的相对磁导率μr=1.05;c)只考虑二维模型;d)定子槽和定子槽口均为理想的径向扇形。
将新型电机的求解域分为:定子槽、定子槽口、气隙、外层永磁和内层永磁共5个子域。采用子域模型法,需对各子域矢量磁位A的z分量建立偏微分方程。在二维极坐标系中,磁密的径向分量、切向分量与矢量磁位的关系可以表示为:
(2)
文献[7]定义了一类方程,该方程对偏微分方程通解的表达式进行了谐波分量系数的缩放,从而能够化简运算。该方程定义为:
(3)
接下来对新型电机各子域的方程进行求解。
2.1 槽子域磁场分析
对于有Ns个定子槽的新型电机,共有Ns个槽子域。设二维极坐标下iA1(ρ,θ)为第i个槽内矢量磁位A的z分量,其中i=1,2,3,…,Ns。当线圈中电流为0时,第i个槽子域内拉普拉斯方程的通解为
(4)

iA1(ρ,θ)=iW1+iX1lnρ+
(5)
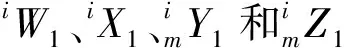
(6)
式中m为定子槽域矢量磁位的谐波阶数。
2.2 槽口子域磁场分析
由新型电机的结构图可得,对于有Ns个槽的新型电机,其槽口子域共有Ns个。设二维极坐标下jA2(ρ,θ)为第j个槽口子域内的矢量磁位A的z分量,其中j=1,2,3,…,Ns,那么在线圈中电流为0时,对第j个定子槽口子域内拉普拉斯方程的通解使用分离变量法求解,同时对各系数进行缩放,可得槽口子域矢量磁位的通解为
jA2(ρ,θ)=jW2+jX2lnρ+
(7)
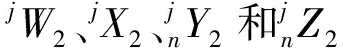
(8)
(9)
2.3 气隙子域磁场分析
由图2可得,该求解域是位于R3与R4之间的环形区域。设二维极坐标下A3(ρ,θ)为气隙子域中矢量磁位A的z分量,通过求解该子域内的拉普拉斯方程,可得其通解为
A3(ρ,θ)=a3+b3lnρ+
(10)
与槽子域和槽口子域不同,气隙子域为一连通的环形区域。根据安培环路定律可得,该通解不含有直流分量。于是将式(10)进行化简,其解的最终形式为
(11)
式中:kW3、kX3、kY3和kZ3分别为气隙子域矢量磁位的直流分量系数和谐波分量系数;k为气隙域矢量磁位的谐波阶数。
2.4 外层永磁子域磁场分析
由图2可得,该求解域是位于R2与R3之间的外层磁极区域。设二维极坐标下A4(ρ,θ)为外层永磁子域矢量磁位的z分量,其偏微分方程和域范围为:
(12)
式中Mρ和Mθ分别为永磁体磁化强度的径向分量与切向分量。
对于径向磁化的永磁体,其磁化强度的径向分量与切向分量为:
(13)
式中:
(14)
利用非齐次偏微分方程解的性质,由安培环路定律,采用分离变量法,可得其解为
(15)
对该解进行化简,可得其解的最终形式为
(16)
式中:uW4、uX4、uY4和uZ4分别为外层磁极子域矢量磁位的直流分量系数和谐波分量系数;u为外层磁极子域矢量磁位的谐波阶数;函数Fu(ρ)为:
(17)
2.5 内层永磁子域磁场分析
由新型电机的结构图可得,对于有Nr个转子槽的新型电机,其内层永磁子域共有Nr个。设二维极坐标下sA5(ρ,θ)为第s个内层永磁子域内的矢量磁位的z分量,其中s=1,2,3,…,Nr。当线圈电流为0时,在该子域内sA5(ρ,θ)的偏微分方程和域范围为:
(18)
式中sMρ和sMθ分别为永磁体磁化强度的径向分量与切向分量。对于径向磁化、极弧系数为1,且置于转子槽内的永磁体,sMρ和sMθ为:
(19)
式中:
(20)
(21)
使用分离变量法,考虑非齐次偏微分方程的解的性质以及系数缩放,可得其解的最终形式为
(22)

(23)
(24)
式中v为内层永磁子域矢量磁位的谐波阶数。
3 谐波系数求解
利用在ρ=R1、ρ=R2、ρ=R3、ρ=R4、ρ=R5以及ρ=R6共6个位置处的边界条件建立矩阵方程,求解各子域矢量磁位中的各谐波分量系数。考虑到在ρ=R1和ρ=R6处,可对矢量磁位进行化简,因此,首先对这两处的边界条件进行求解,然后再求解其他位置。
3.1 在ρ=R1处的边界条件分析
由图2可得,ρ=R1为内层永磁子域与转子铁心的交界面,在此处有
(25)
将式(22)代入式(25),可以解得
(26)
(27)
将式(26)代入式(22),得内层永磁子域的矢量磁位为
(28)
3.2 在ρ=R6处的边界条件分析
由图2可得,ρ=R6为定子槽子域与定子槽底的交界面,此处满足
(29)
将式(5)代入式(29),可以解得:
iX1=0;
(30)
(31)
将式(30)和式(31)代入式(5),可得槽子域的矢量磁位为
(32)
3.3 在ρ=R5处的边界条件分析
由图2可得,ρ=R5为定子槽子域与定子槽口的交界面,根据径向气隙磁密连续的边界条件,可得:
(33)
显然,定子槽口与定子槽为一一对应关系,因此在计算过程中,始终有i=j。根据傅里叶级数的性质和边界条件式(33),在槽口子域矢量磁位的直流分量系数和谐波分量系数分别为:
F1(m);
(34)
(35)
式中:
(36)
F2(m,n)=
(37)
在ρ=R5处的另一边界条件为切向磁场强度连续,可表示为
(38)
由式(38),根据傅里叶级数的直流分量系数和谐波分量系数的性质,可得:
jX3=0;
(39)
(40)
于是可得,式(34)、式(35)、式(39)以及式(40)为谐波分量系数。由于后续各边界条件的分析求解过程类似,仅给出边界条件和得到的谐波分量系数方程,求解过程将不再赘述。
3.4 在ρ=R4处的边界条件分析
由图2可得,ρ=R4为定子槽口与气隙的交界面,满足的两个边界条件为:
(41)
同样对矢量磁位函数进行傅里叶分解,可得其直流分量系数和谐波分量系数分别为:
(42)
(43)
(44)
(45)
式中:
(46)
(47)
F5(n,k,j,ξ2)=
(48)
F6(n,k,j,ξ2)=
(49)
3.5 在ρ=R3处的边界条件分析
由图2可得,ρ=R3为气隙区域和外层磁极区域的交界面。由于两区域均为环形区域,无需进行傅里叶分解,只需将对应的各阶谐波分量系数代入边界条件运算即可。在计算中,始终有k=u,在此处的边界条件为:
(50)
将矢量磁位的表达式代入式(50),可得:
Fu(R3)sin(uθ0);
(51)
Fu(R3)cos(uθ0);
(52)
(53)
(54)
3.6 在ρ=R2处的边界条件分析
由图2可得,ρ=R2为外层磁极区域和转子槽的交界面。其边界条件为:
(55)
同样对矢量磁位函数进行傅里叶分解,可得其直流分量和谐波分量系数的方程为:
Fu(R2)sin(uθ0)]F3(u,s,ξ3)+
Fu(R2)cos(uθ0)]F4(u,s,ξ3);
(56)
sin(uθ0)]F5(v,u,s,ξ3)+
Fu(R2)cos(uθ0)]F6(v,u,s,ξ3);
(57)
(58)
(59)
联立式(26)、式(27)、式(30)、式(31)、式(34)、式(35)、式(39)、式(40)、式(42)~式(45)、式(51)~式(54)以及式(56)~式(59)共计20组方程,即可求解获得各区域中矢量磁位的直流分量系数和谐波分量系数。然后将气隙区域中的矢量磁位A3(ρ,θ)代入式(2),可求解得出新型电机的气隙磁场。
4 电磁性能比较和有限元验证
新型电机定子采用集中绕组,即绕组的节距为1。对于任意的转子位置,每个线圈交链的磁链可以由线圈两个有效边的平均矢量磁位之差计算,然后由磁链的微分可以获得空载感应电动势。一个线圈的磁链可以表示为:
ψx=ψx+-ψx-;
(60)
(61)
式中:L为轴向长度;Nc为线圈匝数;S为每个槽的面积。
每相绕组有Nλ个线圈串联构成,每相串联匝数为N=NcNλ匝,那么该相总磁链为
(62)
于是,该相的空载感应电动势为
(63)
式中ω为电机的角速度。
三相电机的电磁转矩表达式为
(64)
式中:EA,EB,EC是三相感应电动势;iA,iB和iC是三相对称的电枢电流。
以下比较定子结构完全相同、8极9槽两种电机的电磁性能。并且这两种电机永磁用量、永磁外半径R3及内半径R1也相等。其中,传统表面插入式永磁电机的永磁占比为0.76;新型电机外层永磁极弧系数为1、内层永磁占比为0.5。表1给出了新型电机的主要结构参数。
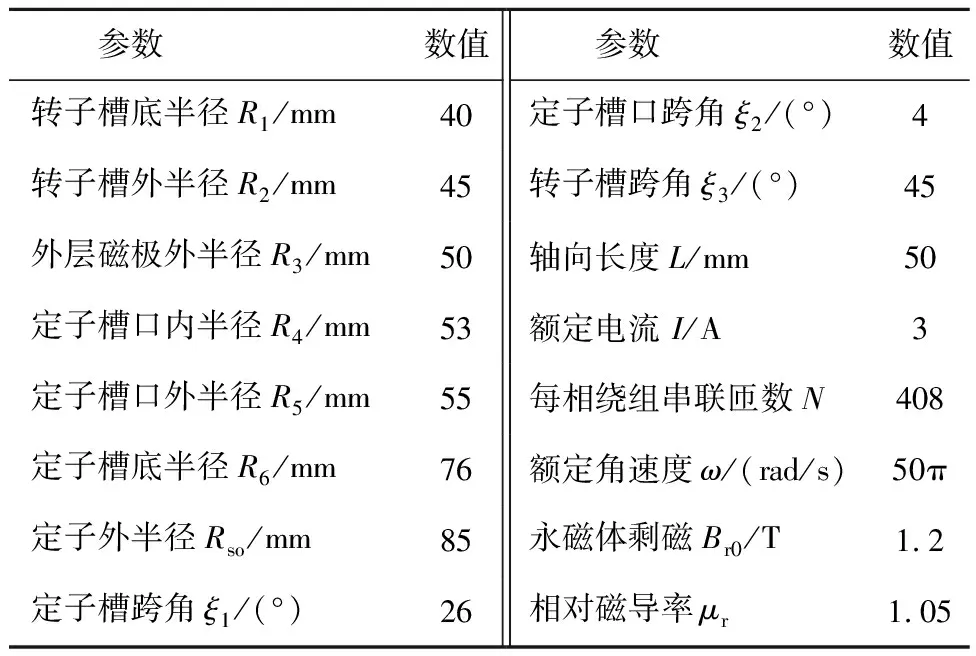
表1 新型双层半插入式交替极永磁电机的主要参数
图3比较了传统表面插入式永磁电机和新型双层半插入交替极永磁电机的气隙磁密波形和主要谐波分量。图4比较了这两种电机的空载感应电动势的波形和主要谐波分量。图5比较了这两种电机的电磁转矩波形。

图4 两种电机的空载感应电动势波形Fig.4 No-load back-EMF waveforms of two machines
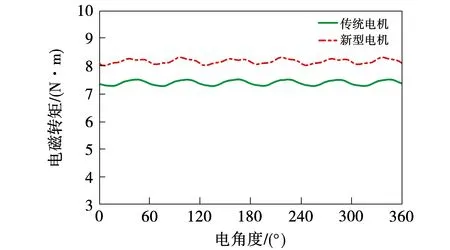
图5 两种电机的电磁转矩波形Fig.5 Electromagnetic torque waveforms of two machines
表2比较了这两种电机的电磁性能。可以看出,两种电机气隙磁密和感应电动势所含的偶次谐波幅值较小,奇次谐波幅值较大。新型电机虽然气隙磁密和感应电动势的谐波含量较高,但气隙磁密基波幅值和感应电动势基波幅值都较大。由于内层交替极磁极具有不对称性,新型电机的径向气隙磁密波形和感应电动势波形中都含有较高的3次谐波。在永磁体用量相同的情况下,与传统表面插入式电机相比,新型电机虽然转矩脉动略微增加,但是平均电磁转矩有明显的提升,提高了10.4%。
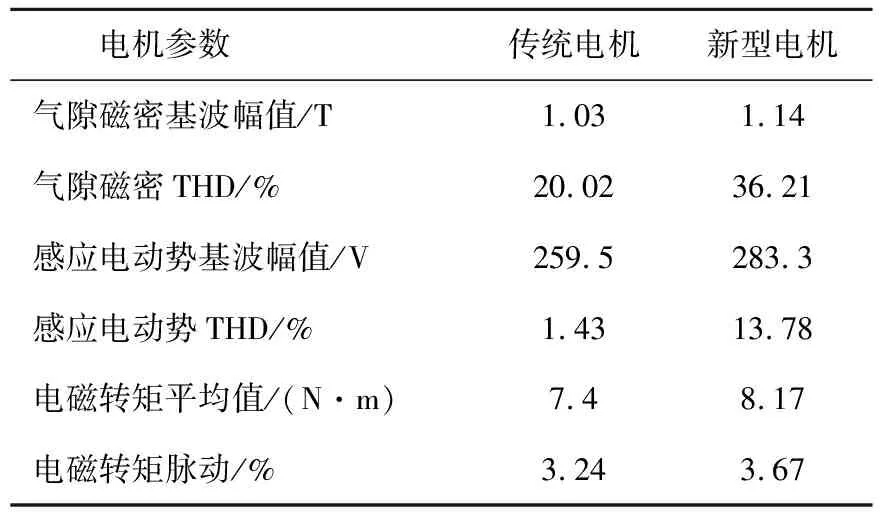
表2 两种电机的电磁性能比较
利用解析法和有限元法,计算得到新型电机的电磁性能,结果如图6所示。其中,感应电动势和电磁转矩的解析法结果略大于有限元结果,主要原因是计算各子域矢量磁位的直流分量和谐波系数时,由于受计算机硬件和软件限制,所取矩阵方程的阶数有限。但两种方法获得的波形总体一致性较好,验证了解析模型的正确性。
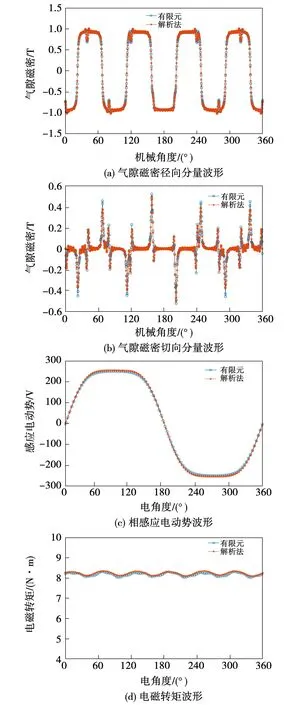
图6 气隙磁密、反电动势和电磁转矩波形有限元验证Fig.6 Finite element verification of air gap flux density, back-EMF and electromagnetic torque waveforms
5 结 论
本文提出了一种新型双层插入式交替极永磁电机模型,在内层为交替极磁极的基础上,外层增加了表贴式永磁体。使用二维子域模型法,对其进行解析建模,推导获得了各子域内的矢量磁位和谐波系数。以8极9槽新型电机为例,计算得到电机的气隙磁密、空载感应电动势和电磁转矩。结果表明,在永磁用量相同的前提下,与传统的表面插入式电机相比,提出的双层半插入交替极永磁电机虽然转矩脉动略微增加,但是平均电磁转矩显著提高。最后通过有限元法验证了解析模型的正确性。

