MW级双并列转子低速永磁直驱电机设计方法与性能分析

陶大军, 陈阳, 李凌霄, 戈宝军

(哈尔滨理工大学 大型电机电气与传热技术国家地方联合工程研究中心, 黑龙江 哈尔滨 150080)

0 引 言

二辊轧机、双螺杆泵等并行对驱机械设备在金属、医药等制造领域应用广泛。并行对驱机械设备的传统驱动方式是采用同步齿轮或同步带实现同步运行[1-2]。以二辊轧机为例,传统的驱动方式是用驱动电机通过同步齿轮装置将传动力分成2个,经过联轴器送到二辊轧机的2个辊轴上[3]。这种驱动方式由于采用了同步齿轮装置带来了机械、润滑等方面的问题,导致设备存在体积庞大、维护困难、效率不高、主从动轴同步性差、振动噪声大等问题。

针对以上问题,第一种解决方法是采用磁力齿轮代替机械齿轮[4],但对于大转矩直驱设备,磁力耦合可能会失效,此方法无法从根本上解决问题。第二种解决方法是使用两台电机分别驱动二辊轧机的2个辊轴,但是当电机并列放置时,由于双并列辊轴之间有着严格的距离限制,因此电机必须设计成细长型。而细长型电机在大转矩运行时,转子强度难以得到保证[5];同时,细长型电机还会带来线圈制造困难、下线难度大等问题;此外,利用两台电机驱动也增加了机械密封数量,使整个驱动系统的密封难度增大。

综上分析,本文提出了一种新型双并列转子永磁直驱电机(dual-parallel rotor permanent magnet direct-driven motor,DR-PMDM)。DR-PMDM由2个并列的转子和1个定子组成,定子可以看成是由2个切割掉部分定子的定子拼接而成,2个转子直接套装在二辊轧机的2个辊轴上用以驱动。电机与设备之间不需要使用同步齿轮,解决了由同步齿轮引起的一系列问题,且取消了联轴器,大大提高了整个传动系统的效率。

双转子永磁电机相比于传统电机,结构更紧凑,能够有效提高电机的功率密度、效率等[6]。双转子电机目前主要有同心式双转子电机、轴向磁通双转子电机、轴向并列转子电机等。国内外学者对这些电机的参数计算、优化设计[7-8]、模型建立[9-10]、分析方法[11-13]等问题进行了大量的研究,都取得了一定的成果。

对于双并列转子电机的研究,国内外仍处于起步阶段。沈阳工业大学的戴思锐、张炳义等设计了一台6 kW、4 500 r/min的定子连体双转子同步并行直驱永磁电机[14]。哈尔滨理工大学的陶大军、陈阳等对双并列永磁直驱电机转子的不平衡电磁力进行了研究,并提出5种优化方法实现了对不平衡电磁力的抑制[15]。浙江大学的黄家楠、章玮对此类电机的稳态特性进行了分析,建立了电机的统一电压方程[16]。双并列转子永磁电机设计方面的文献较少,耦合区的设计确定和选取原则是影响该类电机的关键环节之一,因此,研究此类电机的电磁设计方法具有理论意义和工程价值。

1 DR-PMDM基本结构

DR-PMDM是由1个定子和2个并列的永磁转子构成,如图1所示。其中,定子可以看成由2个完全相同的传统结构电机定子各自切割掉部分定子后拼接而成,拼接后的定子沿中心线呈镜像对称;2个转子均采用表贴式永磁转子结构。为了便于分析,本文把2个转子之间沿单侧圆周无绕组分布的区域定义为耦合区,见图1方框部分,图2为其放大图。耦合区所占的圆心角定义为耦合角α,°。耦合区中沿单侧圆周被切割掉的定子部分区域定义为占空区,所对应的圆心角称为占空角β,°。2个永磁转子之间的最小距离称为耦合间距d,mm。上述结构参数是双并列转子电机拼合区设计的关键,也是直接影响双并列转子电机定子磁路的关键。

图1 DR-PMDM基本结构Fig.1 Structure of DR-PMDM

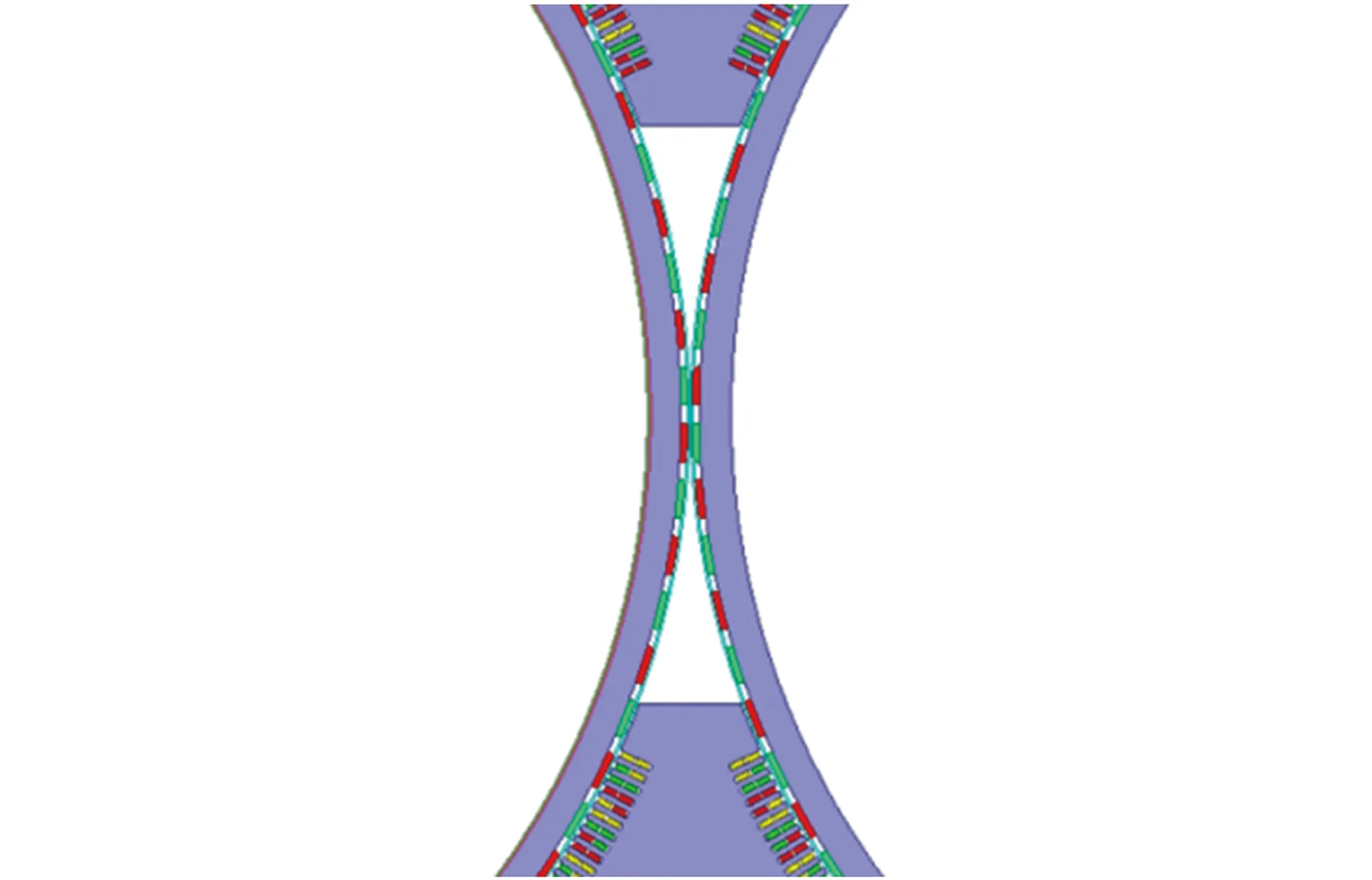
图2 耦合区示意图Fig.2 Coupling area of DR-PMDM

DR-PMDM的左右2个转子铁心上均匀分布永磁体,永磁体沿圆周方向N极、S极交替排列。与磁力齿轮相似,沿中心线镜像对称位置的永磁体极性相反,如图2所示。左右侧绕组都是非完整圆周分布,分别以逆时针和顺时针嵌放在定子槽内,沿中心线镜像对称位置的定子槽内绕组电流的流向完全相同,两套绕组采用并联方式。当两套绕组通以三相对称电流时,左右2个电机分别形成2个反向旋转的磁场,与各自的转子相互作用,产生一对反向旋转的电磁转矩,2个转子同步旋转。

2 DR-PMDM耦合区磁路分析

依据DR-PMDM的磁路特点,把其磁路分为耦合区和非耦合区两部分。非耦合区部分的磁路与传统永磁同步电机磁路结构相同,故本文仅对耦合区部分磁路分布进行研究。

DR-PMDM耦合区磁路示意图如图3所示,其中:PL1、PL2、PL3为左侧转子永磁体;PR1、PR2、PR3为右侧转子永磁体,以PL2为例,共有4条磁路。1)磁路1:永磁体PL2→气隙→定子铁心→转子间气隙→永磁体PL1→左侧转子铁心→永磁体PL2;2)磁路2:永磁体PL2→气隙→定子铁心→气隙→永磁体PR2→右侧转子铁心→永磁体PR1→转子间气隙→永磁体PL1→左侧转子铁心→永磁体PL2;3)磁路3:永磁体PL2→气隙→定子铁心→气隙→永磁体PL3→左侧转子铁心→永磁体PL2;4)磁路4:永磁体PL2→气隙→定子铁心→气隙→永磁体PR2→右侧转子铁心→永磁体PR3→气隙→定子铁心→气隙→永磁体PL3→左侧转子铁心→永磁体PL2。根据以上分析,即可建立DR-PMDM的等效磁路,如图4所示。

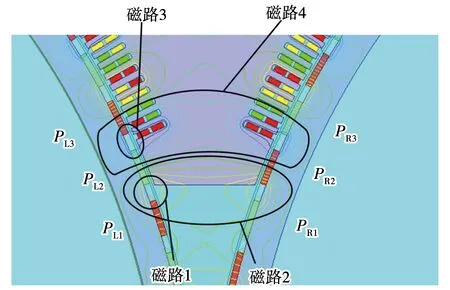
图3 DR-PMDM的磁路示意图Fig.3 Magnetic circuit of DR-PMDM

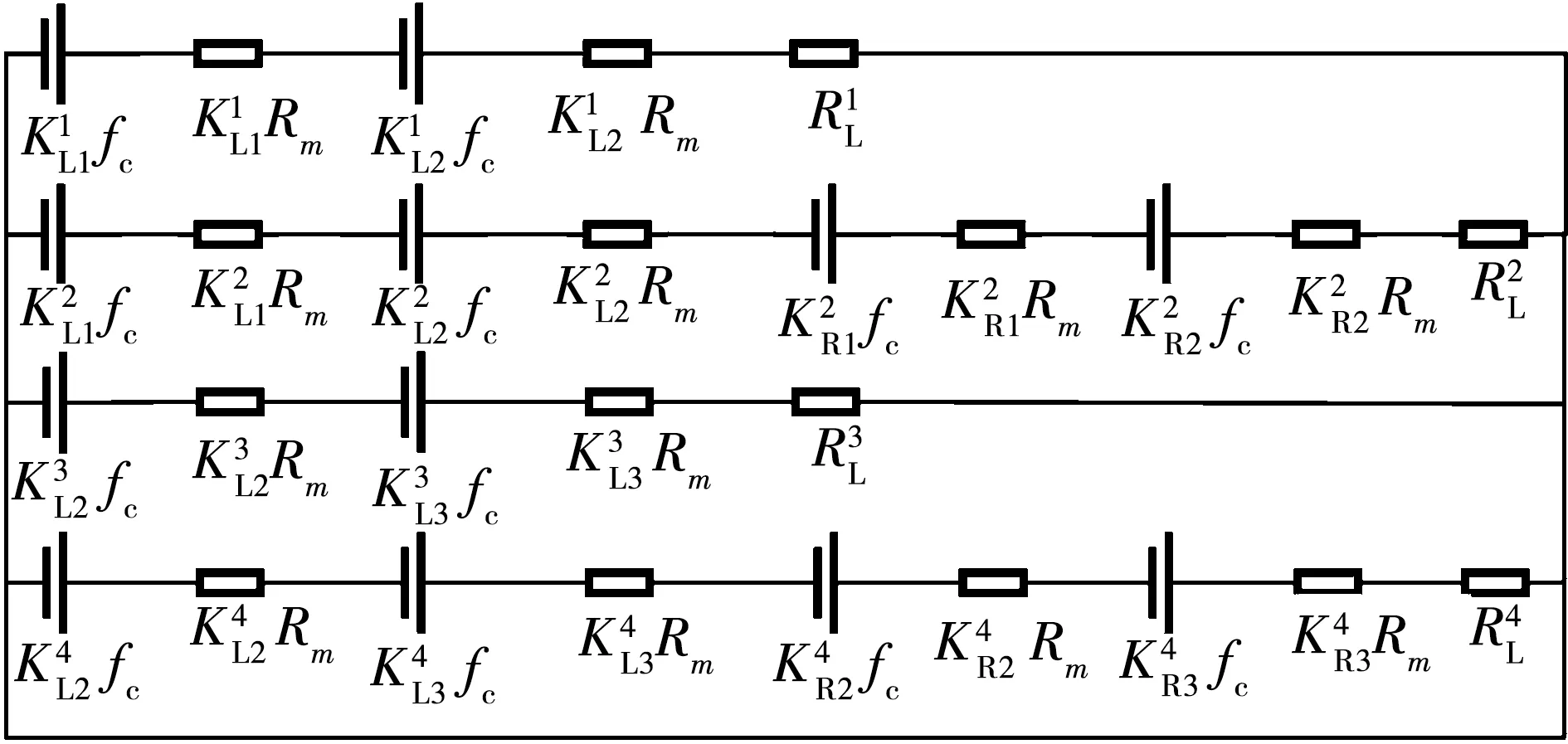
图4 DR-PMDM耦合区的等效磁路Fig.4 Equivalent magnetic circuit of coupling area

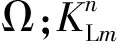
磁路方程为

KmFm=KmRmΦm+RLmΦm。

(1)

式中:Km为永磁体磁路系数比例系数矩阵;Fm为永磁体磁动势矩阵;Rm为永磁体内磁阻矩阵;RL为磁路磁阻矩阵;Φm为磁通矩阵。其中:

Km=

(2)

(3)

(4)

(5)

(6)

同时,永磁体的比例系数满足

(7)

3 耦合角的确定方法

3.1 基于模块组合式定子分块规则

低速大功率电机的体积相对于常速或高速电机大很多,过大的体积会给电机的制造、装配、运输等带来困难。对于本文研究的DR-PMDM,庞大的定子铁心非常适宜采用模块组合式定子。根据模块组合式定子分块规则[17],对于一个定子槽数为Q1、极对数为p的电机,可以分成gcd(Q1,p)个槽数为Q0、极对数为p0的单元电机,表达式为:

(8)

(9)

其中gcd(Q1,p)为Q1、p的最大公约数。

考虑到拼合后形成的DR-PMDM应包含成对的磁极,且为单元电机的倍数,耦合角α需满足:

(10)

式中:a为并联支路数;k为正整数。

3.2 基于冲片几何结构

为了避免靠近耦合区的左右2个定子槽重叠,从冲片的几何角度出发,耦合区附近应具有足够的轭部高度尺寸。耦合角α应满足的表达式为

(11)

式中:Dsi为单边电机定子内径,mm;δ为定、转子间气隙长度,mm;h为定子槽深,mm;hj为定子轭部高度,mm。

定子槽示意图如图5所示,各个参数之间满足:

图5 定子槽示意图Fig.5 Slots of stator

h=kbb1;

(12)

hj=ktt1;

(13)

b1+t1=t;

(14)

b1=kbtt;

(15)

(16)

式中:b1为定子槽宽,mm;t1为定子齿宽,mm;kb常取3.5～5.5;kt常取一个极下齿宽的和;kbt常取0.45～0.62;t为定子齿距,mm。

并行对驱设备一般都有固定的中心距am,因此定子内径Dsi和耦合间距d还受到am的约束限制,即其需满足

am=Dsi+d-2δ。

(17)

将式(12)～式(17)代入式(11)可推导出耦合角α满足的表达式为

(18)

由于定、转子气隙δ与耦合间距d远远小于定子内径Dsi,可认为中心距am与Dsi近似相等,式(18)可简化为

(19)

综合式(10)和式(19),即可得到耦合角α的选取规则为

α=α1≥α0。

(20)

式中:α1为式(10)的计算值;α0为由式(19)计算确定α的最小值。

4 DR-PMDM的电磁设计

本文研究的DR-PMDM用于驱动二棍轧机,主要设计指标如表1所示。DR-PMDM可以看成2个传统永磁电机通过切割部分定子后拼接而成,因此可先通过对单边传统电机进行设计;然后再借助单元电机思想,对拼接后的电机绕组进行优化设计。

表1 DR-PMDM主要设计指标Table 1 Main index of DR-PMDM

4.1 单边传统电机设计

由于分数槽绕组能够大幅度削弱高次谐波[18],故本设计选择每极每相槽数q为1.5。经过计算,单边传统电机的槽数为405槽,极对数为45。并联支路数设计为1。由式(11)、式(19)、式(20)计算得到耦合角α为48°,即定子切割掉54个槽,对应转子上12极所占的机械角度。

由于定子被切割,单边传统电机的额定功率PN1和额定电压UN1为:

(21)

(22)

电机的主要尺寸公式为

(23)

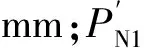
根据式(23)即可初步计算出单边传统电机的主要尺寸。经过分析计算,单边传统电机的主要参数如表2所示。所设计的单边传统电机的1/45模型如图6所示。

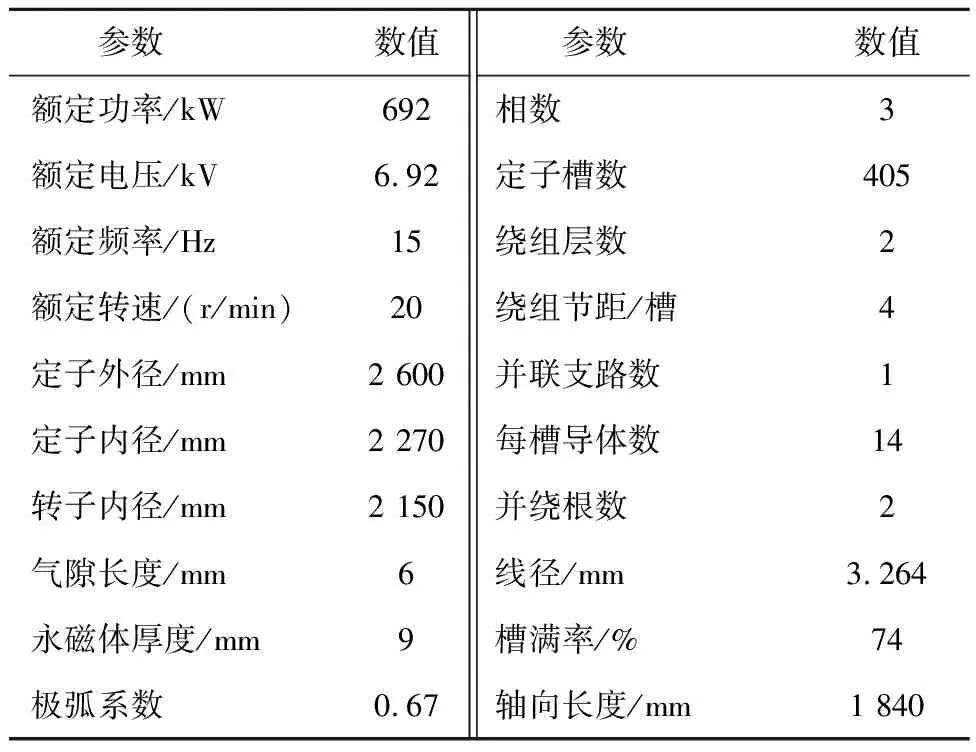
表2 单边传统电机主要参数Table 2 Main parameters of unilateral motor

图6 单边传统电机1/45模型Fig.6 1/45 of unilateral conventional motor

4.2 DR-pmdm绕组设计和定子端部设计

单边传统电机设计完成后,需要将其定子切割并重组。由于采用双层绕组,导致结尾处绕组无处安放。第一种方法是将一侧结尾处绕组直接横跨到同一侧绕组的起始处,绕组端部会跨越耦合区;第二种方法是基于定子分块原则,每一块定子为独立模块,采用大跨距线圈反向嵌放。本文采用第二种方法,ABC三相绕组排布如图7所示,L表示左侧绕组,R表示右侧绕组。DR-PMDM左右两侧绕组排布完全相同,沿中心线镜像对称。将左侧电机出线端与右侧电机出线端一一对应连接,采用并联方式,最终引出3个端子,由一台变频器供电驱动。

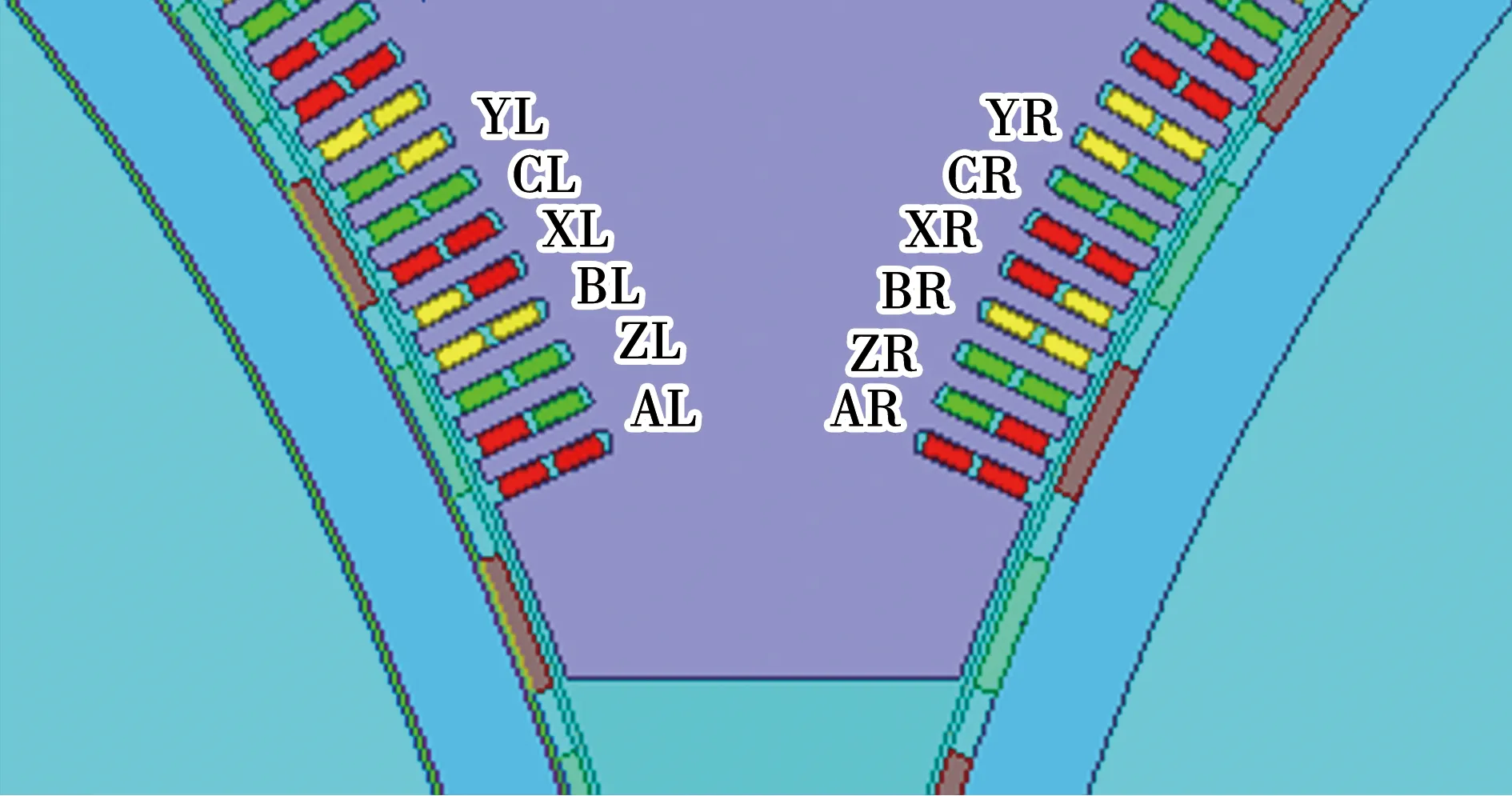
图7 电机绕组排布Fig.7 Arrangement of windings

定子拼合区的端部长度由耦合角α和占空角β决定。当耦合角α确定后,根据靠近端部绕组的磁场分布,合理选择占空角β,占空角β越大,端部长度越小。经过大量仿真计算,本文初选占空角β为36°。

5 仿真验证与分析

5.1 单边传统电机性能分析

单边传统电机空载运行时,磁力线分布和磁密分布如图8所示。由图可知,磁力线走势合理,磁密分布均匀,最大磁密出现在定子齿部,为1.40 T左右。空载气隙磁密和反电动势如图9、图10所示。由图可知,气隙磁密波形近似正弦,幅值最大值为0.74 T;空载反电动势有效值为3.9 kV,与额定相电压4 kV近似相等。

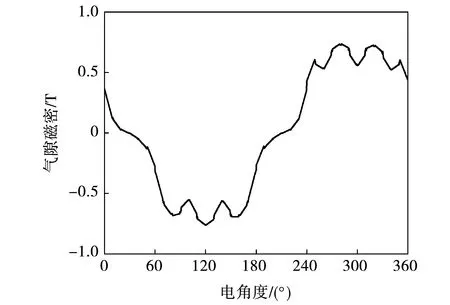
图9 单边传统电机气隙磁密Fig.9 Air gap magnetic density of unilateral motor

图10 单边传统电机空载反电势Fig.10 No load back EMF of unilateral motor

单边传统电机负载运行时,根据功率和转速解析计算得到的额定电磁转矩为330 kN·m。图11为所设计得到的单边传统电机电磁转矩,平均值为331 kN·m,转矩脉动为4.5%,达到设计指标。

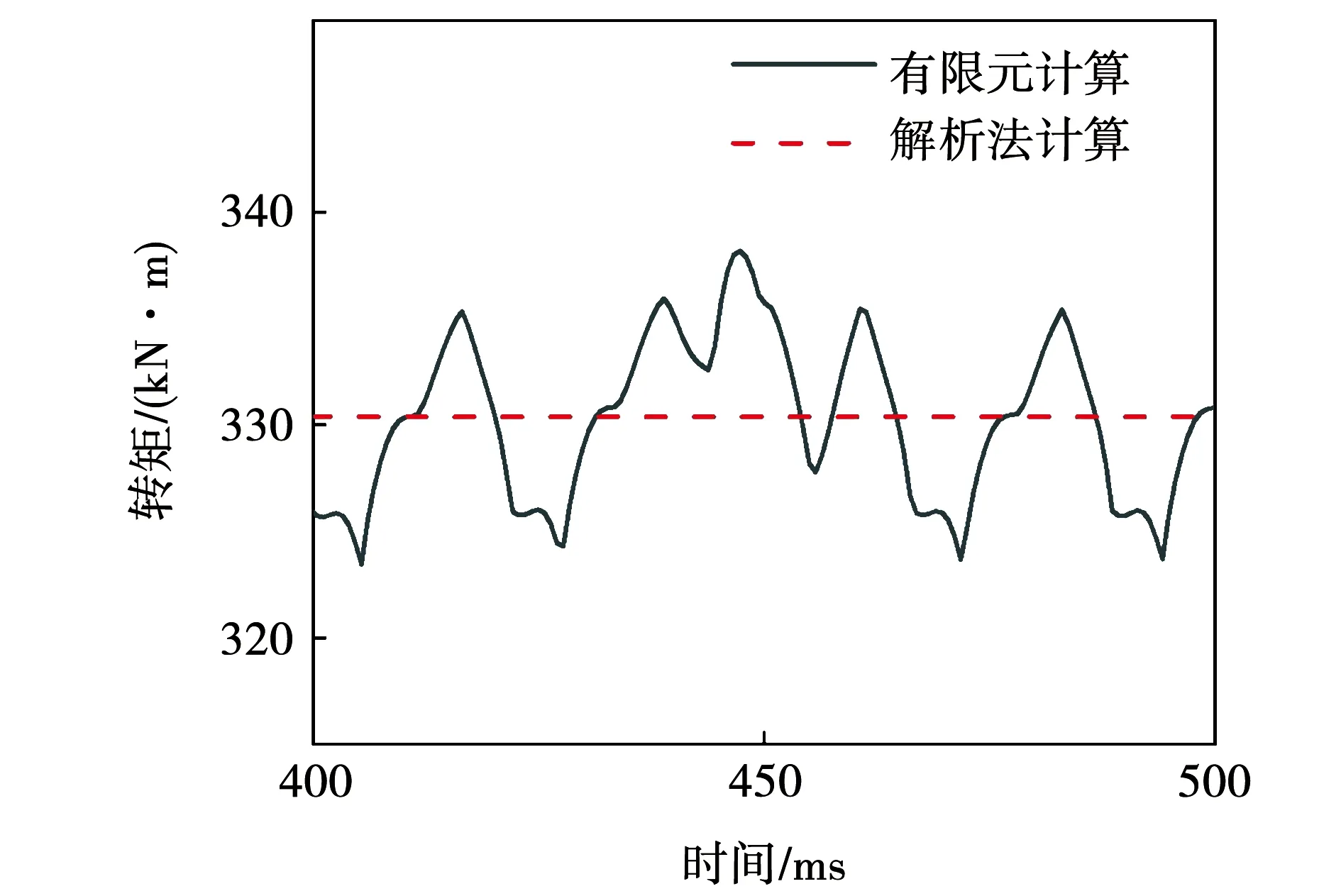
图11 单边传统电机电磁转矩Fig.11 Electromagnetic torque of unilateral motor

5.2 DR-PMDM性能分析

DR-PMDM存在耦合区,永磁体相互作用,会使耦合区内磁场发生改变。图12为DR-PMDM的单边气隙磁密,Br为径向磁密,Bt为切向磁密。由图12可知,径向磁密在耦合区内先减小后增大,这是因为2个转子的距离沿圆周先减小后增大,使磁路磁阻先减小后增大导致的。通过4.1节分析,切割掉的极数为12极,但图12中磁密分布不均匀部分的波峰波谷数量为10,这是由于占空区以外的耦合区处磁导与传统电机基本相同所导致的,即切割掉的占空区磁极数为10,占空区以外的耦合区内磁极数为2。切向磁密分布可认为近似均匀。

图13为DR-PMDM的空载反电动势,AL、BL、CL为左侧电机三相绕组,AR、BR、CR为右侧电机三相绕组。由图13可知,左右两侧电机的反电动势波形几乎完全重合,各相有效值为3.37 kV。由式(22)计算得到的值为3.38 kV,二者不完全相等,原因是耦合区边缘处存在边缘效应,但其影响基本可以忽略。

图13 DR-PMDM空载反电动势Fig.13 No load back EMF of DR-PMDM

图14为DR-PM DM两个转子的电磁转矩。分析该图可以发现,左侧转子输出电磁转矩的平均值为286.92 kN·m,右侧转子为-286.47 kN·m。二者旋转方向相反,大小基本相同,相差仅为0.45 kN·m,满足工程精度要求。电机的额定电流如图15所示,由图15可知,DR-PMDM的左右侧绕组对应相的电流基本相同。其中,A相、B相、C相电流的有效值分别为61、66、63 A,三相电流幅值不完全相等的主要原因是绕组采用了大跨距线圈反向嵌放的连接方式,使每相绕组的电感电阻稍有差异。

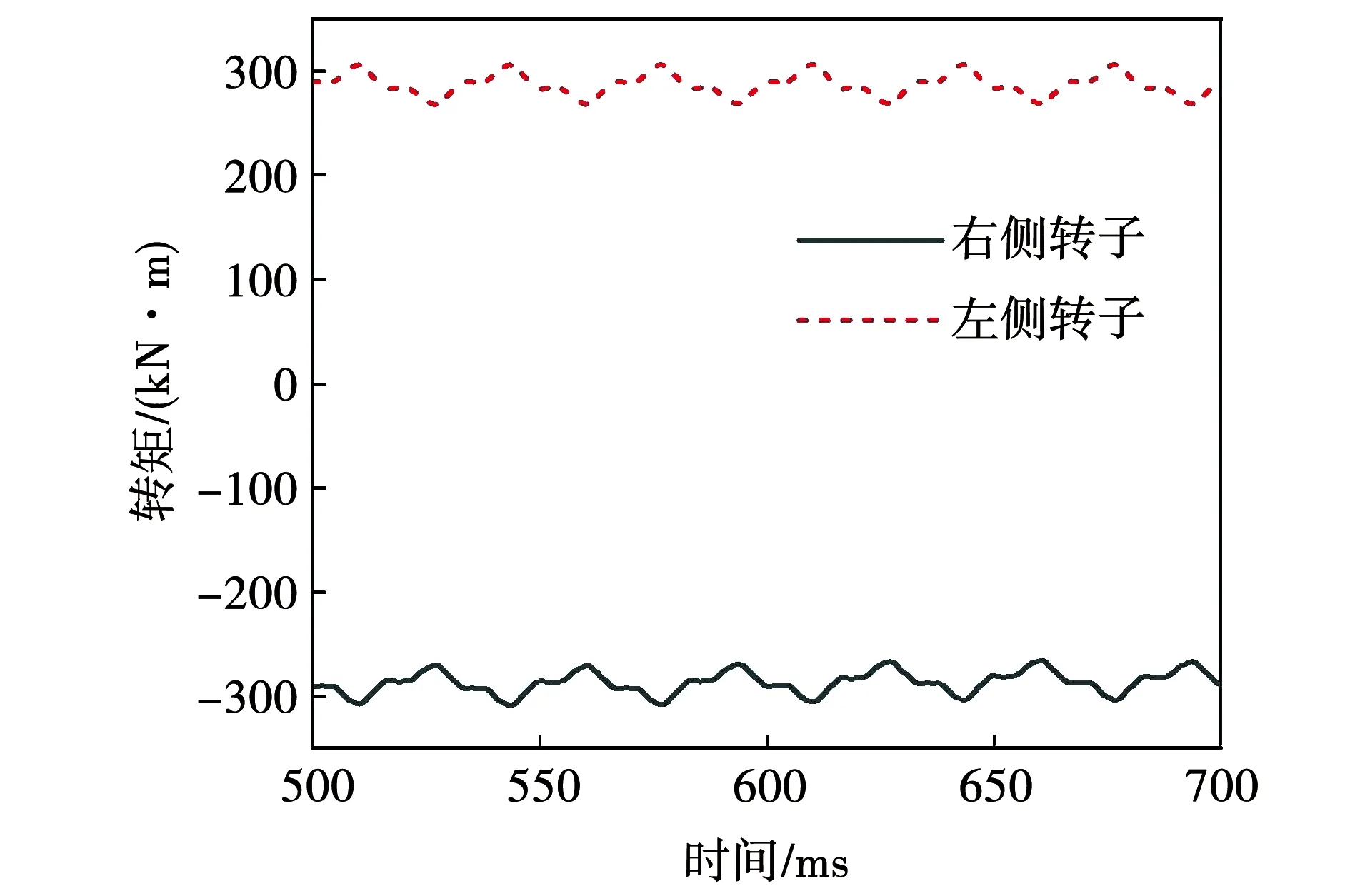
图14 DR-PMDM的电磁转矩Fig.14 Electromagnetic torque of DR-PMDM

图15 DR-PMDM的电流Fig.15 Current of DR-PMDM

图16为DR-PMDM稳态运行时耦合区的磁力线分布和磁通密度云图。由图16可知,磁力线走势与上文耦合区磁路分析相同,左右两侧电机定子拼合处存在磁力线交链的情况,定子端部存在少量漏磁,占空区内永磁体存在相互作用。磁密分布合理,最大磁密处出现在定子齿部,为1.54 T。

电机效率表达式为

(24)

式中:P2为输出功率;ΣP为电机损耗总和,包括定转子铁心的铁耗、左右侧绕组总铜耗以及机械损耗和杂散损耗。

经过有限元计算,输出功率为1 200 kW,总铁耗4.55 kW,总铜耗98.13 kW,机械损耗和杂散损耗估计为输出功率的1%。经过计算,本文所研究的DR-PMDM效率约为91.28%。同时,根据电压电流相位计算电机的功率因数为0.99。

6 占空角对转矩脉动和径向电磁力的影响

由于定子的部分缺失导致DR-PMDM的转矩脉动过大,且两侧转子所受的电磁力不平衡。耦合间距d受辊轴之间距离约束且耦合角α已经确定,因此,本节仅探讨占空角β对转矩脉动和转子所受径向电磁力的影响。

图17为转矩脉动随占空角β的变化情况。由图17可知,随着占空角的增加,转矩脉动整体呈下降趋势。当占空角为12°、28°、44°时,转矩脉动出现极小值。此时,耦合角α和占空角β满足式(25),即从转矩脉动角度出发,占空角选取应满足的基本原则是

(25)

式中k1为自然数。

DR-PMDM转子所受的电磁力较为复杂。除了由于缺失部分定子铁心和绕组引起的不平衡电磁力外,耦合区内的2个转子永磁体之间存在作用力,且定子拼接处的端部存在类似于直线电机的磁阻力。图18为单侧转子所受电磁力的合力随占空角β的变化情况。

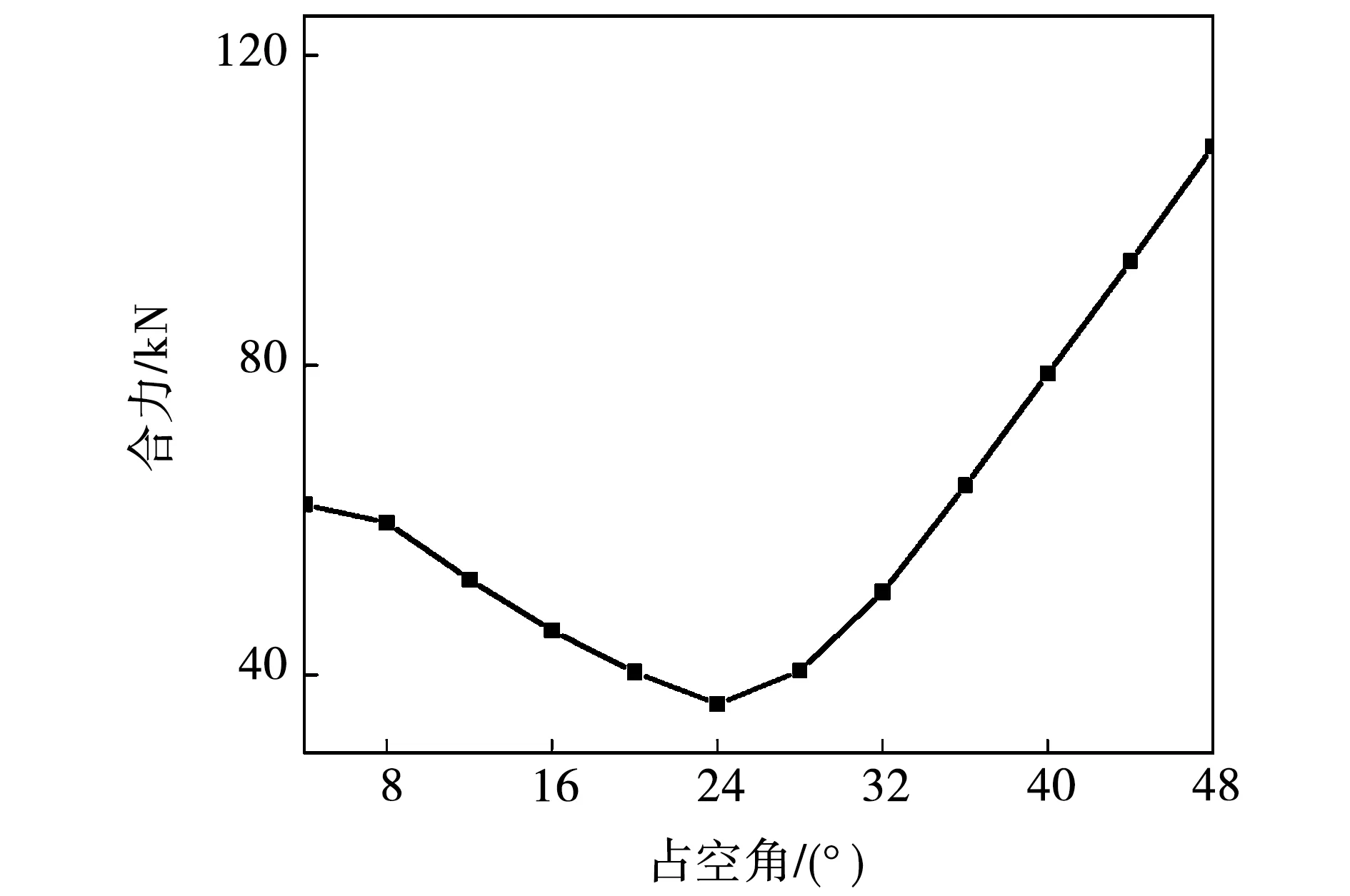
图18 不同占空角下的转子所受径向电磁力Fig.18 Radial electromagnetic force on the rotor under different duty angle

由图18可知,随着占空角的增加,转子所受的径向电磁力先减小后增大,当占空角为24°时,合力最小。此时,2个转子永磁体之间作用力和定子铁心拼接处端部磁阻力能够抵消掉大部分由于单边电机定子缺失引起的不平衡电磁力。综合分析图17和图18,最终占空角选取为28°。

7 结 论

本文提出了一种双并列转子永磁直驱电机。阐述了电机的基本结构,定义了耦合区内耦合角、占空角和耦合间距;利用等效磁路法研究并分析了耦合区内的等效磁路;对一台1 200 kW的双并列转子电机进行了初步设计;通过数值仿真验证了设计方法的可行性和正确性。得到的主要结论如下:

1)当电机的极数、槽数确定以后,耦合角即可确定,从模块式定子分块规则和冲片的几何结构2个角度出发,给出了耦合角的确定方法。

2)设计双并列转子电机时,可先对单边传统电机进行设计,但要注意功率和电压的分配。

3)由于耦合区的存在,电机的气隙磁场在耦合区内发生改变;占空区以外的耦合区对耦合区磁场有显著影响,设计时应重点考虑。

4)转矩脉动随占空角的增大呈下降趋势,转矩脉动出现极小值时的占空角与耦合角存在一般规律。转子所受不平衡电磁力随占空角的增大先减小后增大,设计时应综合考虑占空角对二者的影响。