改进成分分析的差分隐私高维数据发布方法
褚治广 张 兴 张青云 李晓会 李万杰
(辽宁工业大学电子与信息工程学院 辽宁 锦州 121001)
0 引 言
目前,许多数据收集机构需要将所收集原始数据(例如医疗数据、金融数据等)发布出去,以便于数据分析、挖掘,能够从发布的数据中产生更为有效的决策支持。然而,发布的原始数据中涉及了大量的个人敏感信息,直接发布数据会致使个人隐私的严重泄露。因此,数据发布者需要通过特殊的保护技术处理隐私数据后将数据发布出去。
现阶段,主要的隐私保护数据发布技术大致上分为三类:1) 基于数据加密的发布技术。例如AES加密、RSA加密等。2) 基于限制条件的发布技术。根据原始数据特性,有选择性地发布含有敏感数据的数据,例如:k-匿名模型[1-3]、l-多样性模型[4]、t-近似模型[5]等。3) 基于数据失真的发布技术。使得隐私数据失真的同时,保持原始数据的某些特性。这样的技术主要有:随机扰动[6-8]、凝聚[9-10]、交换技术[11]、注入噪声[12-13]等。
作为基于数据失真的差分隐私保护技术,已成为隐私保护重点研究方向之一。现阶段,对于数据发布的研究主要聚焦于一维或低维数据。然而,这些数据发布方法均不适用于高维数据的发布,无法解决在处理高维数据发布时,随着维度和维度值域的增加,形成的发布空间以指数型增长,遭遇“维度灾难”的问题。因此,如何为数据研究者提供大量有效信息的同时,利用差分隐私技术保证原始高维数据的隐私安全变得极具挑战。
基于此,本文提出一种基于改进成分分析的差分隐私高维数据发布方法(ICAHDP),使得数据隐私信息不被泄露的同时,发布的数据更好地接近原始数据。本文的主要贡献总结如下:
1) 提出一种满足差分隐私的主成分分析优化的高维数据发布方法(ICAHDP),减少了处理数据的时间和空间开销,提高发布数据的可用性。正式证明ICAHDP满足差分隐私。
2) 在ICAHDP中,为了降低成分分析方法在降维过程中的时间和空间成本,提出一种优化主成分分析(PCAO)的方法。利用属性重要性对属性进行过滤,压缩数据空间,从而优化了高维数据降维时占用空间大、处理时间长的问题。此外,为了解决优化算法中主成分数量(k)的选取问题,引入基于互信息的评价机制对原始数据和已发布数据进行评价,确定最优k。
3) 考虑了高维数据中多敏感属性的存在,而传统的隐私预算分配方法不能满足个性化的隐私保护。将敏感偏好度和最优匹配理论相结合,设计了敏感属性层次保护策略,使高维数据在不同隐私要求下能够发布。
4) 对不同的真实数据集进行广泛的实验。实验结果表明,与PrivBayes[14]和JTree[15]等方法相比,ICAHDP不仅保证了已发布数据集的隐私性,而且显著提高了数据的准确性和实用性。
1 相关工作
目前,对于高维数据发布方法的研究,已有少量研究成果[14-20],然而这些方法都存在着一些问题:
文献[14,16-17]是基于概率图模型的高维数据发布方法。其中,PriView[16]算法构建k个属性对的边缘分布,然后估计出高维数据的联合分布。该方法假设数据中的所有属性对相互独立,均等地处理属性对,然而在实际的高维数据集中,属性之间大都存在相关性。Zhang等[14]提出的PrivBayes算法使用指数机制满足差分隐私条件下,结合贝叶斯网络近似属性之间的联合分布,生成高维数据集。然而利用指数机制挑选属性对时,受到候选空间的大小的制约。候选空间越大,指数机制挑选属性对的精度越低。Chen等[17]在上述方法的基础上,提出了JTree算法。该算法采用稀疏向量技术寻找属性对的关联性,通过联合树构造属性关系图所确定的边缘分布估计相应的联合分布。然而稀疏向量技术不满足差分隐私[15],致使JTree算法不能满足差分隐私的要求。文献[18]是基于投影技术的高维数据发布方法。PrivPfC[18]算法结合投影直方图和卡方关联测试达到高维数据发布的目的,然而,投影直方图并没有考虑到属性之间的相关性,导致发布精度较低。Hb[19]算法结合直方图技术和层次树发布高维数据,但是当数据维度较高时,该方法发布的数据实用性越来越低。Jiang等[20]提出一种基于主成分分析的差分隐私数据发布方法,该方法首先构建噪声协方差矩阵,然后通过还原加噪后的投影矩阵来发布数据。然而在构建噪声协方差矩阵时浪费了一部分隐私预算,而且该方法在处理属性维度较大的数据时,处理时间无法满足实际要求。
基于以上分析,本文提出一种改进的成分分析优化的差分隐私高维数据发布方法ICAHDP。该方法通过引入属性重要度和互信息评价机制对PCA进行优化,利用优化后的主成分分析法(PCAO)对数据进行降维。在数据降维的过程中,设计了个性化的拉普拉斯机制,既保证了ICAHDP满足差分隐私的要求,又使隐私保护更加灵活。理论分析表明,所提的ICAHDP算法满足ε-差分隐私。实验表明,与现有的研究工作相比,ICAHDP算法产生的数据集的数据效用性均优于PrivBayes、DPPro和JTree等算法。
2 相关定义
2.1 差分隐私
差分隐私保护技术通过向原始数据集的转换或其统计结果添加噪声来达到隐私保护的目的。该方法确保了在任一数据集中更改一条记录的操作而不影响查询的输出结果。此外,该模型可以抵御攻击者掌握了除某一记录外的所有信息的背景知识攻击。
定义1差分隐私[21]。给定两个数据集D和D′,二者完全相同或者至多相差一条记录,给定随机算法A,Range(A)表示A的值域,S为Range(A)的子集。如果A满足式(1),则算法A满足ε-差分隐私。
Pr[A(D)∈S]≤eε×Pr[A(D′)∈S]
(1)
式中:概率Pr[·]表示算法的概率,由算法A决定;ε为隐私预算,表示算法A的隐私保护程度,ε的值越小,A的隐私保护程度越高。
实现差分隐私保护常介入两种噪声机制,分别是拉普拉斯机制和指数机制[22]。本文主要采用Laplace噪声机制。
定义2Laplace机制[22]。给定数据集D,对于任一查询函数f:D→Rd,其敏感度为Δf,则随机算法A(D)=f(D)+Y提供ε-差分隐私保护。其中,Y~Lap(Δf/ε)为随机噪声,表示Y是服从尺度参数为Δf/ε的Laplace噪声分布。
Laplace机制[23]通过将服从Laplace分布的噪声介入准确的查询统计结果来达到ε-差分隐私保护的目的。设Laplace分布Lap(b)位置参数为0的概率密度函数为p(x),其表示形式为:
(2)
2.2 信息熵与互信息
1948年,Shannon将热力学的熵引入信息论,提出了“信息熵”的概念,解决了信息度量的问题。信息熵表示事件中包含信息量的平均量。信息熵越高,表示包含的信息量越大;反之,信息熵越小,表示包含的信息量越少[24]。信息熵的定义为:
定义3设X是一个离散型随机变量,则X的信息熵为:
(3)
式中:p(x)表示x发生的概率。
互信息[25](Mutual Information)是2个或2个以上随机变量间相互依赖性的量度。它度量两个事件之间信息量的相关性。互信息的定义为:
(4)
式中:X和Y表示两个离散随机变量;p(x,y)表示X和Y的联合概率分布函数;p(x)和p(y)分别为X和Y的边缘概率分布函数。
由式(3)和式(4)推导可得互信息与信息熵之间的关系:
I(X,Y)=H(X)+H(Y)-H(X,Y)
(5)
2.3 主成分分析法
主成分分析法[26](PCA)是通过对多个原始随机变量组成的数据集X={x1,x2,…,xn}的协方差矩阵进行分解,重新组合转变为少数几个各维度间互不相关的变量Q={y1,y2,…,ym},m 在高维数据发布时,现有的大多数方法都会遭受维度“灾难”的问题,引入较大的噪声,导致发布的数据的可用性很低。因此,在高维数据发布中,设计出既能解决维度灾难带来数据可用性较低的问题又能满足数据隐私安全的发布方法是亟需迫切的。本文提出一种基于主成分分析优化的差分隐私高维数据发布保护方法,对高维数据进行降维优化及隐私保护,经该方法产生的发布数据满足:1) 具有较好的数据效用,利于数据挖掘、分析操作等;2) 满足差分隐私保护,为数据提供最优的隐私保护效果。 改进的成分分析优化的差分隐私高维数据发布方法的运行机制如图1所示。 图1 成分分析优化的差分隐私高维数据发布框架 基于主成分分析优化的差分隐私高维数据发布方法具体的步骤如下: 1) 首先确定属性重要度阈值,对原始数据中的属性进行筛选,将原始数据中的无用属性和缺失值较多的属性剔除。 2) 对经过属性筛选后的数据,利用主成分分析法对数据进行降维。对降维过程中,对产生的投影矩阵加入Laplace噪声,使得数据满足差分隐私。 3) 在满足差分隐私的前提下,对数据属性的敏感偏好进行分级,并结合最优匹配理论来分配隐私预算。将不同大小的噪声添加到数据集中不同敏感偏好的属性中,实现个性化的噪声添加方法,使发布的数据具有更好的可用性。 4) 在数据的降维过程中,进行多次的主成分个数k值的选取,通过互信息评价机制,计算原始数据与加噪数据的互信息,确定最优的k值,从而确定最佳的发布数据。 本文算法通过计算属性的信息熵,作为属性重要度衡量指标,利用属性重要度阈值,对属性进行筛选。 信息熵应用于衡量属性“重要”程度时,该属性的信息熵越大,表示该属性包含的信息量越多,则属性的“重要”程度越高;反之属性的信息熵越小,表示该属性包含的信息量越小,属性的“重要”程度越低。在数据降维时,尽可能保留属性重要度越高的属性,剔除重要度越低的属性。在衡量属性保留或者舍弃时,本文以属性重要度阈值Th作为界限。阈值的确定采用以下方案: 计算选择的属性在数据中所占的比重。计算式如式(6)所示。 (6) 通过计算数据集中各个属性的信息熵,按照重要度大小排列属性,以属性重要度阈值作为界限,属性的重要度大于阈值时,说明该属性包含的信息量多于阈值下的信息量,在数据降维时保留该属性;反之属性的信息熵小于阈值时,表示该属性包含的信息量少于阈值下的信息量,在数据降维时剔除该属性。 若数据集D经筛选属性后产生的数据集为Do,利用主成分分析法对其进行降维,降维过程如下: 计算样本的协方差矩阵: (7) 对协方差矩阵进行特征分解: Cov=UTCU (8) 式中:C表示Cov特征分解后的对角矩阵;U表示特征值所对应的特征向量构成的特征矩阵。 选取k个特征值所对应的k个特征向量组成矩阵Uk,将原始数据投影到矩阵Uk上,得到投影矩阵: (9) 在投影矩阵Z中添加Laplace噪声,得到噪声矩阵Zo。 还原得到原始数据矩阵的低阶近似矩阵: (10) 在投影矩阵上添加Laplace噪声,由于用户对自身数据的隐私需求不同,不同的属性的敏感程度不同,因此需要为不同的敏感属性添加不同的噪声量,提供不同的隐私保护程度。本文设计了个性化地添加噪声的策略。 定义4敏感属性偏好。敏感属性偏好表示用户对敏感属性数据的重视程度。即同意哪些属性被披露,禁止哪些属性被披露。 定义5敏感偏好度。为了便于在隐私保护过程中定量分析敏感属性的偏好,需要对敏感属性偏好进行量化,用于表示敏感属性的重要程度,称为敏感偏好度SP。设数据集D中存在n个敏感属性{P1,P2,…,Pn},敏感属性pi的数据不愿被披露程度权重作为pi的敏感偏好度spi。 由每一个敏感属性敏感偏好度spi组成DSP={sp1,sp2,…,spn}为D的敏感偏好度集合,其中spi为[0,1]区间中的一个数值。 敏感偏好度反映了数据拥有者要求对敏感属性数据进行保护的倾向程度,可以由数据拥有者的主观评价或敏感程度而确定。敏感偏好度越大,该敏感属性的隐私保护需求越高,反之,敏感偏好度越小,该敏感属性的隐私保护需求越低。 根据敏感属性敏感偏好度值spi,将敏感属性划分为m个等级,对应m个隐私保护强度。差分隐私保护强度与隐私预算有关,每个等级对应一个隐私预算,如表1所示。 表1 敏感属性等级与隐私预算对应表 定义6隐私造价。设Tij=Gi×εj是隐私预算为εj对于隐私保护强度Gi对应的敏感偏好等级的隐私造价。 定义7最优匹配。设有二部图(x,y),如果找到一组匹配数最大的方案,记为最大匹配。若|x|=|y|=匹配数时,该匹配方案为最优匹配(PM)。 定义8偏好隐私预算分配图。设能为发布数据提供最大数据效用的隐私预算,与每个敏感属性等级之间的连线形成的图为一个偏好隐私预算分配图PA。 本文设计的加噪方式类似于二部图的最优匹配。给定一组敏感属性对应的m个敏感等级,一组k个隐私预算的集合,将这组敏感属性等级以使发布的数据与原始数据的I(*)最大的方式匹配给这组隐私预算。最匹配的过程是先设置每个初始敏感属性的隐私损失Pli=0,计算Tij,用Tij-Pli表示敏感属性在Gi下的信息量损失,然后根据损失函数构造偏好隐私预算分配图PA,检查图中是否存在完美匹配。如果存在,匹配过程结束,得到一个最优匹配;否则存在受限隐私预算,把与受限隐私预算关联的敏感属性的Pli加一个单位,重复上述过程,直到存在完美匹配结束。加噪方法如算法1所示。 算法1加噪方法 输入:敏感属性{P1,P2,…,Pm},差分隐私预算εj。 输出:最优匹配PM。 1. 对于每一个Pi做以下操作: 2. 设置初始敏感属性的隐私损失Pli=0 3. 对于每一个隐私预算εj做以下操作: 4. 计算Tij 5. 偏好隐私预算分配图PA 6.IF存在完美匹配 7. 结束匹配 8. 获得最优匹配方案PM 9.Else 10. Pli+1 11. 返回第5步 12.End 主成分个数k的选取,在整个算法过程中阈值进行人为的选取是不切实际的,主成分分析k值的选择很大程度地影响着数据的安全性、可用性、处理数据花费时间。k值选择过小,导致较多的属性被剔除,还原后的噪声数据的可用性较低;k值选择过大,还原后的噪声数据更加接近原始数据,但是数据的安全性降低。因此,怎样选择最优的主成分个数k是PCA优化算法的挑战之一。 本文引进互信息的概念,通过计算不同主成分个数k值下的噪声数据与原始数据的互信息大小,利用均值法,将最接近均值的k值,作为发布数据安全性和实用性达到最优的主成分个数。 互信息越大,变量之间的相关性越强,数据实用性越强。用互信息去衡量加噪后的数据集更接近原始数据集的关系是可行的。 基于主成分分析优化的差分隐私高维数据发布算法如算法2所示。算法2对优化主成分分析的高维数据发布的实现进行了概述。利用属性重要度筛选属性、最优主成分个数k的确定方法对主成分分析法在差分隐私数据发布中的改进,很大程度地提升了数据的可用性和减少了数据处理的时间。 算法2ICAHDP 输入:原始数据集Sm×n,属性重要度阈值Th,差分隐私预算ε。 输出:发布数据集S″。 1.对每一个属性做以下操作: 2.计算属性ci的信息熵H(ci) 5.END IF 6.END 7.计算b11,bi21,…,bp1 9.得到向量B=[b11,b21,…,bp1]T 12.计算Cov=UTCU, 其中C=Λ=diag[λ1,λ2,…,λp] 13.选择U中最大的k个特征向量组成特征向量矩阵Up×k 14.k值的选取,根据互信息值确定 15.计算得到投影矩阵Zk×n 16.对投影矩阵Zk×n添加噪声 18.得到带有噪声的矩阵Z(noise) 19.计算e11,e21,…,ep1 20.得到向量E(noise)=[e11,e21,…,ep1]T 21.还原数据集S″ 22.S″=Up×k×Z(noise)+repmat(E(noise),1,n) 23.求出互信息I(Sm×n,S″),确定最优K值。 定理1所提出的ICAHDP算法满足ε-差分隐私保护。 证明由算法可知: 噪声矩阵为: 由Laplace机制即证: 因为特征向量矩阵Up×k中的任意两个特征向量互相正交,则有: 所以: 得证。 得出结论:ICAHDP算法满足ε-差分隐私保护。。 为了对ICAHDP算法的有效性进行验证,本节将采用具体的实验进行分析说明。 实验环境:Windows 10操作系统,Intel(R) Core(TM) i3-8100 CPU 3.6 GHz,16 GB内存。所涉及的算法和代码用Python实现。 实验数据:实验中采用UCI Adult、Diabetes 130-US hospitals for years 1999年-2008年 Data Set(Diabetes)和TIC三个数据集,三者均被广泛运用于数据发布。Adult是美国人口普查数据,记录了48 842条个人信息;Diabetes是1999年-2008年美国130家医院的糖尿病患者数据,记录了101 767条糖尿病患者信息;TIC是某保险公司的客户信息数据,记录了98 220条客户信息。数据集的数据类型、样本数及维度如表2所示。 表2 数据集描述 为了评估本文算法的性能,分别采用以上三种数据集,对ICAHDP、PrivBayes、JTree、DPPro算法、NoPrivacy(不加噪声)进行高维数据发布时,采用SVM分类算法度量数据的有效性。使用发布后的数据构建SVM分类模型,选择一个属性作为分类属性,其他属性作为特征,训练SVM分类器,并且做出预测。本文针对不同数据集选取不同的属性作为分类属性。为进一步评价算法的有效性,使用误分类率(Misclassification rate)作为数据可用性的衡量标准,来度量发布数据的SVM分类结果的准确性。 首先在Adult、Diabetes、TIC数据集上,通过5种算法生成添加噪声后的发布数据集,将70%的生成数据作为训练集,30%的数据作为测试集,然后在发布数据集上构建SVM分类器。基于5种算法为随机算法,为了减少只进行一次实验产生不可避免的误差,因此在三种数据集上分别进行了10次实验,计算实验结果的平均值作为最终的实验结果。 在Adult数据集上,分别以是否拥有大学学历、是否结婚作为分类属性做出预测。在Diabetes数据集上,分别以是否为男性、是否再次入住医院作为分类属性做出预测。在TIC数据集上,分别以否拥有房子、是否结婚作为分类属性做出预测。 图2、图3及图4分别展示了5种算法在Adults、Diabetes、TIC数据集上的误分类结果。 (a) Adult, education (a) TIC, house 可以观察到,几乎在所有情况下,ICAHDP始终在4个数据集上表现出比其他解决方案更好的性能。这是因为ICAHDP可以实质上提取数据集中属性的主要成分。将高维数据映射到低维空间,通过将隐私预算分配给低维数据,可以将噪声添加到更加敏感的属性中。对于其他属性,将会减少噪声干扰,使数据的实用性得到极大的提高,最终产生发布的数据比其他解决方案具有更好的实用性。 针对高维数据发布问题,首先,阐述了隐私保护的研究背景和意义;其次,分析现有的高维数据发布方法的优点与不足;最后,提出一种改进成分分析的差分隐私高维数据发布方法ICAHDP。理论分析表明,ICAHDP不但对高维数据发布具有较好的优化而且满足差分隐私。实验结果表明,ICAHDP算法与现有的同类算法相比,生成的数据集具有较好的效用性。尽管ICAHDP针对高维数据隐私保护有较好的效果,但是该方法也存在着一些局限性,例如其研究对象只能针对数值型静态高维数据。因此,未来将针对动态的、非数值型高维数据发布提出相应的差分隐私保护方法。3 改进的高维数据发布方法
3.1 问题描述
3.2 高维数据发布机制
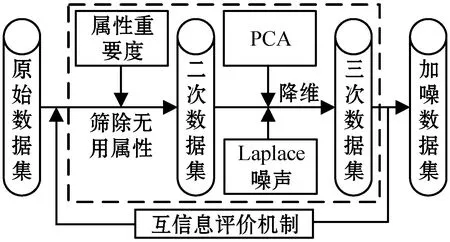
3.3 筛选属性
3.4 数据降维加噪
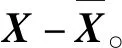
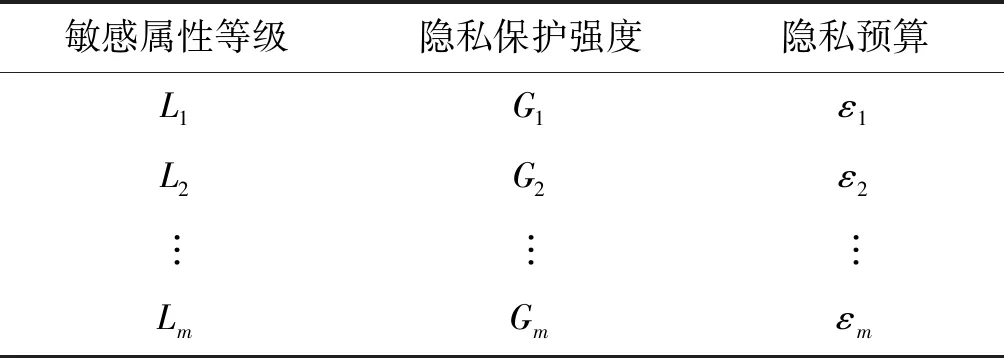
3.5 互信息评价机制
3.6 算法描述
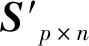
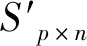
3.7 算法隐私保护效果分析
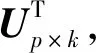
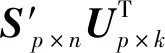
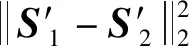
4 实验评价
4.1 实验设置
4.2 实验结果分析
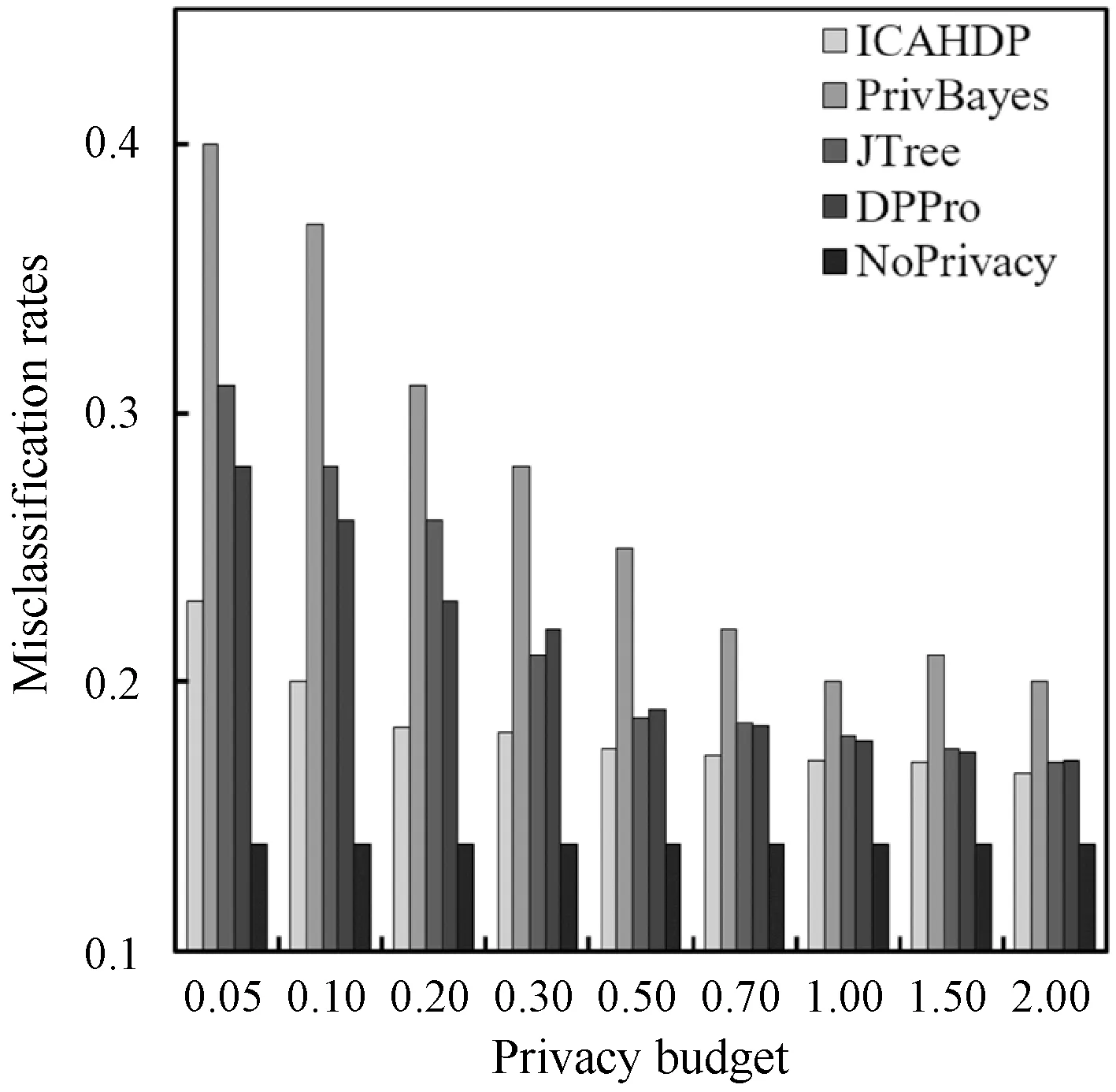
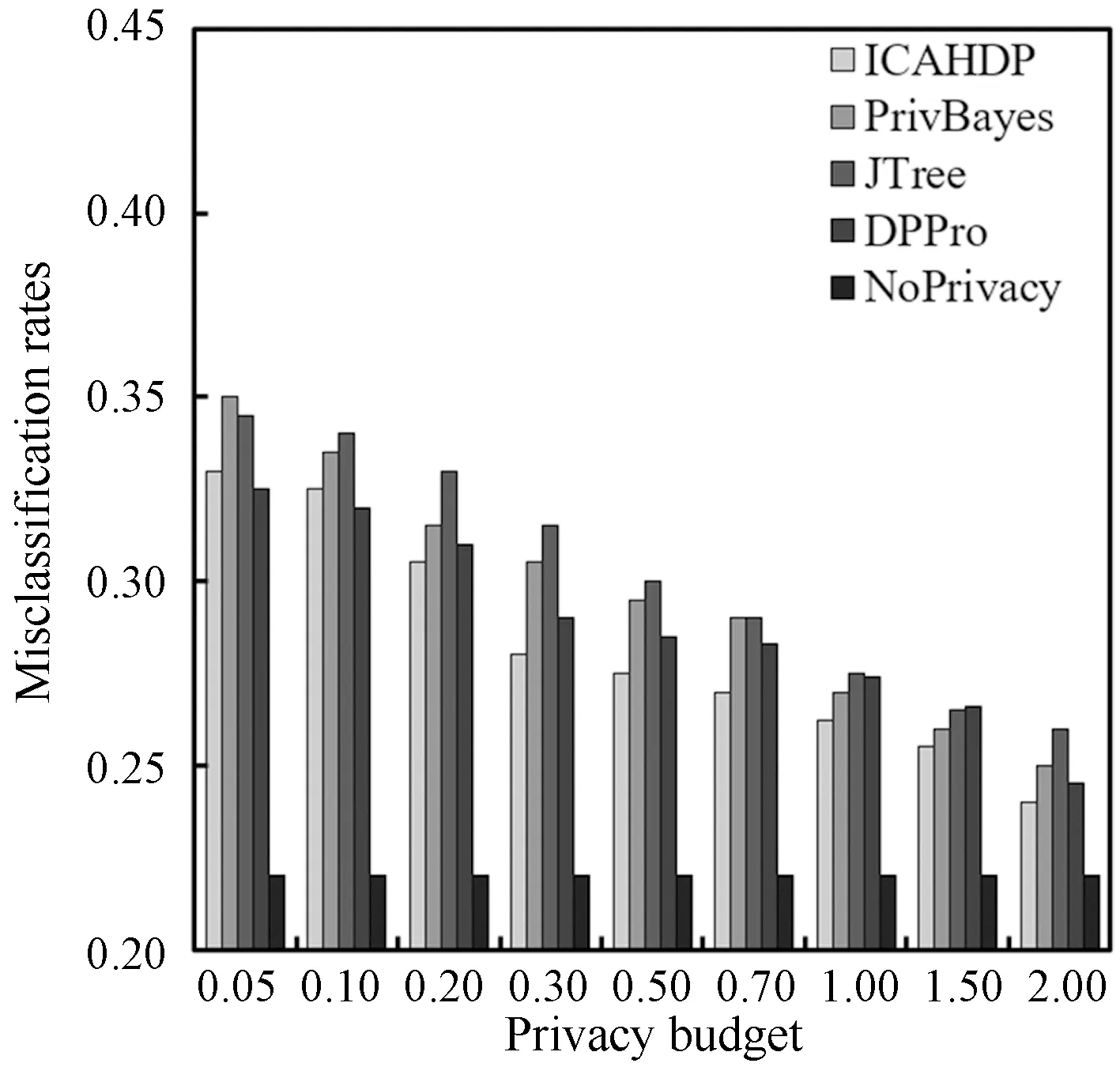
5 结 语

