实用随机多变量NARMAX模型的无模型自校正控制器

侯小秋, 李丽华

黑龙江科技大学 电气与控制工程学院, 黑龙江 哈尔滨 150022

文献[1]利用风机变桨系统的在线I/O数据,在不依赖于被控系统任何数学模型信息的基础下,实现变桨控制并设计了执行器的容错控制策略,以保证风电机组在风速超过额定风速工况条件时的稳定和可靠运行。文献[2]在分析永磁同步电机转速环与电流环超局部模型基础上,构造了无模型滑模速度控制器和电流控制器,并采用滑模扰动观测器对未建模量进行估计补偿,构成了基于滑模扰动观测器的永磁同步电机无模型滑模控制调速系统。文献[3]以四旋翼飞行仿真器作为研究对象,将无模型自适应预测控制应用于四旋翼飞行仿真器的姿态调整控制问题中。文献[4]提出了一类实用多变量NARMAX模型并研究其多变量非线性递推最小二乘法。文献[5]研究了实用单变量随机NARMAX模型的无模型自校正控制器,本文将其推广到多变量情形,研究实用随机多变量NARMAX模型的BP神经网络辨识参数的无模型自校正控制器。

1 实用随机多变量NARMAX模型的泛模型

文献[4]提出实用随机多变量NARMAX模型:

(1)

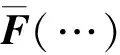
(2)

式中,yF(t)为无干扰输出向量。记输入输出集合M(t)=[y(t-1),y(t-2),…,y(t-ny),u(t-d),u(t-d-1),…,u(t-d-nu)]。

参考文献[6-7]给出yF(t)的具有辅助向量多变量全格式动态线性化方法的泛模型逼近为

(3)

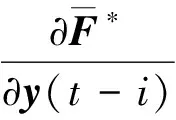
(4)

(5)

V[M(t-1)]=ψ(t),

(6)

则由式(3)—(5)写成

A(q-1)=F1[M(t)]+F2[M(t)]q-1+…+FLy[M(t)]q-(Ly-1),

(7)

B(q-1)=G0[M(t)]+G1[M(t)]q-1+…+GLu-1[M(t)]q-(Lu-1),

(8)

由式(3)、(7)、(8)得

ΔyF(t)=A(q-1)Δy(t-1)+B(q-1)Δu(t-d)+V[M(t-1)],

(9)

把式(9)代入式(1)得

y(t)=yF(t-1)+A(q-1)Δy(t-1)+B(q-1)Δu(t-d)+

(10)

由式(1)、(2)得

(11)

式(11)代入式(10)得

y(t)=y(t-1)+A(q-1)Δy(t-1)+B(q-1)Δu(t-d)+

(12)

式(12)整理得

Ay(q-1)y(t)=Bu(q-1)Δu(t-d)+S(t)+C(q-1)e(t),

(13)

式中,矩阵多项式Ay(q-1)=A′(q-1)-A′(q-1)A(q-1)q-1,Bu(q-1)=A′(q-1)B(q-1),广义辅助向量S(t)=A′(1)V[M(t-1)]/Δ。

2 自校正控制器

2.1 预测模型

由式(13)迭代建立预测模型(忽略C(q-1)e(t)的作用):

(14)

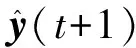
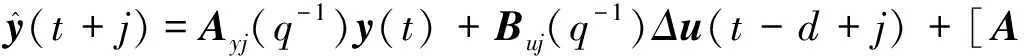
(15)

式中,Ayj(q-1)=Ay1(q-1)Ay(j-1)(q-1),Buj(q-1)=Ay1(q-1)Bu(j-1)(q-1)q-1+Bu(q-1),且Ay0(q-1)=I,Bu0(q-1)=0。

令j=d,得

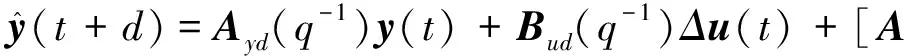
(16)

2.2 自校正控制器算法

广义多变量控制目标函数:

(17)

u(t)=[Bud0+λ0]-1{r(t+d)-Ayd(q-1)y(t)-[Ay1(1)]d-1S(t)-

(18)

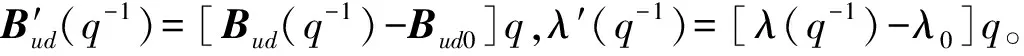
3 BP神经网络辨识

3.1 优化估计模型

干扰模型为

(19)

式中,ξ(t)为干扰向量,且ξT(t)=[ξ1(t),ξ2(t),…,ξn(t)],式(19)转化为

(20)

(21)

(22)

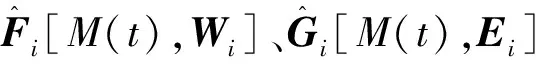
(23)

(24)

且

则由式(21)可得

且

由式(22)可得

且

3.2 梯度表达式

由式(24)控制器参数向量

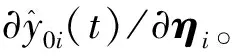
(25)

(26)

(27)

(28)

(29)

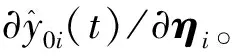
3.3 ηi的学习及估计算法

选取目标函数

(30)

(31)

算法式(30)、(31)的矩阵求逆和克服算法病态λi(t)的确定由文献[4]的算法实现。

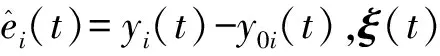
4 仿真研究

被控对象

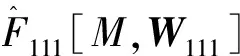
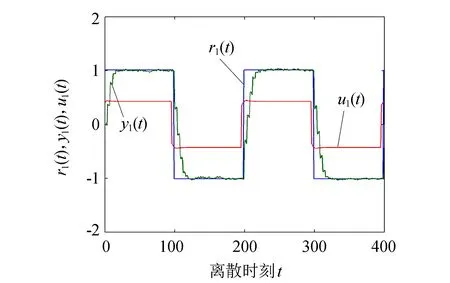
图1 响应曲线

5 结论

1)本文提出了模型形式未知的实用随机多变量NARMAX模型的具有辅助向量的多变量全格式动态线性化方法逼近的泛模型,构建了多变量预测模型,计算了输出预测向量;

2)采用BP神经网络辨识泛模型参数函数,增加了参数函数的信息含量;

3)通过非线性递推最小二乘法对BP神经网络的连接权重值进行学习,同时估计随机干扰模型的参数,提出了新的学习算法;

4)基于改进多变量广义控制目标函数和该泛模型,提出了BP神经网络辨识泛模型参数函数的无模型自适应多变量自校正控制器。