基于水体导电特性的电流信号传输研究

李盛洪, 金建辉, 汪 洋

1.昆明理工大学 信息工程与自动化学院, 云南 昆明 650504;2.中国船舶集团有限公司第七〇五研究所, 云南 昆明 650032

水文工作涉及防汛抗旱减灾、水资源开发与利用以及水生态保护。水资源数据收集和整理,天然河流的流速、流量、含沙量等信息的采集对水利工程建设、水资源管理与保护、防汛抗旱、水质改善等具有重大意义[1-2]。在水文缆道信号传输系统中,水体和缆道构成电流信号传输的回路。目前国内外的采集测验方法主要有涉水测法、船测法、桥测法和缆道测法[3],其中缆道测法是利用跨河缆道系统将测验平台运送到测验断面的指定垂线和测点处,由测验平台测量数据并通过缆道与水体组成的回路将数据传输到水文测站,它是国内最主要、最有效的水文信息测验技术[4]。由于地理因素和社会环境的影响,国外主要采用桥测法,对缆道测法的研究与应用极少。国内对缆道测法的研究最早开始于20世纪80年代,鲍德安[5]指出水文缆道信号传输利用缆道和水体构成通道,即水文测量工作中习称的无线测流,提出了缆道信号传输的技术处理,即在信号线上提高绝缘度、降低接地电阻。刘志亭[6]重点讨论了绝缘处理对缆道信号的影响;姜洪鼎[7]认为需要和环境有机结合;肖虎程等[8]将DSP技术应用到水文缆道测流信号处理;Zhu Bing等[9]提出了一种嵌入式水文缆道测控系统;韦连元[10]初步建立了不绝缘的缆道信号传输回路的等效电路;戴建国[11]提出了缆道的交流等效概念;刘泽文等[12]对水文缆道信号传输的基本原理和方法做了探讨;张义鑫[13]建立了缆道水体信道的等效电路,明确信道中存在等效电容和等效电感;李盛洪等[14]研究出一种功率可调的隔离型水文缆道信息高可靠性传输系统;梁奇兵等[15]提出一种利用水介质导电特性的水下信号传输方法,但仅认为水介质具有电阻特性。截至目前,水文缆道测法已发展了数十载,研究人员对水体导电特性的理论研究较少,侧重于应用,但缆道信号传输不可靠。本文将基于黑箱理论对水体的导电特性进行分析,进一步提高水文缆道电流信号传输的可靠性。

1 模型建立

水体环境复杂,不仅存在电极产生的极化效应、电容效应、温度效应,而且存在电磁场、压力场以及各种物理场的影响[16-17],导致水体的导电特性呈现出动态非线性,并且对于信号的频带分析无法用现有的理论进行分析,因此本文将采用黑箱建模方法对水体进行建模。黑箱方法就是不打开黑箱,利用外部观测、试验,通过输入、输出信号来研究黑箱的功能和特性,探索其构造和机理的科学方法[18]。

基于黑箱理论建立一个长方体的水体,通过两块导电极板连接到回路中,由激励源ui产生电流信号通过水体传输到纯电阻负载RL上,从而分析水体作为通信回路中一条支路的传输特性。研究模型的通信回路如图1所示。

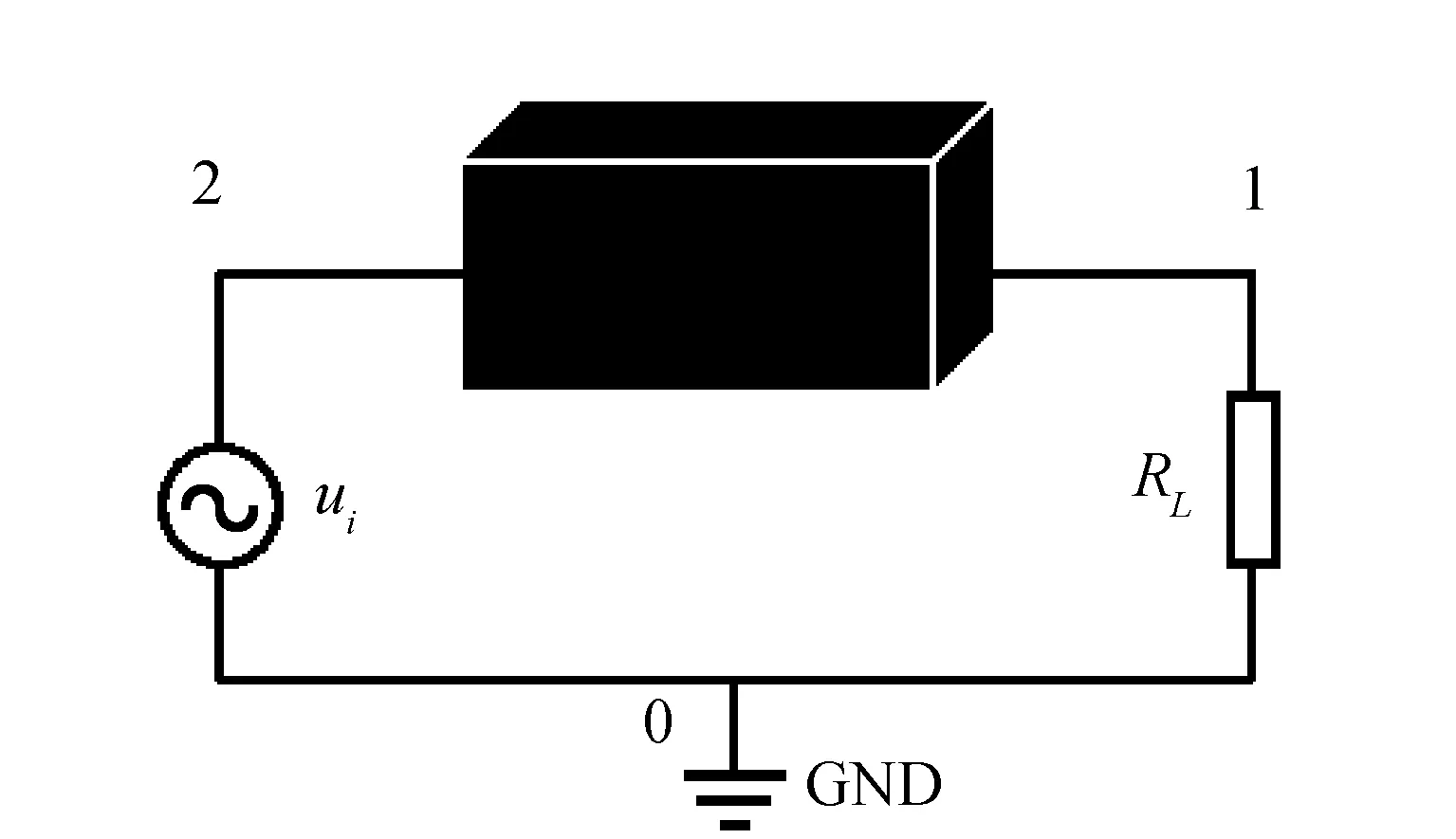
图1 研究模型的通信回路

COMSOL Multiphysics是一款大型的高级数值仿真软件,可以模拟科学和工程领域的各种物理过程,以高效的计算性能和杰出的多场双向直接耦合分析能力实现高度精确的数值仿真[19-20]。有限元法(Finite Element Method,FEM)是一种为求解偏微分方程边值问题近似解的数值技术,求解时对整个问题区域进行分解,使得每个子区域都成为简单的部分,这种方法广泛应用于求解电磁场、流体力学、热传导等问题[21-22]。水体的分析采用有限元法具有较好的优势,可以较为完整的分析出水体特性。

采用有限元仿真软件COMSOL对80 cm×35 cm×20 cm体积的水体进行传输信号仿真分析,仿真模型如图2所示。

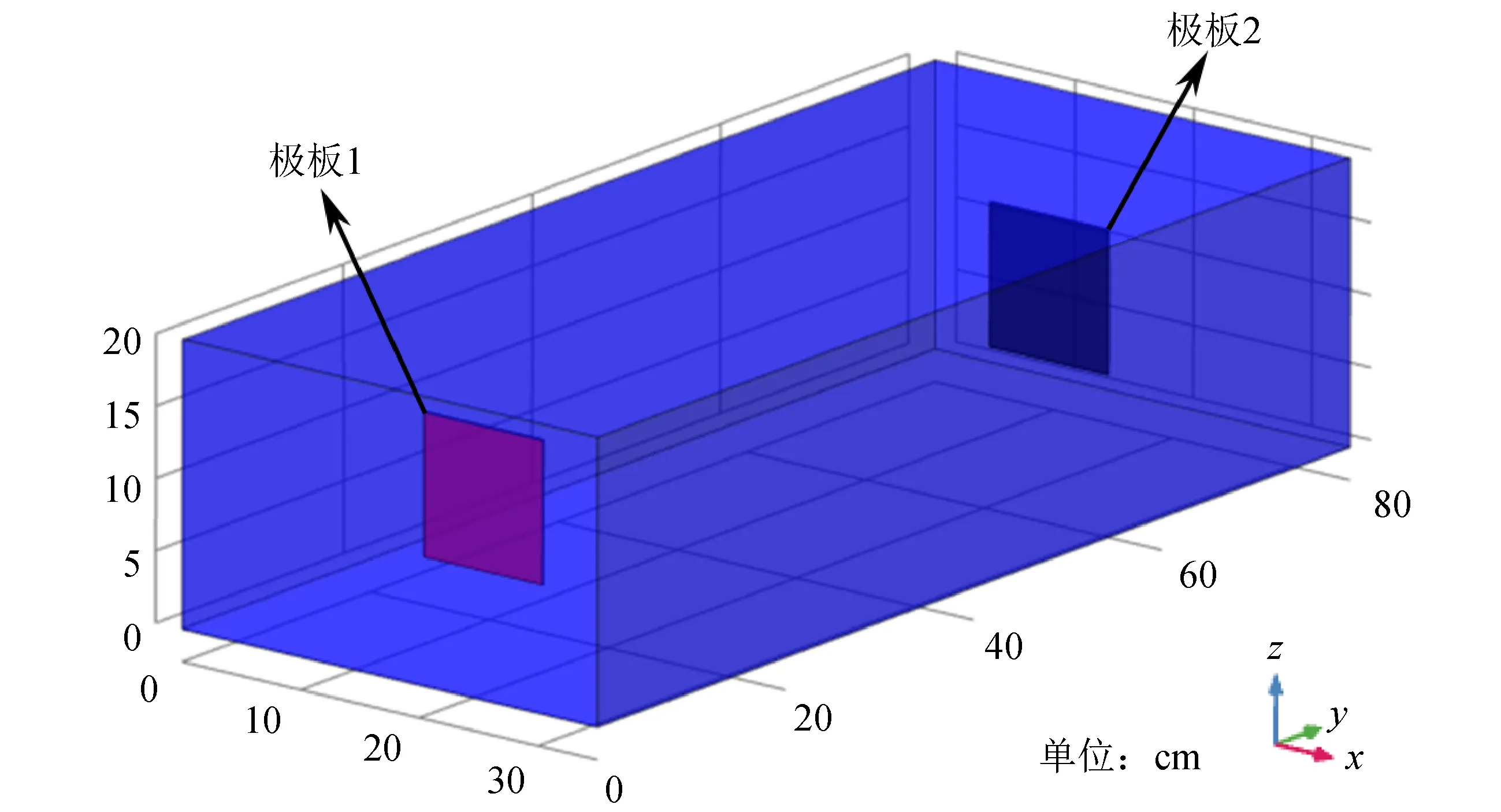
图2 仿真模型

2 传输特性分析

2.1 理论分析

激励源会在水体中产生电荷,电荷会产生电场,电场会使水体中的阴阳离子做定向运动,电荷运动会产生电流,电流会产生磁场。媒质对电磁场的响应主要是传导、极化、磁化。首先,电场会导致水体中自由电子移动,进而形成传导电流[23-25]。电流密度矢量Jc和电场强度E成正比,与水体的电导率σ有关,公式为

Jc=σE。

(1)

其次,电流会产生磁场,在介质中电场会引起极化,形成位移电流[26],位移电流Jd表示电场的变化率,等于电位移矢量D随时间t的变化率,与水体的介电特性有关,公式为

(2)

因此在水体中存在传导电流和位移电流,满足电流守恒方程,公式为

(3)

采用有限元仿真软件COMSOL基于此方程进行仿真,并且COMSOL水体模型的边界条件为第一类边界条件(Dirichlet)。

2.2 有限元仿真分析

本文使用有限元软件COMSOL建模分析,选择电流(ec)物理场,电流用于计算导电介质中的电场、电流及电势分布。几何建模一个80 cm×35 cm×20 cm的长方体作为水体,材料属性设置为自来水;几何建模两个极板,材料属性设置为铜;不同水质的水体和极板材料可以修改相关参数。极板1定义为正极板,极板2定义为负极板,见图2。

2.2.1 水体模型频域特性仿真

极板1设置为终端,终端类型选择电压,极板2设置为接地。水的相对介电常数εr=81,利用E-1便携式TDS&EC测试笔测得自来水的电导率σ=184 μS/cm(仿真中统一使用此电导率)。

1)结合实际测试条件,采用控制变量法在极板距离(L=60 cm)、极板面积(S=10 cm×10 cm)相同的情况下改变传输信号频率对水体进行有限元仿真,仿真结果如图3所示,部分仿真数据见表1。

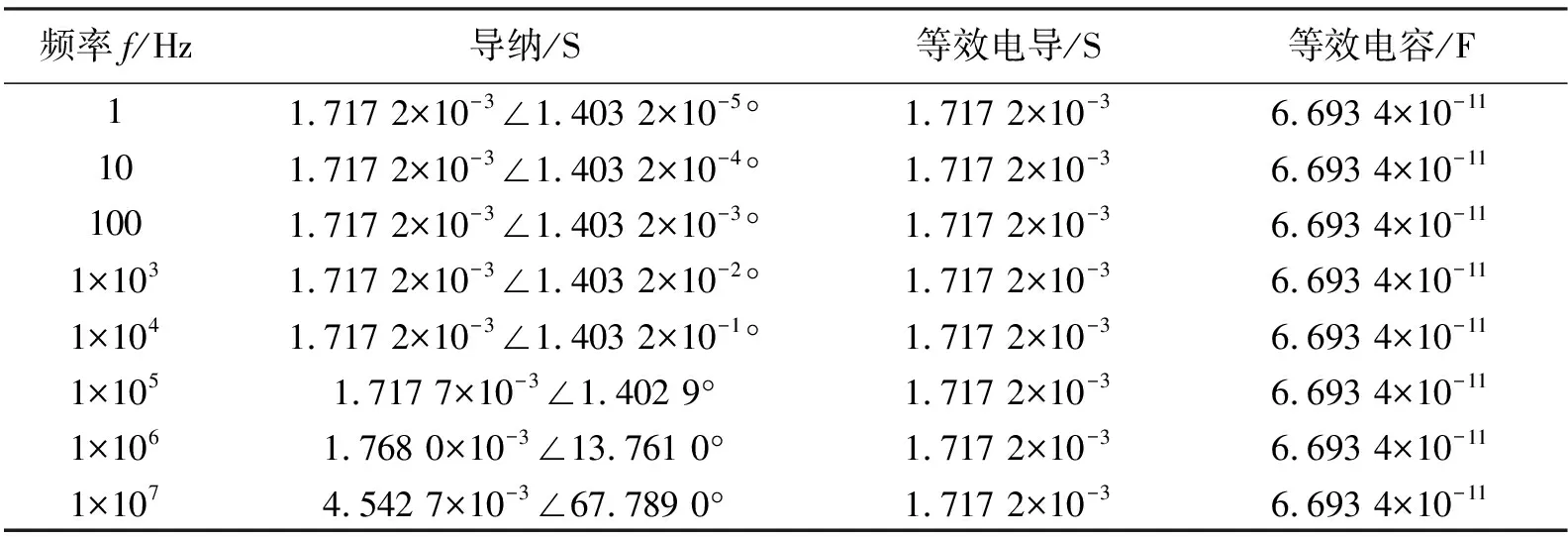
表1 不同频率的频域仿真数据

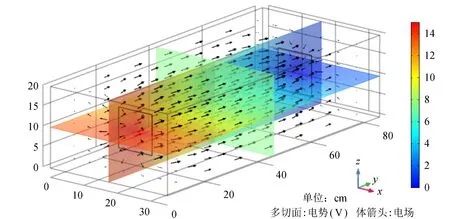
图3 频域仿真

图3中箭头为电场方向,切面为电势,由图可以看出极板1周围的电场强度最强,极板2周围的电场强度最弱,并且极板1所有面都有电荷流出,经过水体流入极板2的所有面。仿真结果表明:随着传输信号频率的增大,导纳角和导纳模增大,其中等效电导和等效电容不变。

2)结合实际测试条件,采用控制变量法在传输信号频率(f=1 kHz)、极板面积(S=10 cm×10 cm)相同的情况下改变极板间距离对水体进行有限元仿真,部分仿真数据见表2。

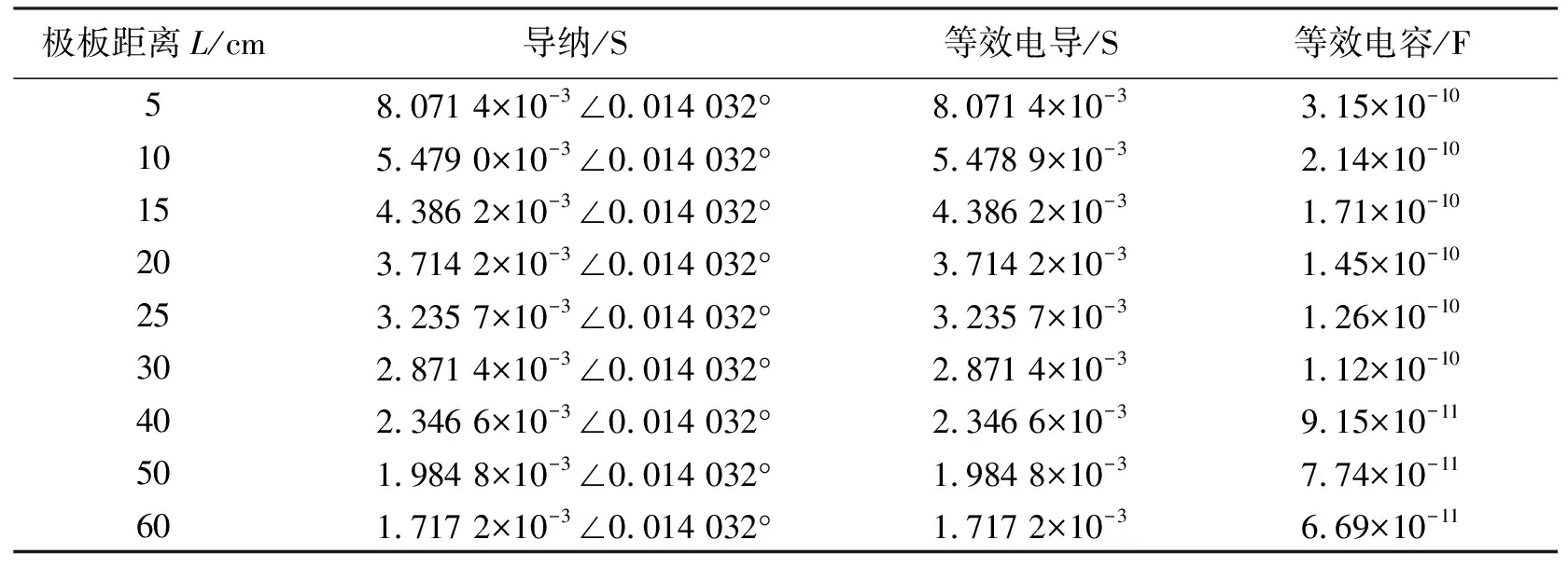
表2 不同极板距离的频域仿真数据

仿真结果表明:随着极板间距离的增大,导纳角不变,导纳模减小,其中等效电导和等效电容减小。

3)结合实际测试条件,采用控制变量法在传输信号频率(f=1 kHz)、极板距离(L=60 cm)相同的情况下改变极板面积对水体进行有限元仿真,部分仿真数据见表3。

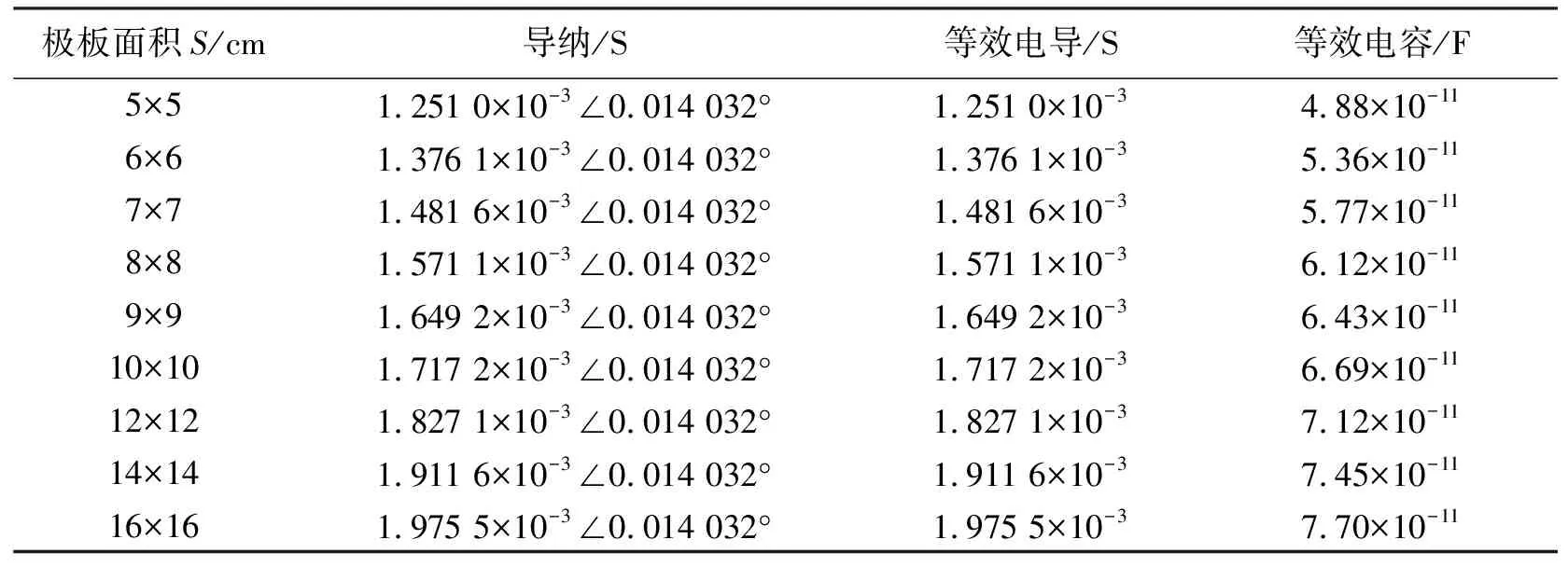
表3 不同极板面积的频域仿真数据

仿真结果表明:随着极板面积的增大,导纳角不变,导纳模增大,其中等效电导和等效电容增大。

综上所述,可以得到如下结论:

①导纳模随着传输信号频率的增大而增大,随着极板间距离的增大而减小,随着极板面积的增大而增大;

②导纳角随着传输信号频率的增大而增大,与极板距离和极板面积无关;

③等效电纳和等效电容与传输信号频率无关,随着极板距离的增大而减小,随着极板面积的增大而增大。

2.2.2 模型整体瞬态仿真

利用COMSOL的“电路(cir)”物理场和“电流(ec)”物理场对模型进行整体回路瞬态仿真。“电流”物理场中将终端类型设置为电路,连接到电路接口中的外部IVS.U特征;“电路”物理场中将接地设置为0节点,激励源正极设置为2节点,负极设置为0节点,水体极板1设置为2节点,极板2设置为1节点,负载电阻RL两端分别设置为0和1节点,见图1。

激励源设置为正弦交流电压源,Vp=15 V,f=1 kHz,RL=1 Ω,整体模型瞬态仿真波形图如图4所示。因为RL=1 Ω,所以RL上的电压波形可以代替流过水体的电流波形,方便观测。

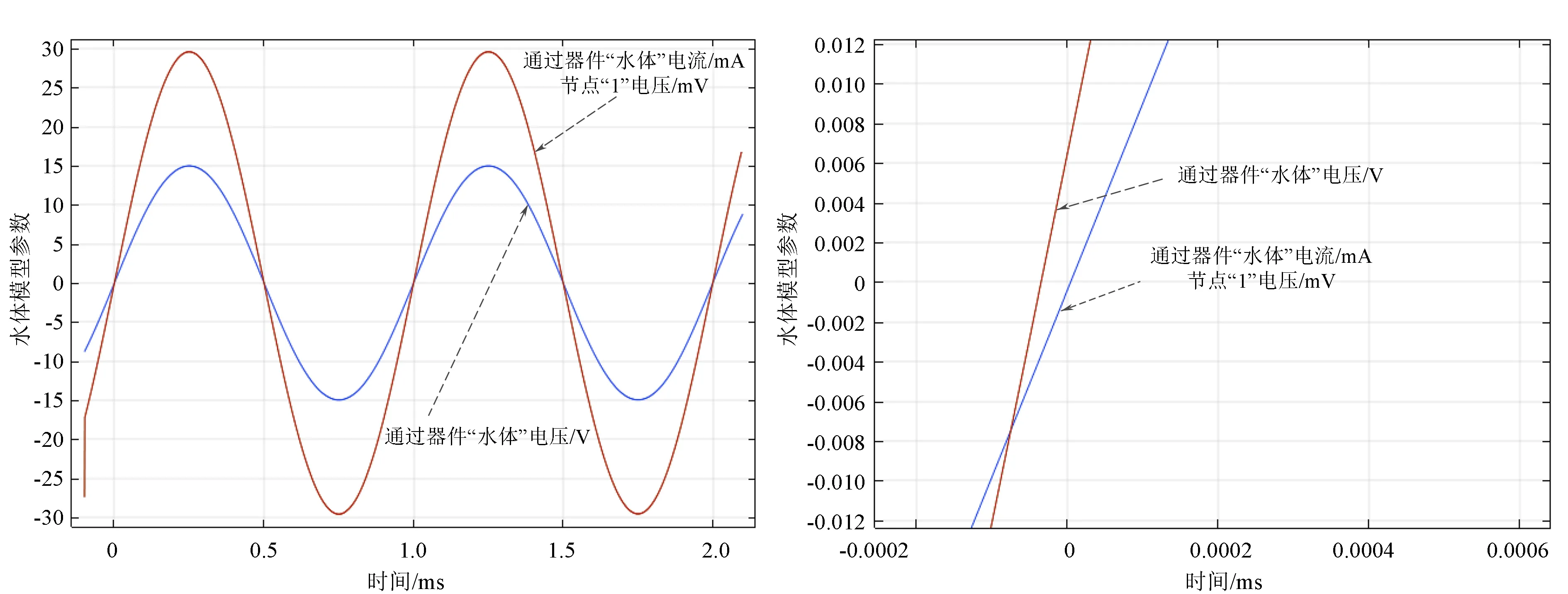
图4 模型整体回路瞬态仿真波形 图5 模型整体回路瞬态仿真局部放大波形

将波形图放大,如图5所示,可以明显看出电流波形超前电压波形,水体呈容性电纳,与前文分析相符。

1)结合实际测试条件,采用控制变量法在极板距离(L=60 cm)、极板面积(S=16 cm×16 cm)相同的情况下改变传输信号频率对模型进行整体回路瞬态仿真,部分仿真数据见表4。

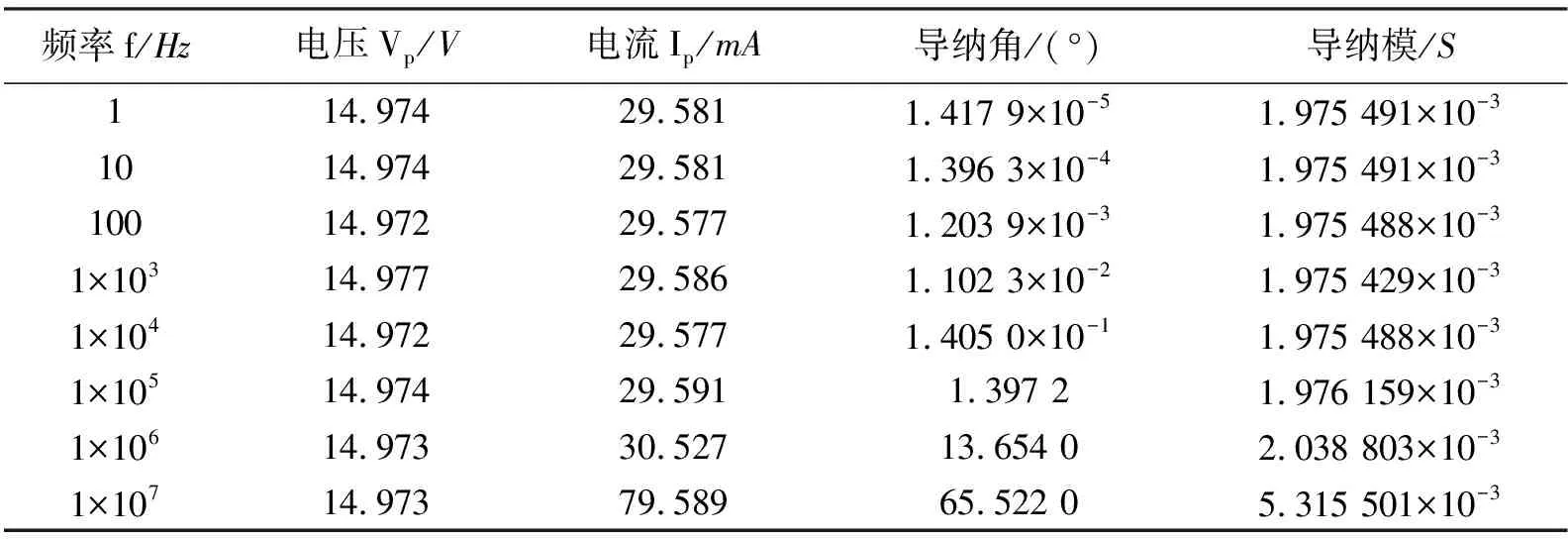
表4 不同频率的模型瞬态仿真数据

2)结合实际测试条件,采用控制变量法在传输信号频率(f=1 kHz)、极板面积(S=16 cm×16 cm)相同的情况下改变极板间距离对模型进行整体回路瞬态仿真,部分仿真数据见表5。

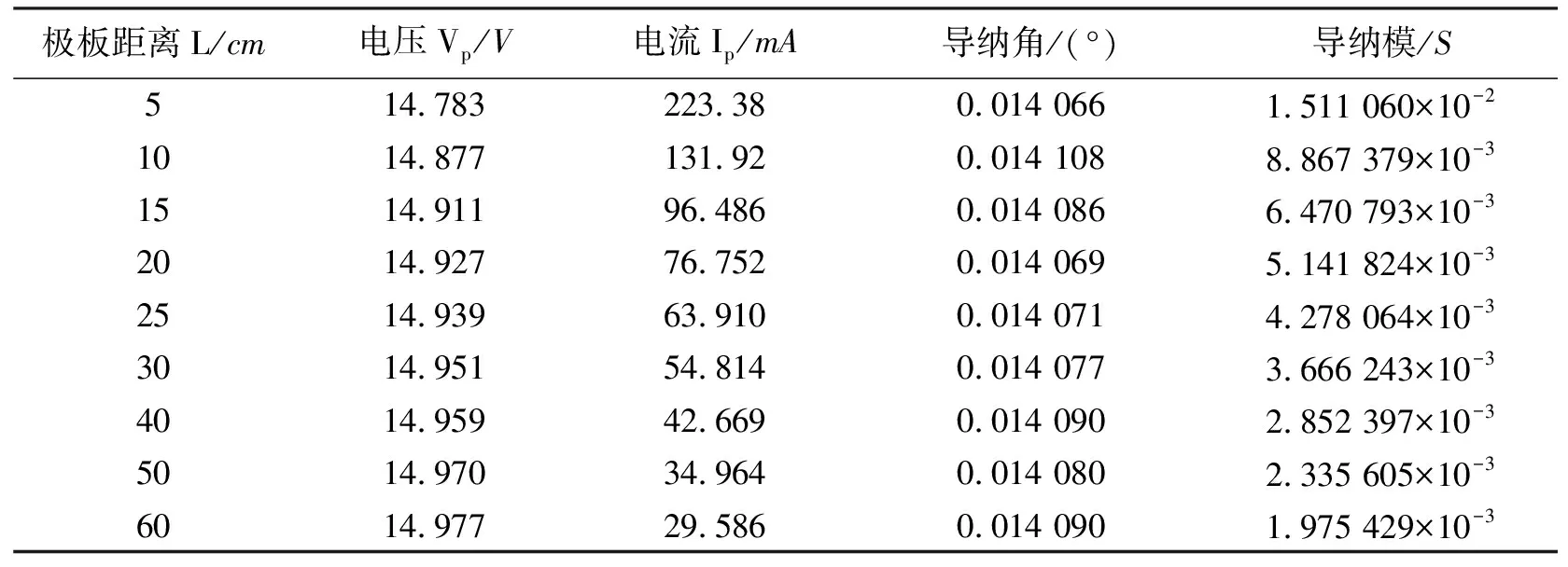
表5 不同极板距离的模型瞬态仿真数据

3)结合实际测试条件,采用控制变量法在传输信号频率(f=1 kHz)、极板距离(L=60 cm)相同的情况下改变极板面积对模型进行整体回路瞬态仿真,部分仿真数据见表6。

表6 不同极板面积的模型瞬态仿真数据

上述瞬态仿真结果与频域仿真结果一致,从而证明了整体回路模型的可行性。

2.3 等效模型分析

根据理论分析和有限元仿真可将水体等效为一个一端口网络,在相量法中,可以用等效参数复阻抗或者复导纳来表述水体的对外特性,本文采用复导纳进行分析。复导纳Y=G+jB,G为等效电导分量,B为等效电纳分量,水体的等效电路用等效电导和一个储能元件并联表示,通过理论分析和仿真分析可知,水体的等效电纳B>0,因此水体的等效电纳为容性电纳,可以用等效电容Ceq代替,等效公式为

Y=G+jωCeq,

(4)

等效模型如图6所示。

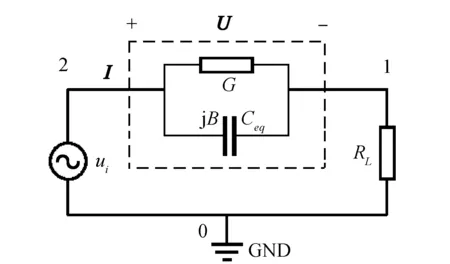
图6 等效模型

根据公式(4)可以得到水体的导纳模|Y|以及阻抗角φY分别为

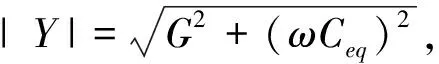
又因为理想情况下电导的关系式为G∝σS/L,电容的关系式为C∝εS/L,其中介电常数ε=ε0εr,ε0=8.86×10-12F/m。但由于水体环境复杂,所以需要对关系式进行修正,即G=kGσS/L,C=kCε0εrS/L,其中kG、kC均为修正系数。通过对有限元仿真和实验测试数据的拟合分析得到kG和kC的取值范围为2.19～16.32,取值原则:随着极板间距离的增加,kG和kC的取值相对越大,随着极板面积的增大,kG和kC的取值相对越小。因此在实际情况下公式(5)和公式(6)分别可以变换为

(7)

(8)

根据公式(7)可知:f增大,|Y|增大;L增大,|Y|减小;S增大,|Y|增大;结果与结论①相符。根据公式(8)可知:f增大,φY增大;φY与L和S无关;与结论②相符。

根据上述分析,可得负载上的电压为

(9)

3 实验结果与分析

实测模型采用一个80 cm×35 cm×50 cm的玻璃水池,导电极板采用规则的薄铜板。实验测试注入20 cm高的自来水。由于水体测试环境在改变,电导率会发生微小改变,但对于单一控制变量的分析没有影响。

1)信号源设置为正弦交流信号,Vpp=20 V,RL=1 Ω,在极板距离(L=60 cm)、极板面积(S=10 cm×10 cm)相同的情况下改变传输信号频率对模型进行整体实测,测试时利用E-1便携式TDS&EC测试笔测得自来水的电导率σ=204 μS/cm,温度T=22 ℃,模型部分实测波形图如图7所示。图中CH1通道为水体两端的信号电压波形,CH2通道为RL上的信号电压波形(示波器参考点为图1中节点1,为了方便观测,示波器CH2通道波形设置为反向),可以视为流过水体的电流波形。部分实测数据见表7。由于信号源的输出功率有限,当频率过高时,无法正常输出设定值,因此信号源的输出会改变,但是不影响本模型的测试。当频率小于10 kHz时,由于示波器仪器的原因,导纳角无法测量。

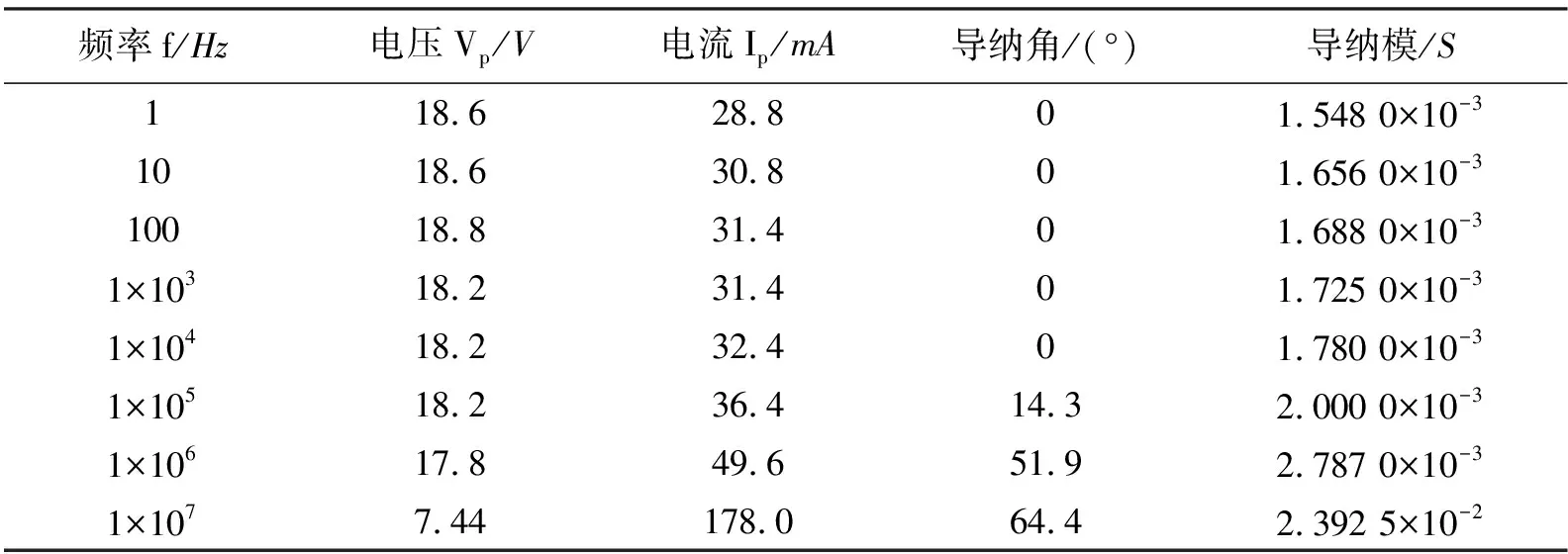
表7 不同频率模型的部分实测数据

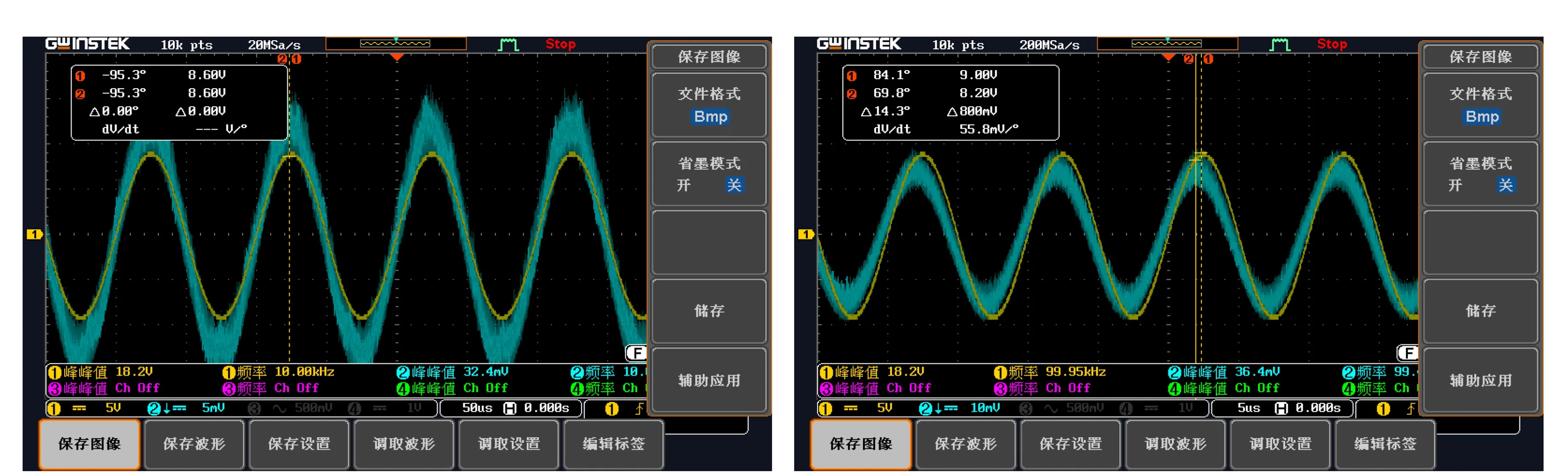
(a) f=10 kHz (b) f=100 kHz

2)在频率(f=100 kHz)、极板面积(S=10 cm×10 cm)相同的情况下改变极板间距离对模型进行整体实测,测试时利用E-1便携式TDS&EC测试笔测得自来水的电导率σ=182 μS/cm,温度T=20.4 ℃。部分实测数据见表8,模型部分实测波形图如图8所示。

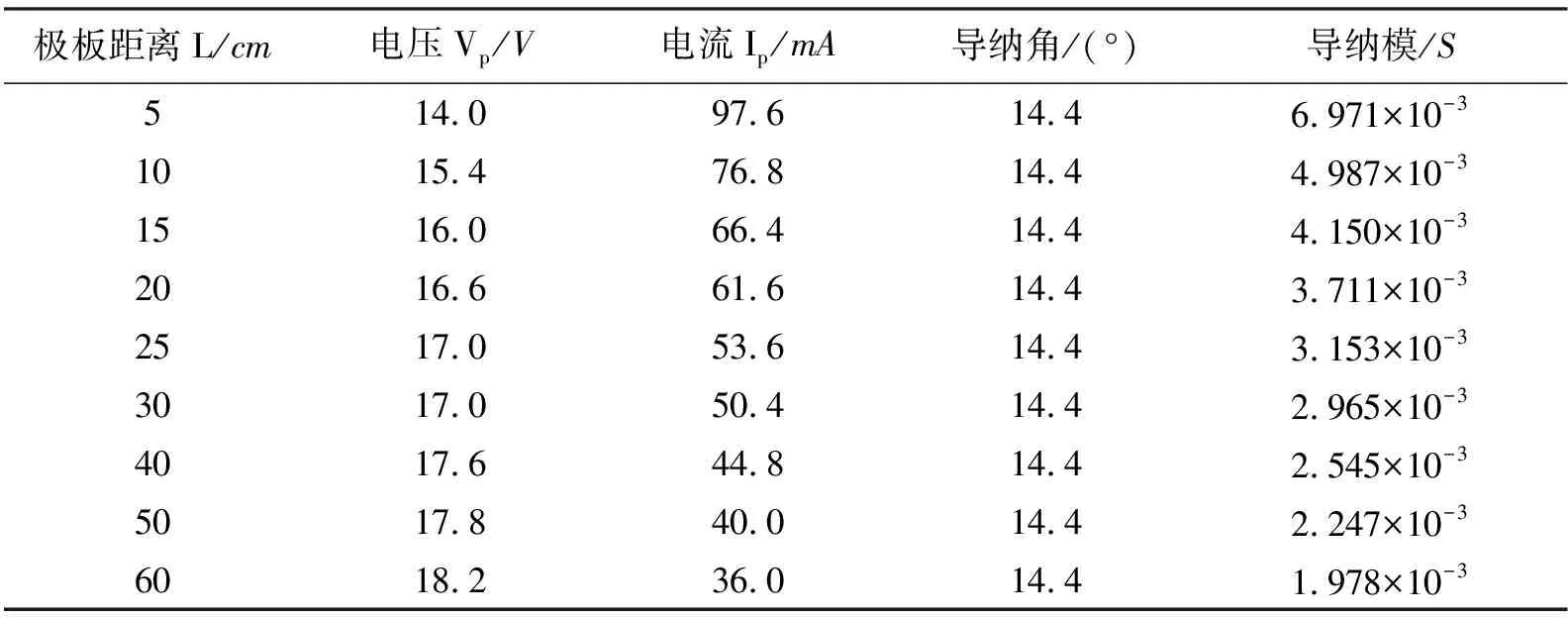
表8 不同极板距离模型的部分实测数据

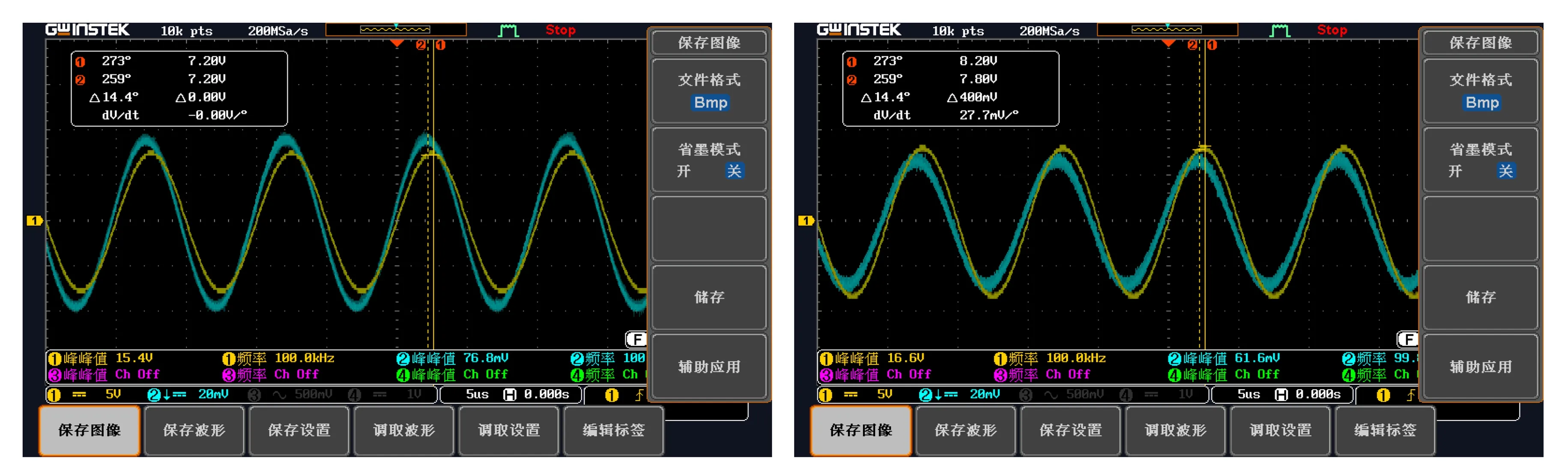
(a) L=10 cm (b) L=20 cm

3)在传输信号频率(f=100 kHz)、极板距离(L=60 cm)相同的情况下改变极板面积对模型进行整体实测,测试时利用E-1便携式TDS&EC测试笔测得自来水的电导率σ=220 μS/cm,温度T=20.0 ℃。模型部分实测波形图如图9所示,部分实测数据见表9。

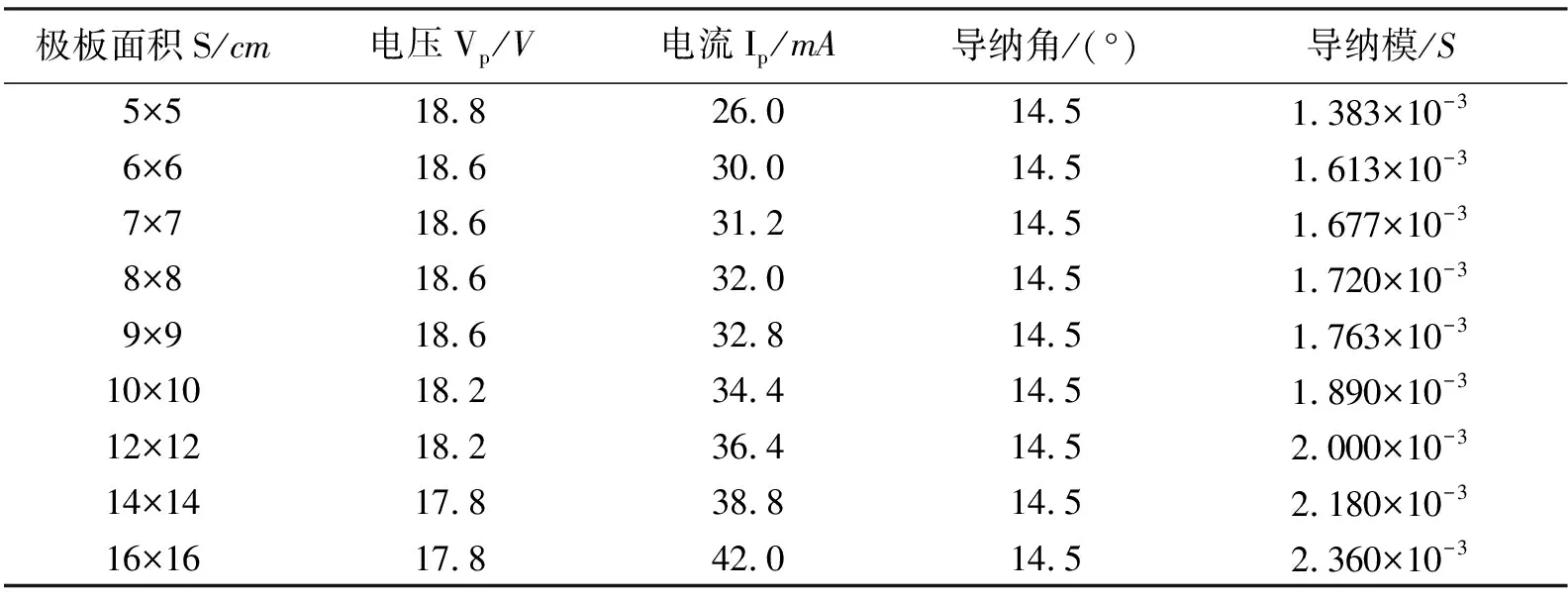
表9 不同极板面积模型的部分实测数据

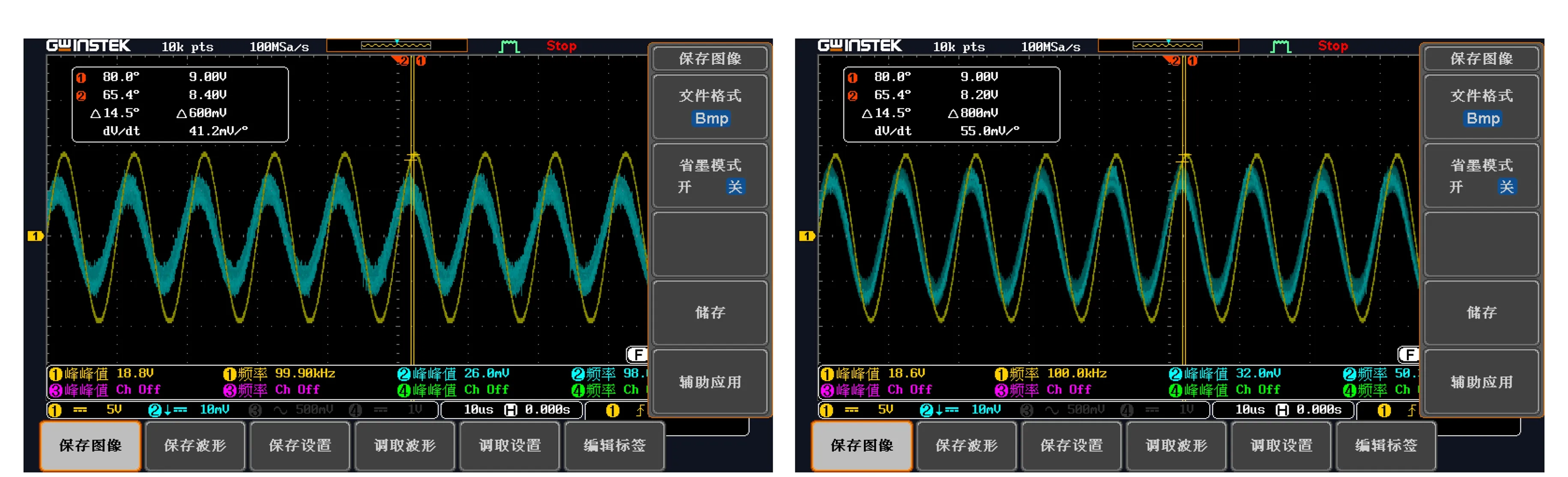
(a) S=5 cm×5 cm (b) S=8 cm×8 cm

上述实验结果与有限元仿真分析、等效模型分析相符,有效地证明了模型的准确性。

根据公式(7)—(9)可以推导出负载上得到的电压uRL与激励源ui、传输信号频率f、极板距离L、极板面积S、电导率σ以及相对介电常数εr的关系式如下:

(10)

根据公式(10)可知:f增大,uRL增大;L增大,uRL减小;S增大,uRL增大。综上可以得到,增大传输信号的频率、减小极板距离、增大极板面积均有利于电流信号的传输。

4 结论

本文基于黑箱理论利用有限元仿真软件COMSOL对水体作为电流通信回路中的一条支路的水体导电特性进行研究和分析,通过对水体进行模型建立、仿真、等效、实验和分析,提出等效模型,并通过分析信号传输频率、极板距离、极板面积等参数对通信回路中信号传输特性的影响,得出一个简化的计算公式,为相关领域的研究人员提供了一个参考。在后续研究工作中,我们将继续对模型进行优化和完善,推导和分析出一个更完整、严谨、科学的结论。