轨道车辆制动防滑控制系统数值建模与验证

朱文健,余朝刚,朱文良

(上海工程技术大学 城市轨道交通学院,上海 201620)

轨道车辆制动系统是影响列车运行安全的关键系统之一。黏着制动需要依靠轮轨间的黏着力来实现,当车轮制动力大于轮轨间所能提供的最大黏着力时,列车就会发生滑行;特别是在低黏着工况下,若不有效控制制动力,将会造成车轮踏面擦伤,影响列车的运行安全。因此为了有效防止轮对出现滑行,防滑器应运而生[1-2]。防滑阀作为防滑器中的关键部件之一,其性能好坏直接影响防滑装置的可靠性及稳定性。近年来,国内外学者对防滑阀建模及防滑控制特性进行了很多研究。李邦国等[3]采用AMESim仿真平台建立了防滑阀模型,并进行了防滑阀节流孔参数变化对充排风影响的仿真分析;胡晓峰等[4]建立了防滑阀数值模型并搭建了防滑阀检测试验台,通过测试其动特性与实测曲线对比验证了仿真模型与测试系统的精度,为防滑阀结构优化提供了合理的方法;Luo等[5]建立了一种用于地铁列车的制动系统模型,能够准确地预测制动系统特性,并解释了压力误差产生的原因;Zhu等[6]基于AMESim建立了空气制动防滑阀类模型,利用MATLAB/Simulink搭建了车辆动力学模型和轮轨黏着模型,通过联合仿真的方法对轨道列车制动防滑特性进行了仿真分析;Turabimana等[7]通过对防滑控制系统建模及仿真,研究了列车行过较小曲率半径线路时滑移率及制动力变化,为防止车轮发生纵向及横向滑行带来轮缘磨损提供参考;刁锋等[8]建立了轨道车辆动力学模型、轮轨黏着模型和制动系统气路模型,构建虚拟列车运行环境,分析对比了不同轮轨黏着条件以及不同制动初速等工况在内的各滑行试验典型工况。Zhu等[9]通过建立单轮防滑控制系统联合仿真模型来探讨滑移判据的优劣,得出列车轮对减速度和减速度微分作为防滑判据能使列车防滑效果更好。以上学者们对防滑阀及防滑控制进行了相关研究,为列车防滑仿真建模提供了设计参考。

本文在上述研究基础上进行了防滑阀数值建模及验证,并结合制动防滑控制仿真平台进行了防滑控制性能研究。首先基于防滑阀工作原理建立了数学模型,依据文献[3]中测试方法及指标要求和TB/T3009-2019《机车车辆制动系统用防滑装置》[10]等标准验证了模型的正确性;然后搭建了四轴车辆制动防滑控制数值仿真平台,并按照标准EN15595[11]中相关要求,将仿真结果与实车试验结果进行对比,结果表明两者吻合良好, 验证了制动防滑控制数值仿真平台的有效性。

1 防滑阀结构与原理

防滑阀是轨道车辆制动系统的重要阀件之一,是防滑控制回路中的执行机构。常见三位式防滑阀结构如图1所示,构成主要包括:进气电磁阀(Hold valve,HV)、、排气电磁阀(Release valve,RV)及进排气膜片。防滑阀通过指令接收端VM1、VM2分别控制双电磁阀励磁线圈电压的通断,动铁芯移动后,通过进排气膜片阀口的开闭分别控制进气口、出气口及排气口的通断,以实现防滑阀的进气、保压及排气功能。

图1 防滑阀结构示意图Fig.1 Diagram of anti-skid valve structure

当列车无滑行产生时,防滑控制单元不发出防滑指令信号,此时防滑阀的作用相当于管路;当防滑控制单元检测到列车发生滑行并发出防滑指令信号时,防滑阀的励磁线圈得电,使其电磁铁铁芯运动,通过改变防滑阀内的空气管路通断,以实现防滑功能。

2 防滑阀数学模型与性能验证

防滑阀作为一种气控型高速电磁阀,主要包含电磁部分、机械动力部分及腔室充排气部分,形成一个强耦合系统,耦合关系如图2所示。

图2 防滑阀数值模型耦合图Fig.2 Diagram of numerical model coupling of anti-skid valve

为便于数值建模与仿真,作出如下假设[12-13]:

1) 空气压力源、电磁阀控制电压均恒定且稳定;

2) 忽略电、磁路中电阻、磁阻变化;

3) 忽略阀体内部温度变化且阀体无泄漏。

2.1 防滑阀数学模型

2.1.1 电磁部分

当电磁阀励磁线圈得电时,动铁芯在电磁力作用下产生移动,由基尔霍夫电压定律可得:

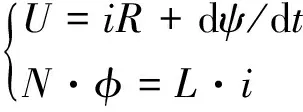
(1)

式中:U为电磁阀励磁电压;i为线圈电流;R为线圈电阻;ψ为电磁部分全磁链;N为线圈匝数;φ为磁通量;L为电感。

由磁力、磁能公式及磁路磁动势有:

(2)

式中:F为电磁力;E为电磁部分的磁能;δl为磁路工作气隙最大长度,m;F0为磁路磁动势;Rm为磁路总磁阻,由导磁体磁阻Rdf、经过衔铁的磁阻Rx及磁路中工作气隙磁阻Rδl组成,较之工作气隙磁阻,导磁体磁阻和衔铁磁阻可忽略不计;忽略电磁阀运动引起的气隙变化,可得

(3)

式中:μ0为真空磁导率,μ0=4π×10-7Wb/A·m;

A为工作气隙横截面积,m2。

综合式(1)～式(3)可得电磁力表达式为

(4)

2.1.2 机械部分

机械部分由动铁芯质量、电磁力、气压作用力、动铁芯复位弹簧及运动阻尼组成。

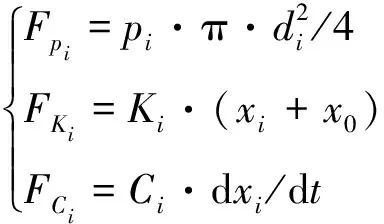
(5)

式中:i取H或R,分别为进气电磁阀或排气电磁阀相关参数;Fpi(FpH、FpR)、FKi(FKH、FKR)、FCi(FCH、FCR)分别为进气阀、排气阀动铁芯所受气压作用力、弹簧力、阻尼力;pi(pH、pR)分别为进气阀、排气阀动铁芯所受气压;di(dH、dR)、xi(xH、xR)分别为进气阀、排气阀动铁芯所受气压作用直径(m)、动铁芯位移(m);Ki(KH、KR)、Ci(CH、CR)分别为进气阀、排气阀动铁芯复位弹簧弹性系数(N/m)、运动阻尼系数(N·s/m);x0为复位弹簧预压缩量(m)。应用牛顿第二定律可得动铁芯位移表达式为

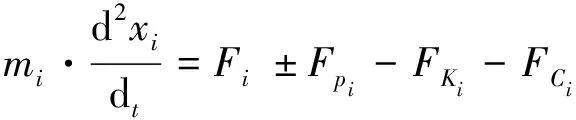
(6)

式中:当i取H时,±号为+,此时表示进气阀动铁芯位移方程;当i取R时,±号取-,此时表示排气阀动铁芯位移方程。

同理,可得进、排气膜片位移方程为

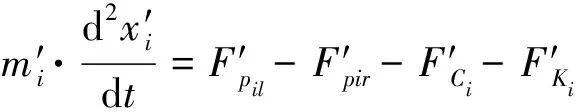
(7)

式中:i取H或R, 分别为进气膜片或排气膜片相关参数;m′i、x′i分别为膜片质量、膜片移动位移;F′pil、F′pir、F′Ci、F′Ki分别为膜片所受左气压力、右气压力、阻尼力、复位弹簧力。表达式分别为:

(8)

式中:当i取R时,F′Ki=0;x1为进气锥形弹簧预压缩量,m。

2.1.3 腔室充排气部分

防滑阀机电部分通过控制阀口开度大小来控制阀口处的气体流量。由于气体流经节流孔时与管壁接触面小、流动快,故可考虑为一维等熵流动。等熵气流流经阀口节流孔的质量流量[5]表达式为:

(9)

(10)

A1=(π/4)·d1(t)2

(11)

式中:A1为流通孔截面积,m2;d1(t)为t时刻节流孔直径,m;pi为输入压力;po为输出压力;γ为气体的比热比,γ=1.4;R0为气体常数,R0=287.13 N·m/(kg·K);T为气体绝对温度,T=313 K;Cq为气流常数,由Peery通过试验测出

根据上述质量流量表达式结合理想气体状态方程可得输入输出压力变化的微分表达式为

(13)

式中V为腔室容积,m3。

2.2 防滑阀仿真模型

基于MATLAB/Simulink分别建立电磁部分仿真模型、机械及气路部分仿真模型,如图3所示。由防滑控制单元指令信号作为输入控制信号,输出信号为制动缸压力,部分仿真参数如表1所示。

表1 仿真模型部分参数Tab. 1 Some parameters of the simulation model

图3 防滑阀Simulink仿真模型Fig.3 Simulink simulation model of anti-skid valve

2.3 仿真模型验证

在完成防滑阀仿真模型建立的基础上,采用文献[3]中测试方法及设计指标进行防滑阀性能验证。测试内容包括:快速充气与阶段排气、阶段充气与快速排气。测试结果图4所示。

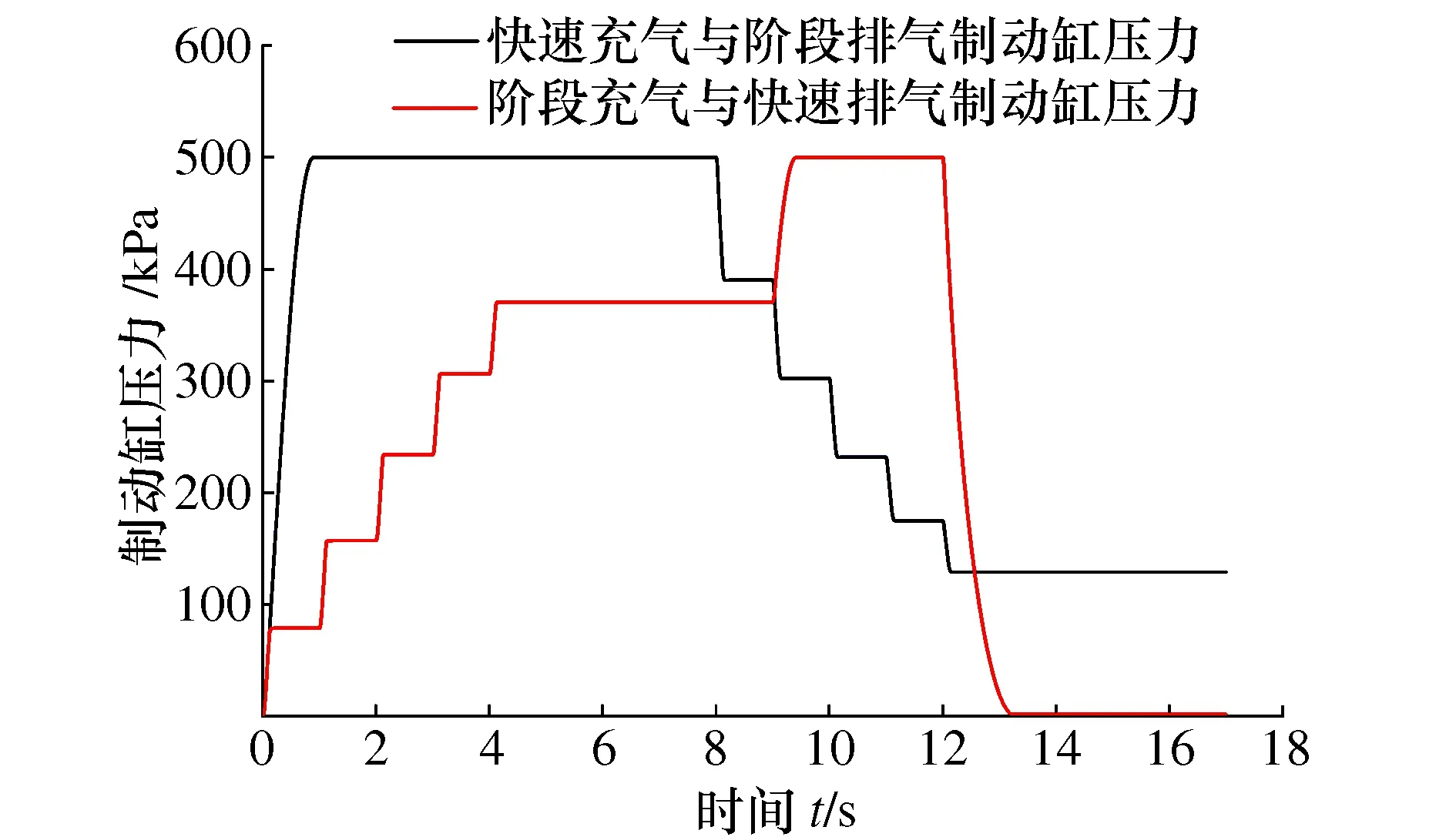
图4 充排气性能测试结果Fig.4 Test results on charging and exhaust performance

由图4中黑色曲线(快速充气与阶段排气制动缸压力)可知,制动缸压力值从0升至450 kPa所用时间为0.66 s,阶段排气5次并保压4 s后制动缸压力值为129 kPa。由图4红色曲线(阶段充气与快速排气制动缸压力)可知,阶段充气5次并保压3 s后制动缸压力值为370 kPa,快速排气1.2 s并保压3 s后制动缸的压力值为1.66 kPa。仿真结果满足文献[3]中给出的指标要求,验证了防滑阀模型的正确性,为搭建空气制动单元提供支撑。

3 防滑控制系统建模与有效性验证

为了有效模拟轨道列车制动防滑性能,国际标准EN 15595规定,可根据轮轨间不同黏着特性,建立四轴车辆制动防滑控制模型进行制动防滑控制模拟;通过仿真与试验的制动距离、车速及滑动量的结果对比进行制动防滑控制模型的有效性验证。

3.1 制动防滑控制系统建模

按照上述防滑阀建模方法,依次建立电空转换阀、中继阀及紧急阀等阀类数值模型,基于MATLAB/Simulink搭建了空气制动单元仿真模型及四轴车辆制动动力学单元,并利用Stateflow建立了制动防滑控制单元;文献[14]的方法,构建了单节车制动防滑控制系统数值仿真平台,如图5所示。其中,为了更好的模拟轨道车辆防滑控制时的低黏着状态,基于低黏着制动时发生的黏着改善现象,本文采用了Polach黏着理论改进后的低黏着模型[15]。基于MATLAB/Simulink搭建的四轴车辆制动防滑控制数值仿真模型如图6所示。

图5 四轴车辆制动防滑控制数值仿真平台Fig.5 Numerical simulation platform for four-axle vehicle braking and anti-skid control

3.2 有效性验证

根据标准EN 15595,可依次比较制动距离、车速及滑动量的仿真值与试验值,验证四轴车辆制动防滑控制数值模型的有效性。实车试验数据为某型轨道车辆制动防滑专项试验数据,试验工况为制动初速度100 km/h,制动级位为紧急制动,模拟轨面低黏着状态;基于制动防滑控制数值模型按照试验工况进行了模拟。

3.2.1 制动距离

为了对制动距离仿真结果进行验证,标准EN 15595规定制动距离仿真值Ssim与试验值Sreal之间的误差应小于5%,误差计算公式如下

(14)

列车制动性能参数仿真值与实车试验值对比结果如表2所示。其中,列车制动距离仿真值为713.42 m,试验值为712.09 m,两者误差为0.19%,满足标准EN 15595中相关要求。

3.2.2 车速

根据EN 15595标准,在制动开始(制动指令发出瞬间)到列车速度降到15 km/h的时间段内,任一时间点所对应的列车速度仿真值与试验值之间的差值绝对值应小于3 km/h。图7中仿真车速与试验车速曲线吻合较好,并由图中两车速之间的差值曲线可知,在任一时刻的速度差值绝对值均小于3 km/h,满足EN 15595标准中相关要求。

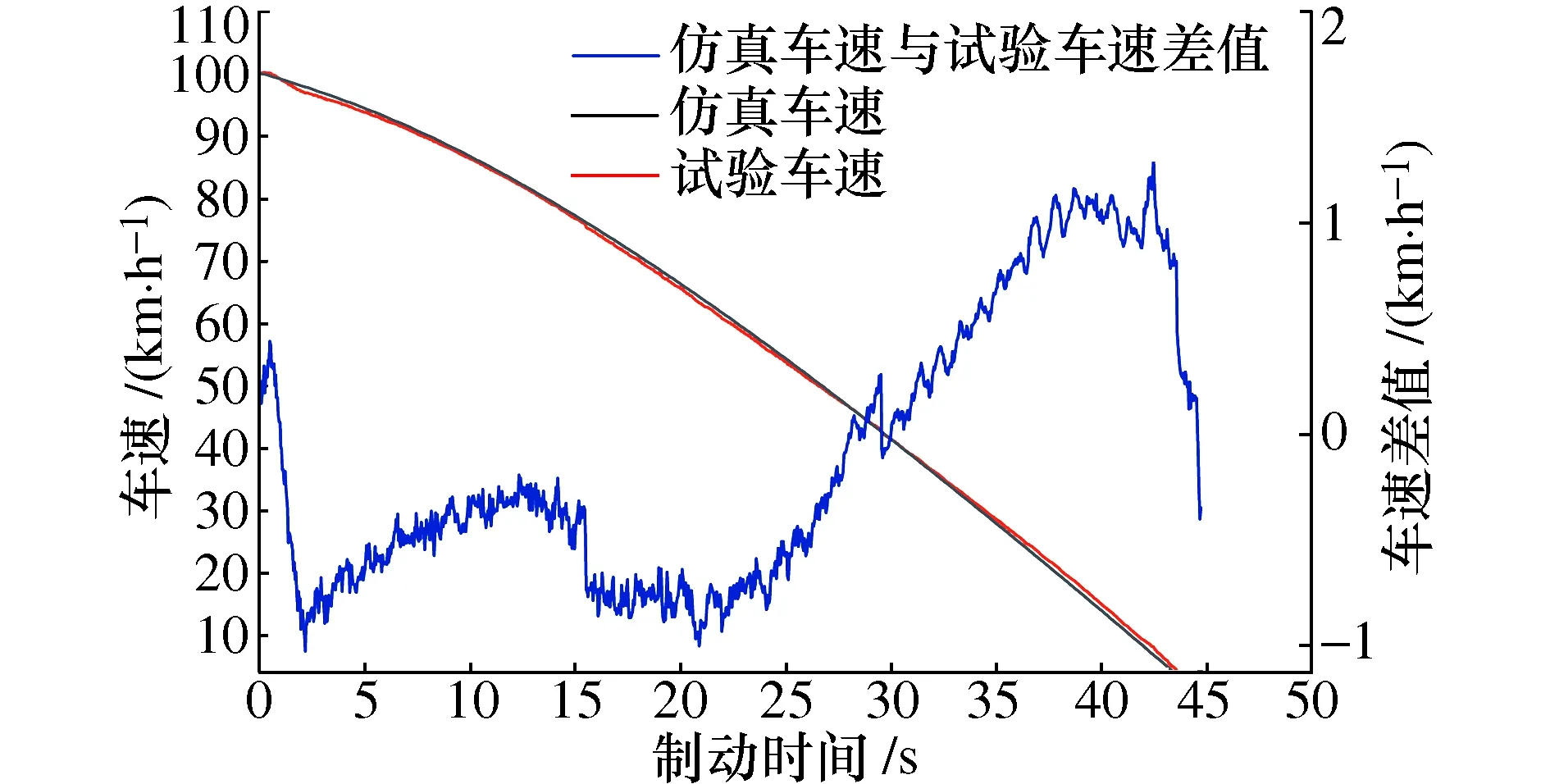
图7 列车速度仿真值、试验值及其差值曲线Fig.7 Train speed simulation value and test value and their difference curves

由图7可知,列车仿真速度与试验速度曲线基本一致,但仍需进行各轴轴速的仿真值与试验值对比。

3.2.3 滑动量验证

图8为每根轴的仿真轴速与实车试验轴速曲线对比,可以看出,两者之间并不完全吻合。按照标准EN 15595中的方法,可以通过滑动量验证对仿真轴速和试验轴速进行比较。

图8 各轴轴速仿真值与试验值对比Fig.8 Comparison between the simulation value and the test value of each axle speed

标准规定,可使用滑移率S定义各轴的滑动间隔,根据各轴在各个滑动间隔内滑动时间所占总时间的比例分别计算仿真和试验的滑动量AS,并进一步计算各轴在每个间隔内的仿真与试验滑动量误差,要求每个间隔内所有轴的滑动量误差总和平均值不大于20%。滑移率S由列车车速及轴速得到

(15)

式中:v为车速;vω为轴速。

滑动间隔定义为: 0≤S<5%,5%≤S<10%,10%≤

S<20%,20%≤S<30%,30%≤S<40%,S>50%。

对于每根轴的实车试验滑动量和仿真滑动量可得:

(16)

(17)

式中:n为轴的编号,本文中取值范围为1～4。计算上述定义的每个滑动间隔中的滑动量误差总和平均值,表达式为

(18)

不同滑动间隔下的仿真与试验滑动量误差结果如表3所示。

表3 不同滑动间隔下的仿真与试验滑动量总和误差结果Tab. 3 Error results of the sum of simulation and test sliding momentum at different sliding intervals

由表3可知,滑动间隔:0≤S<5%内的滑动量误差总和平均值为19.19%,5%≤S<10%内的滑动量误差总和平均值为18.96%,10%≤S<20%内的滑动量误差总和平均值为17.82%,20%≤S<30%内的滑动量误差总和平均值为16.73%,均小于20%;满足标准EN 15595中相关要求。

通过四轴车辆制动防滑控制数值仿真平台得到的制动距离仿真值与试验值的误差符合要求;车速仿真曲线和试验曲线吻合较好,二者任意时刻的差值满足规定;各轴轴速的仿真曲线和试验曲线虽并不完全吻合,但满足标准规定的滑动量验证指标。由此可见,以上结果验证了制动防滑控制数值仿真模型的有效性,且本文所搭建的制动防滑控制数值模型能有效模拟低黏着制动防滑过程。

4 结论

1) 基于轨道车辆常用的三位式防滑阀工作原理,建立了数学模型,利用MATLAB/Simulink搭建其仿真模型,通过对比充排气性能指标验证了该模型的正确性,为空气制动单元的建模提供支撑;

2) 利用四轴车辆制动防滑控制数值模型进行了仿真,制动距离、车速和轴速滑动量误差平均值仿真结果与试验数据的对比验证均满足标准EN 15595中的指标要求,验证方法也可为制动防滑控制理论仿真模型的验证以及半实物仿真模型的验证提供参考。

3) 本文建立的制动防滑控制仿真模型能够很好地再现制动工况下轮轨间的黏着状态,有效地模拟低黏着工况下的制动防滑过程,后续可用于半实物仿真平台搭建,进一步开发和优化制动防滑控制策略。