非高斯随机路面下八轮重型车辆悬架的减振控制方法研究

韩祎,董龙雷,唐攀涛

(西安交通大学 航天航空学院 机械结构及强度国家重点实验室,西安 710049)

随着战场环境需求的提高,对军用装甲车辆这类装备的技术指标也随之提高。大威力、高机动性的军用装甲车辆得到各军事大国的青睐,成为军用装甲车辆装备的主流。装甲车常在山地、沙漠、泥滩等复杂、险峻的路况下行驶,路面不平顺所激发的振动会显著降低车辆行驶的平顺以及机动性能,导致车辆的作战目标无法实现。因此装甲车辆的减振问题一直是国内外学者研究的热点和难点。

建立装甲车辆的整车模型是对其进行减振研究的基础。无论是分析振动对整车性能的影响,还是不同隔振方法与控制策略对车辆的减振效果,都需要考虑车辆的动力学特性,建立整车动力学模型[1]。本文的研究目标为某型号八轮重型装甲车辆,结构庞大,零部件多,是一种非常复杂的非线性多自由度振动系统[2]。现阶段,有部分国内外学者针对装甲车辆及复杂悬架系统进行动力学建模研究。华中科技大学的刘玉霞针对轮式装甲车建立了车身复杂壳体结构的柔体模型,以及悬架系统、动力装置减振系统等主要子系统的参数化振动模型,该模型主要用于对被动悬架的结构参数进行优化[3]。陈花玲等以四轮装甲车为研究目标建立了七自由度整车悬架模型,该模型用于磁流变阻尼器在装甲车辆中的控制研究[4]。刘非以六轮履带式装甲车为研究目标,分别针对扭杆悬挂装置、半主动悬挂装置以及混合悬挂装置建立了半车悬挂模型,并通过Simulink仿真来判断不同悬架的减振效果[5]。刘振旺建立了高速列车的横向运动动力学模型,在模型中纳入了横向半主动控制力,同时耦合了轨道不平顺激励,从而构成了基于轨道不平顺输入的半主动悬挂车辆动力学系统[6]。

综上所述,要准确研究振动控制效果,需针对特定的研究目标八轮重型装甲车辆建立准确的整车悬架模型,并将控制阻尼力与所需控制的自由度纳入模型中。而现阶段,针对八轮装甲车辆如此复杂的动力学系统,整车的悬架模型建立较少,多数研究集中在四轮整车及四分之一悬架模型的建立。因此,本文首先针对研究的某型号八轮重型装甲车,结合其所用磁流变半主动阻尼器,建立精确的整车模型,为其控制研究做准备。

除了整车悬架模型的建立,对于所行驶随机路面的准确表征也是减振控制中存在的难点。现阶段,在研究车辆振动过程中用到的随机信号基本都是通过傅里叶变换,将现场测试数据转换为频域信号[7-13],在此基础上利用功率谱密度函数仿真生成。由于随机路面数据的功率谱表示(即振动能量在相关频率间隔内的分布)可以清楚地揭示测量所得振动的频率分布,帮助避免危险的共振现象[14],因此被广泛应用。然而,学者们忽略了具有相同功率谱密度的随机信号之间的差别。换言之,该方法使得功率谱密度函数能够表征的特性之外的振动性能消失,其中最主要的为非高斯特性[15]。当车辆在道路上行驶时,测量得到的数据中会出现少量超过平均振动水平的高峰,例如路面坑洞就是导致该极端情况出现的原因之一。即使是一眼看去很平坦的道路,也有较为粗糙的路段。而高斯随机信号整体趋于平稳,在对实际路面起伏特性的表征中存在误差,且装甲车辆行驶的路面较普通车辆更加崎岖。因此,为更好地对装甲车辆进行减振控制,实现对路面非高斯特性的准确表征至关重要。

1 整车半主动悬架模型的建立

图1所示为本文所研究八轮重型车辆的整体坐标系。坐标系原点位于车辆质心,x与y轴都平行于地面,x轴指向车辆运动前方,y轴指向驾驶员左侧,z轴垂直于地面指向上方。

图1 车辆运动坐标系Fig.1 Vehicle motion coordinate system

在图1 中指定的整车坐标系基础上,建立整车悬架模型。图2 所示为八轮重型装甲车的半主动悬架结构。在悬架模型的建立过程中,考虑车辆的垂直运动、俯仰运动、侧倾运动3个自由度,根据整车动力学平衡原理,可分别得到车辆的垂直、俯仰、侧倾运动方程。

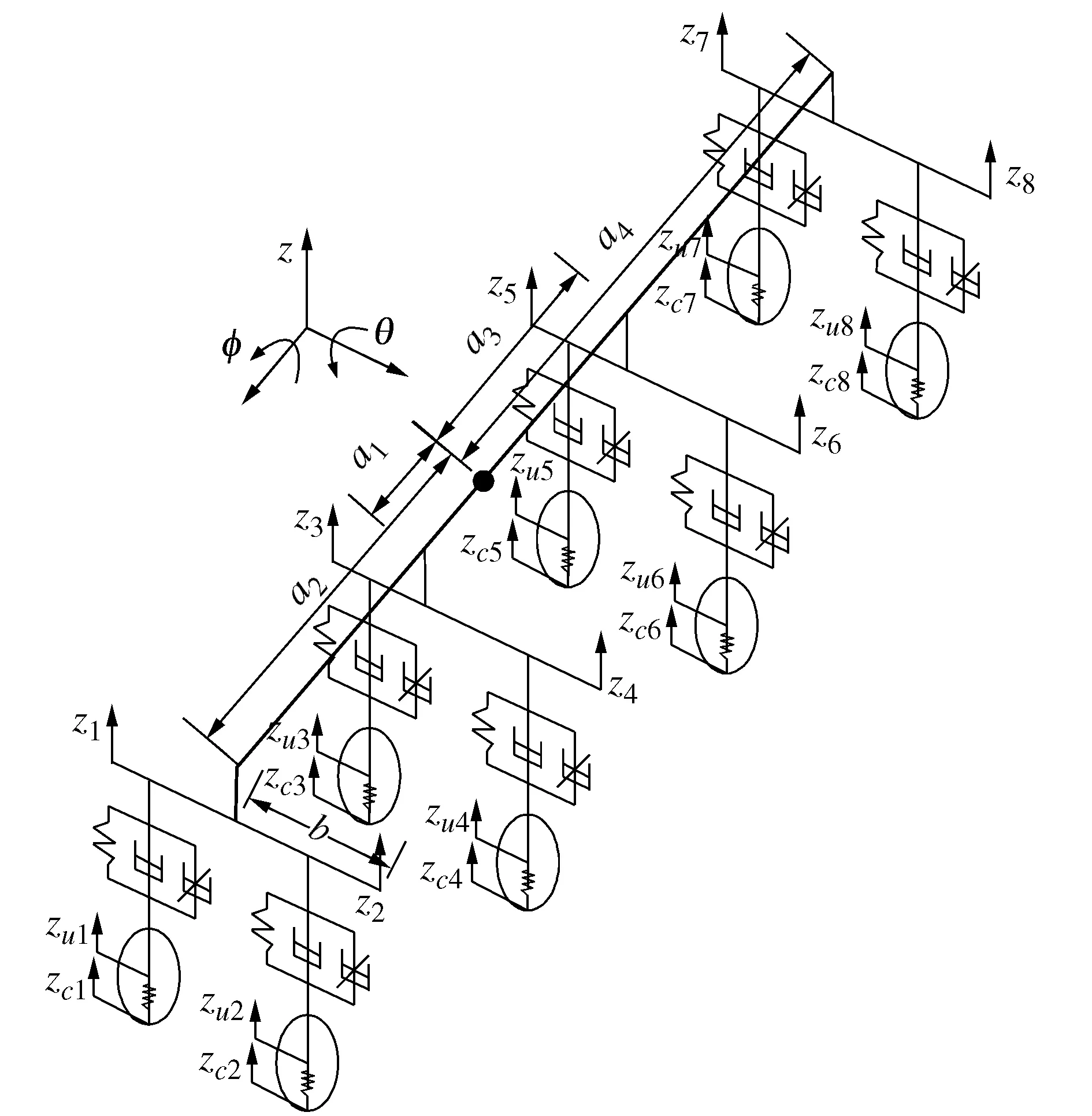
图2 八轮重型车辆整车悬架模型Fig.2 Whole vehicle suspension model of eight wheeled heavy armored vehicle

车辆垂直运动方程为

(1)

车辆俯仰运动方程为

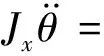
(2)

车辆侧倾运动方程为

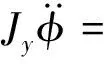
(3)

单个阻尼器平衡方程为:

(4)

由于车身的侧倾角φ、俯仰角θ较小,因此以下关系的成立并不会导致较大的误差产生。

(5)

车辆的俯仰、侧倾与垂直运动之间存在如下关系:

(6)

式(1)～(6)中:ms为车辆簧载质量;z为车辆质心处的垂直位移;φ为车辆质心处的侧倾角;θ为车辆质心处的俯仰角;c为悬架阻尼系数;k为悬架刚度;kc为轮胎刚度;a1,a2,a3,a4分别为车辆质心到第二排、第一排、第三排、第四排车轮轴的距离;b为各排车轮轴轮距的1/2;Jx为车辆俯仰转动惯量;Jy为车辆侧倾转动惯量;zci为地面传递给每个轮胎的垂直位移,i取值为1,2时分别代表第一排的左右两车轮,同理取值3～8时依次代表第二、三、四排的左右两车轮(以下包含i的变量中,i的取值所代表意义相同);zui为各悬架非簧载质量垂直位移;zi为各悬架簧载质量垂直位移;mui为各悬架的非簧载质量;Fmri为各磁流变阻尼器悬架提供的可控阻尼力。

针对所研究的八轮装甲车结构,建立了考虑车辆垂向振动,俯仰运动,侧倾运动的整车悬架模型,并利用MATLAB/Simulink进行系统仿真,为控制研究打下基础。

2 非高斯时域信号

2.1 高斯信号在随机路面表征时的误差分析

图3所示为实验测试得到的车辆在随机路面行驶时的加速度时域信号。针对测量数据,利用功率谱密度方法,仿真得到模拟加速度时域信号,该方法得到的信号为高斯信号,如图4所示。

图3 非高斯载荷信号Fig.3 Non-Gaussian load signal

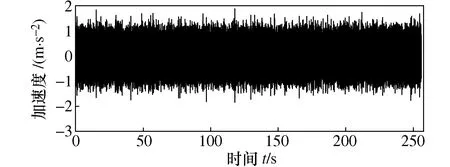
图4 高斯载荷信号Fig.4 Gaussian load signal

图5所示为实测信号与模拟信号的功率谱密度对比。从图5中可看出,二者的功率谱密度非常接近。当车辆在道路上行驶时,测量得到的数据中会出现少量超过平均振动水平的高峰,从图3中可以看到存在这样的高峰值,但在图4所示的模拟信号中不存在该高峰。图3与图4所给出的时域信号之间的差别,非常简洁明了地表征了功率谱密度函数法生成的高斯随机信号在对随机路面进行表征时存在的误差程度。很明显,这两种激励对车辆结构、乘坐舒适性以及电子设备可靠性的影响将大不相同。

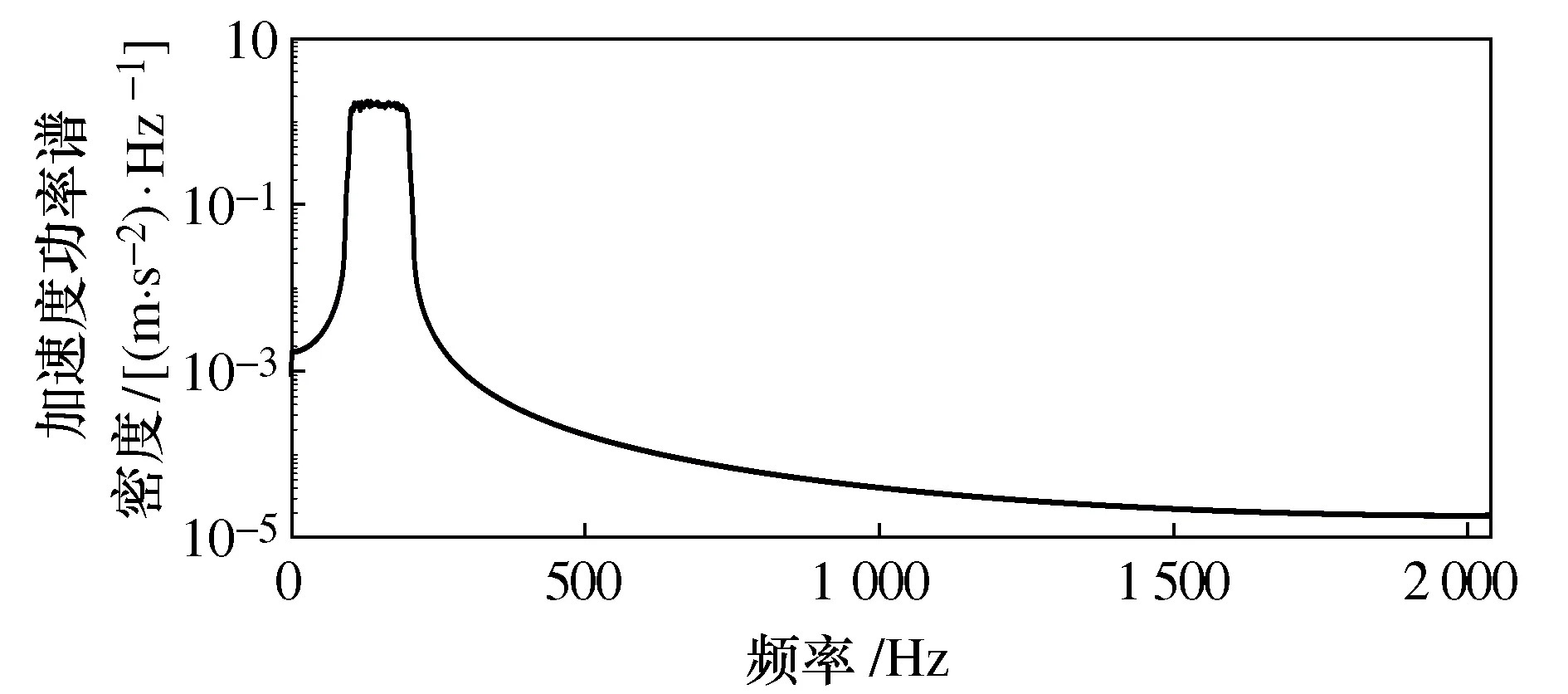
图5 功率谱密度Fig.5 Power spectral density

图6 振幅概率密度分布Fig.6 Amplitude probability density distribution

2.2 非高斯信号的定义

如果随机变量x的概率密度函数p(x)如式(7)所示,则称其为高斯变量。

(7)

式中:μ为平均值;σ为标准偏差;二者分别是振幅概率密度函数的第一与第二中心变量。

(8)

(9)

(10)

对于离散时间序列,平均值μ与第j阶矩Mj被定义为:

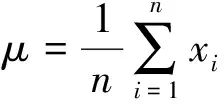
(11)

(12)

式中n为实验中记录的点数。给定类型的变量分布自由度,对其进行完整描述所需的中心矩阶数定义。例如,对于高斯分布,只需平均值μ与方差σ2两个中心矩,足以完整定义振幅概率密度函数的形状。因此,高斯分布具有两个自由度。

峰度ku与偏度sk是描述非高斯振幅概率密度函数的两个主要指标。可根据中心力矩表示为:

(13)

(14)

峰度值表示振幅概率密度函数峰值的锐度和尾部的宽度,偏度值则是振幅概率密度函数不对称性的度量。激励信号的峰度和偏度值都会影响车辆的行驶平顺性,但峰度值对行驶平顺性的影响远高于偏度,因此在减振控制时,主要关注激励和应力响应的峰度值。将峰度值ku=3的信号定义为高斯信号,当峰度值ku≠3时,则信号为非高斯信号[16],如果ku>3,则该过程被视为尖峰态,如果ku<3,被视为低峰态。当路面激励处于尖峰态时,会导致车体发生更加剧烈的振动。而实际的随机路面尤其是崎岖路面,多数属于尖峰态的非高斯随机信号,因此,在车辆减振控制的研究中考虑路面的非高斯特征非常重要。

2.3 非高斯信号的生成

根据非高斯信号的定义,利用功率谱密度生成随机信号,信号频率范围为5～40 Hz,相位服从[0,2π]的均匀分布。利用非线性变换,设定信号的峰度值为10,得到非高斯信号x(t),采样率为4 096 Hz,如图7所示。

图7 非高斯随机路面信号Fig.7 Non-Gaussian random road signal

3 半主动悬架控制器的设计

针对高斯随机路面和非高斯随机路面两种工况,设计与调节磁流变阻尼器半主动悬架控制器,尽可能使悬架系统最大程度发挥其减振性能,保持装甲车辆在崎岖险峻工况下的行驶稳定性。磁流变阻尼器的控制是通过对输入电流的控制实现的。磁流变半主动悬架控制系统如图8所示,为本文的整体控制思路。悬架系统受到路面激励时,簧上、簧下质量会产生垂直振动。以簧上质量振动速度,簧上、簧下质量振动速度之差作为状态变量,输入到系统控制器,得到相应的期望阻尼力。将所得期望阻尼力值输入到所建通用逆模型中,得到控制电流值,并将其输入磁流变阻尼器对车辆振动进行控制。

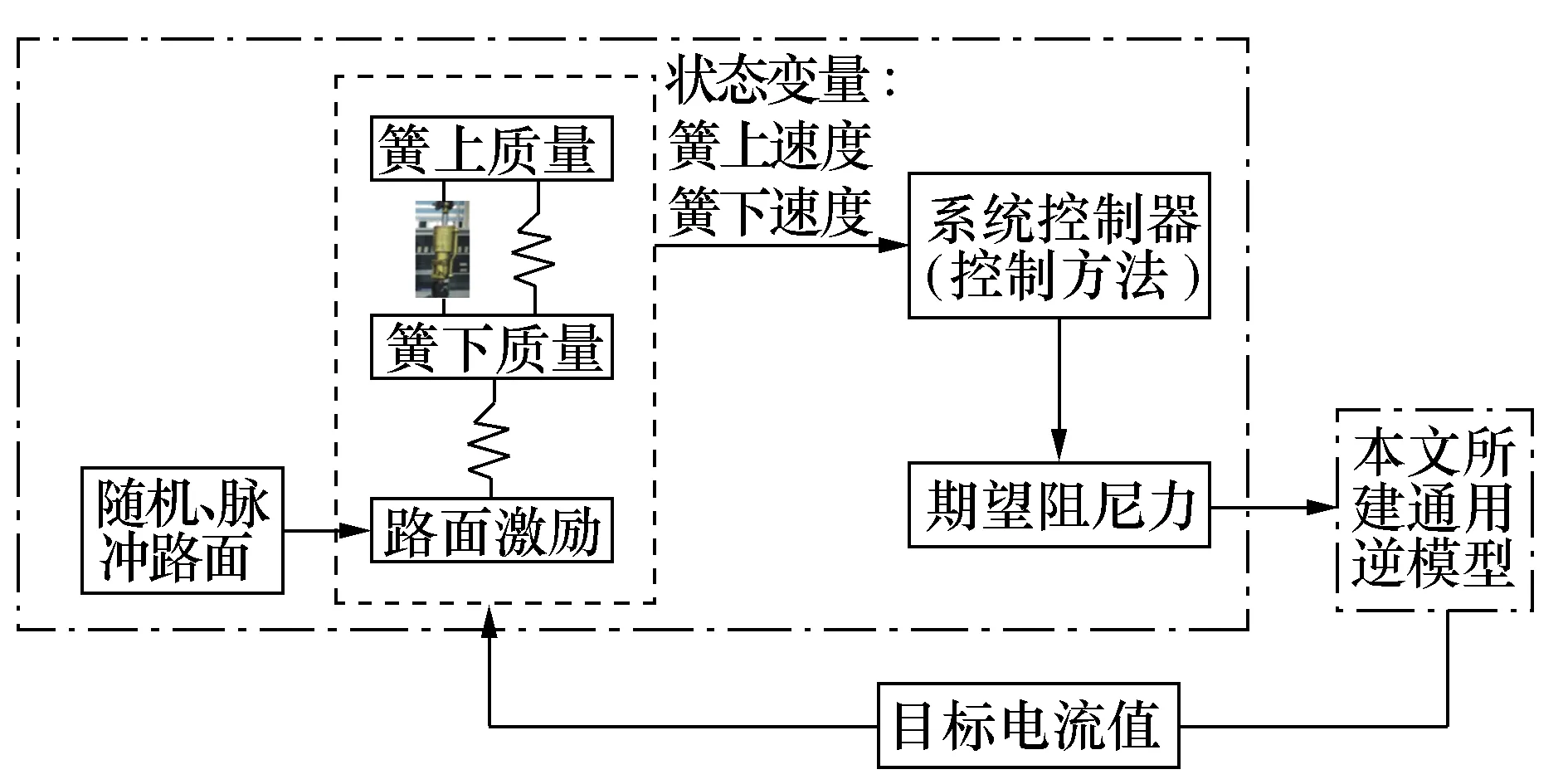
图8 磁流变半主动悬架控制系统框图Fig.8 Block diagram of magnetorheological semi-active suspension control system

3.1 控制算法

控制算法的选择是整个控制过程的核心。关于磁流变阻尼器悬架的控制研究很多,从传统的天棚控制、PID控制,到近些年来被广泛研究的深度学习、强化学习等控制方法,都被应用于磁流变阻尼器悬架的控制。由于磁流变阻尼器电流在0～3 A之间变化,变化范围较小,且传感器测得的车辆振动变量与期望阻尼力的对应关系是固定的,不需要复杂的控制方法,且在上文的研究中已经对磁流变阻尼器的动力学模型进行了准确的建立。因此,本文选择传统的天棚、模糊控制方法与所建通用逆模型相结合,对磁流变阻尼器进行控制。

1) 天棚控制策略

图9所示为天棚控制策略的理想模型。

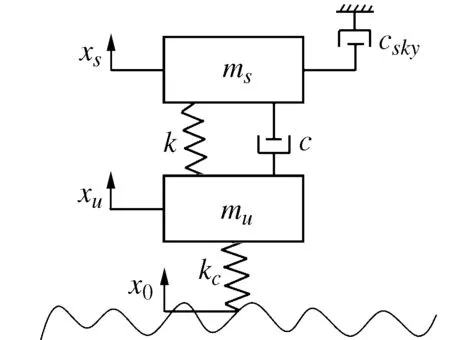
图9 天棚控制策略理想模型Fig.9 Ideal model of sky-hook control strategy

根据图9可得理想天棚控制策略的动力学方程:

式中:x0为路面输入轮胎的位移;xu为簧下质量位移;xs为簧载质量位移;mu、ms分别为簧下质量、簧载质量;k、c、kc分别为悬架刚度、悬架阻尼系数、轮胎刚度;csky为天棚阻尼系数,天棚阻尼控制策略主要通过调节的csky值,对阻尼器的减振效果进行调节。

2) 模糊控制策略

传统的控制方法需掌握被控对象的精确动态信息,才可实现对被控对象的准确控制。针对悬架系统这类复杂非线性系统,准确地根据某一时刻的动态信息预测得到期望阻尼力存在困难。因此,提出了模糊控制方法,该方法存在以下优点:

① 模糊控制是一种依赖人类经验的语言规则控制,无需建立准确的数学模型,并可根据控制效果进行调试,简洁方便;

② 模糊控制方法鲁棒性较强,相较一些传统的控制方法,工况以及参数的改变对控制效果影响较小。更加适用于非线性、时变及迟滞系统;

③ 模糊控制方法与人工控制方法较为接近,对系统的适应性增强。

3.2 控制效果

1) 高斯随机路面

在路面输入为高斯随机路面的工况下,分别利用被动控制、天棚控制以及模糊控制3种控制方法,对各悬架进行控制。并且根据所建整车Simulink模型,考察车辆质心处的垂直振动。如图10和图11所示为高斯随机路面激励下,使用不同控制策略对悬架进行控制时,车辆的振动曲线。如表1所示,为车辆质心处振动速度、位移的均方根(RMS)值,通过均方根值的对比,可以更加直观地评价不同控制方法的减振效果。

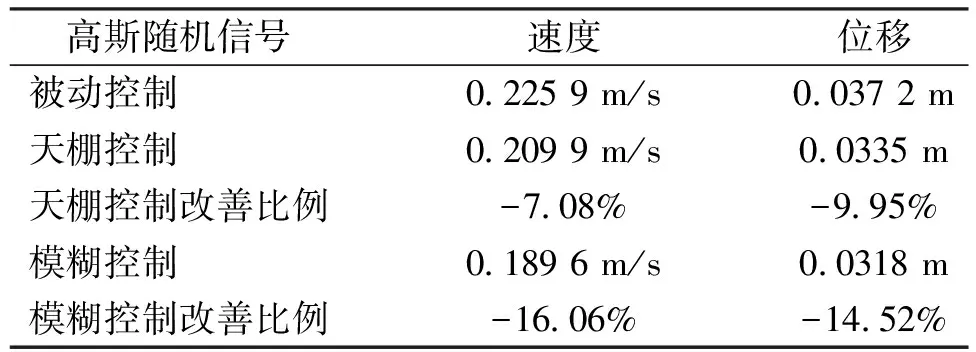
表1 高斯随机路面不同控制策略效果比较Tab.1 Comparison of effects of different control strategies on Gaussian random road surface

图11 高斯随机路面激励下车辆质心处振动位移Fig.11 Vibration displacement at the center of mass of a vehicle under Gaussian random road excitation

通过图10、图11和表1可看出,天棚控制与模糊控制半主动悬架的减振效果优于被动悬架。其中,模糊控制半主动悬架减振效果最优,垂直振动速度降低了16.06%,位移降低了14.52%,减振效果可满足使用要求。

2) 非高斯随机路面

在非高斯随机路面的工况下,同样采用被动控制、天棚控制、模糊控制3种方法对悬架进行控制,并考察车辆质心处的振动。如图12和图13所示,天棚控制与模糊控制等半主动控制方法对非高斯工况下车辆的减振效果并不理想。

图12 非高斯随机路面激励下车辆质心处振动速度Fig.12 Vibration velocity at the center of mass of a vehicle under non-Gaussian random road excitation

图13 非高斯随机路面激励下车辆质心处振动位移Fig.13 Vibration displacement at the center of mass of a vehicle under non-Gaussian random road excitation

尤其是模糊控制法,对车辆质心处振动位移及速度的改善比例在5.75%左右,控制效果不能满足使用要求。通过分析得,由于非高斯信号的峰度值较大。相比高斯信号,非高斯信号在不同时刻加速度值变化较为激烈,速度变化范围也较大。而模糊控制方法的模糊规则是针对高斯信号制定的,因此在非高斯工况下,减振效果大幅降低。

为提升悬架在非高斯随机路面下的减振控制效果,本文针对非高斯信号加速度起伏变化大的特点,提出了一种可以根据簧载质量振动加速度对期望阻尼力进行调节的模糊自适应控制方法。通过传感器测量得到的簧载质量振动加速度值,对期望阻尼力进行调节,调节规律如下:

Fdz=λFdm

(16)

(17)

式中:Fdz为模糊自适应控制器计算得到期望阻尼力;Fdm为模糊控制器计算得到的期望阻尼力;λ为自适应修正系数;γ为自适应控制比例因子,0≤γ<1,自适应方法只改变原有模糊控制器计算得到的期望阻尼力取值,不改变其方向。

模糊自适应控制原理为:若簧载质量的振动加速度与速度同向,则证明此时簧载质量的振动速度仍然在继续增加,通过自适应方法,增大阻尼力的值,加速对簧载质量振动的抑制。若振动加速度与速度反向,则说明此时簧载质量的振动速度在减小,此时根据加速度值适当减小期望阻尼力。

(18)

表2 非高斯随机路面不同控制策略效果比较Tab.2 Comparison of the effects of different control strategies on non-Gaussian random road surfaces

图14 改进后非高斯随机路面激励下车辆质心处振动速度Fig.14 Vibration velocity at the centroid of the vehicle under improved non-Gaussian random road excitation

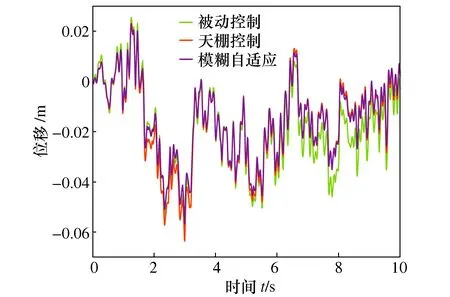
图15 改进后非高斯随机路面激励下车辆质心处振动位移Fig.15 Vibration displacement at the center of mass of the vehicle under improved non-Gaussian random road excitation

4 结论

为实现对八轮装甲车辆的减振控制,建立了复杂的整车悬架动力学模型。在此基础上,对路面的非高斯特性进行研究,并仿真得到非高斯随机路面信号。首次在装甲车辆的减振研究中考虑了随机路面的非高斯特性,该信号更符合装甲车辆的实际运行工况。通过控制策略的研究发现,针对高斯随机路面所制定的模糊控制规则应用于非高斯路面时,控制效果欠佳。为实现快速、精准的控制,对模糊控制方法进行改进,针对非高斯工况下部分点车辆加速度值较大的特点,根据测量得到的振动加速度值对模糊控制方法进行自适应调节。通过验证,所建模糊自适应法可在非高斯路面下实现良好的整车控制效果,且控制效率高,硬件实现简单。