管绞车筒体动力学分析及响应面优化研究

万光海, 王全龙,2, 武美萍,2, 缪小进,2, 韩志平

(1. 江南大学 机械工程学院,江苏无锡 214122;2. 江南大学 江苏省食品先进制造装备技术重点实验室,江苏无锡 214122;3. 法尔胜集团泓昇重工有限公司,江苏江阴 214400)

管绞车作为钢丝绳制造的主要设备,如图1所示,其运转性能对钢丝绳的捻制性能有极大影响,特别是筒体部件,其回转的稳定性直接决定了钢丝绳的疲劳强度和寿命。且筒体的可靠性还直接决定着钢丝绳制造工作效率,也决定着管绞车设备的安全可靠性。受工作环境影响,筒体在高速运转时会产生很大的离心力,同时还受到内部其他零件施加的载荷影响。如果在这种复杂工况下,引起的振动频率与筒体自身的固有频率接近时,筒体易发生大幅度振动,从而破坏整个设备的安全可靠性,影响工作效率和钢丝绳生产质量。故研究管绞车筒体振动问题,探索动力学仿真及优化方法,是提高筒体甚至管绞车可靠性和安全性亟待解决的关键问题。

图1 管绞车实物图Fig. 1 Physical diagram of the pipe winch

机械设备的共振问题是机械装备设计研发不可避免的关键问题,一直受到相关学者的广泛关注。目前,国内外学者主要通过有限元仿真的方法分析结构共振问题,常晋雷[1]研究了矿用气动绞车的模态分析,发现前6阶固有频率相对较高,远离绞车工作频率,且振型主要发生在制动圈上。为验证塔机的稳定性,付石等[2]分析了塔机动力学模态,发现变形主要发生在平衡臂和起重臂。Xia等[3]测试了京广铁路列车作用下东、西、南、北塔的响应和微地震作用,建立数值模型并利用有限元分析,结果发现振动前3阶宝塔的频率相似,其中1阶振动模态是弯曲的,第2和第3阶模态为剪切弯曲,且最大载荷处的振动对宝塔的安全性影响不大。宗荣[4]研究梳棉机锡林机构的模态,并进行了分析和评价,验证了锡林机构中振动的安全性。Zhang等[5]研究了车桥耦合振动对车辆平顺性的影响,基于动平衡原理和有限元方法,分析了多辆车辆通过斜拉桥时不同铺装水平下的车辆动力响应及平顺性。分析结果表明,随着路面平整度的提高,车辆的动力响应减小,车辆的平顺性得到改善,降低了车桥耦合振动响应。

也有些学者针在分析振动问题的基础上,对振动问题提出各种优化。张夏琦等[6]研究了采煤机联结架的动力学分析,发现1阶固有频率对联结架影响较大,易引起共振,并通过增加壁厚来增加固有频率,以此优化结构。白颖等[7]为降低柴油机的振动问题,对机体开展了模态分析和瞬态动力学分析,从振动剧烈部位改进结构,通过实验验证了改进的有效性。房建斌等[8]针对电子设备托架疲劳损坏的问题,研究了托架在约束、构型方面的协同优化,并基于仿真分析验证了托架优化的准确性。Rubio等[9]研究了一种安装在镗杆上的被动动力吸振器(DVA)参数的优化选择,采用了无约束优化问题的经典方法,结果表明,稳定性明显改善。Zhang等[10]对了研究金属镗杆颤振问题,基于AMDM建立了一种锥形复合镗杆的模型,研究发现通过选择合适的锥度比、铺层角、L/ratio和碳基复合材料等,可提高锥形模型的固有频率和颤振稳定性。此外,针对优化设计还有学者采用响应面优化,王欣欣等[11]等为最小化钻孔支撑结构的变形和质量,建立了反映钻孔支撑结构关键尺寸与优化目标之间关系的两目标响应面模型,并采用非支配排序遗传算法(NSGA-II)求解,使结构得到大幅度优化。Wang等[12]等对框架结构特性进行了静力分析和动力分析,基于响应面法找到了在满足许用应力条件下使质量最小的优化方案。米男男和李光[13]研究了缓冲垫的多目标优化设计,以缓冲垫的加速度、最大变形量和包体质量为目标函数,进行响应面优化设计。通过响应面优化分析,提高了封装的性能,获得了高性能、轻量化缓冲垫。由此可见,响应面优化设计在结构性能和轻量化优化方面具有一定优势。

通过开展管绞车筒体动力学分析及优化实现抗振性能提升,首先建立筒体的有限元模型,并对筒体进行模态分析和谐响应分析,分析筒体的固有频率及其与变形和振幅的关系。然后基于灵敏度分析筛选设计变量,通过面心复合设计获得试验设计点,并建立Kriging响应模型对筒体振动性能进行优化,获得性能优异且轻量化的筒体。

1 有限元模型和方法

以管绞车筒体为研究对象,采用Solidworks建模软件建立筒体的三维模型,如图2所示。将该模型以x-t格式保存,并导入到Ansys Workbench中,进行有限元仿真分析。

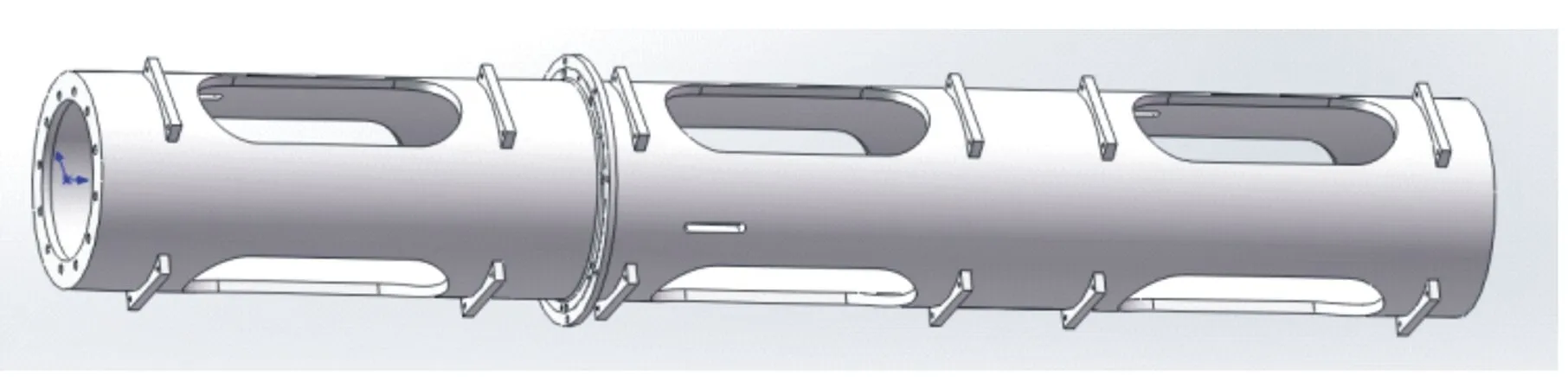
图2 筒体三维模型 Fig. 2 Three-dimensional model of the cylinder

1.1 定义材料属性

根据管绞车实际工作环境及性能要求,设置筒体厚度为16 mm,材料为20#钢,其具体性能参数见表1。

表1 筒体材料的基本性能Tab. 1 Basic properties of cylinder material

1.2 网格划分

网格质量的好坏会直接决定有限元计算的效率和精确性,网格尺寸过大会致使计算精度差,网格尺寸过小又会降低计算效率,因此要根据模型尺寸和计算所需精度来确定网格尺寸。针对多个网格尺寸进行模拟分析,得出网格尺寸大小与模态分析所得频率之间的关系如图3所示。网格尺寸与单元节点的关系如表2所示。

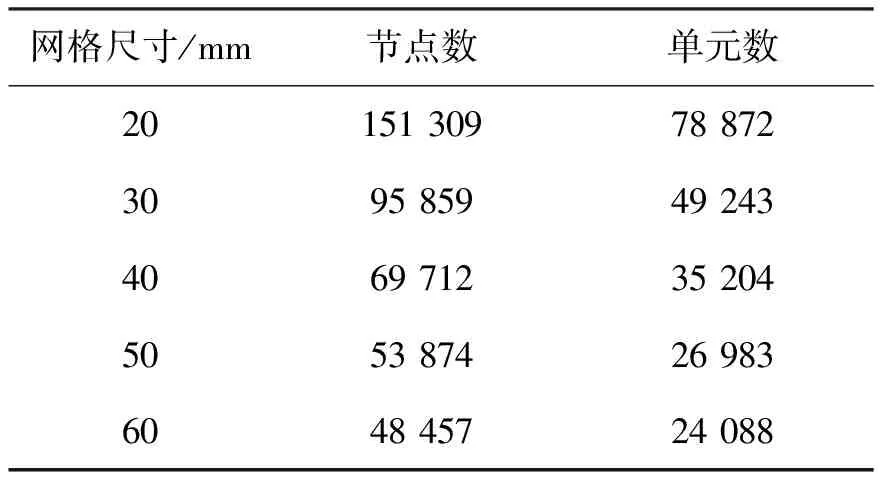
表2 网格尺寸与单元节点的关系Tab. 2 The relationship between mesh size and element nodes

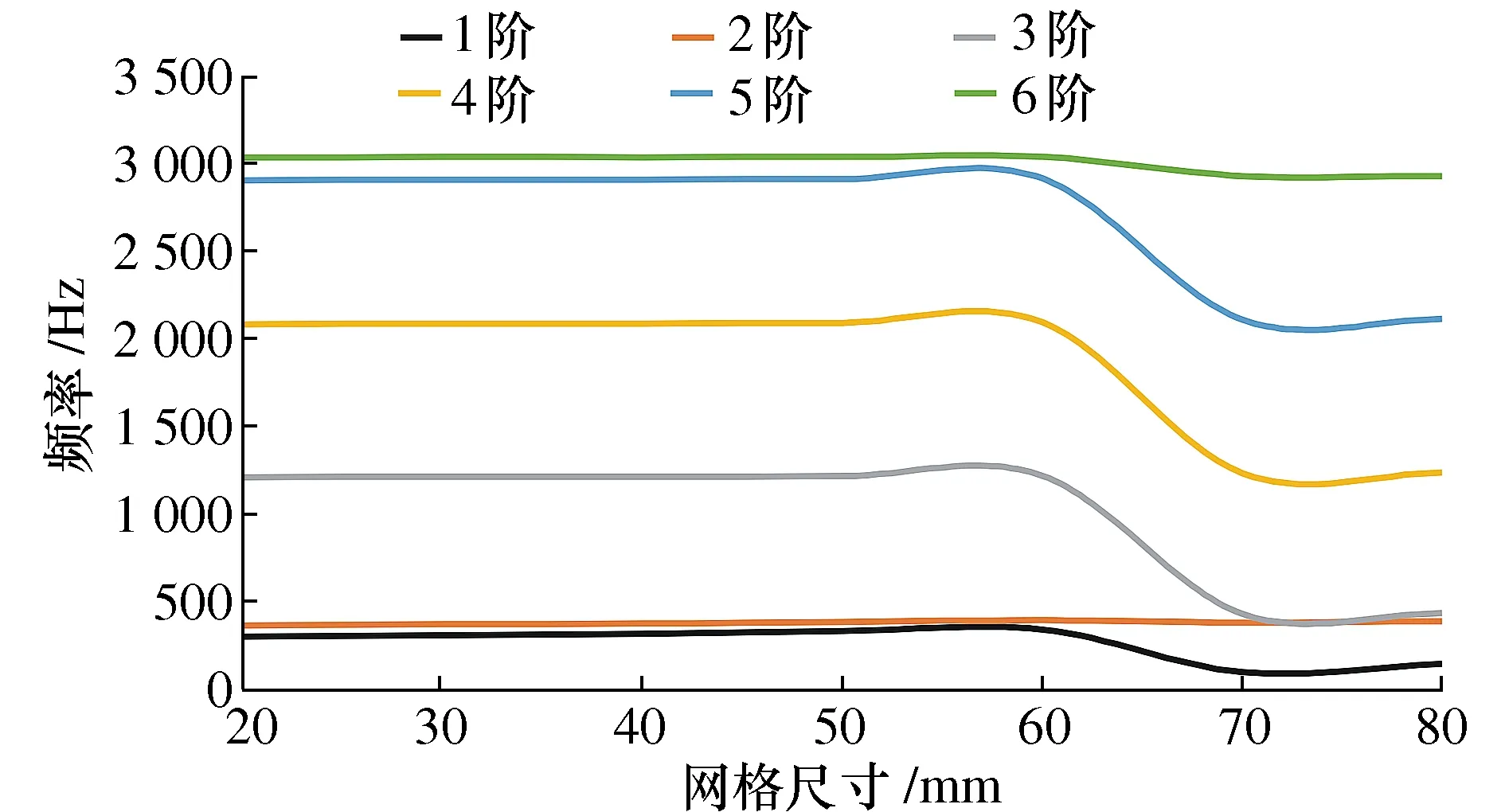
图3 模态分析得到的网格尺寸与频率的关系Fig. 3 Relationship between mesh size and frequency obtained from modal analysis

从图3和表2中可以看出,随着网格尺寸的减小,所得到的各阶频率也在减小,但减小十分缓慢,趋于稳定。同时随着网格尺寸的减小,单元个数和节点数也在不断增加即计算精度在增加,但求解所需时间也在增加。本文在保证计算精度的前提下,选择网格尺寸40 mm来进行网格划分并求解。网格划分后的模型如图4所示,该模型有69 712个节点,35 204个单元,单元类型采用Solid186网格单元。

图4 网格划分模型Fig. 4 Mesh partition model

2 仿真结果及分析

2.1 模态分析

模态分析是动力学分析的基础,用于确定模型结构的固有振动特性,对机体进行约束模态分析可获得机体的固有频率和振型[14]。通过模态分析所得到的固有频率对装备设计中的避免共振具有指导性作用。此外,模态分析的结果可用于其他基于模态叠加法的动力学分析中,如谐响应分析。由牛顿力学理论可得到动力学通用方程,即

(1)

由于常见结构的阻尼比小于10%,对结构固有频率的影响很小,故一般不做考虑。所以模态分析的有限元方程可直接写成

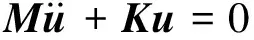
(2)

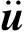
当筒体运转时,发生简谐运动即

u=φisin(ωi+θi)

(3)

与之相对应的加速度向量可以表示为

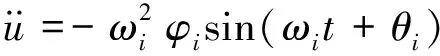
(4)

将式(2)和式(3)代入式(1)中可得到

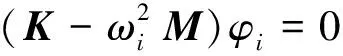
(5)

式中:ωi为结构的第i阶固有频率;φi为结构的第i阶振型向量。

理论上,结构的固有频率有n阶,阶次越高固有频率值也越大。对于低阶固有频率研究更有意义, 因为对于高阶固有频率,自振时间较短,自振周期较低,对结构造成的破坏影响不大[15],而且系统的工作频率或者环境激励频率一般情况下都比较低,因此通常情况下,只需取前几阶固有频率进行研究即可满足要求。三孔筒体前6阶固有频率及变形如表3所示,模态振型如图5所示。

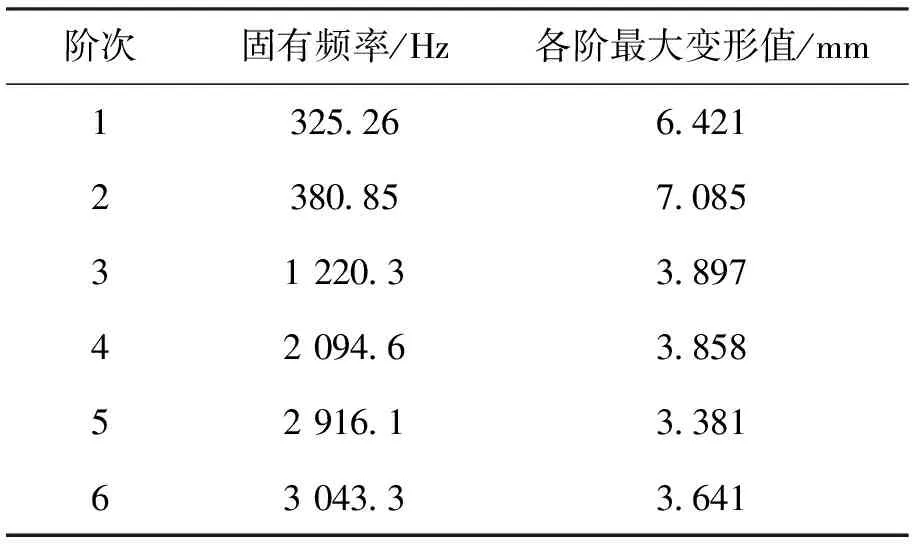
表3 筒体前6阶固有频率及变形Tab. 3 First six-order natural frequencies and deformations of the cylinder

从图5和表3可知固有频率最小为325.26 Hz,最大固有频率为3 043.3 Hz,前两阶固有频率较小,但从第2阶之后固有频率间隔变化较大,尤其第3、第4和第5阶相差较大。此外,第1阶固有频率325.26 Hz以及第2阶固有频率380.85 Hz时,筒体变形最大,分别为6.421 mm和7.085 mm,其他各阶振型相对较小;由此,再结合图5振型可看出筒壁开口处最易发生共振和变形。

2.2 谐响应分析

谐响应分析是用来确定线性结构在已知幅值和频率的正弦载荷作用下的稳态响应。输入载荷一般是力、应力或位移,输出一般是节点位移、应力、应变等。采用谐响应方程分析管绞车筒体在已知载荷作用下的动态响应,其简谐载荷作用下的谐响应方程为

(-ω2M+iωC+K)(u1+iu2)=F1+iF2

(6)

式中:F1+iF2为施加的简谐载荷;u1+iu2为稳态位移响应。

以模态分析为基础,通过模态叠加的方法对管绞车筒体进行谐响应计算分析,得到了X,Y,Z方向上频率和振幅的关系,如图6所示。

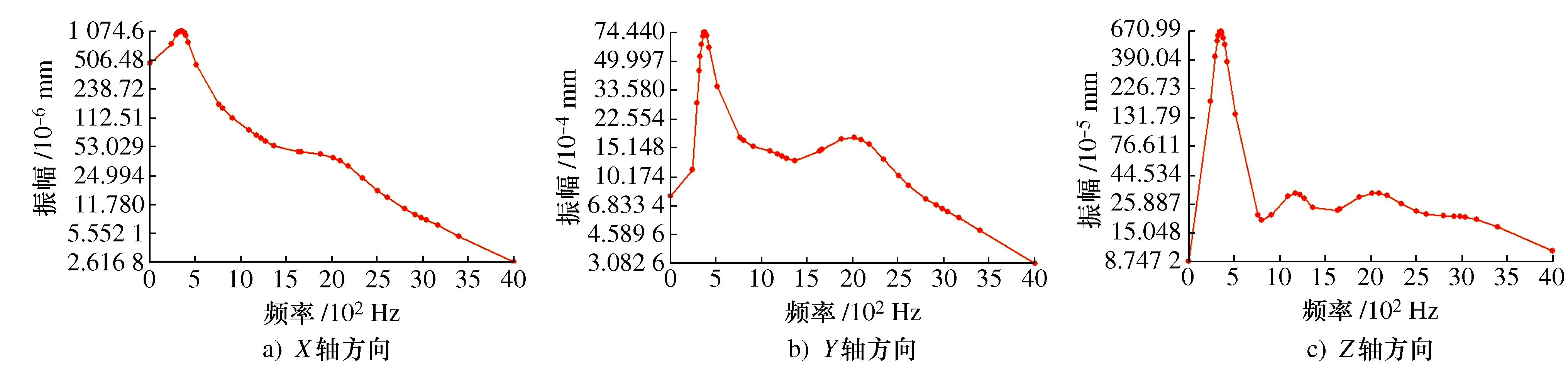
图6 X,Y,Z方向上振幅和频率的关系Fig. 6 Relationship between amplitude and frequency in the X, Y, and Z directions

从图6可以看到,在X轴方向上,频率在338.28 Hz处出现了极值,此时的幅值达到1.074 6×10-3mm;在Y轴方向上,频率也在380.85 Hz处出现极值,幅值达到7.441×10-3mm;在Z轴方向上,频率同样在353.06 Hz处出现了极值,幅值达到6.700 9×10-3mm,且这3个频率分别在模态的第1、2阶固有频率附近。此外,在Y轴方向和Z轴方向上的振幅幅值相比于X轴大得多,故可知筒体在振动极值点处发生弯曲。因此该阶模态固有频率对管绞车筒体的振动有较大影响,易引起共振现象,在设计时应尽可能避免。

3 管绞车筒体动力学优化

3.1 筒体初步结构优化

管绞车筒体原设计从轻量化考虑将筒体每个周向设计三孔,每节筒体共九孔,但依照原设计,筒体固有频率较低,经过前面模态分析和谐响应分析发现易产生共振和变形。现设计两孔筒体,通过对比两孔的模态和振型,探究开孔数量对筒体振动的影响,并以此对筒体进行初步结构优化。原三孔筒体每孔开孔宽度为193.7 mm,为保证开孔总宽度相同,设置两孔筒体每孔开孔宽度为290.6 mm。其变形云图如图7所示。

将两孔筒体和三孔筒体模态频率及变形进行对比如表4所示。

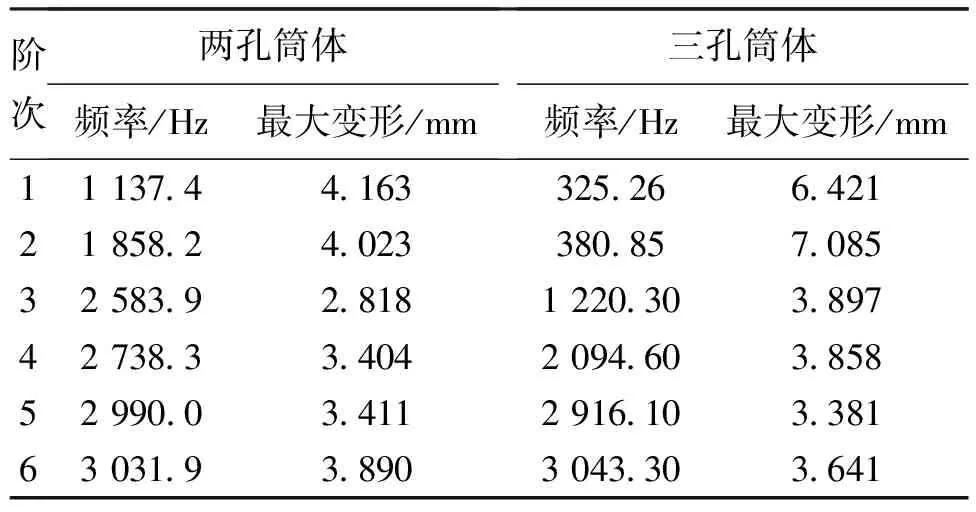
表4 两孔和三孔筒体模态频率及变形对比Tab. 4 Modal frequency and deformation comparison between two-hole and three-hole cylinders

从表4可以看出两孔筒体比三孔筒体的各阶固有频率要高,尤其是前3阶,两孔各阶固有频率的增幅分别达到249%、387%和112%。这表明:外界激励要使筒体共振所需频率更大,即两孔筒体结构要比三孔筒体结构抗振性能更好。此外,在工作中发生共振时,两孔筒体的变形也比三孔筒体变形相对小许多。

此外,从轻量化方面考虑,原设计的三孔筒体质量为368.67 kg,而两孔筒体质量为339.64 kg,质量上降低了7.8%,更加轻量化,以此可见,两孔筒体比三孔筒体抗振和变形方面都更好些。

3.2 模态频率关于筒体参数灵敏度分析

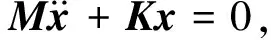
(7)

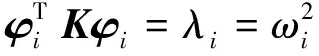
(8)

式中:I为单位矩阵;λi为系统第i阶特征值。

假定第j个影响结构形态的参数为Sj,对式(7)关于Sj进行求导,可得

(9)

基于向量原理,可推导出结构的固有频率对结构参数的灵敏度关系式为

(10)

据上式可知:当结构参数Sj发生变化时,将会直接影响质量矩阵与刚度矩阵的取值,从而导致结构的固有频率发生改变。对于管绞车筒体,可通过优化筒体材料参数以及结构参数来提高筒体结构的固有频率并降低筒体质量,其中材料参数包括弹性模量、泊松比、密度,结构参数包括筒壁厚度(通过筒体内径来体现)和开孔宽度。在优化筒体参数之前,首先探究筒体固有频率和质量相对于筒体各项结构参数的灵敏度。通过灵敏度分析法,揭示结构设计变量对其性能的影响程度,使获取的设计变量更具有针对性,可极大提高结构优化效率。

为此,开展管绞车筒体前两阶模态以及质量关于筒体材料参数和结构尺寸参数的灵敏度研究,以泊松比P1、弹性模量P2、密度P3、筒体内径P4、开孔宽度P5为初选变量,计算筒体质量P6及前两阶固有频率P7和P8关于筒体参数的灵敏度结果如图8所示。

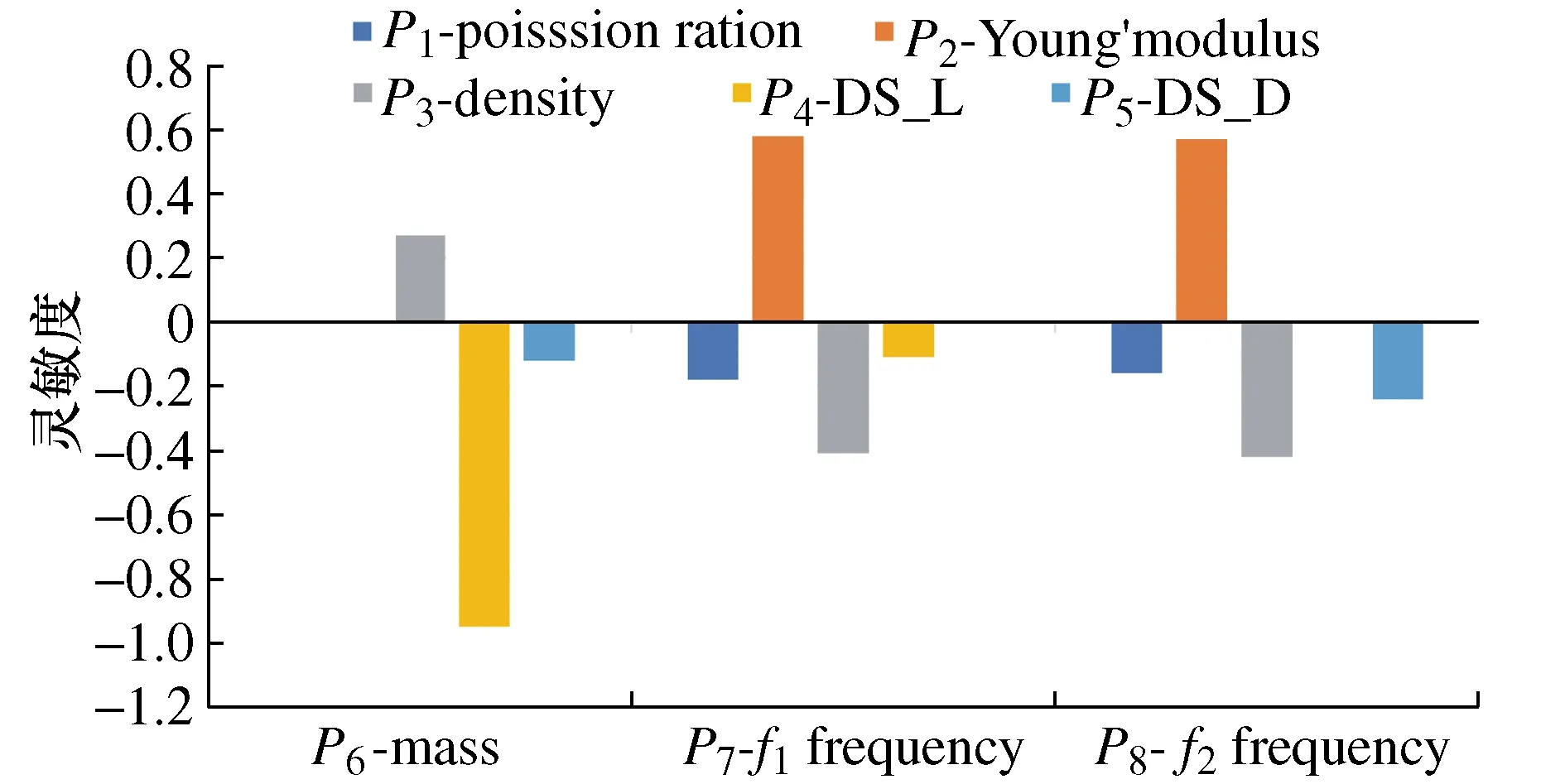
图8 筒体参数灵敏度条形图 Fig. 8 Bar chart of cylinder parameter sensitivity

由图8可知,筒体质量关于筒体内径P4的灵敏度最大,其次是质量密度和筒体开孔宽度,而且P4的灵敏度值为负即呈负相关,这表明随着筒体内径的增加即壁厚的减小,筒体质量P6在减小;而筒体第1阶固有频率P7关于筒体弹性模量P2灵敏度最大且呈正相关而泊松比P1、密度P3、内径P4呈负相关,即表明,随着筒体材料弹性模量的增加,泊松比、密度的减小及壁厚的增加,其第1阶固有频率增加。针对第2阶固有频率P8,各初选设计变量对其影响顺序为:弹性模量>质量密度>开孔宽度>泊松比>内径,其中弹性模量对第2阶固有频率呈正相关,其余呈负相关,即表明筒体材料随着弹性模量增加、其余变量的减小,第2阶固有频率增加。综合看来,泊松比相比其他几个初选变量对这几项输出变量影响最小。故通过以上对筒体质量、前两阶固有频率关于筒体各项参数灵敏度研究,从五个初选变量中选择弹性模量、密度、筒体内径以及开孔宽度这四个灵敏度较高的变量作为优化的设计变量,使其更有针对性,并降低了待优化模型的规模。

3.3 筒体响应面模型

响应面方法是基于统计学和试验设计技术通过DOE点插值或拟合形成的输出变量(筒体质量、第1阶固有频率、第2阶固有频率)关于设计变量(筛选出来的弹性模量、密度、筒体内径以及开孔宽度)的数学函数关系。在可接受的误差范围内,运用构建响应面模型代替筒体有限元模型开展分析和优化,响应面的构建包括设计变量、试验设计和模型构建三部分[16]。

3.3.1 设计变量

考虑到常用金属材料的材料参数范围和筒体结构加工要求,筒体参数设计如表5所示。

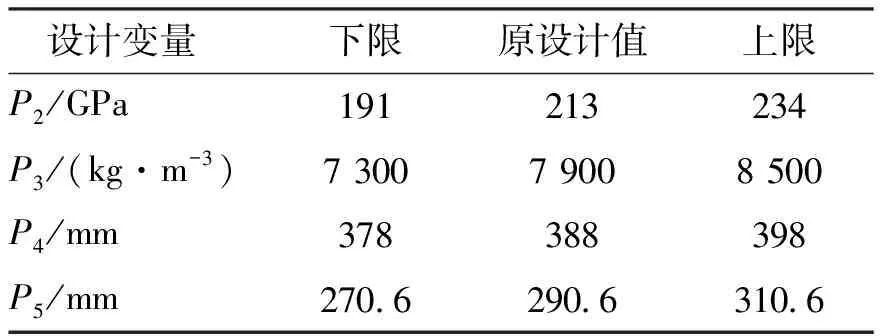
表5 筒体参数设计表Tab. 5 Table for cylinder parameter design

3.3.2 面心复合设计

通过设计一系列样本试验,运用尽量少的资源和计算时间,获得可反映设计目标的高度相关信息数据。试验设计中,好的样本点选取,能降低计算成本又提高响应面精度,所以在设计域内选取一组好的样本点很重要。DOE技术(Design of experiment)是用来拟合响应面的试验样点的选取技术。目前,常用的取点方法的共同之处是用尽量少的样本点对设计空间进行填充,且试验样本点的位置满足一定的对称性和均匀性要求。本DOE取点方法采用面心复合设计,在中心复合设计的基础上,采用Face-Centered填充。面心复合设计的轴点数被设置为±1的水平,是一种三水平试验取样方法,而且面心复合设计在不影响精度的基础上所需样本点数更少,故本文采用该方法获取样本点。求得25组样本点对应的各输出变量结果如表6所示。

表6 面心复合设计试验数据表Tab. 6 Table for the face-centered composite design and experimental data

3.3.3 基于Kriging响应面模型建立

Kriging响应面技术是一种多维插值技术,同时考虑全局和局部的共同影响因素[17]。实际工程问题往往是复杂且非线性的,而Kriging响应面通过所有设计点,拟合度较好,适用于高度非线性的复杂工程优化问题。Kriging响应面拟合既可以解决各向同性以及各向异性问题。同时可避免一次响应面,二次响应面等拟合度较差、且可能陷入局部最优等问题。Kriging模型是空间插值模型,由多项式响应面近似模型和局部偏差结合而成[18],其表达式为

y(x)=F(β,x)+z(x)=fT(x)β+z(x)

(11)

式中:y(x)是待拟合的响应函数;β是基函数回归系数;f(x)是变量x的多项式响应面模型,提供设计空间的全局近似模型;z(x)是期望为0,方差为σ2的高斯随机函数。其协方差矩阵为

cov[z(xi),z(xj)]=σ2R(xi,xj)

(12)

式中R为相关矩阵。选择高斯相关函数

(13)

式中:θk是相关函数参数,用于衡量两样本点之间相关性随两点间的距离增加的衰减度,相关性越小,生成的响应面越光滑;xi,k和xj,k分别是样本点xi和xj的第K个元素。

基于上述Kriging响应面模型理论,根据前面生成的试验设计点,利用Workbench软件中的Response Surface模块,建立Kriging响应面,得到各设计变量对3个输出变量的多个响应面模型。

评价响应面合理性,检验拟合程度常采用R2和RMSE相对均方根误差及相对最大绝对误RMAE等指标。同时,还可在Workbench的响应面模块内查看计算值与预测值关系图,可更直观的判断响应面拟合的合理性和准确性,预测值与计算值的关系曲线越接近于45°的直线,则证明预测的越准确,拟合精度越高。由于采用Kriging模型建立的响应面会通过所有试验点,因此需添加验证点验证响应面模型的准确性。添加验证点后,根据Kriging模型拟合结果和实际计算数值,得到Kriging模型合理性评价指标,如表7所示。

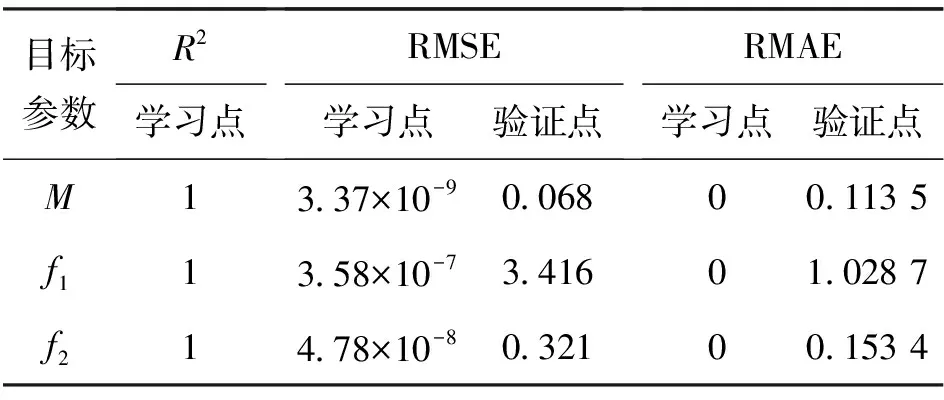
表7 Kriging模型合理性评估Tab. 7 Rational evaluation of the Kriging model

由表7可看出,添加验证点后,验证点处的筒体质量、1阶频率和2阶频率的均方根误差分别为0.068、3.416和0.321,且其相对最大绝对误差分别为0.113 5、1.028 7和0.153 4,拟合度误差在95%以上。从图9更可直观看出,Kriging响应面模型拟合度较高。

图9 Kriging模型计算值和预测值关系Fig. 9 Relationship between calculated and predicted values in the Kriging model

根据所建立的响应面模型,如图10a)材料设计变量以及图10b)尺寸设计变量对第1阶固有频率的响应;如图11a)材料设计变量及图11b)尺寸设计变量对筒体质量的影响。

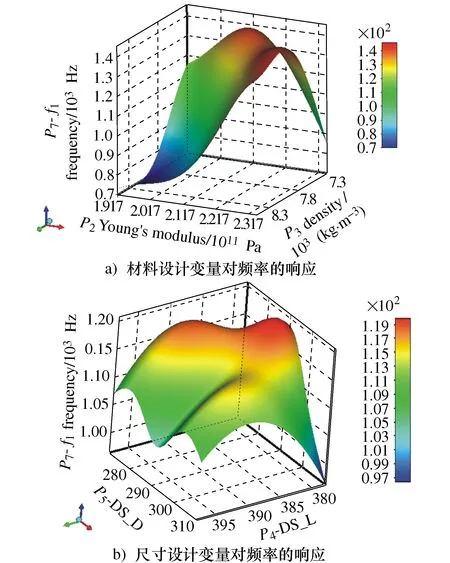
图10 设计变量对频率的响应Fig.10 Response of the design variable to frequency

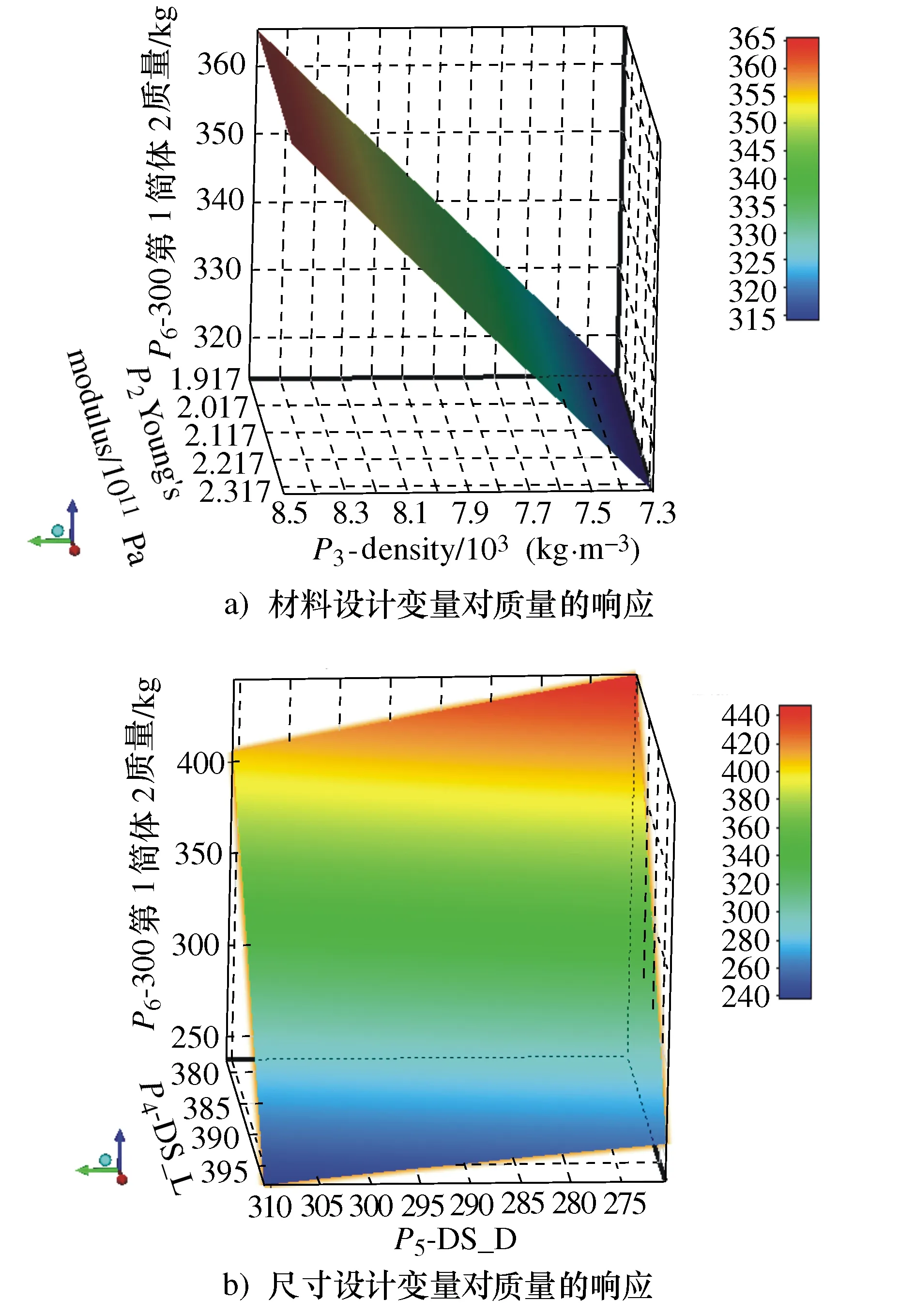
图11 设计变量对质量的响应Fig.11 Response of design variables to quality

从图10a)可看出随着材料设计变量数值的增加,第1阶固有频率存在两个极大值;从图10b)中可发现,随着尺寸设计变量的增加,固有频率先增后减,也存在着极大值。而从图11a)中可以看到随着材料设计变量的增加,筒体质量是呈线性增加的,从图11b)中可发现随着开孔宽度的增加,筒体质量线性递减,而随着筒体内径增加即壁厚的减小,筒体质量在减小。综上,该筒体设计变量将存在一个最优化使固有频率达到极大的同时,又使筒体质量达到最小。

3.4 筒体多目标优化

要实现多目标优化,需先确定本次优化的优化目标和约束函数,本文在实际工况的合理范围内,以前两阶固有频率最大化,筒体质量最小化为优化目标,以筒体材料属性范围、筒体尺寸范围为约束。其优化具体定义如下:

(14)

式中:f1(x)为第1阶固有频率;f2(x)为第2阶固有频率;m(x)为筒体质量;x∈[xL,xU]为设计变量,其中xL为xU分别为设计变量x的下限值和上限值。

建立的优化模型为

minf(P2P3P4P5)=w1×P6

maxf(P2P3P4P5)=w2×P7+w3×P8

(15)

式中:P6、P7和P8均为P2、P3、P4和P5的函数;w(i=1,2,3)为各优化目标所占权重,表达对应目标相对于其他目标的重要性,在Workbench中设置各优化目标重要性分别为default、higher、higher。

采用MOGA方法优化即多优化目标的迭代遗传算法对响应面进行优化,迭代100次,得到3组最优方案,优化方案如表8所示,及结果对比如表9所示。这3种优化方案各项设计变量参数相差很小,其结果也相差不大,其中优化结果最好的是方案2。虽然方案2的质量略高于另外两个方案。但微乎其微,而频率上,1阶频率和2阶频率要明显高于另外两方案。相比于原三孔筒体设计,方案2在质量上从368.67 kg下降到223.77 kg,降低了39%;在频率上,1阶固有频率f1从325.26 Hz上升到940.08 Hz,2阶固有频率f2从380.83 Hz上升到1 750.7 Hz,其增幅分别达到189%和359.7%。此外,在方案2情况下,此时前6阶变形和原三孔筒体对比如表10所示,可以发现前6阶变形在经过优化后,相对于原设计的三孔筒体,其最易发生共振的前两阶变形在一定程度上减小。由此可见,通过多目标优化,不仅改进了筒体结构的动态性能,还节省了材料。实现了轻量化,同时在大大提高了防振性能。

表8 3组优化方案Tab. 8 Three sets of optimization solutions

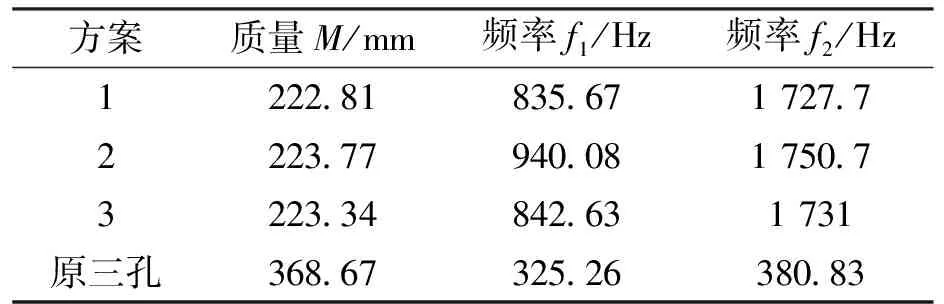
表9 各方案及原设计频率对比Tab. 9 Comparison of each solution to the original design frequency

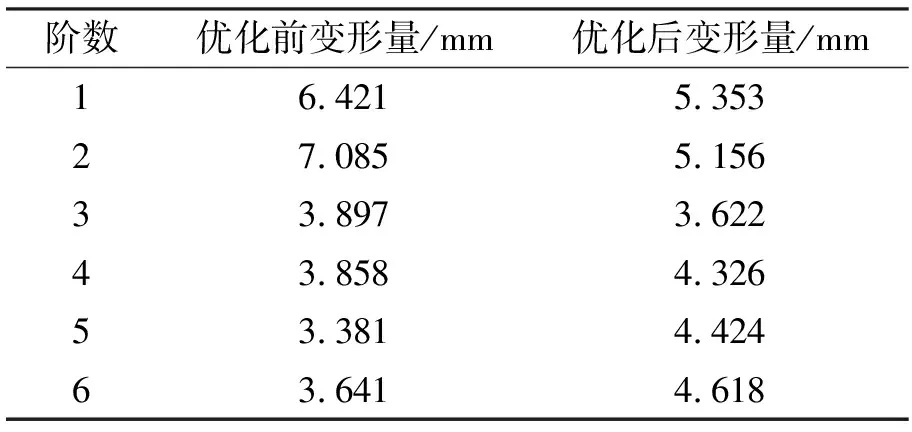
表10 最优方案与原设计振型变形量对比Tab. 10 Comparison between the optimal solution and the original design

4 结论

1) 不同材料属性和结构尺寸对筒体振动性能都有影响,通过考查各个初选变量的灵敏度的方法,以筛选出弹性模量、质量密度以及内径大小、开孔宽度为设计变量,使筒体模态频率和质量优化更有针对性。

2) 运用面心复合设计获取一组样本点,基于构建筒体前两阶固有频率和质量的Kriging响应面模型。此响应面模型拟合度较好,而且显著提高了计算效率,节省了计算时间。

3) 建立多目标优化模型,通过Ansys提供的多目标遗传算法,对筒体模态频率和质量进行了优化,获得最优优化方案,不仅实现了筒体固有频率的大幅度提升,同时大大降低了筒体质量,实现了轻量化。

采用弹性模量为196 GPa,质量密度为7 335 kg/m3,内径为397.85 mm,开孔宽度为307.22 mm的二孔筒体相比于三孔筒体,大幅度提升了管绞车筒体的抗振性能,同时更加轻量化,对整个管绞车设备的抗振性能更是显著性提升,也增加了设备的可靠性。