变换教法策略，培养学生思维

李军

教无定法，贵在得法。实施和利用多种方法教学，需精心设计课堂教学，充分发挥学生的主体作用、教師的主导作用，调动学生学习的主观能动性。

一、重视多种教法引导学生学习

（一）一课多法。即对一课内容可使用多种教法，比如学到三角形的中位线时。

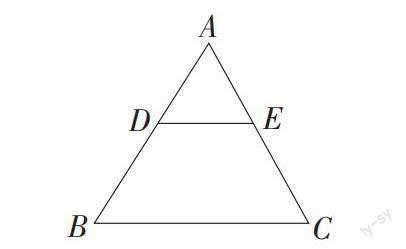
教法一 （发现式）：任意画一个三角形，找出其中两边的中点，并连结中点（如图），用刻度尺量一量DE和BC，看它们的长有何关系？再用量角器量一量∠ADE与∠B，看它们大小有何关系，通过上述操作你得出了什么结论，请与同伴交流，并力争证明你们所得到的结论。

教法二（启发式）：先向学生提出问题串，再让学生通过思考得出结论。1.你是如何理解三角形中位线的？请与同伴交流。2.三角形的中位线有怎样的性质？学生通过带着问题读书，了解三角形中位线这个概念，理解三角形中位线定理，再通过教师示范，掌握定理及其应用。

（二）一知多法。根据学生知识基础和接受能力，对一个知识点的教学采用不同的方法。如教学三角形三内角的和等于180°时，可用以下方法。

教法一（折叠法）：用小刀裁一个三角形，并作一边上的高，标明垂足，把三个角的顶点对着垂足折过去（如下图），学生会惊喜地发现三角形内角和定理。

教法二（测量法）：用量角器测量三内角的度数，再计算三个内角的和。

二、重视一题多证、一题多变，培养学生思维能力

（一）一题多证

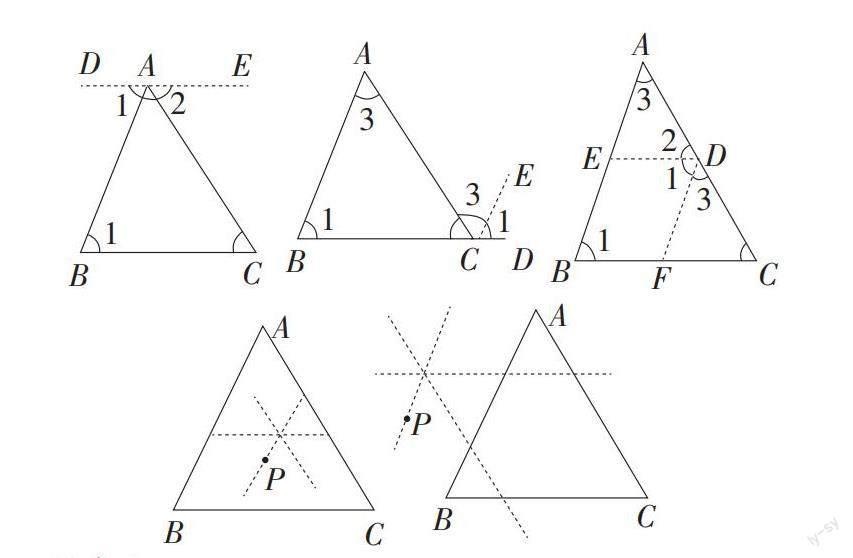
对一个数学命题，从不同角度或用不同方法思考，可得到多种证明方法。如我在八年级上引导学生学习三角形内角和定理的证明时，一共发现了五种证明办法： 1.过A作DE∥BC； 2.过C作DE∥AB；3.过AC上一点D作DE∥BC，DF∥AB；4.在△ABC内过点P作三边的平行线；5.过△ABC外一点P作三边的平行线。

（二）一题多变

在数学教学中，利用变式方法构造变式系列，展示知识的发生发展过程，问题的结构和演变过程，形成数学思维训练的有效模式。

1.[标准题]甲乙两车同时从A、B两地出发，A、B两地相距800km，甲的速度是48km/时，乙的速度是72km/时，问经过几小时两辆车相遇？

2.[条件变式]甲乙两车同时从A地出发，甲的速度是48km/时，乙的速度是72km/时，它们背向而行，几小时相距800km？

三、精心设计分层变式练习题组，改变现有单一题型

习题组设计可包括引进题组、迁移题组、巩固题组、类比题组、特解题组、变式题组、探索题组等等，各种题组的设计一定要注意梯度，控制难度，不同层次的学生都能得到提升。如在讲授平方差公式后，设计如下变式练习题组：

1.[标准题]（2m+3n）（2m-3n）=4m2-9n2

2.[一级变式]（3x+4y）（4y-3x）=16y2-9x2

3.[二级变式]（x+2y）（x2+4y2）（x-2y）=x4- 16y4

四、小组合作策略，旨在帮学

在数学中，有很多规律和定律，如果光靠老师口头传授是起不到作用的。这时候就可以引导学习小组进行合作、开展讨论、共同思考、探索归纳。这样可以培养学生的数学素养，而且还可以培养他们团结合作的能力等。采取小组合作学习法，使得学生共享一个观念，学生们在一起学习。既要为别人的学习负责，又要为自己的学习负责，学生在既有利于自己，又有利于他人的前提下进行学习。

五、积极的评价策略，旨在促学

真诚的激励环境，适时适当的激励，可以起到事半功倍的效果，教学中教师应掌握并运用好这个课堂杠杆，营造一种可以充分发挥学习个性、各抒己见、相互交流的和谐学习氛围。教师一句真诚的表扬、一个赞许的目光……都能使每个学生真切地体验到数学学习的成功与快乐，从而产生强烈的求知欲望。