Wetting-drying-freezing-thawing cycle effect on the hydro-mechanical behaviour of Yanji swelling mudstone

Zhixiong Zeng, Lingwei Kong

a Department of Civil and Environmental Engineering, Hong Kong University of Science and Technology, Hong Kong, China

b State Key Laboratory of Geomechanics and Geotechnical Engineering,Institute of Rock and Soil Mechanics,Chinese Academy of Sciences,Wuhan,430071,China

Keywords:

ABSTRACT Swelling geomaterials in northwestern and northeastern China are exposed to both seasonal wettingdrying (DW) and freezing-thawing (FT) processes.The influence of full-process wetting-dryingfreezing-thawing(WDFT)cycles on their hydro-mechanical behaviour has not been well investigated.In this study, a series of swelling and compression tests was conducted on Yanji weathered mudstone subjected to different WD, FT and WDFT processes and the effects of seasonal processes and cyclic number on the swelling strain, compression index, rebound index and hydraulic conductivity were experimentally determined.With the increasing WD, FT and WDFT cycles, the starting time of primary swelling decreased first due to the increasing water infiltration with the appearance of large pores, and then increased because of the decreasing swelling potential of compact aggregates after two cycles.Moreover,as the cyclic number increased,the final swelling strain declined.Upon loading,the specimens after cyclic processes exhibited a smaller compression index at low stresses due to their smaller interparticle distance after swelling, but a larger one owing to the collapse of large pores and cracks at high vertical stresses.After unloading, the rebound index decreased with the increase of cyclic number due to the irreversible collapse of large pores and cracks.The hydraulic conductivity increased with the increasing cyclic number at low vertical stresses (large void ratios).With the further increase of vertical stress,the increase of hydraulic conductivity induced by cyclic processes became indiscernible.Moreover,a comparison among three processes suggested that the WDFT process exerted a more pronounced influence on the hydro-mechanical behaviour of Yanji mudstone than the separate WD or FT process.

1.Introduction

Swelling rocks and soils are extensively distributed worldwide.They are considered as one of the most problematic geomaterials encountered in construction engineering due to their adverse water sensitivity.Because of containing a great amount of active clay minerals (mainly montmorillonite and illite), these swelling geomaterials can significantly swell and soften upon contact with water,and shrink and crack after desiccation,which are regarded as an important inducement for geotechnical engineering problems(Ajdari et al.,2013;Massat et al.,2016;Zeng et al.,2021).Moreover,the engineering properties of swelling geomaterials can be affected by periodic moisture changes.Over the past decades, numerous studies have been conducted on the swelling and shrinkage properties, hydraulic properties, crack development and strength properties of swelling geomaterials exposed to wetting-drying(WD) cycles (Yazdandoust and Yasrobi, 2010; Tang et al., 2011;Lakshmikantha et al.,2012;Estabragh et al.,2015).It has been well documented that the multiple WD cycles could induce massive irreversible deformation, and create numerous cracks on the surface(Tang et al.,2011).On one hand,such cracks would reduce the shear strength and increased the compressibility, resulting in the uneven settlement of foundations(Saada et al.,1994).On the other hand, they could serve as preferential flow paths for water infiltration and sharply increase the hydraulic conductivity of swelling rocks and soils (Lu et al., 2016), influencing the stability of associated geotechnical infrastructures.

In recent years,many water transfer and transportation projects have been undertaken in northeastern and northwestern China to meet the increasing requirements of economic development, and plenty of geotechnical infrastructures are being constructed in swelling geomaterials areas.In these seasonally frozen regions,the temperature can be below -20°C in winters and over 30°C in summers.Considering the periodic fluctuation of atmospheric temperature as the most destructive action in cold climates, the influence of freezing-thawing(FT)cycles on the hydro-mechanical behaviour of swelling geomaterials has been examined by some investigators(Kong et al.,2018;Zeng et al.,2018;Tang et al.,2018a;Zhu et al., 2022).It was found that the original bonding between particles was greatly altered by newly formed ice lenses during freezing process,and associated large pores and even cracks could develop (Edwin and Anthony, 1979; Lu et al., 2016).These large pores and cracks could facilitate the water flow and lead to a larger hydraulic conductivity after FT cycles(Chamberlain and Gow,1979).Moreover,the presence of large pores and cracks could also weaken the geomaterials in terms of strength and stiffness (Tang et al.,2018b; Lu et al., 2019).Zou et al.(2022) indicated that FT cycles led to less strain-softening behaviour and significant reductions of cohesion and friction angle for Qiqihar expansive soil.Zou et al.(2020) and Zhao et al.(2021) pointed out that the mechanical performance of a Heilongjiang clay decreased significantly,and the water retention capacity and volume change became less sensitive to the water content after FT cycles.Recently, several researchers have noticed that the geomaterials in seasonal frozen regions are exposed to the combined WD and FTcycles rather than the separate WD or FT cycles (Zeng et al., 2018; Zhao et al., 2021).Zeng et al.(2018, 2020) investigated the microstructure features and mechanical behaviour of Yanji weathered mudstone after WD,FT and wetting-drying-freezing-thawing (WDFT) cycles by consolidated drained triaxial compression, scanning electron microscopy (SEM)and mercury intrusion porosimetry(MIP)tests.They found that the microstructure change induced by WD cycles would be amplified by subsequent FT cycles, resulting in a greater reduction of mechanical strength after WDFT cycles.Similar observation was obtained by Zhao et al.(2021) on Qiqihar expansive clay and by Zhu et al.(2022) on Xinjiang expansive clay.However, it should be pointed out that previous studies were limited to the mechanical properties, such as elastic modulus, failure strength, and shear strength.There have been no comprehensive studies to reveal the hydro-mechanical response, in particular the swelling property,compressibility and permeability of swelling geomaterials subjected to WDFT cycles.

This study aims to investigate the influences of WD, FT and WDFT processes on the hydro-mechanical behaviour of Yanji swelling mudstone.The specimens after various WD,FT and WDFT cycles were first hydrated with distilled water, and then subjected to cyclic loading and unloading to clarify the compression and rebound behaviours.The swelling strain, compression index,rebound index and hydraulic conductivity for the specimens after different seasonal processes and cyclic numbers were quantitatively determined,allowing the deterioration mechanism of hydromechanical properties caused by seasonal processes to be thoroughly discussed and analyzed.The outcome from this study helps understand the deterioration mechanism of Yanji mudstone under the climate conditions and provides guidance to minimize the associated landslide risk.

2.Materials and experimental methods

2.1.Materials

In Yanji, China, numerous mudstone cut slopes were formed during the construction of Jilin-Hunchun railway and many of them failed after rainfall events.To uncover the failure mechanism of mudstone slopes, the swelling mudstone was sampled on 12 September 2014 under cool and sunny autumn conditions from a typical landslide at the K275 section.Since extensive excavation and backfilling works were implemented to protect the cut slopes,the mudstone in the site was fully disturbed and crushed.The obtained mudstone has a water content of 20% and a dry density of 1.67 Mg/m3.To represent the site condition,the obtained mudstone was squashed and passed through a 2 mm sieve.The grain size distribution was determined using dry-sieving (for grains larger than 0.075 μm)and hydrometer(for grains smaller than 0.075 μm)methods.As shown in Fig.1,the mean grain diameter and the claysize fraction of tested mudstone are 0.068 mm and 7.4%, respectively.The specific gravity and Atterberg limits of the mudstone were also measured as per ASTM D5550 (2011) and ASTM D4318(2011).The swelling and shrinkage properties of the mudstone were determined by free swelling and linear shrinkage tests.Table 1 lists the basic physical properties of the swelling mudstone.The liquid and plastic limits of the tested mudstone are 41.4% and 15.8%, respectively.From free swelling ratio (54%) and volume shrinkage ratio (14%), the mudstone is characterised by low swell potential.The maximum dry density and optimum water content are 1.72 Mg/m3and 20.6%, respectively.Additionally, randomly selected mudstone (approximately 10 g) was oven-dried for X-ray diffraction (XRD)test.According to the XRD results, the mudstone mainly consists of 23% montmorillonite, 5.2% illite and 23.5%quartz.

2.2.Specimen preparation

During the slope reinforcement in September 2013, the mudstone was crushed and roll-compacted.Since the natural water content was close to the optimum one, no more water was added during the compaction process.In this work, to simulate the field condition,crushed mudstone was humidified by distilled water and the target water content is 20%(corresponding to the natural water content).Then, the mixture was cured for 48 h in waterproof bags to create a homogeneous moisture distribution.Subsequently, the wet mudstone was compacted in oedometer rings to a dry density of 1.67 Mg/m3and the corresponding compaction degree is 97%.The obtained specimens were 79.8 mm in diameter and 20 mm in height.The sample site is characterised by dry cold winters and wet hot summers.The average temperature is -13.2°C in January and 21.7°C in August.More than 80%of annual rainfall occurs in the hot summers.To study the influence of seasonal processes on the hydro-mechanical behaviour of Yanji mudstone, some specimens were exposed to multiple WD, FT and WDFT processes in a temperature and humidity control box (Fig.2a).The temperature and relative humidity were determined based on the weather data of Yanji Basin.For each WD cycle,the specimens were first dehydrated to a water content of 13.9%(corresponding to the shrinkage limit)at a temperature of 25°C and a relative humidity of 75% (Fig.2b).Then,they were wrapped with cling film for 48 h to ensure uniform moisture distribution.Subsequently, the specimens were vacuum saturated and dehydrated to the initial water content (20%).For each FT cycle, the specimens were wrapped with cling film.Then,they were frozen at -15°C for 12 h and thawed at 15°C for 12 h(Fig.2c).For each WDFT cycle, the specimens were subjected to a WD cycles followed by a FT cycle.In this study,the specimens were subjected to 0, 1, 2, 4, 6 and 8 cycles for each kind of seasonal process.A total of 16 specimens were prepared, with 6 specimens for each kind of seasonal process.

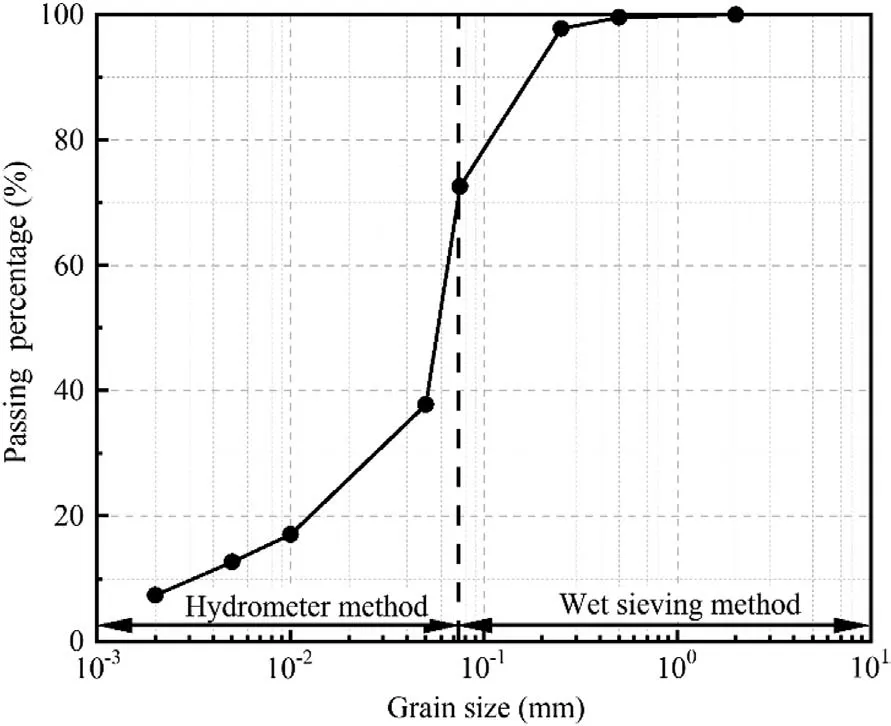
Fig.1.Grain size distribution of the tested mudstone.

Table 1 Geotechnical properties of the Yanji mudstone.

2.3.Experimental methods

With the cyclic processes, specimens might be disconnected from the internal surface of oedometer rings and the lateral surface would be exposed to the cyclic processes.Notably, only the top surface of the mudstone in the field situation was exposed to the seasonal processes.To exclude the influence of lateral cyclic processes, the specimens after prescribed cycles were trimmed carefully by slowly cutting the outer part.The tested specimens were 61.8 mm in diameter and 20 mm in height.Afterwards, the specimens were installed in an oedometer cell (Fig.3).A nominal load was then added on the specimens to ensure full contact.Distilled water was then supplied and the specimens swelled in the axial direction.The swelling was considered to be stable as the vertical deformation rate was smaller than 0.01 mm/2 h.In this study, all the swelling deformation tests ended after 24 h.To investigate the hydro-mechanical behaviour after the stabilisation of swelling deformation, the specimens were subjected to stress-controlled compression.They were loaded to 400 kPa, unloaded to 1 kPa, reloaded to 1600 kPa and re-unloaded to 1 kPa (Fig.4a).At each step, loading level was doubled and unloading level was halved.Each test consisted of 28 steps,and each step lasted 24 h to achieve the stabilisation.

To study the microstructure evolution of the Yanji mudstone under cyclic processes,four compacted specimens with a diameter of 61.8 mm and height of 125 mm were prepared.Three of them were subjected to 8 WD,FT and WDFT cycles in a similar fashion to the specimens for the swelling and compression tests.After that,the microstructures of the specimens before and after cyclic processes were captured using a Quanta 250 scanning electron microscope and an autopore IV 9500 MIP.The specimens were cut into pieces and freeze-dried.For SEM tests, the freeze-dried specimen was peeled for a fresh examination surface, and then the micrographs of swelling mudstone were acquired at a magnification of 2000.For MIP tests,the working pressure rose from 3.6 MPa to 200 MPa and the pores in the range of 350 μm-6 nm were detected.

3.Experimental results

3.1.Swelling strain

The evolutions of swelling strain of the specimens before and after different WD, FT and WDFT cycles are presented in Fig.4b, c and d.Upon hydration, the swelling strain started with a slow increase at the first 1-2 min.Afterwards, the swelling strain increased quickly at an increasing rate(Fig.5).Then,the increasing rate decreased and tended to zero after 61-861 min,with the axial swelling deformation nearly reaching stabilisation.This phenomenon allowed three swelling phases to be defined: initial swelling, primary swelling and secondary swelling (Sridharan and Gurtug, 2004; Ye et al., 2015).As suggested by Zeng and Kong(2019), the swelling strain-log time curves were well fitted by a logistic function:

Fig.2.Wetting-drying (WD), freezing-thawing (FT) and wetting-drying-freezing-thawing (WDFT) processes: (a) Test apparatus, (b) Drying process, and (c) FT process.

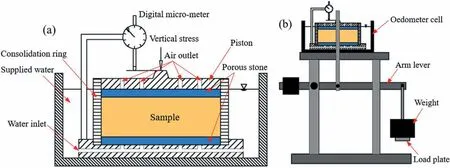
Fig.3.Schematic view of swelling and compression tests: (a) Oedometer cell, and (b) Experimental setup.

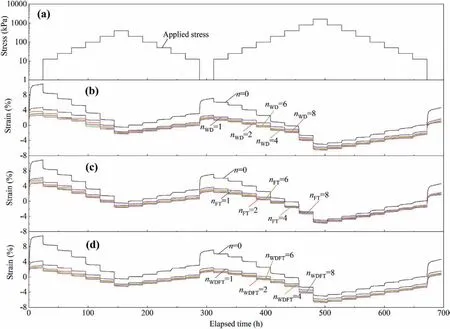
Fig.4.Evolutions of vertical stress and strain with elapsed time for the specimens subjected to various cyclic processes:(a)Vertical stress,(b)After WD cycles,(c)After FT cycles,and (d) After WDFT cycles.Note: nWD, nFT and nWDFT refer to the numbers of WD, FT and WDFT cycles, respectively.

where refers to the swelling strain; t is the elapsed time; and m,ult,0and t1/2are the fitting parameters.Based on two maximum curvature points, three swelling phases were determined.As shown in Fig.5,the arrows indicate the starting and ending times of primary swelling phrase.It appeared that the starting time of primary swelling decreased firstly and then increased with the increasing number of WD, FT and WDFT cycles while the ending time of primary swelling decreased monotonically.The swelling strain-log time curves after a larger number (n) of seasonal processes lied below those after fewer cycles.Additionally,the greater the cyclic number,the smaller the increasing rate of swelling strain.The variation of the final swelling strain with cyclic number is illustrated in Fig.6.For all the seasonal cyclic processes, the final swelling strain declined dramatically at the first four cycles and then became stable.Moreover, a more significant influence on the swelling strain evolution and final swelling strain was observed for the specimens subjected to WDFT cycles compared to those after separate WD cycles and FT cycles.

Fig.5.Evolution of swelling strains with elapsed time for the specimens subjected to cyclic processes: (a) WD cycles, (b) FT cycles, and (c) WDFT cycles.

Fig.6.Relationship between the swelling strains and cyclic number.

3.2.Compression and rebound behaviours

Subsequent to the stabilisation of swelling deformation, cyclic loading and unloading were applied to the specimens.Fig.4b,c and d displays the evolutions of compression strain with elapsed time for the specimens subjected to WD, FT and WDFT cycles.The compression strain-elapsed time curves of the specimens shifted downward after cyclic processes due to their smaller swelling deformation.The WDFTcycles had a more pronounced influence on the compression deformation than either WD or FT cycles did.The void ratio (e)-vertical stress (σv) curves on the loading and unloading paths for the specimens subjected to WD,FT and WDFT processes are presented in Fig.7.All the specimens exhibited convex compression curves with a smaller slope at the beginning of loading and a lager one at high vertical stresses.Upon unloading,evidently linear rebound curves could be observed.

As shown in Fig.7, the yield stress, a threshold stress at which the curvature of the compression curve changed, could be determined.For the specimens subjected to WD,FT and WDFT processes,the yield stress increased with the increasing cyclic process.Moreover, the specimens subjected to WDFT process possessed a larger yield stress due to their less swelling deformation of specimens after hydration compared to those subjected to WD and FT cycles.To further clarify the influences of cyclic processes on the compressibility, the slopes of the linear portion of compression curves, which were termed as compression index (Cc), were determined.Note that the specimens were subjected to two loading and unloading cycles in this study.At the first loading/unloading cycle, the specimens were loaded to 400 kPa, and their void ratios decreased from the maximum value after swelling to those lower than initial one.At the second loading/unloading cycle,they were reloaded to 1600 kPa to identify the influences of cyclic processes.Fig.8 illustrates the variations of the compression index with the cyclic number on two loading paths.At the first loading/unloading cycles (vertical stress smaller than 400 kPa), the compressibility of specimens decreased with the increasing number of cyclic processes due to their lower swelling deformation upon hydration.As regards the second loading/unloading cycle(vertical stress greater than 400 kPa),a slightly larger compression index could be identified,compared to that at the first cycle.For all the cyclic processes,the compression index increased significantly with the cyclic number and reached an almost constant value after four cycles.

The rebound index (Cs), which corresponded to the slopes of rebound curves at vertical stresses larger than 12.5 kPa, was also determined for all the specimens.The variation of rebound index with cyclic number for the specimens subjected to distinct seasonal processes is shown in Fig.9.The rebound index of specimens unloaded at two stress levels of 400 kPa and 1600 kPa increased with the increasing number of cyclic processes.This suggested more irreversible deformation for the specimens after WD, FT and WDFT cycles.For all the specimens, the rebound index corresponding to a vertical stress of 1600 kPa was larger than that corresponding to a low vertical stress of 400 kPa.The void ratio after loading/unloading cycles declined with increasing WD, FT and WDFT cycles.Furthermore, the WDFT cycles exerted a most significant influence on the rebound behaviour,while the effect of the FT cycles was the weakest.

3.3.Hydraulic conductivity

In light of Terzaghi’s one-dimensional consolidation theory,the hydraulic conductivity of specimens during consolidation process can be estimated using the following equation:

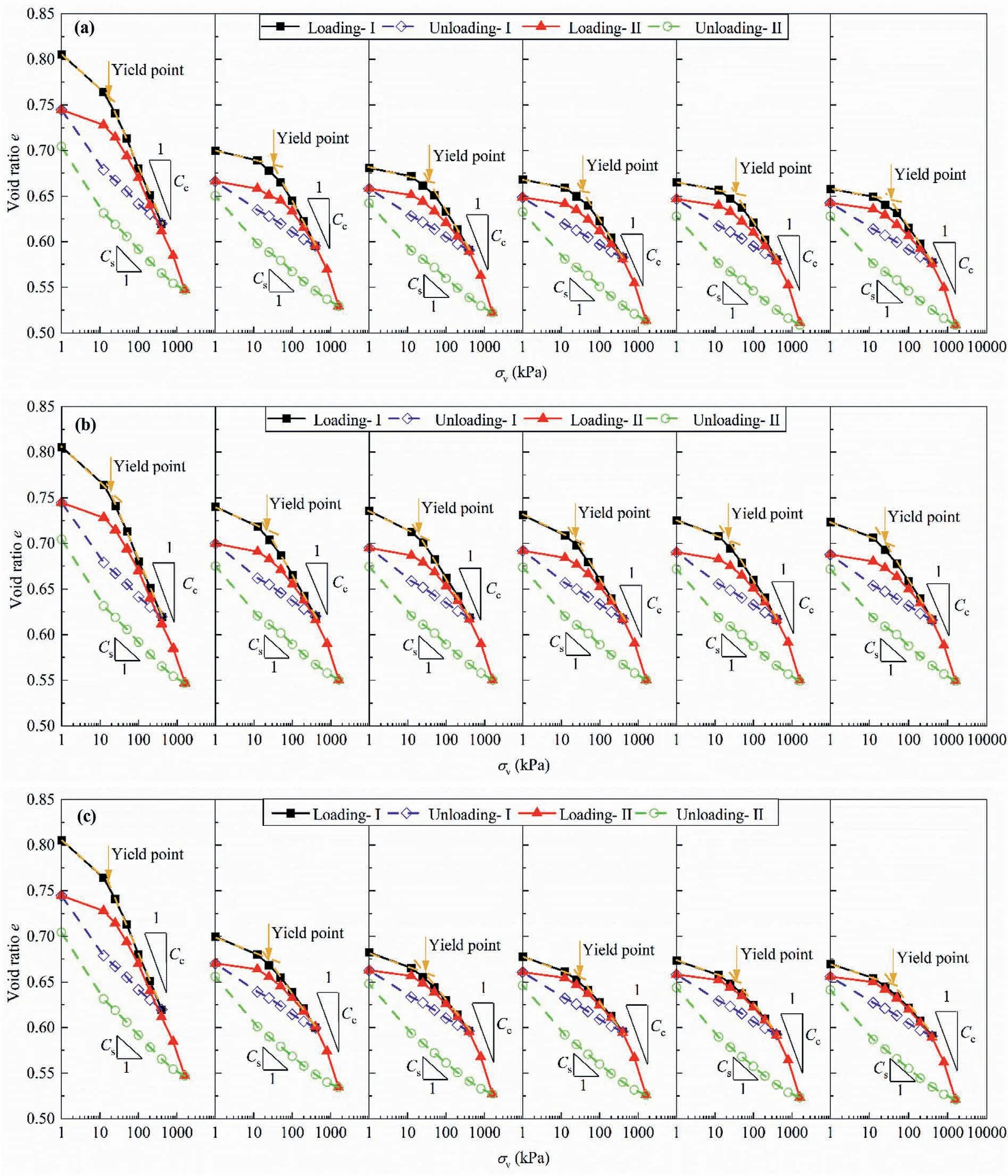
Fig.7.e-log10σv curves for specimens before and after cyclic processes: (a) WD cycles, (b) FT cycles, and (c) WDFT cycles.

where γwis the water density,Eodois the oedometer modulus,and Cvis the consolidation coefficient.The oedometer modulus is defined as follows:

where eirepresents the void ratio of the specimen at the beginning of each loading step,dσ′vcorresponds to an effective vertical stress increment,and de is the void ratio change induced by the effective vertical stress increment.According to the compression curves(Fig.7), the oedometer modulus for the specimens subjected to different WD, FT and WDFT cycles could be determined.The variation of oedometer modulus with vertical stress for the specimens subjected to different WD,FT and WDFT cycles is shown in Fig.10.The oedometer modulus followed an almost linear relationship with the vertical stress.With the increase of cyclic number, the oedometer modulus at low vertical stresses (less than 800 kPa)increased,while it decreased at large vertical stresses(1600 kPa).A comparison among three cyclic processes revealed that the WDFT cycles exerted the most significant influence on the oedometer modulus while the FT cycle did the least.

Fig.8.Variation of compression index Cc with the number of cycles at various stress levels of (a) 0-400 kPa, and (b) 400-1600 kPa.

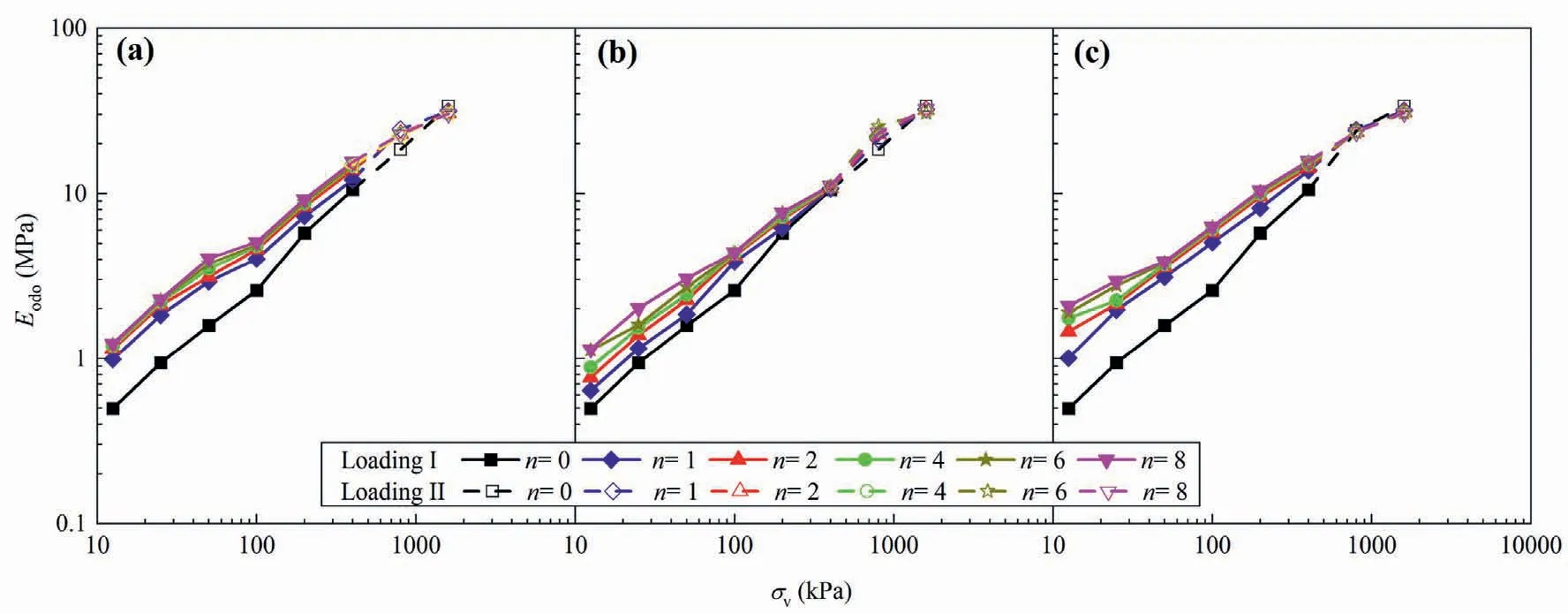
Fig.10.Variation of oedometer modulus with vertical stress on loading paths for the specimens subjected to (a) WD cycles, (b) FT cycles, and (c) WDFT cycles.

The consolidation coefficient was also determined from the compression strain-elapsed time curves(Fig.4b,c and d)following the Casagrande’s log-time method and the calculated results are summarised in Fig.11.The consolidation coefficient decreased with the increasing number of cyclic processes.At the low vertical stresses, the consolidation coefficient of the specimen without cyclic processes was apparently larger than those of the specimens after cyclic processes due to its high porosity after swelling.As the vertical stress increased, the specimens after cyclic processes exhibited a smaller decreasing rate of consolidation coefficient.Consequently, the consolidation coefficient of all the specimens became similar at a large vertical stress of 1600 kPa.

The hydraulic conductivity was then calculated using Eq.(2).The relationships between the hydraulic conductivity and void ratio for the specimens before and after distinct cyclic processes are illustrated in Fig.12.As expected, the calculated hydraulic conductivity increased with increasing void ratio for all the specimens.At large void ratios,the specimens after cyclic processes displayed a larger hydraulic conductivity than those without cyclic processes.With the increasing number of cyclic processes, the hydraulic conductivity increased.Moreover, a more significant increase was observed for the specimens after WDFT cycles.As shown in Fig.12c,the hydraulic conductivity of specimens after eight WDFT cycles was eight times larger than that for the specimens without cyclic processes at the same void ratio of 0.67.However, the increases were found to be indiscernible as the void ratio decreased to 0.59,0.64 and 0.58 in the case of WD,FT and WDFT cycles,respectively.

4.Interpretation and discussion

Basically, the macroscopic hydro-mechanical response of swelling mudstone is highly dependent on its microstructure features.Fig.13 compares the SEM micrographs of the specimens before cyclic process and after eight WD, FT and WDFT cycles.It clearly showed that the specimen without cyclic treatment presented an unordered flocculated structure constituted by the schistose and flat particles.After cyclic WD and FT processes,extensive fissures/cracks and large pores could be identified and aggregates were dispersed by cracks and voids.Moreover, larger numbers of fissures/cracks and voids were generated for the specimens subjected to WDFT cycles compared to those subjected to separate WD or FT cycles.This phenomenon could be confirmed by the MIP results in Fig.14.Based on the studies of Thom et al.(2007), intra-aggregate and inter-aggregate pores could be separated by 2 μm.As shown in Fig.14,the WD,FT and WDFT processes decreased the intra-aggregate volume but increased the interaggregate volume.Moreover, the influence of WDFT cycles on the pore size distribution was more significant than those of WD and FT cycles.This phenomenon was ascribed to the rising suction upon drying and the creation of ice lenses after freezing.Upon drying,soil suction increased, and held the particles together.As a result,fissures/cracks would appear as the increasing tensile stress exceeded the tensile strength (Fig.15b) (Péron et al., 2009; Tang et al., 2011).These fissures/cracks could destroy the bonds between aggregates.During freezing,the pore water in the specimens would be frozen with an increase of volume.The specimen pores would be expanded by the formation of ice lenses and even a number of cracks/fissures could also appear after FT process(Fig.14c) (Lu et al., 2016).For the WDFT process, the pre-existing fissures/cracks after WD cycles would be further enlarged by the FT cycles.Consequently, a larger inter-aggregate volume was identified after WDFTcycles.Furthermore,the rising suction during drying and the expanding stress imposed by the ice lenses during freezing led to the void collapse inside aggregates, and the aggregates tended to be more compact with the reduction of intraaggregate volume after WD, FT and WDFT cycles (Fig.14).

4.1.WDFT cycle effect on the swelling strain

As the specimens subjected to WDFT cycles were hydrated with water, the presence of large voids and fissures/cracks would accelerate water infiltration into the specimens, decreasing the starting time of primary swelling stage.Simultaneously, the clay particles adjacent to fissures/cracks and voids firstly swelled to fill fissures/cracks and voids(Yuen et al.,1998), and then the swelling deformation became measurable,giving rise to the starting time of primary swelling stage.Therefore, the starting time of primary swelling stage decreased firstly and then increased with the increase of cyclic number (Fig.5).Additionally, when water first entered the inter-aggregate pores of specimens and then infiltrated into the intra-aggregate and inter-layer pores (Tang et al., 2011), a smaller aggregate surface area was available for interaction with water for the specimens after cyclic processes due to the increasingly compact aggregates(Al-Homoud et al.,1995;Zeng and Kong,2019).Thus,a shortened time was needed to achieve a nearly stable state after hydration(Fig.5).Moreover,the reduced contact surface area could also reduce the swelling potential and resulted in a reduction of final swelling strain(Fig.6).

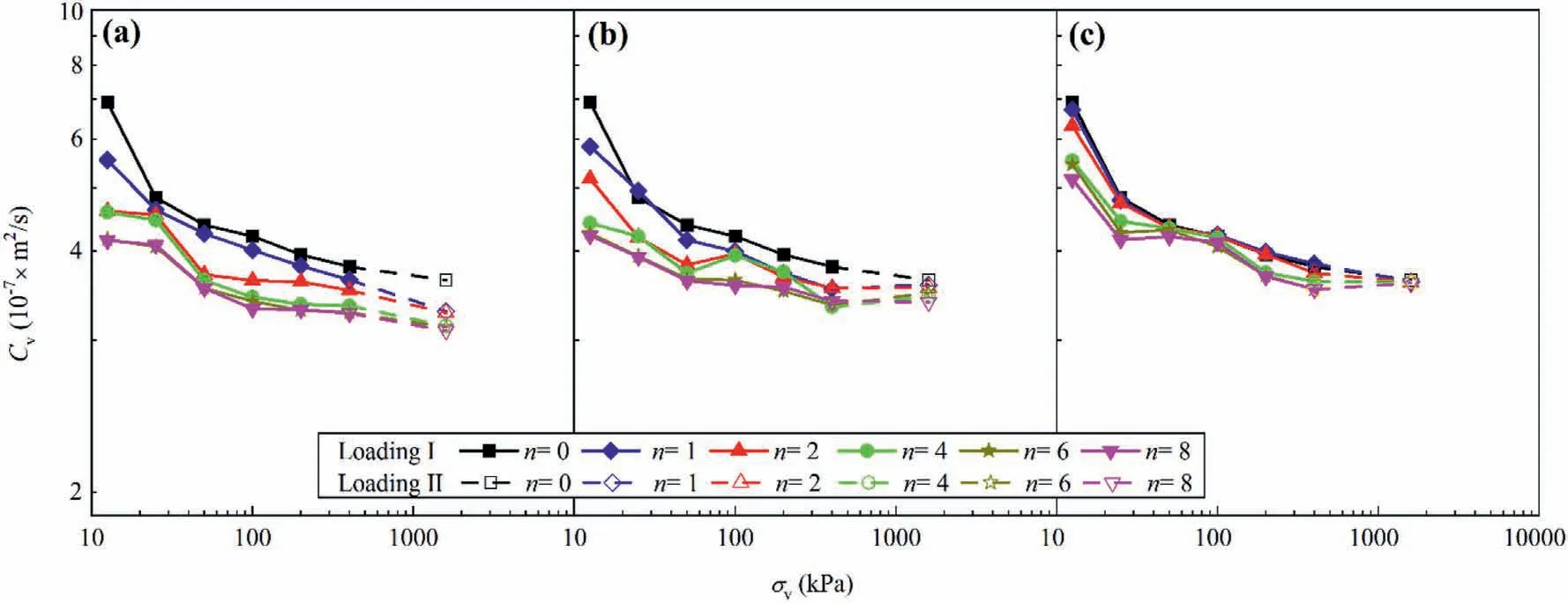
Fig.11.Variation of consolidation coefficient with vertical stress for the specimens subjected to (a) WD cycles, (b) FT cycles, and (c) WDFT cycles.

Fig.12.Relationship between hydraulic conductivity and void ratio for the specimens subjected to (a) WD cycles, (b) FT cycles, and (c) WDFT cycles.

Fig.13.SEM micrographs of the swelling mudstone: (a) Before cyclic processes, (b)After 8 WD cycles, (c) After 8 FT cycles, and (d) After 8 WDFT cycles.

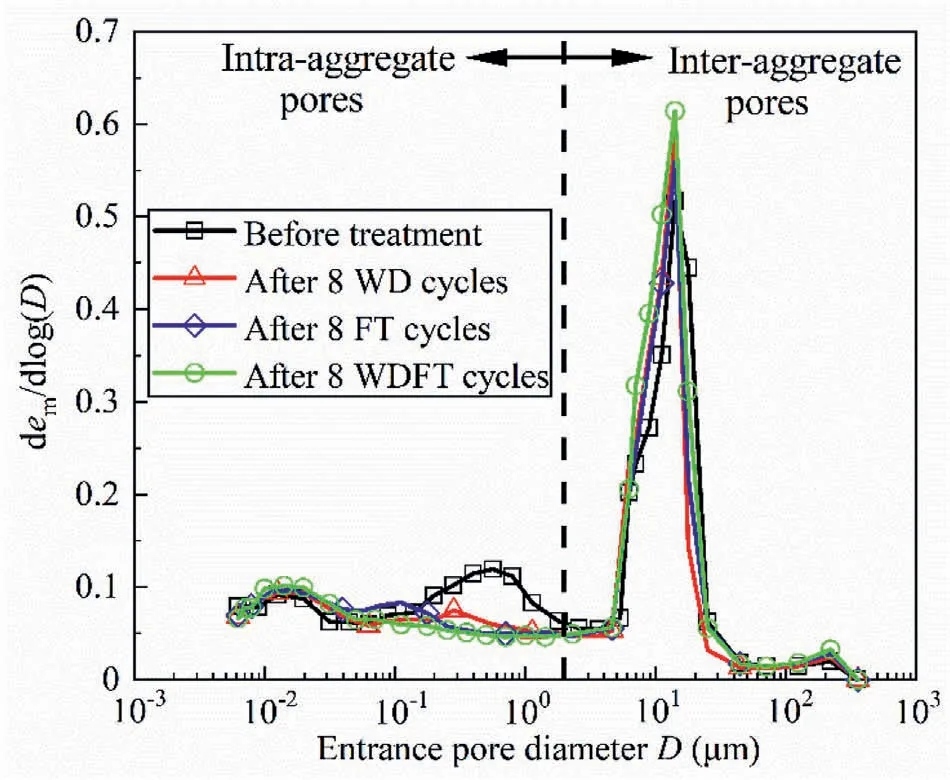
Fig.14.Pore size distribution curves of the specimens before and after 8 WD, FT and WDFT cycles.

4.2.WDFT cycle effect on the compressibility

From Fig.8, there seemed to be a critical vertical stress(400 kPa),suggesting two phases for the compression behaviour of the specimens after cyclic processes.In the case of low stresses(below the critical stress), the compressibility of the specimens after cyclic processes was larger than that of the specimens without cyclic processes;by contrast,in the case of higher stresses(beyond the critical stress), an opposite trend could be identified.This critical stress was close to the swelling pressures, which allowed the specimens to recover to their initial volume.As remarked earlier, the specimens without cyclic processes exhibited a noticeably larger swelling deformation than those after cyclic processes during hydration (Fig.6), and thus a larger spacing between particles and a smaller skeleton structure resistance could be expected for the specimens without cyclic processes (Zeng et al., 2019).When a surcharge vertical stress lower than the critical stress was added,a more significant collapse of the inter-particle spacing and a lower yield stress were expected for the specimens without cyclic processes.Thereafter, the specimens without cyclic processes showed a greater decreasing rate of void ratio and a higher compression index at low stresses (Fig.8a).With the further increase of applied vertical stress(larger than the critical stress),the void ratio of specimens decreased to lower than their initial void ratio and the compressibility became conditioned by the fabric and structure (Baille et al., 2010).For the specimens after WD, FT and WDFT cycles,the large pores and cracks induced weak zones inside the specimens, which were prone to be compressed by the increasing vertical stress (Saada et al.,1994) compared to the homogenous microstructure of the specimens without cyclic processes.As a result,the void ratio of the specimens at a vertical stress of 1600 kPa decreased with increase of WD, FT and WDFT cycles.The specimens after cyclic processes exhibited a larger compression index at high vertical stresses, especially for those subjected to WDFT cycles (Fig.8b).Furthermore, after unloaded to zero, the specimens after cyclic processes displayed lower redound index and final void ratio than those without cyclic processes, even though they had similar void ratios before the oedometer tests.This indicated that most inter-particle relative movement took place during loading owing to the collapse of fissures/cracks and large pores, which was irreversible after unloading.

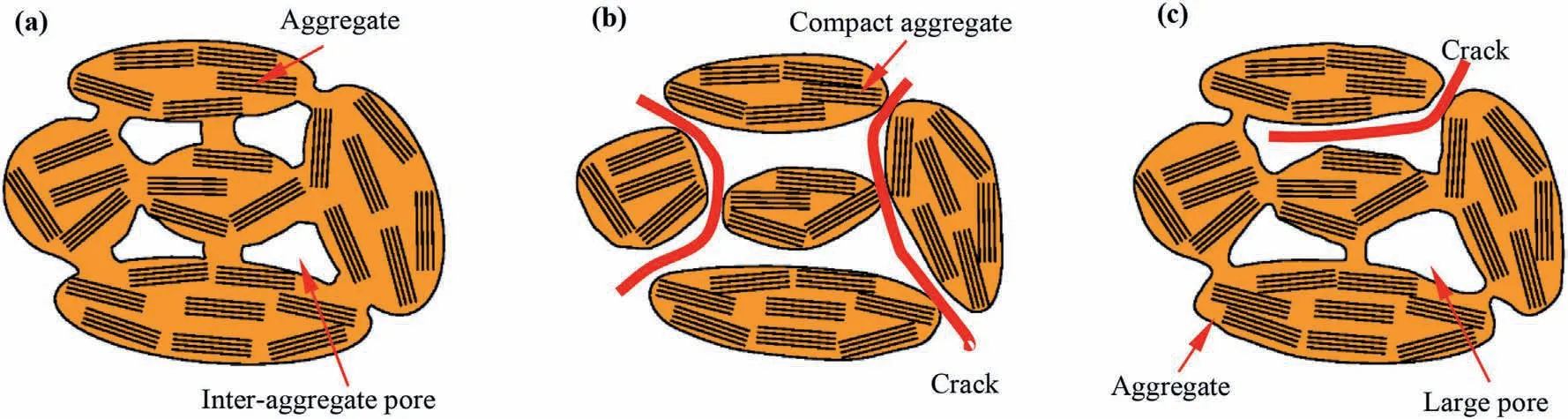
Fig.15.Schematic fabric and pore spaces of representative elementary volume for the swelling mudstones subjected to WD and FT cycles:(a)Initial state,(b)After WD cycles,and(c) After FT cycles.

4.3.WDFT cycle effect on the hydraulic conductivity

Unlike the swelling deformation, the cyclic processes led to an increase of hydraulic conductivity (Fig.12).Cuisinier et al.(2011)found that water flow through compacted soil was preliminarily governed by the inter-aggregate volume when they evaluated the hydraulic conductivity from pore size distribution.Bian et al.(2022)correlated the hydraulic conductivity with the large-pore volume for superabsorbent polymer stabilized soils subjected to WD cycles and indicated that the hydraulic conductivity increased with the amount of cracks induced by WD process.In a similar fashion, the appearance of large pores and cracks induced by FT cycles could significantly increase the hydraulic conductivity by one to two orders of magnitude(Kim and Daniel,1992;Hewitt and Daniel,1997;Rowe et al.,2017;Dalla Santa et al.,2020).For the Yanji weathered mudstone, the WD, FT and WDFT cycles led to a huge number of large pores and cracks and increased the inter-aggregate spacing(Fig.14),which provided preferential flow paths for water transfer and facilitated the water flow through the specimens.Therefore,the larger the number of cyclic processes, the higher the interaggregate volume and the greater the hydraulic conductivity,especially at large void ratios (Fig.12).Additionally, the WDFT cycles had a more significant influence on the hydraulic conductivity because of the more significant variation of inter-aggregate spacing.In the case of low void ratios (large vertical stresses), the influence of cyclic processes on the hydraulic conductivity would be reduced or even eliminated owing to the collapse of fissures/cracks and large pores under surcharge stresses.From a practical point of view, the hydraulic conductivity is another factor to be considered in the stability assessment of mudstone slopes.Due to the appearance of large pores and cracks after cyclic processes,the increase of hydraulic conductivity would accelerate the water infiltration into the mudstone slopes after rainfall and increase the pore-water pressure level, resulting in a decrease of the effective resistance force.Meanwhile, the seepage water flow inside the slopes would increase the sliding force.Both of them reduced the stability of the mudstone slopes (Mukhlisin and Taha, 2010).

5.Conclusions

The effects of multiple WD,FT and WDFT cycles on the swelling strain, compression index, rebound index and hydraulic conductivity of Yanji weathered mudstone were examined by performing swelling and compression tests.The results allow the following conclusions to be drawn:

(1) WD, FT and WDFT cycles could induce larger pores and cracks, and facilitate water infiltration into the specimens,leading to a first reduction of the starting time of primary swelling.With the further increase of WD, FT and WDFT cycles, extensive larger pores and cracks appeared, and a longer time was required to detect the swelling deformation as clay minerals first swelled to fill these larger pores and cracks.Moreover, the swelling potential decreased with the increase of cyclic number owing to the contraction of aggregates and a lower final swelling strain was observed after cyclic processes.

(2) Due to lower swelling deformation, the specimens after cyclic processes displayed a smaller inter-particle distance and a lower compression index at the beginning of loading.As the vertical stress was beyond the specimen swelling pressure, the influence of weak zones induced by large pores and cracks became dominant and a larger compression index was observed for the specimens after cyclic processes.Upon unloading, a lower rebound index and a smaller final void ratio were identified due to the irreversible collapse of large pores and cracks.Additionally, the specimens subjected to WDFT cycles exhibited larger compressibility and irreversible deformation than those after WD or FT cycles.

(3) The large pores and cracks could provide preferential flow paths for water transfer, giving rise to the hydraulic conductivity of specimens.Upon loading, the void ratio decreased and the increase of hydraulic conductivity became indiscernible.A comparison among distinct cyclic processes revealed that the WDFT had the most remarkable influence on the hydraulic conductivity.

(4) According to the test results, the decreasing mechanical behaviour after cyclic processes would reduce the mechanical resistance of the mudstone slopes while the increasing hydraulic conductivity could give rise to the sliding force, both of which impaired the stability of the mudstone slopes.

Notably, the deterioration mechanism of hydro-mechanical behaviour of Yanji mudstone under cyclic processes was experimentally determined in this work.In practice, the influences of cyclic processes can be related to the stress and hydraulic boundary conditions of the mudstone.The hydro-mechanical behaviour of mudstone under various stress and hydraulic conditions subjected to cyclic processes will be accessed in further work.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

The authors wish to acknowledge the financial support of the National Key Research and Development Program of China (Grant No.2019YFC1509901).