城市道路应急车辆借道通行与信号协同优化模型

龙科军，张仲根，刘洋，高志波*

(长沙理工大学，a.智能道路与车路协同湖南省重点实验室；b.交通运输工程学院，长沙 410114)

0 引言

应急车辆在火灾、急救等突发事件救援时，花费时间越短事件严重程度越低[1]。然而，随着汽车保有量的增加，城市拥堵不断加剧，交叉口作为出行瓶颈，拥堵尤其严重[2]，导致应急车辆救援花费时间长。尽管《道路交通安全法》规定应急车辆优先通过交叉口，但应急车辆在交叉口的延误仍十分严重。因此，如何降低应急车辆在交叉口的延误成为亟待解决的难题。

近年来，研究人员对交叉口信号优先控制解决应急车辆延误问题展开了大量的研究，主要运用绿灯早启、延长和插入相位等方法[3]，帮助应急车辆快速通过交叉口。Huang等[4]使用时间Petri网于信号优先控制中，根据路段实时状态，灵活调整信号优先方案。Qin等[5]提出车辆分组策略与信号控制方案协同清空车道，实现应急车辆优先通过交叉口。Su等[6]在分散式强化学习框架下，提出考虑应急车辆路线的绿灯抢占方法，降低出行延误。上述研究在应急车辆优先问题中未考虑社会车辆，但保障交叉口社会车辆通行效率是极具现实意义的。目前，已有少部分学者关注到这个问题，如Min 等[7]通过路径搜索算法不断更新最可靠路线，并采用弹性信号抢占方法减少应急车辆优先造成的负面影响。Cao等[8]提出了一种应急车辆信号优先的信号控制策略，确保应急车辆快速通过交叉口，同时缓解冲突方向堵塞。然而相关研究仍基于固定的信号配时模式，随着交叉口流量的增加，应急和社会车辆的出行效率不断降低，迫切需要扩展新思路。

逆向左转车道可以提高交叉口的通行能力，并已在中国超过80个城市中广泛应用。Wu等[9]建立左转通行能力的估计模型并使用现实数据校正，发现逆向左转车道有效提升左转通行能力。慈玉生等[10]提出基于感应控制的逆向可变车道方案，保证交叉口整体效率的同时提高左转通行效率。逆向左转车道有车辆数量少，独立性强，便于预信号控制等特点[11]，可以实时调整车道开启、关闭时间，动态分配车道资源，满足不同交通需求。

综上，当交叉口流量过大时，现有研究对应急车辆被前方社会车辆阻挡造成的延误问题，尚未得到很好解决。同时现有模型对社会车辆干扰明显，导致整体效益受损。基于此，本文提出应急车辆借道通行与信号协同优化模型。在保障应急车辆优先的基础上，以社会车辆出行总时间最小为目标，将应急车辆速度、预信号与交叉口信号配时方案协同优化，提高交叉口整体效益。

1 问题描述与假设

1.1 问题描述

如图1所示，在交叉口路段上设置预信号控制逆向左转车道。本文研究问题归纳为：在路段上，如何优化应急车辆的速度引导策略和预信号控制方案，以实现应急车辆通过路段时间最少；在交叉口插入应急相位后，如何优化交叉口信号配时方案，在保证应急车辆优先的基础上，最大化社会车辆效益。

图1 交叉口场景Fig.1 Intersection scene

1.2 模型假设

参照相关文献[12]，做出以下假设：

(1)应急车辆具有网联功能，可实时接收控制指令并完成速度引导。

(2)在交叉口区域，可以通过智能路侧设备实时检测社会车辆速度与位置。

2 应急车辆借道通行与信号协同优化模型

2.1 应急车辆借道通行模型

(1)逆向左转车道

d为交叉口4 个方向的进口道，d∈{E,W,S,N}。进口道可设置逆向左转车道且允许应急车辆借用通过，车道有直行、左转、逆向左转和应急功能，符号设置为Ω∈{1,2,3,4} 。

当应急车辆进入速度引导区域时，车道功能由逆向左转变为应急，满足约束为

逆向左转车道长度设置影响交叉口时空资源的合理分配。依据冲击波理论[13]，以车流为饱和流率通过交叉口为目标，设计逆向左转车道长度LR为

式中：LR为逆向左转车道长度；Ql为一个周期的左转交通量(pcu·h-1)；h0为车头时距；n1、n2为左转、逆向左转车道车辆数；k1、k2、k3和q1、q2、q3分别为停车、半饱和流、饱和流状态下的交通流密度和流率。

(2)应急车辆车速引导

如图2所示，应急车辆受前方车辆阻挡和应急车道开启位置的制约，在速度引导区域的最小出行时间固定。同时，预信号控制清空应急车道，应急车辆车速越高在应急车道花费时间越少。因此，将车速引导为最高车速进入应急车道并保持为最优策略。但应急车辆左转时，保持最高车速导致转弯速度过大，容易发生侧翻等事故[14]，故应急车辆需通过速度引导至最大安全车速。综上所述，应急车辆路段速度引导策略划分为图3中4种情况。

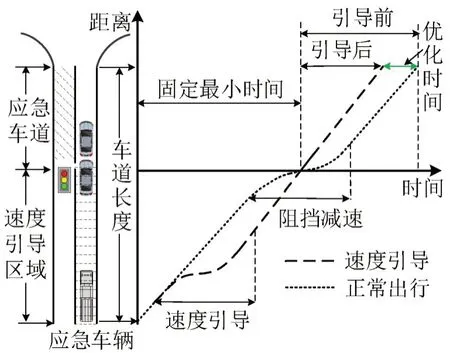
图2 车速引导对比Fig.2 Speed guide comparison

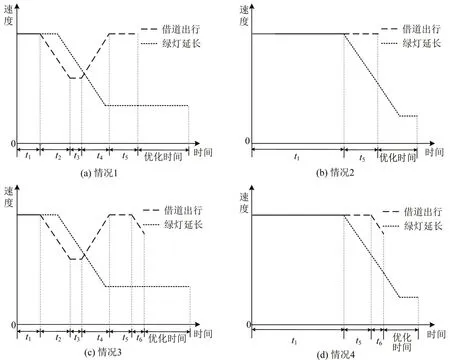
图3 应急车辆车速引导过程Fig.3 Process of emergency vehicle speed guidance

参照Yu 等[15]研究，应急车辆在路段区域的时间和距离公式为

加速度和速度约束为

式中：Le、Lr分别为交叉口车道、速度引导区域长度；te、tr、td分别为应急车辆在交叉口区域、速度引导区域、应急车道的行驶时间；li、ti为i阶段的路程和时间；m为速度引导阶段的集合；分为应急车辆最大加、减速度；、ve(t)、ue(t)分别为应急车辆最大车速，在t时速度和加速度。

情况1 应急车辆通过速度引导区域时，为避免发生碰撞，应满足约束为

应急车辆保持最大车速通过应急车道和交叉口内部区域，满足约束为

情况3 应急车辆通过速度引导区域时，避免发生碰撞，相关约束如式(5)所示。应急车辆左转时，需要通过速度引导将车速降至最大安全速度，相关约束为

式中：vsafe为交叉口内部区域的左转最大安全车速。

情况4 应急车辆到达交叉口区域后，保持车速完成借道通行，约束如式(7)所示。但需要将速度引导至最大安全速度通过交叉口，相关约束如式(8)所示。

(3)应急车道预信号控制

当应急车道到达交叉口区域时，逆向左转车道的车道功能变为应急车道，预信号的控制规则为保障应急车辆优先通行，预信号的绿灯开启、持续时间由应急车辆决定。

绿灯开启时间为当应急车辆到达应急车道起始位置时，预信号绿灯开启。故预信号绿灯开启时间等于应急车辆到达应急车道时间，即

绿灯持续时间为应急车辆在应急车道的行驶时间，故预信号的绿灯持续时间为

过去几十年，贵州一直是国内、外观赏石收藏家和石商重要的资源供应产地，贵州观赏石质优价廉，是观赏石市场的抢手货。贵州观赏石一旦走出贵州，其市场价格便水涨船高，常有天价爆出。因此，优质观赏石资源外流十分严重。

2.2 应急信号配时优化模型

(1)信号交叉口相位设置

交叉口信号控制方式以感应式为基础，为满足应急车辆和社会车辆的出行需求，将相位划分为应急相位和普通相位。普通相位的西方向进口道左转相位和直行相位定义为ph1,ph2，按逆时针方向依次定义为j∈{p h1,ph2,…,ph8} 。应急相位符号定义为k∈{e v1,ev2,…,ev8} 。

(2)应急相位绿灯开启和持续时间

(3)普通相位绿灯最早开启时间和最小持续时间

式中：nj为相位j的车辆数量。

(4)相位间冲突关系

为防止车辆在交叉口内部区域发生冲突，分析相位在交叉口的冲突关系，并对存在冲突的信号相位的绿灯时间进行约束，相位间的冲突关系如表1和图4所示。

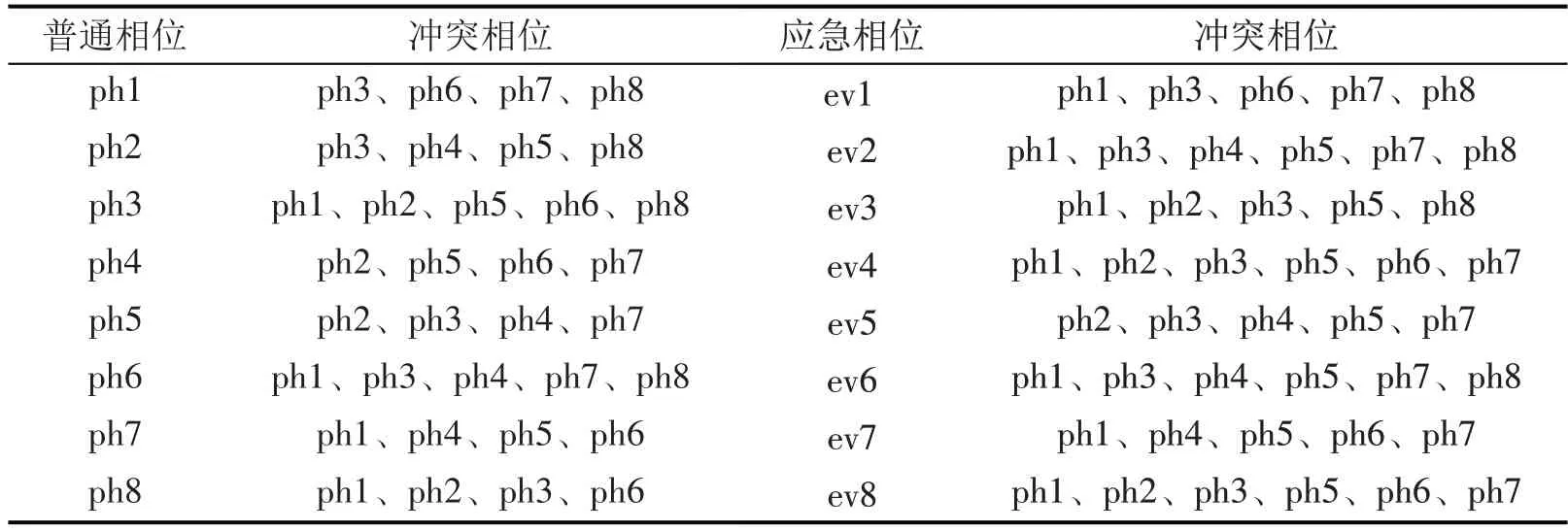
表1 交叉口内部相位冲突Table 1 Intersection internal phase conflict

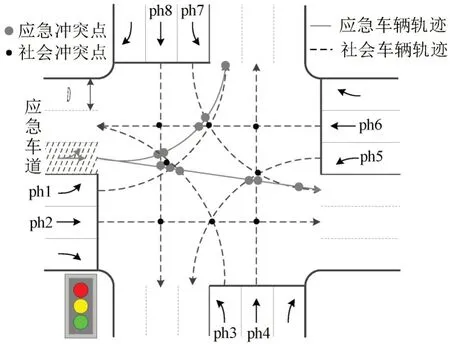
图4 交叉口内部冲突关系(以西方向有逆向车道为例)Fig.4 Intersection conflict relationship(reverse lane in west as an example)

存在冲突的普通相位和应急相位的先后顺序由0-1 变量φ来表示；φ(ev1,ph2)=1 表示应急相位1在普通相位2前开启，否则φ(ev1,ph2)=0 。为了防止冲突相位存在重叠现象，对存在冲突的相位开启时间和持续时间的关系约束为

式中：M为大的正数，本文取9999。

普通相位间的先后顺序由0-1 变量μ表示；μ(ph2,ph3)=0 表示普通相位2 在普通相位3 结束后开启，否则μ(ph2,ph3)=1。存在冲突的相位开启时间和持续时间的关系约束为

式中：j1,j2 分别为存在冲突的先、后相位。

(5)目标函数

模型以最小化社会车辆总出行时间为目标函数，即

3 案例分析

3.1 实验设置与求解

(1)实验设置

如图5所示，实际中逆向左转车道多设置于主干道和次干道相交的交叉口，以此为案例进行分析，参数取值如表2所示。将应急车辆通过交叉口的全过程设为1 组实验。本文随机生成1200 组实验数据，均由一次独立随机抽样生成，主干道和次干道的车道流量抽样范围分别为300～700 veh·h-1和200～400 veh·h-1。社会车辆速度区间为6～10 m·s-1，位置区间为0～200 m。

表2 参数取值Table 2 Parameters used in case study

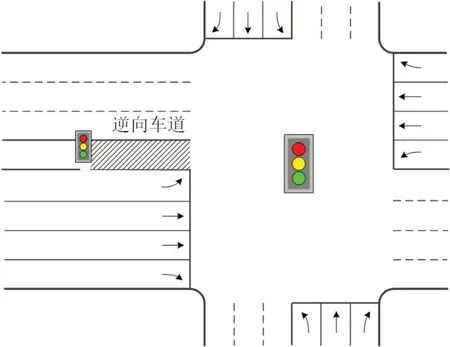
图5 交叉口平面示意图Fig.5 Intersection conflict relationship

(2)模型求解

约束条件：式(1)，式(2)，式(5)～式(20)。

本文通过Python 和AMPL 语言编写应急车辆借道通行与信号协同优化模型，调用CPLEX 求解器快速求解。处理器为11th Gen Intel(R) i5-1135G7，2.40 GHz，16.0 GB内存。求解平均时长小于30 ms，满足实时性需求。

模型求解得到逆向左转车道最优长度为60 m，其余结果在3.2节详述。

3.2 结果分析

为验证模型优化效果，将所提模型与绿灯延长模型对比。绿灯延长模型是通过延长应急车辆所在相位的绿灯时间，保证应急车辆优先通过交叉口，其余相位以社会车辆出行总时间最小为目标，优化绿灯开启、持续时间。

(1)应急车辆出行时间

如图6 和图7 所示，本文模型的应急车辆出行时间全部低于或等于对比模型。应急车辆直行出行时间下降了31.84%、应急车辆左转出行时间下降了29.86%。模型通过车速引导、预信号控制和交叉口相位的协同优化，降低了应急车辆通过交叉口的延误。

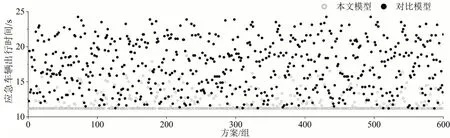
图6 直行应急车辆出行时间对比Fig.6 Comparison of straight emergency vehicles travel time

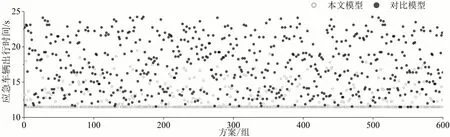
图7 左转应急车辆出行时间对比Fig.7 Comparison of turn left emergency vehicles travel time

(2)社会车辆总出行时间

由图8可知，本文模型与对比模型相比社会车辆总出行时间下降5.73%，应急车辆直行和左转时分别下降10.71%和0.57%。由于应急车辆左转时，占用交叉口时空资源更多，社会车辆收益下降。综上所述，本文模型不仅降低了应急车辆的出行时间，还能实现社会车辆总出行时间的下降。

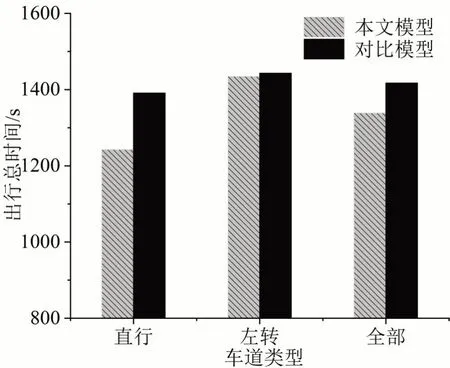
图8 社会车辆总出行时间对比Fig.8 Comparison of social vehicle travel times

3.3 敏感性分析

为进一步分析不同流量和车道长度下的模型效果，绘制图9～图12。由图9可知，随着流量增加，本文模型应急车辆出行时间优化效果更明显。由图10可知，社会车辆总出行时间随着流量增加，本文模型仍优于对比模型。综上，本文模型在不同流量下的优化效果均优于对比模型。

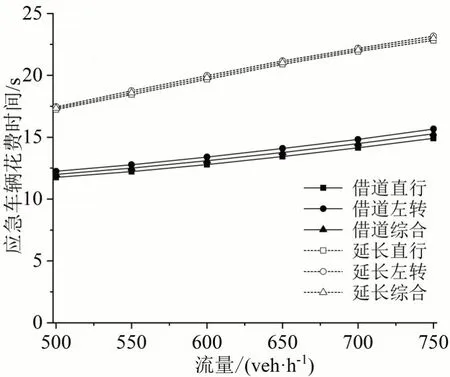
图9 不同流量下应急车辆花费时间Fig.9 Emergency vehicle travel time at varying flow

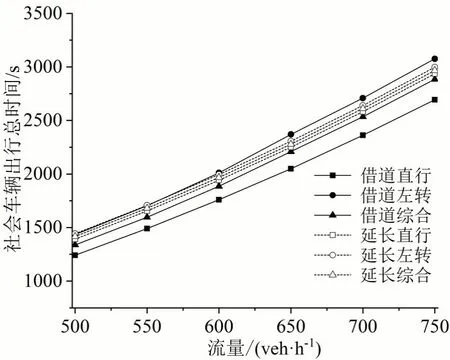
图10 不同流量下社会车辆出行时间Fig.10 Vehicles travel time at varying flow

由图11可知，随着车道长度的增加，本文模型优化效果仍然良好。由图12 可知，社会车辆总出行时间随着车道长度增加后，本文模型相比于对比模型的优化效果明显提升。本文模型在不同车道长度下的优化效果均优于对比模型。

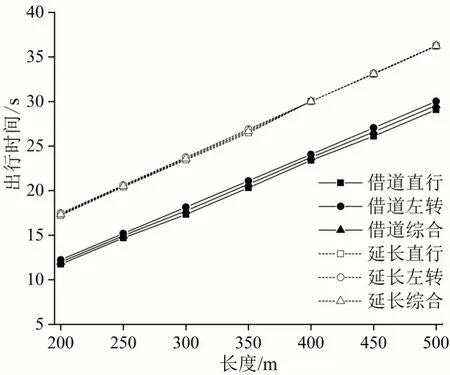
图11 不同车道长度下应急车辆花费时间Fig.11 Emergency vehicle travel time at varying length

图12 不同车道长度下社会车辆出行时间Fig.12 Vehicles travel time at varying length

4 结论

基于应急车辆通过交叉口区域延误过长的问题，本文建立了应急车辆借用逆向左转车道通过交叉口的应急车辆速度、预信号和交叉口信号协同优化模型。

(1)在主、次干道相交的场景下，与绿灯延长模型相比，本文模型降低应急车辆在交叉口30.85%的出行时间，并减少了社会车辆5.73%的出行总时间，表明本文模型不仅可以减少应急车辆的出行时间，还可以改善社会车辆整体效益。

(2) 应急车辆出行时间和社会车辆出行总时间，在不同流量和车道长度的条件下均小于对比模型，表明本文模型在交通拥堵下效果更佳，并在不同交叉口具有普适性。

未来将基于本文研究进一步探索应急车辆在多个交叉口组成的干线或网络的借道优先通行策略。