卫星变轨问题中的4种常见疑难杂症

董廷灿 孙守闯

(1.安徽省明光中学 2.内蒙古扎鲁特旗职业教育中心)

本文通过一道典型例题,结合机械能守恒定律、开普勒行星运动定律和椭圆轨道方程,对症下药,化解有关卫星在以地心为焦点或圆心的若干轨道上变轨过程中遇到的4种疑难杂症.

1 原题呈现

例作为一种新型的多功能航天飞行器,航天飞机集火箭、卫星和飞机的技术特点于一身.假设一航天飞机在完成某次维修任务后,在P点从圆形轨道2进入椭圆轨道1,如图1所示,已知P点距地面的高度为2R(R为地球半径),Q点为轨道1上的近地点,地球表面重力加速度为g,地球质量为M,又知若物体在离星球无穷远处时其引力势能为零,则当物体与星球球心距离为r时,其引力势能Ep＝(式中m为物体的质量,M为星球质量,G为引力常量),不计空气阻力.则下列说法中正确的是( ).

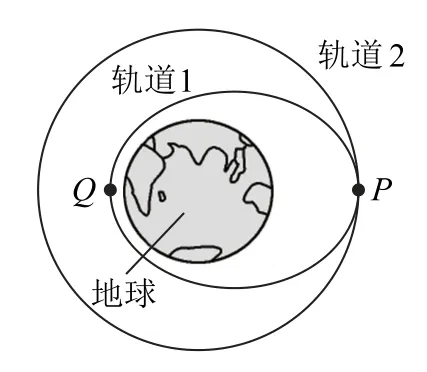
图1

A.航天飞机在轨道1和轨道2上运动时的机械能相等

B.航天飞机运行至Q点的速度小于在轨道2上运行至P点的速度

C.航天飞机运行至Q点的速度不会超过第一宇宙速度

D.航天飞机在轨道1上运行经过P点的加速度等于在轨道2上运行经过P点的加速度

2 问题解析

航天器从轨道2变轨到轨道1时必须在P点点火减速,航天器需要克服反冲力做功,故航天器在轨道1运行时的机械能小于在轨道2上运行时的机械能,选项A 错误;要比较Q点的速度与圆轨道2上P点速度的大小关系,需要作出与Q点相切的近地轨道如图2中虚线所示.

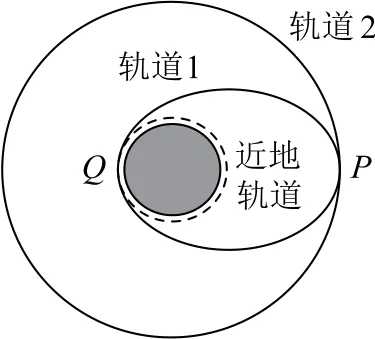
图2

3 疑难杂症

3.1 对症下药,化解对第一宇宙速度是航天器最大运行速度的理解误区

“环绕”释义:沿由路程、行进和旅行所形成的圆圈运动.由此得出环绕速度即卫星围绕地球做匀速圆周运动的速度;物理学家也用环绕速度特指第一宇宙速度,其值为v1＝7.9km·s—1.而运行速度是指卫星绕地球运动的速度,轨道半径不同速度就不同,它可以是一组速度值,环绕速度隶属于运行速度.运行速度一般小于等于最大环绕速度,当卫星沿着椭圆轨道运行时,运行速度可以超过第一宇宙速度,笔者将在3.2中作进一步的定量分析.

3.2 对症下药,化解对切点处加速度的理解误区

由解析可知:卫星在圆轨道和椭圆轨道切点处运行时的引力加速度相等.既然卫星在P点所受万有引力相等,那为什么卫星在轨道2上做匀速圆周运动,在轨道1上却做近心运动? 是不是卫星经过两个不同的轨道到达P点的向心加速度不同呢?

上面的问题涉及卫星的轨道半径和曲率半径的关系.对于轨道2(圆轨道),曲率半径就是圆的半径;设卫星经过P点时的向心加速度为a2n,由,得

对于一般曲线,在不同点的曲率半径一般是不相同的,它表示曲线在该点的弯曲程度.对于椭圆轨道来说,设椭圆的半长轴为a,半短轴为b,椭圆的两焦点F1、F2之间的距离为2c(a＞c),地球位于焦点F1处,如图3所示.

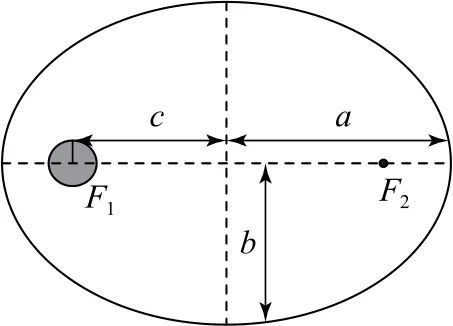
图3

综上可知,椭圆轨道和圆轨道在切点P处的向心加速度也相等,并且等于卫星在该点的引力加速度,即a1＝a2＝a1n＝a2n.

圆轨道中引力加速度等于向心加速度不难理解,椭圆轨道在P点的引力加速度也等于向心加速度难道是数据的巧合吗? 对此,笔者作进一步证明.

设在椭圆运动中,卫星在Q点(近地点)的轨道半径为rQ、运行速度为vQ1;在P点(远地点)的轨道半径为rP、运行速度为vP1.由图3 结合椭圆知识可得rP＝a＋c,rQ＝a—c;同理从P点到Q点,对卫星由机械能守恒定律和角动量守恒定律得

所以卫星在轨道1上P点处的向心加速度为

同时,卫星在轨道2上做匀速圆周运动时,在P点根据万有引力定律提供向心力可得

由式⑥和式⑦可得:在切点P处卫星减速之前的向心加速度a2n和减速之后的向心加速度a1n是相等的,且都等于卫星在P点高度处的引力加速度(在Q点亦如此).

3.3 对症下药,化解对卫星做匀速圆周运动条件的理解误区

椭圆轨道上的近(远)地点的向心加速度与引力加速度相等,为什么卫星会做离心运动或近心运动呢? 如何理解卫星做匀速圆周运动的条件是万有引力等于向心力呢?

关于卫星在椭圆轨道的近地点其万有引力等于向心力,此后为什么会做离心运动,其他文献已做详细介绍,这里不再重复;下面仅就卫星在椭圆轨道的远地点为什么会做近心运动来加以探究.

卫星在P点减速前后,圆周运动中心发生了变化;减速之后,根据式⑥可以发现轨道半径由rP变为ρ.由于rP＞rQ,可得,即卫星在轨道2上的P点减速后,其旋转中心由地球球心变为半径更小的椭圆轨道在P点的曲率圆的圆心,如图4中虚线所示.

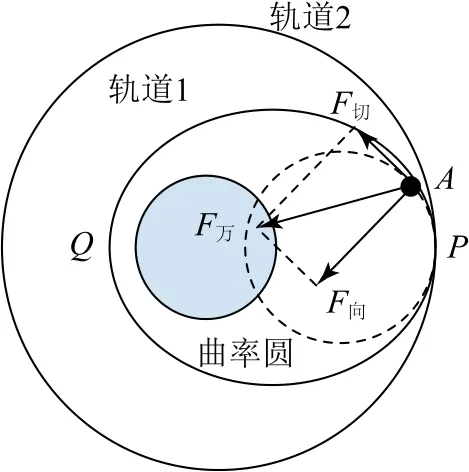
图4

我们可以设想卫星由P点沿曲率圆运动一小段圆弧到达A点,由于卫星所受的万有引力仍指向地心,而地心和曲率圆圆心并不重合,万有引力不再完全充当向心力,另一切向分力将使卫星加速,从而使其做近心运动,即椭圆运动.

综上所述,卫星在椭圆轨道运行时,在近(远)地点处万有引力等于向心力、引力加速度等于向心加速度,离开近(远)地点后,万有引力便不再等于向心力,卫星将做离(近)心运动.这是因为质点做匀速圆周运动的条件是十分苛刻的:质点所受合力方向指向圆心,大小等于质点做圆周运动所需的向心力,并且这个供需关系要始终维持.反之,这种供需平衡一旦被打破,质点将做离(近)心运动.

3.4 对症下药,化解对卫星变轨到达预定点条件的理解误区

欲使卫星从轨道2变轨后能够运行到Q点,难道只能在P点启动发动机提供阻力突然减速,保持速度方向不变使航天器沿着椭圆轨道1运行到Q点? 当然不是.除此之外,还可以通过保持速率不变改变速度方向,或者速度大小方向均改变的方式,笔者将作进一步讨论.

卫星在椭圆轨道运行至短轴端点时,若保持速率不变而改变运行方向,可以使卫星变轨后做匀速圆周运动,且圆周半径恰好等于椭圆的半长轴.由此,我们可以进一步得出若保持速率不变,卫星变轨后能够运行到Q点,必须在轨道2上运行至与椭圆轨道3(椭圆轨道3的半长轴恰好等于圆轨道2的半径)的交点A(B)时改变方向(如图5),且该点为椭圆轨道3的短轴端点.假设卫星在轨道2上逆时针运行,设在B(A)点的速度方向逆时针转过θ,仍以原题为例则a′＝BF1＝3R,c′＝OF1＝2R,由几何关系可知sinθ＝.运行至Q点时的速度大小

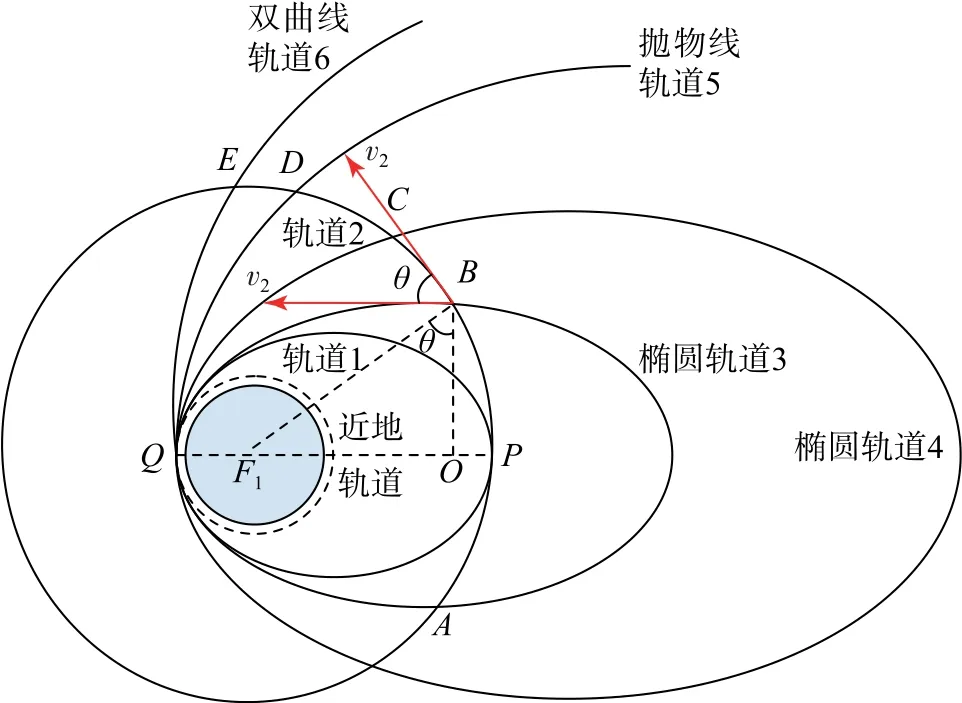
图5

与沿椭圆轨道1运行至Q点时的速度

相比变大了.假如错过了A(B)点,卫星仍可以在任意点C(D或E)点通过同时改变速度大小和方向的方式进行变轨,然后沿椭圆轨道4(抛物线轨道5或双曲线轨道6)运行至Q点;运行至Q点时的速度大小满足

(完)