斜面上平抛运动分类及解题策略
张永强
(山东省荣成市第二中学)
斜面上的平抛运动是各类考试中的常见题型,根据起点、落点的位置,可将其细分为起点在斜面外、落点在斜面上,起落点均在斜面上及仅起点在斜面上三种类型.针对不同题型,解题方法也不相同.本文将系统总结斜面上平抛运动常见题型,并进行分析.
1 起点在斜面外、落点在斜面上
如图1所示是常见的平抛模型,题目中一般会给出落点位置或落点速度等相关信息,解题需要进一步挖掘落点速度方向及水平、竖直位移间的关系.通过矢量三角形,找到斜面与倾角θ之间的关系,此时水平方向有vx=v0,竖直方向有vy=gt,.
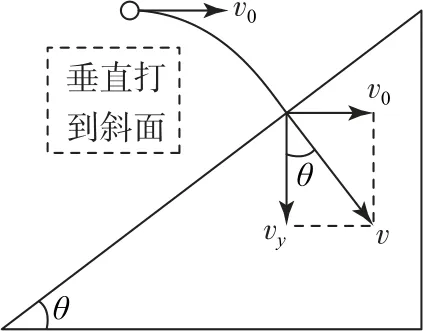
图1
例1如图2 所示,斜面倾角为θ,A上方与斜面等高处的小球以初速度v0向B端抛出,经过t时间后,到达斜面,重力加速度为g,则( ).

图2
2 起、落点均在斜面上
如图3所示,斜面倾角为θ,小球以初速度v0水平抛出,t时刻后落在斜面上另一点,速度为v,与水平夹角为α.根据平抛规律及几何知识可得
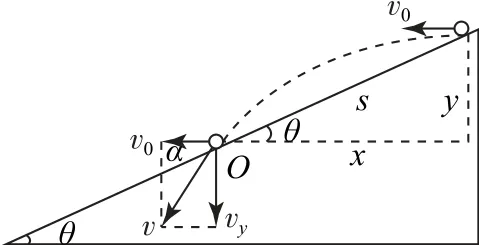
图3
根据上述公式,可以推得二级结论
例2如图4 所示,从倾角为θ的斜面A点两次水平抛出小球,速度分别为v1、v2,落点速度方向与斜面夹角分别 为α1、α2,若v1>v2,则( ).

图4
A.α1>α2B.α1=α2
C.α1<α2D.无法确定
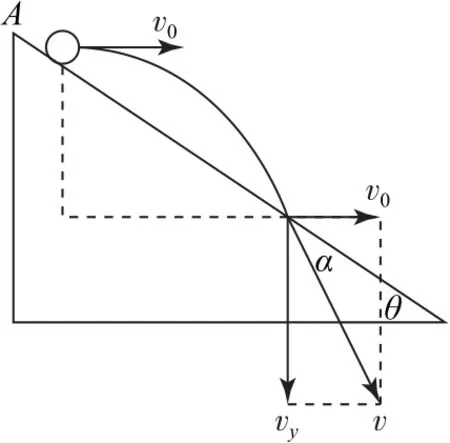
图5
例3如图6所示,斜面上有A、B、C三点,从A、B、C以不同速度水平抛出小球a、b、c,均落到D点,其中AB∶BC∶CD=5∶3∶1,则可得( ).
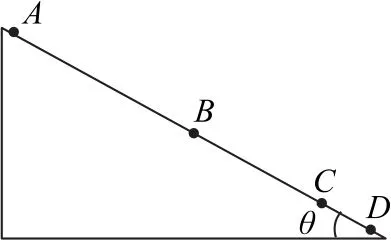
图6
A.a、b、c运动时间比为1∶2∶3
B.a、b、c到达D点时,速度与初速度夹角之比为1∶1∶1
C.a、b、c初速度比为3∶2∶1
D.a、b、c轨迹可能在空中相交
3 起点在斜面上、落点在水平面上
这类题型中,值得注意的是需要充分借助图像知识,挖掘题目中隐含信息.同时,在解答这类问题时,也可以通过辅助线的方法,将其转化为上述两种情况,根据其相关解题策略进行解答.
例4如图7 所示,AB为斜面,BC为水平面,从A点水平抛出两小球,速度分别为v0、2v0,落点与A水平距离分别为x1、x2,则可能为( ).
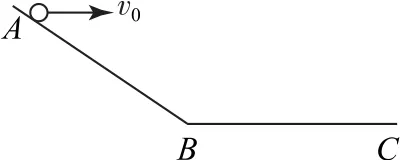
图7
(1)速度为v0、2v0时,落点均在BC上,此时,因为高度相同,所以,两次平抛运动时间相同,水平位移x=v0t,因为小球初始速度为v0、2v0,所以x2=2x1,
(2)速度为v0、2v0时,落点均在AB上,由上述结论可得,小球起点、落点距离
设AB倾角为θ,则起点、落点间水平距离
故
(3)速度为v0时,落点在AB上,速度为2v0时,落点在BC上时,如图8所示,将第一次平抛轨迹延长与BC延长线相交,第二次平抛轨迹延长与AB延长线相交,由(1)可知

图8
由(2)可知
故正确答案为A、B、C.
综上所述,不同类型的斜面平抛运动模型有着不同的解题思路与策略,若学生能够熟练掌握不同题型的解题方法,再面对相关题目时,便可以快速解答.
(完)

