含砂热油管道温度与流速双耦合流态冲蚀规律对比分析

刘宏达， 陈一鸣， 杜胜男，2， 王卫强

(1.辽宁石油化工大学石油天然气工程学院， 辽宁 抚顺 113001；2.宁波工程学院机械与汽车工程学院， 浙江 宁波 315211)

0 前 言

随着原油勘探及开采量的不断增加，管道输送已逐渐成为原油输送的重要方式。 采用管道输送原油时，往往会有一定量的砂粒伴随原油进入管道[1]，对管道内壁造成冲蚀[2]，严重时会使管道系统失效。 弯管作为输油管道系统最常见的组成部分，其冲蚀现象尤为明显[3，4]。

针对原油管输过程中的冲蚀问题，相关学者展开了广泛的研究。 在国内，丁矿等[5]采用Tulsa 大学冲蚀与腐蚀联合研究中心(E/CRC)提供的冲蚀模型，对固体颗粒的空间分布与颗粒对直角弯管的冲蚀磨损问题进行研究，预测出了管道发生最严重磨损的位置；Wu等[6]以弯管和突扩管为研究对象，得出弯管弯曲角度及突扩管突扩比的减小均会促进磨蚀的重要结论；邓志强等[7]运用Fluent 计算流体力学软件对原油管输进行仿真模拟，分析了在不同的流速、压力和固体颗粒浓度下管道的冲蚀程度。 在国外，由于API RP 14E－1991标准[8]在含砂条件下具有一定的局限性，Salama[9]考虑到多相流中砂粒对弯管冲蚀的影响，提出了一种新的替代方程，提高了冲蚀预测的准确性；McLaury 等[10]在Salama 模型的基础上考虑到流体与砂粒特性等因素对冲蚀的影响，提出了一个综合的多相流冲蚀预测模型，并用试验数据验证了模型的准确性；Mohyaldin等[11]将Salama 模型和直接冲击模型(DIM 模型)与计算流体动力学模型(CFD 模型)进行对比分析，证明了DIM 模型的准确性，并通过考虑黏度对冲蚀的影响进一步改进了Salama 模型的精度，对原油冲蚀现象的研究具有一定的指导意义；与此同时，Al-Khayat 等[12]开发了三维CFD 模型，采用3 种建模方法(Finnie 模型、E/CRC 模型和DNV 模型)对管壁的冲蚀磨损进行了评价，讨论了在不同参数作用下砂粒对管壁的冲蚀效果；Ya 等[13]采用ANSYS Fluent 动态计算软件模拟了砂粒对管道中90°碳钢弯头的影响，结果表明，随着颗粒质量流量的增加，冲蚀率呈指数增长；Yusof 等[14]应用Fluent 软件对轻质原油在弯管中的流动进行了分析，得到了冲蚀速率随着砂粒粒径、流速和弯径比变化的规律。

总体而言，国内外研究者们主要针对流体运动参数、砂粒特性[15]及管道的几何特性[16]等因素对冲蚀的影响进行研究，而对温度及流体流动性质等因素导致的冲蚀问题关注较少。 与普通原油相比，目前开采的稠油在标准状况下黏度更大，流动性更差。 本工作在考虑稠油流动性对温度的要求的基础上，对比低黏原油与稠油在不同输送温度及不同流动条件下存在的冲蚀问题，对在同一含砂状态下影响2 种原油冲蚀速率的2 类关键因素进行敏感性分析。

1 数学计算模型

1.1 低雷诺数k-ω 修正模型

稠油流态随温度变化幅度较小，且会出现过渡流区，为提高计算精度，采用标准的k-ω模型[17]，并对k-ω湍流模型进行低雷诺数修正，使之适用于雷诺数为2 000～4 000 的过渡状态，经过修正后的k-ω计算模型[18]为:

式中，t为时间，s；ui为第i个坐标的流速，m/s；xi、xj为多元函数中第i和第j个横坐标点；ρ为流体密度，kg/m3；k为湍动能，J；Γk代表k的有效扩散率，m/s；Gk表示由于平均速度梯度而产生的湍流动能，J；Yk为k的湍流扩散项， J ；μ为流体动力黏度，Pa·s；σk为k对应的湍流普朗特数；μt为湍流黏度，Pa·s；α*为湍流黏度系数；ω为湍流耗散率；考虑到α*会对低雷诺数校正造成影响从而抑制湍流黏度，故重新定义α*为[19]:

1.2 高雷诺数k-ε 模型

高雷诺数k-ε模型适用于雷诺数大于4 000，且同时受到重力场和温度场的共同影响下的情况。 当同时受到重力场和温度场的影响时，Fluent 中的k-ε模型需要考虑浮力对湍流产生的影响。 计算模型[20]为:

式中，xi为多元函数中第i个横坐标点；Gb为湍流动能，J；β为热膨胀系数，1/K；gi为重力在i方向上的分量，m/s2；μt为湍流黏度，Pa·s；Prt为湍流普朗特系数，0.85；T为流体温度，K；ρ为流体密度，kg/m3；P为压力，Pa。

受浮力影响的耗散程度由常数C3ε确定，计算式为:

式中，v为流体平行于重力方向的速度分量，m/s；u为流体垂直于重力方向的速度分量，m/s；根据模拟条件，流体流动方向与重力方向垂直，v＝0，此时C3ε＝0。

1.3 传热模型

考虑管内原油与管道壁面、原油内部与沙粒间的导热及对流换热，不考虑流体内部的化学反应吸放热影响，计算模型为:

1.4 冲击角模型

由于Fluent 默认冲蚀模型参数值仅代表壁面边界条件，不能反映壁面材料属性，为适应管内原油流动特性，Fluent 默认冲蚀模型为:

式中，ER为冲蚀速率，kg/(m2·s)；mp为砂粒的质量流量，kg/s；dp为砂粒直径，mm；C(dp) 为砂粒颗粒直径函数；N为最大砂粒数；B为布氏硬度，N/mm2，本研究中取值为120；fs为沙粒形状系数，本研究选取球形砂粒，为0.2；Aface为壁面面积，m2；υ′为沙粒相对流速，m/s；f(θ)为冲击角函数。

冲击角函数采用分段多项式函数，新的计算模型见式(12)，冲击角函数模型见图1。

图1 冲击角函数模型Fig.1 Impact angle function model

2 物理模型及边界

2.1 物性参数

为提高模拟准确性，对原油相关物性参数进行测量，以塔河油田所产原油为对象，利用RS300 型HAAK流变仪(夹具为40 mm 平行板与珀尔贴板)，对2 种原油的黏温特性进行测量，剪切速率10 /s，试验结果如图2 所示。

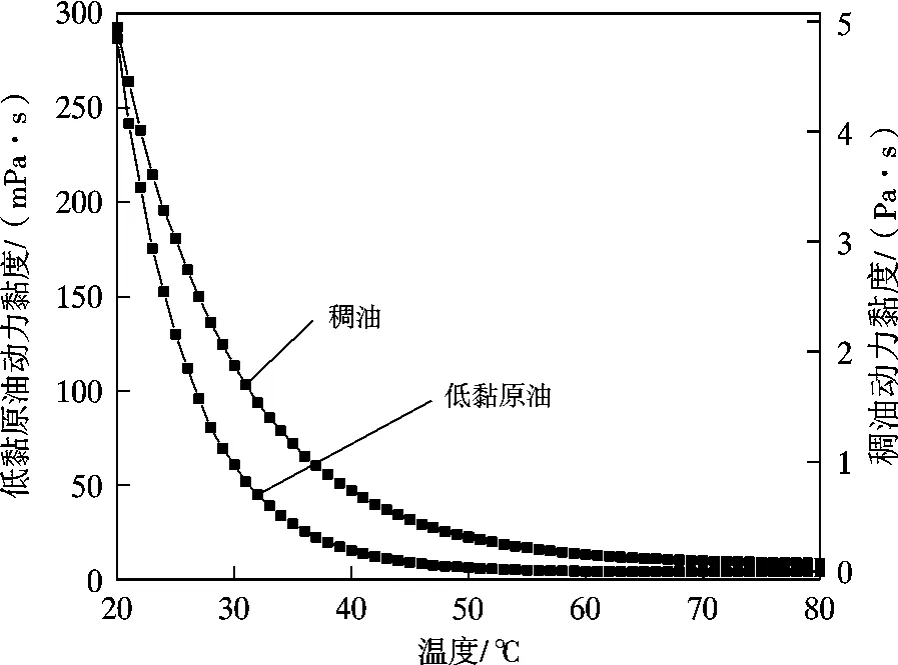
图2 稠油与低黏原油的黏温曲线Fig.2 Viscosity-temperature curves of heavy oil and low viscosity crude oil

经拟合后，稠油黏温关系为μ＝35 031.9e－0.099T＋65.1，低黏原油黏温关系为μ＝6 993.8e－0.16T＋3.98，稠油的平均密度为963.8 kg/m3，比热容为2 100 J/(kg·℃)，导热系数为0.13 W/(m·K)，凝固点为30 ～60 ℃；低黏原油的平均密度为828.9 kg/m3，比热容为1 560 J/(kg·℃)，导热系数为0.11 W/(m·K)，根据试验数据，对Fluent 内物质属性进行UDF(用户自定义函数)耦合定义；砂粒材料选取管线中常见的石英砂，其密度为2 650 kg/m3，比热容为920 J/(kg·℃)，颗粒粒径为0.1 mm，质量流率为0.01 kg/s。

2.2 几何模型与网格

模拟以油田集油管网某主管为对象，管道为X80碳钢，管径DN250.0 mm，外径273.0 mm，壁厚6.5 mm，工作压力3 MPa，为保证流体充分流动并抑制出口管段发生回流现象，设置进出口管长均为10D；整体计算域网格采用六面体单元进行划分，并在近壁面进行表面网格细化，弯管处局部加密，以提高模型的计算精度，模型网格数量为260 144，无关性检验表明，随网格数量增加，计算结果不再发生明显变化，其无关性检验曲线如图3 所示，三维模型如图4 所示。

图3 无关性检验曲线Fig.3 Independence test curve

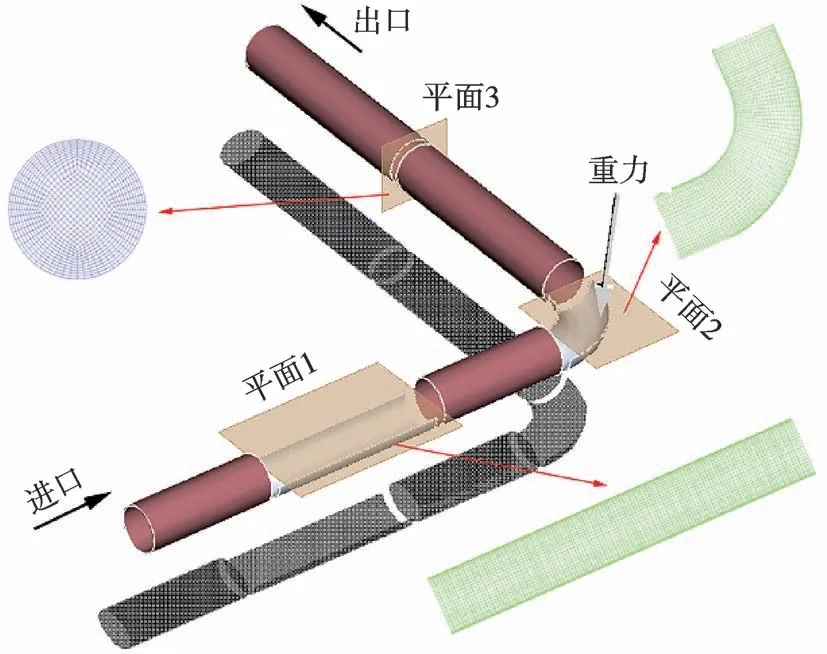
图4 三维模型Fig.4 3D Model

2.3 模型假设及边界条件

由于热油管道外壁面存在涂层及保温层，管壁与外界换热量较少，热交换集中于流体内部与壁面之间，换热形式以热传导为主，不考虑热对流，且只考虑流体内部温度变化，不计算管壁及保温层内部温度变化，因此，管壁热力边界采用只对内部壁面进行耦合的薄壁结构，以减少热扩散过程的计算量，热油管道薄壁结构如图5 所示。

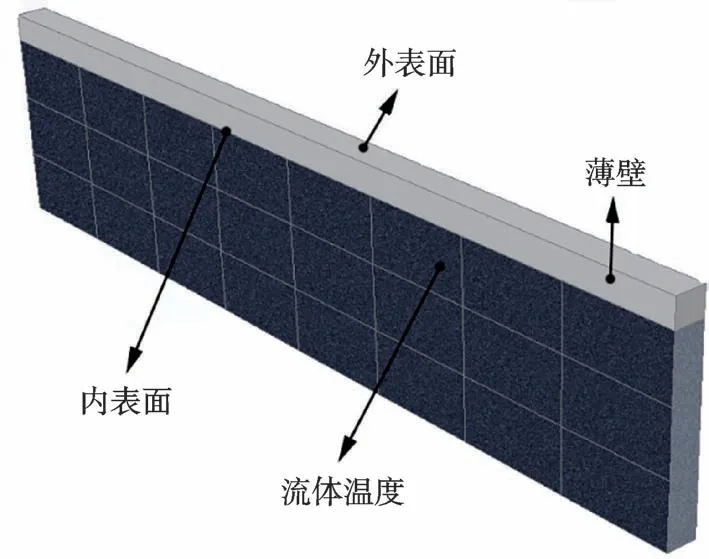
图5 热油管道薄壁结构Fig.5 Thin wall structure of hot oil pipeline

传热过程中仅考虑原油流动中所产生的黏性热及浮力影响，不考虑温度变化对原油密度的影响；由于连续相密度小于砂粒且砂粒直径较大，主要考虑影响砂粒运动轨迹的自身重力及曳力，忽略附加质量力、布朗力及Saffman 升力等；模型采用二阶迎风格式，Simple算法求解，离散相及流动边界条件如表1 所示[22]。

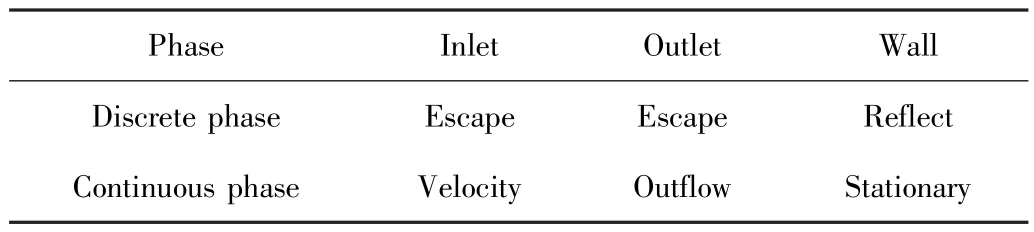
表1 边界条件Table 1 Boundary Conditions

3 结果与讨论

3.1 温度对弯管冲蚀的影响

温度是影响原油流动性的重要因素，由于稠油黏性较大，且受温度影响大，在输送时易在弯管外拱面形成黏性膜，对管壁起到一定的保护，弯头的严重冲蚀区域多呈现在内侧面；而低黏原油由于具有较低的黏度，更易在输送时直接对弯管外拱面造成冲蚀，冲蚀区域基本呈对称分布。 与此同时，与低黏原油相比，稠油的黏度与流动性也更易受到温度的影响。 因此，在稠油的集输过程中[23]，常常需要采用多种形式的伴热或加热输送方式，以降低原油的水力摩阻损失[24]。 为了分析不同温度下稠油和低黏原油管道中砂粒对弯管的冲蚀规律，分别对2 种含砂原油在不同温度下对管壁的冲蚀现象进行模拟。

3.1.1 不同温度下稠油冲蚀现象分析

在温度分别为40，60，80 ℃，入口流速为1.0 m/s，砂粒固体颗粒粒径为0.1 mm，质量流率为0.01 kg/s 的模拟条件下，含砂稠油对弯管内壁面的冲蚀情况如图6所示。

图6 不同温度下含砂稠油冲蚀分布Fig.6 Erosion distribution of heavy oil containing sand at different temperatures

由图6 可知，含砂稠油对管壁的冲蚀区域主要集中在弯管弯头的底部和内拱面，且冲蚀区域分布不均匀，在低温时进出口直管段并没有出现明显的冲蚀区域，随着温度的升高，弯管内弧面区的冲蚀面积逐渐 扩大。

为进一步明确温度对含砂稠油冲蚀速率的影响，对多组温度条件下的冲蚀速率进行了计算。 图7 为不同温度下含砂稠油的参数变化。 图7 表明，随着温度的上升，弯管内的冲蚀速率均呈现增长趋势。 不同流速条件下，冲蚀速率开始出现增长的初始温度不同，原油流速越高，冲蚀速率开始增加时所对应的温度越低。

图7 不同温度下含砂稠油的参数变化Fig.7 Parameter changes of heavy oil containing sand at different temperatures

此外，温度的升高使得不同流速条件下的原油经历了多个流动状态。 对于流速相对较高的原油(1.5，2.0 m/s)，温度的升高导致雷诺数增长较快，2 种流速的稠油分别约在64 ℃和71 ℃时进入湍流状态，同时冲蚀速率增长迅速。 对于流速相对较低的原油(0.5，1.0 m/s)，随温度的升高，其流动状态主要集中在层流及湍流过渡区域，冲蚀速率增长较缓慢。 可见，稠油冲蚀速率的变化与其雷诺数之间具有一定相关性。

3.1.2 不同温度下低黏原油冲蚀现象分析

在温度分别为40，60，80 ℃，入口流速为1.0 m/s，固体颗粒粒径为0.1 mm，质量流率为0.01 kg/s 的模拟条件下，含砂低黏原油对弯管内壁面的冲蚀情况如图8所示。

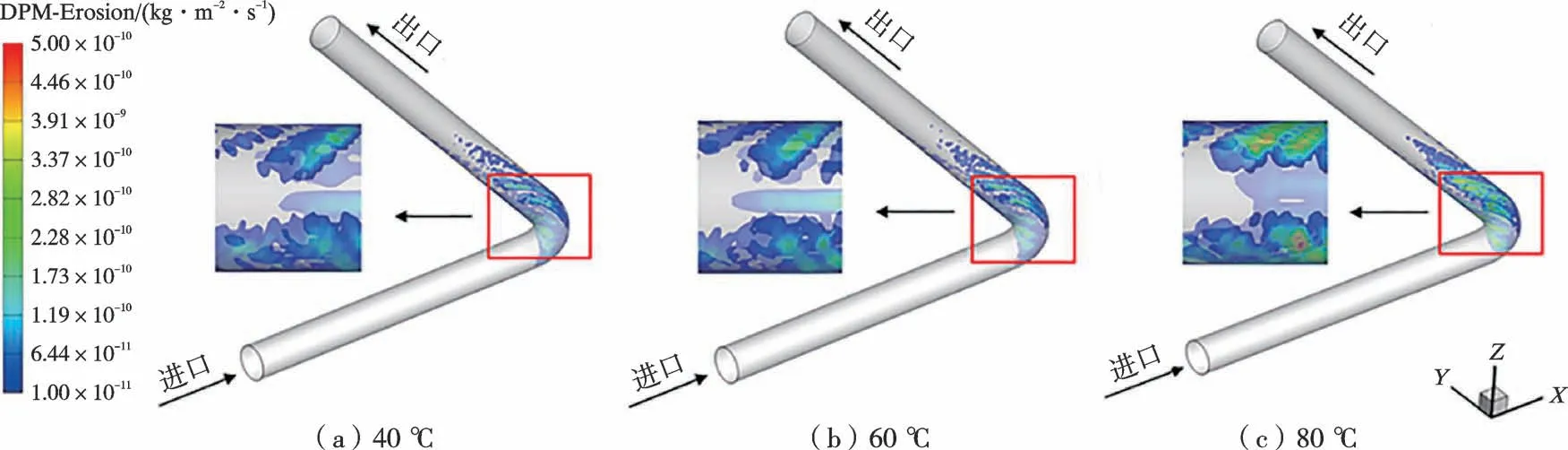
图8 不同温度下含砂低黏原油冲蚀分布Fig.8 Erosion distribution of low viscosity crude oil containing sand at different temperatures

与图6 稠油在弯管处形成的冲蚀相比，低黏原油冲蚀区域面积受温度的影响较小。 从图8 可以看出，在原油温度为40，60，80 ℃的条件下，其冲蚀覆盖区域未发生明显变化，但原油对管壁的冲蚀强度有所增加。

图9 为不同温度下含砂低黏原油的参数变化。 随着温度的上升，其冲蚀速率变化规律与稠油类似，总体呈上升趋势。 与稠油相比，在原油流速较低的情况下(0.5，1.0 m/s)，虽然含砂低黏原油的流动状态随温度的升高进入了湍流区，如图9b，但其冲蚀速率并没有出现较为明显的增加，如图9a。 而在流速较高的情况下(1.5，2.0 m/s)，含砂低黏原油的冲蚀速率随温度的升高在过渡区出现了较大幅度的波动。 随着原油进入湍流区，其冲蚀速率的增长逐渐放缓。

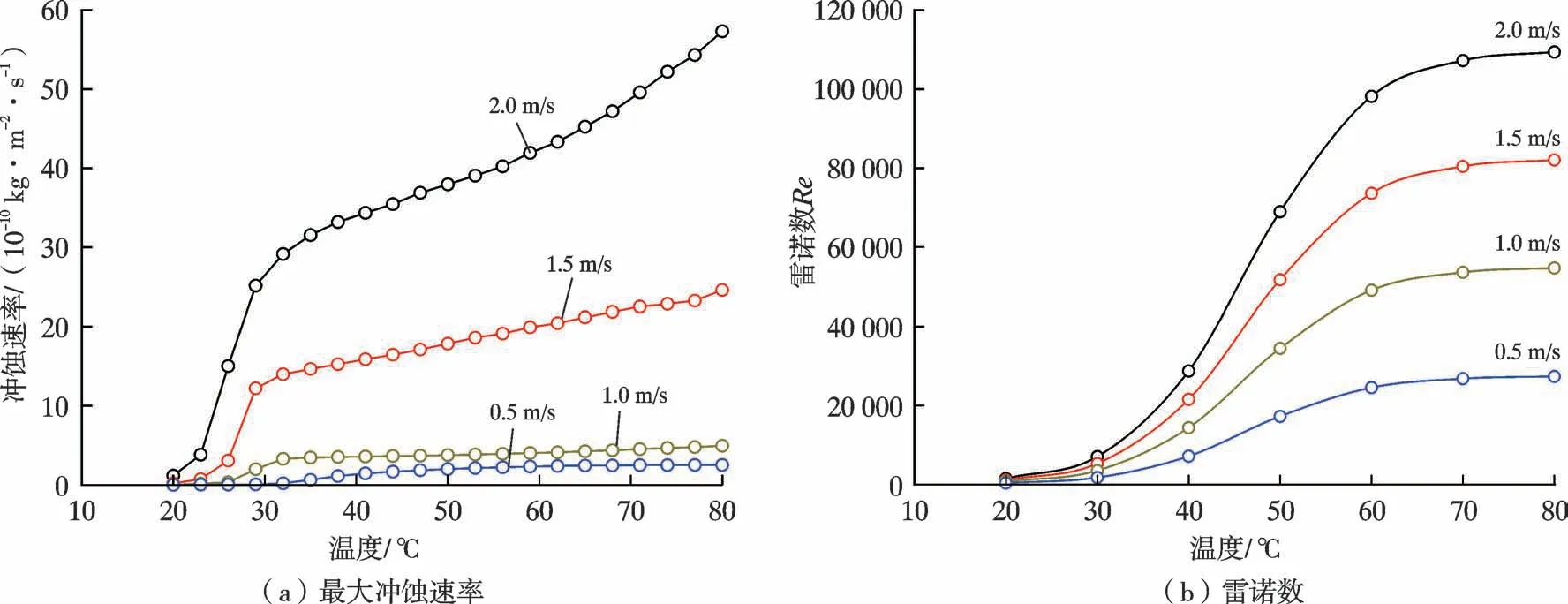
图9 不同温度下含砂低黏原油的参数变化Fig.9 Parameter changes of low viscosity crude oil containing sand at different temperatures

3.2 流速对弯管冲蚀的影响

根据温度对2 种原油冲蚀速率的影响结果，在保证2 种原油温度相同的情况下，对流速与冲蚀速率的关系进行模拟计算。 模拟环境温度25 ℃，固体颗粒粒径0.1 mm，质量流率0.01 kg/s，计算结果如图10 所示。由图10 可知，在温度相对较高的情况下(40，60，80℃)，稠油与低黏原油均随流速的增加逐渐进入湍流区，2 种原油对弯管的冲蚀速率也随流速的增加呈现出增长趋势。 且低黏原油的增长幅度明显高于稠油。 在温度较低的情况下(20 ℃)，2 种原油随流速的增加而处于层流及低雷诺数过渡区，其与弯管间不会出现明显的冲蚀作用，冲蚀速率基本为0。

3.3 恒定湍流雷诺数下温度及流速对弯管冲蚀的影响

温度及流速对冲蚀速率的计算结果表明，在湍流状态下，2 种原油的温度与流速的增加都会导致冲蚀速率的增大。 为保证2 种原油均处于湍流状态且符合实际需要，经计算，当雷诺数为5 000 时满足稠油实际输送的温度要求。 因此在维持雷诺数为5 000 不变的情况下，对温度与流速2 个因素对冲蚀速率的影响程度 进行比较，其结果如图11 所示。

图11 最大冲蚀速率与温度和流速的关系Fig.11 Relationship between maximum erosion rate and temperature and flow velocity

图11 显示了在雷诺数保持不变的情况下(Re＝5 000)，2 种原油的流速由1.0 m/s 增加2.0 m/s，且温度逐渐下降过程中冲蚀速率的变化情况。 对比之前研究中温度与流速对原油湍流状态下的冲蚀作用规律发现，在相同的湍流状态下，相比于温度因素，原油流速在对冲蚀速率的影响中占主导作用。 即使在温度下降的情况下，流速的增加依旧会提高原油对弯管的冲蚀作用。 从图11 中可以看出，这种影响在稠油管道中比在低黏原油管道中更加显著。

4 结 论

在温度与流速耦合流态的影响下，通过对比2 种含砂原油冲蚀速率的变化规律，得到以下结论:

(1)稠油和低黏原油油温的上升均会提高其对弯管的冲蚀速率。 其中，在温度升高的情况下，稠油的冲蚀速率与其自身雷诺数的增长趋势具有一致性；低黏原油冲蚀速率则受流态变化影响，在过渡区时冲蚀速率与其自身雷诺数的增长趋势存在较大波动；

(2)在油温较低的条件下，2 种原油对弯管的冲蚀速率随流速的增加变化较小；随着油温的增加，2 种原油冲蚀速率随流速的增加逐渐增大。 且在相同温度条件下，低黏原油冲蚀速率的增长幅度要大于稠油；

(3)在相同湍流状态下，2 种原油流速变化在冲蚀过程中起主导作用，油温的降低并不能有效缓解弯管处的冲蚀现象。