基于深度学习的时间角度控制制导律

刘子超, 王 江, 何绍溟,3,*

(1. 北京理工大学宇航学院, 北京 100081; 2. 北京理工大学中国-阿联酋智能无人系统“一带一路”联合实验室, 北京 100081; 3. 北京理工大学长三角研究院(嘉兴), 浙江 嘉兴 314019)

0 引 言

随着反导防空技术的发展,重要战略目标的防御能力普遍提升,使导弹面临严峻的拦截威胁。多弹协同攻击能够使反导系统在短时间内达到饱和,是突破敌方防空反导系统的一种有效手段[1]。为了取得更佳的毁伤效果,一般还需要导弹以一定的角度命中目标,因此一些制导律在实现飞行时间控制的同时引入了角度约束[2]。研究飞行时间和攻击角度控制制导律具有重要的现实意义,本文研究了一种基于深度学习的时间角度控制制导律(impact time and angle control guidance, ITACG)。

现有的ITACG大部分需要精确预测剩余飞行时间。李斌等[3]将时间误差和角度误差视为跟踪误差,然后基于最优误差动力学推导了飞行时间误差反馈制导指令;Chen等[4]推导了最优角度控制制导律的剩余飞行时间,使用闭环反馈控制的形式实现时间角度控制,相对于其他开环制导律具有更好的鲁棒性;文献[5-6]构造了视线角多项式,生成满足角度约束的弹道轨迹,推导了轨迹长度,通过轨迹跟踪实现时间角度控制制导;Wang等[7]考虑弹间存在通信链,基于一致性算法控制多弹的剩余飞行时间达到一致,该方法的优势在于不要求所有导弹具有相同的飞行速度。文献[8-11]将时间角度控制制导律推广至三维场景。上述制导律在设计阶段均依赖常值速度假设,应用于实际环境时制导性能可能变差。Zhang等[12]考虑速度时变场景,构建速度剖面,然后使用加权平均加速度对速度剖面近似线性化,一定程度上提高了剩余飞行时间的预测精度,但是需要一定的积分运算,计算量较大。

由于剩余飞行时间的预测精度会对制导性能造成一定影响,因此也有学者从其他技术途径开展研究。Harl等[13]设计了视线角的变化规律,从而生成满足时间角度约束的视线角速率曲线,并且使用滑模制导律跟踪曲线;吴放等[14]在Harl的基础上改进了视线角多项式,更易于工程实现;Hu等[15]使用伪目标将弹道分为两段,根据期望飞行时间确定伪目标的位置,采用滑模制导与比例导引实现时间角度控制;Chen等[16]将时间约束和角度约束转化为状态约束,使用滑模制导律实现状态控制;Hou等[17]通过滑模制导律实现了针对常值机动目标的时间角度控制制导;Wang等[18]通过滑模制导律进一步研究了目标执行正弦机动的时间角度控制制导;Li等[19]将滑模制导律推广至三维场景;Wang等[20]通过模型预测控制实现时间角度控制;Zhu等[21]设计了一种确定的机动策略,根据期望飞行时间执行额外机动;Yan等[22]基于空间几何关系推导了三维时间角度制导律;Kim等[23]设计了一种多项式制导方法,在生成多项式曲线时首先引入角度约束,通过调节多项式参数调节轨迹长度,从而实现时间控制;Surve等[24]设计视线角多项式实现时间角度控制;Deng等[25]使用迭代计算求解带有时间角度约束的最优控制问题;杨秀霞等[26]以两段圆弧作为飞行轨迹实现时间角度控制,该制导律工程应用简单,但是机动幅度较大,不适用于导弹平台。

随着深度学习技术日趋成熟,近年来学者们开始探索将深度学习技术应用于制导领域[27]。黄等[28]提出了一种两阶段控制策略,第一阶段使用反向传播神经网络预测剩余飞行时间,当剩余飞行时间满足期望时间时进入第二阶段,使用角度控制制导律飞行。该方法没有考虑速度变化;Liu等[29]基于速度时变模型实现了飞行时间控制,但没有考虑角度约束。

本文基于预测校正制导思想,将时间角度协同制导律的设计转化为对飞行时间误差和角度误差的控制问题。首先使用最优角度控制制导律控制角度误差,然后以最优角度控制制导律为基础,通过深度学习计算飞行时间误差,设计校正制导律,使飞行时间误差收敛。本文的主要贡献如下:① 使用深度学习提高了预测校正制导的计算效率;② 设计前馈环节融合了理论模型与深度学习方法,改善了神经网络的训练效果;③ 引入了导弹的动力学模型,更接近实际工程应用环境,具有一定的实用价值。

1 问题描述

针对导弹攻击固定目标的时间角度控制问题,建立如图1所示的弹目相对运动的模型。

图1 弹目相对运动关系

图1中,R表示弹目相对距离,λ表示弹目视线角,v表示导弹速度,θ表示导弹的弹道倾角,η表示速度方向误差角,L表示弹道轨迹长度,FL、FD、FG分别表示升力、阻力与重力。

导弹的动力学方程为

(1)

式中:x表示导弹在平面中的横向位置;y表示导弹的高度;m为导弹质量;

升力、阻力与重力的计算公式为

(2)

式中:CL表示升力系数;CD表示阻力系数;g表示重力加速度;S表示导弹的参考面积;Q表示动压,形式为

(3)

式中:ρ为大气密度,使用北半球标准大气模型计算。

弹目相对运动方程为

(4)

导弹终端约束为

(5)

式中:(xf,yf)为导弹的目标位置;td为期望的飞行时间;λd为期望的攻击角度。

2 ITACG框架

本文设计的ITACG的框架如图2所示,图中tgo表示导弹的剩余飞行时间。该制导律以预测校正制导框架为基础,在最优角度控制制导律的基础上增加飞行时间误差反馈项,使用深度学习方法精确预测最优角度控制制导律的剩余飞行时间,通过校正制导律使导弹的飞行时间误差收敛至0附近,最终实现飞行时间和攻击角度的共同控制。

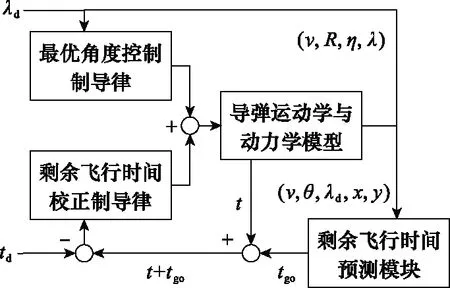
图2 基于深度学习的ITACG框架

预测模块以导弹的飞行状态以及期望攻击角度为输入,以剩余飞行时间为输出。现有的预测校正制导中,预测模块普遍需要通过数值积分预测导弹的终端状态,计算量较大[27]。基于深度学习的剩余飞行时间预测模块从样本数据中学习输入输出之间的复杂映射关系,使用少量的运算即可获得精确的预测结果,因此能够显著提高算法的实时性。

校正模块使用比例控制算法,根据剩余飞行时间误差计算校正制导指令。由于预测模块使用的样本分布具有马尔可夫性,并且校正模块生成的校正指令使预测误差逐渐收敛,因此基于深度学习的ITACG对历史误差不敏感,能够更好地适应导弹模型偏差与环境扰动,鲁棒性和抗扰性较好。

3 剩余飞行时间预测

最优角度控制制导律[30]可表示为

(6)

式中:η=λ-θ;ηe=λd-λ。剩余飞行时间tgo定义[18]为

(7)

式中:弹道轨迹长度L为

(8)

若飞行速度v为常值,最优角度控制制导律的剩余飞行时间tgo的理论值[3]为

(9)

常值速度假设将剩余飞行时间预测问题转化为剩余轨迹长度预测问题,因此式(9)在常值速度模型具有较高的预测精度。但是考虑速度变化后,在某些场景预测精度可能会显著下降。

以x=-20 km,y=20 km,v=210 m/s,θ=0°为初始条件,使用式(6)的制导律并且以λd=90°为终端角度约束攻击位于原点处的固定目标,采用常值速度模型与考虑速度变化的模型分别进行仿真,并使用式(9)预测剩余飞行时间,预测结果如图3和图4所示。在常值速度模型下,式(9)的预测精度较高,但是在引入导弹的动力学模型后,该公式的预测误差明显增大。

图3 基于常值速度模型的剩余飞行时间预测结果

图4 基于速度时变模型的剩余飞行时间预测结果

在实际应用中,式(9)的预测误差可能导致制导性能下降,甚至任务失败。因此,在对最优角度控制制导律进行剩余飞行时间估算时,不仅要考虑过载指令对弹道曲率的影响,还应当考虑气动力对飞行速度的影响。然而,在引入气动力后,导弹的动力学方程求解难度较大,一般无法使用解析方法求解。

由式(7)可见,tgo是飞行速度v和弹道长度L的函数,弹道长度受弹道曲率θ与剩余航程x影响。按照式(6)的制导律攻击目标时,弹道曲率的变化规律由v,R,θ,λ,λd确定。注意到v的动力学主要受到气动力的影响,而气动力中的大气密度ρ又能够表示为高度y的函数。由于目标静止,弹目相对几何关系(R,λ)与导弹在惯性空间的位置(x,y)等价。因此,可将tgo表示为

tgo=f(v,θ,λd,x,y)

(10)

使用深度学习方法可以拟合式(10)表示的映射关系,但是由于tgo的值域范围较大,可能需要更多的训练步数,预测精度也有可能降低。为了进一步提高训练效率与训练精度,将tgo表示为

(11)

对tgo的估计由两部分组成:基于模型的理论值与基于数据的拟合值Δt。Δt是理论模型对剩余飞行时间的估计误差,使用深度神经网络拟合Δt时,基于模型的理论值能够使目标值域缩小,提高神经网络训练速度,同时改善神经网络的预测精度。剩余飞行时间预测模块如图5所示。

图5 剩余飞行时间预测模块

本文使用的深度神经网络为具有10个隐层的残差神经网络[31],每个隐层包含100个神经元。残差神经网络解决了网络深度的退化问题,能够进一步提高网络性能。深度神经网络训练数据来源于蒙特卡罗仿真飞行实验,仿真飞行使用带有气动力的模型。在仿真飞行的初始阶段,除了随机给定初始位置(x,y)与初始速度(v,θ),同时随机给定期望的攻击角度λd。当样本采集完成后,对深度神经网络进行训练。

将深度神经网络的网络参数定义为β,定义损失函数为网络参数β的函数为

(12)

(13)

式中:αβ为学习率。

4 制导律设计

ITACG的制导指令表示为

aM=aOA+aIT

(14)

式中:aIT为飞行时间控制制导指令项。

定义εt为飞行时间误差:

εt=td-tf=td-(t+tgo)

(15)

在设计校正制导指令时,可以假设v为常值。忽略飞行速度变化可能导致校正指令无法满足最优性,但是在引入精确的预测环节后,校正指令能够使εt正确地收敛。引入式(9)对飞行时间tf=t+tgo求导

(16)

(17)

由于式(17)不显含控制指令,使用飞行时间控制制导指令项简化弹道倾角的动力学为

(18)

将式(15)、式(18)代入式(17),可得εt的导数为

(19)

忽略式(19)的高阶项,将εt的导数简化为

(20)

设计期望误差动力学为

(21)

式中:K>0为比例系数,K值越大,εt的收敛速度越快。

求解式(21)的微分方程可得εt的解为

εt=ε0e-Kt

(22)

式中:ε0为误差的初值。

按照式(21)的期望误差动力学可以令误差按指数函数形式迅速收敛,将式(20)代入式(21),得到飞行时间控制制导指令项aIT为

(23)

将式(6)、式(23)代入式(14),可得ITACG为

(24)

当εt收敛为零后,式(24)的ITACG退化为角度控制制导律。

5 仿真分析

5.1 剩余飞行时间预测模块仿真分析

导弹气动系数可近似表示为

(25)

表1 导弹气动系数

导弹攻角在飞行过程中取平衡攻角,计算公式为

(26)

导弹初始飞行状态的取值范围如表2所示。弹体的参考面积S=0.05 m2,重力加速度g=9.81 m/s2,攻角取值范围限制于区间[-15°,15°]内。

表2 导弹初始飞行状态

运行1 000次蒙特卡罗仿真实验,共获得19 407 425组样本,将样本的80%作为训练集,剩余20%作为测试集,设置学习率αβ=0.001,使用训练集对神经网络进行训练。

使用测试集测试训练好的神经网络,测试结果如图6所示。由图可见本文设计的预测模块实现了较高精度的剩余飞行时间预测,预测误差不大于1 s。

图6 剩余飞行时间预测模块的测试结果

5.2 时间角度协同制导律仿真分析

本节将式(24)中的参数K设置为0.1,以x0=-10 km,y0=10 km,v0=300 m/s,θ0=0°为初始状态开展一系列仿真实验。图7对比了基于精确tgo的ITACG与基于式(9)解析tgo的ITACG,由图可见基于解析tgo的ITACG脱靶,这是因为式(9)的推导过程引入了常值速度假设,预测误差增大,导致制导指令不合理。

图7 两种不同ITACG的仿真结果对比

设定一系列的场景对本文提出的ITACG进行仿真,首先设置不同的期望飞行时间和相同的期望攻击角度,期望飞行时间分别设置为td=60 s,80 s,100 s,期望攻击角度设置为λd=90°,仿真结果如图8所示。

图8 不同期望飞行时间的制导性能

然后设置不同的期望攻击角度和相同的期望飞行时间,期望攻击角度分别设置为λd=30°,60°,90°,期望飞行时间设置为td=60 s,仿真结果如图9所示。

图9 不同期望攻击角度的制导性能

从图8和图9可见,本文设计的制导方法能够使导弹在命中目标的同时满足飞行时间约束与攻击角度约束,验证了本文设计的ITACG的有效性。

为了进一步说明本文设计的ITACG相对现有制导律的优势,使用文献[3-4]设计的ITACG与本文提出的ITACG进行对比。期望攻击角度设置为λd=90°,期望飞行时间设置为td=60 s,仿真结果如图10所示,导弹命中目标时的性能如表3所示。

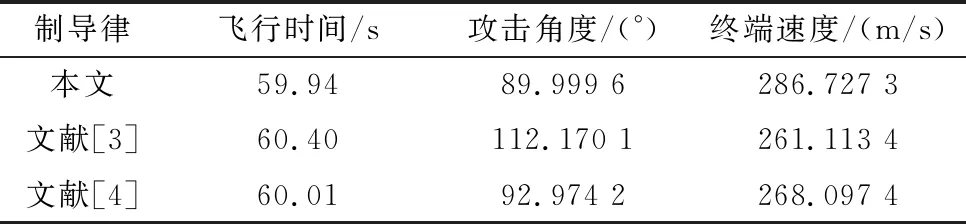
表3 3种不同ITACG的性能

图10 3种不同ITACG的仿真结果

从图10和表3中可以看出,3种制导律都能按照期望的飞行时间命中目标,但是文献[3-4]的攻击角度误差较大。导弹使用本文的ITACG命中目标时,相对于其他两种ITACG具有更大的终端速度与终端动能,在实际应用时具有更好的毁伤效果。

5.3 时间角度协同制导律仿真分析

使用蒙特卡罗仿真实验测试ITACG在不同状况下的制导性能,飞行时间与攻击角度分别从[60 s,100 s]、[30°,90°]中随机选取。重复1 000次实验,绘制各次实验的飞行时间误差εt与攻击角度误差εa如图11所示。从图11可见,本文的ITACG在不同初始情况与目标条件下均能以较小的误差命中目标。

图11 蒙特卡罗仿真实验结果

6 结束语

本文针对飞行时间和攻击角度约束,提出了一种基于深度学习的ITACG,该制导律引入了导弹的动力学模型,以预测校正制导框架为基础,应用深度学习方法预测剩余飞行时间,实现时间角度控制制导。在预测剩余飞行时间时,设计前馈环节融合了理论模型与数值方法,改善了神经网络的训练效果。仿真结果表明,相对于传统的飞行时间估计方法,深度学习能够实现更加精确的剩余飞行时间估计,而更精确的估计结果能够显著改善时间角度控制制导律在实际场景中的性能。下一步的研究方向包括针对机动目标的时间角度控制制导,以及考虑能量最优性的校正制导指令设计。