基于匈牙利-模拟退火算法的多阶段武器目标分配方法

常雪凝, 石建迈, 陈 超, 黄金才

(国防科技大学系统工程学院, 湖南 长沙 410003)

0 引 言

随着自控技术、信息技术以及人工智能等技术的发展,以导弹为代表的精确制导武器装备朝着精确化、智能化的方向变革,推动了信息化、智能化、无人化战争的进程[1-2]。在俄罗斯攻打乌克兰的战役中,远程精确制导武器在战场上发挥了重要的作用。精确制导武器作为一种典型的信息化武器[3],可以远距离快速识别、命中并摧毁敌方目标,将军事冲突限制在一个特定的区域,大大减少了战场人员伤亡和财产损失,是快速摧毁敌军重要设施、赢得局部作战胜利的主要方式。然而,远程精确制导武器也存在一些短板,首先是成本极高,从装备到升级以及武器本身的花费都远超常规武器系统[4]。其次是武器发射平台数量有限,受到成本、技术和人员等限制,远程精确制导系统的发射平台数量有限,因此同一波次发射的武器数量也是有限的。面对大量需要拦截和打击的目标群时,需要将作战过程合理划分为多个阶段,利用有限的发射平台将武器分配到目标,实现最佳的打击效果。

为了提高远程精确打击的作战效益,需要在改进武器装备的同时,对智能指挥作战系统,尤其是武器分配方法进行重点研究[5]。武器目标分配(weapon target assignment, WTA)问题是军事运筹领域的重要研究方向之一,是解决如何将多种作战武器,分配给多个打击目标,来最优地实现指挥员的作战意图,也是指挥控制自动化、智能化需要解决的关键问题之一。作为WTA问题的一种重要扩展方向,多阶段WTA(multi-stage WTA, MS-WTA)是在有限的武器通道和武器数量的约束下,对多元立体的打击目标加以评估,依据重要性与紧急程度划分阶段,通过规划各阶段打击目标清单缓解同波次武器攻击的压力,快速制定WTA方案。文献[6]认为在作战规划过程中,“能力需求”会改变,WTA效益必然也相应发生变化。因此,研究高实时性的MS-WTA方法,已经成为战场火力分配研究的重点。

Flood[7]在普林斯顿大学线性规划会议上首次提出目标分配模型,在军事运筹领域引起了广泛关注与研究。在WTA数学模型方面,Manne[8]首次建立了混合整数非线性规划模型。Lloyd等[9]证明了WTA是非确定性多项式(nondeterministic polynomially, NP-hard)的,即在多项式时间内是不可解的。因此,在不对模型进行转化的情况下,很难做到使用精确求解技术来求解WTA大规模算例。Dirik等[10]提出了一种两阶段混合线性规划建模方法来解决战斗机WTA问题。Han等[11]建立了三阶段(防御方-攻击方-防御方)的完全信息零和博弈模型。Peng等[12]基于目标毁伤概率区间和时间窗约束,提出了一种新的协同空战动态WTA多目标整数优化模型。陆一平等[13]通过限定对目标分配武器的数量来降低整数线性规划模型的维数,提高问题的求解效率。针对多个武器拦截多个目标问题,Stieber等[14]将该问题近似为带移动目标的多旅行商问题,建立了一个整数线性规划模型。Guo等[15]则提出使用固定和自适应的分组策略来确保每个目标都能分配到适当的拦截资源,并使用罚函数将多约束优化转化为无约束优化问题。Lu等[16]将WTA问题转化为一个具有二进制列的线性整数规划模型,实现了大规模WTA的求解。此外,更复杂的、更切合实际应用的WTA场景也被考虑。Xin等[17-19]提出了传感器协同分配的WTA问题,Li等[20-21]提出使用多目标进化算法(multi-objective evolutionary algorithm, MOEA)来解决多目标WTA问题。

WTA问题是一个多参数、多约束的NP-complete问题,解空间往往是不可微、不连续以及高度非线性的。目前,WTA的求解方法可以分为两类,第一类使用精确求解技术,如分支定界法、拉格朗日松弛方法和匈牙利方法等[22-24],直接求解混合整数非线性形式的WTA问题。Kline等[23]设计了一种基于深度优先搜索的分支定界算法,解决了较小规模的非线性整数规划WTA问题。Chopra等[25-26]在匈牙利方法的基础上提出“加边补零”的扩增方法来统一效率矩阵,实现了小规模WTA问题的快速求解。郭斐然等[27]提出使用层次分析技术和匈牙利算法解决了不同类型部件和装备体系的配对问题。为了找到大规模WTA的精确解,可通过一些假设和模型转换适当地简化问题。例如,Lu等[16]建立了一种线性规划WTA模型,采用列生成和分支定界结合的方法有效解决了大规模WTA问题。第二类求解技术是基于启发式方法,通过适当降低解的质量来实现大规模WTA问题的快速求解。Lee等[28]提出将领域知识融入遗传算法的交叉和变异过程,用于求解中等规模的WTA问题。Xin等[29]设计了一种基于规则的启发式构造算法求解动态WTA问题,通过动态验证约束是否饱和来生成可行解。Liang等[30]实现了自适应混沌并行克隆选择算法求解舰艇编队防空WTA问题。Sonuc等[31]提出了并行模拟退火算法求解大规模WTA的问题。Zhang等[19]建立了一种基于滚动时域分解策略模型,设计了一种基于统计边际收益的启发式算法,实现了基于资产的动态WTA问题的求解。

综上所述,WTA问题经过几十年的发展,在模型、求解算法以及应用场景方面都取得了大量研究成果,以静态WTA和动态WTA为基础不断发展,但是现有的研究很少关注MS-WTA问题。在实际的应用中,由于武器发射平台不足以及武器存在转火时间的原因,无法一次性完成对所有目标的打击任务,必须将作战划分为多个阶段,制定出整体效益最大化的火力打击计划。此外,对于大规模的WTA问题,大多数精确算法不能在有效时间给出解决方案或者解决方案质量较低[32]。启发式方法虽然通过降低解的质量来实现快速求解,但是不可避免地出现过早收敛、解的质量稳定性差等问题。因此,在精确打击的背景下,本文立足于一般形式的WTA问题,考虑阶段间分配方案的相互影响,提出一种启发式和精确式算法结合的MS-WTA算法,最大化整体打击效能。

1 问题分析与建模

MS-WTA问题属于经典WTA问题的扩展。考虑到远程精确制导装备在单波次攻击中武器发射数量有限,当目标数量庞大时,只有主动地将打击过程分成多个阶段来分配武器,才能发挥精导武器的最大作战效益。MS-WTA问题假定需要在较短时间内完成对敌军的n个目标的摧毁任务,目标j的威胁程度记为Vj,其中j∈N={1,2,…,n};现有武器发射平台M个,每个平台在一个阶段至多可以发射1个武器;整个打击过程划分为w个阶段,一枚武器仅能攻击一个目标。其中,建模过程中采用的参数与变量如表1所示。

表1 参数与变量符号说明

在精确制导武器多阶段打击的背景下,给出以下设定。

(1) 每一个目标仅被一枚武器的攻击,打击目标体积大或者防御性过强时,通过增设虚拟目标来拆分原目标以及相关参数。

(2) 一个武器在一个阶段只能攻击一个目标,并且武器在完成发射之后,仅追踪与打击预设的目标。

对于一个初始目标集合N,需要经过信息评估后将所有目标分配到s个集合,任意一个阶段的待打击目标集合用Nt表示。在本问题中,Nt的目标类型和数量是可变的,以目标j和目标k为例(其中j∈Nt,k∈Nt-1),当目标j经过评估是可松弛的,即松驰系数(relaxation coefficient, RC)为1,那么其可以向相邻的后续阶段调整,与相邻的后续阶段的某个目标k交换打击次序;阶段调整完成后,目标j被标记为不可松弛的,并且此时j∈Nt-1。相应地,目标k向前一个阶段调整,且无论之前评估信息如何,由于当前所属阶段处于较早的攻击波次,可以对其进行可松弛标记,即RC=1,此时k∈Nt。阶段调整完成后,目标的打击阶段被确定,可以在此基础上进行WTA以找到局部最优解。

从攻击方角度,旨在降低敌方目标的威胁程度,当武器被分配给目标并完成打击任务时,敌方的总体威胁越小越好。因此,MS-WTA问题以最小化敌方目标的总体期望威胁值作为优化目标,计算统一效率矩阵,具体数学模型如下:

(1)

(2)

(3)

xtij∈{0,1}, ∀t∈S;i∈W;j∈N

(4)

模型中,式(1)为目标函数,目标威胁值将会根据武器毁伤概率大小非线性降低。式(2)～式(4)为约束条件,其中式(2)约束了在每一个攻击阶段,目标j只能被一个武器打击;式(3)约束了一个武器最多追踪并袭击一个目标。在式(2)和式(3)的约束下,每一个阶段发射的武器数量等于需要打击的目标数量。当所有目标的初始攻击阶段被确定下来,指挥员需要优化武器和目标之间的分配关系来实现作战效能的最大化,式(4)是0-1决策变量约束。

2 基于匈牙利-模拟退火的双层搜索算法

为了解决MS-WTA问题,基于匈牙利算法和模拟退火算法,设计了一种双层搜索算法,简称为匈牙利模拟退火(Hungarian simulated annealing, HSA)算法。首先,根据目标的重要性与紧急程度确定目标的初始攻击阶段,再利用精确制导武器典型打击场景中目标一对一精准打击情况下的应用特点,使用匈牙利算法计算MS-WTA问题的初始解。随后,在模拟退火算法框架下,调用阶段调整算子重新对目标的攻击波次进行调整,并再次调用匈牙利算法求解当前状态下的局部最优解,在退火降温过程中利用概率突跳重新对目标的攻击波次进行调整,重复循环这一过程,直至满足停止准则,得到高质量打击方案。基于HSA的双层搜索算法的主要流程如算法1所示。

算法 1 HSA算法步骤 1 参数初始化;步骤 2 基于一定的规则构造多阶段目标攻击初始序列F={F1,F2,…,Fs};步骤 3 在初始序列F的基础上,标记各目标松弛系数rj;步骤 4 调用匈牙利算法求解MS-WTA的局部最优解F*={F*1,F*2,…,F*s};步骤 5 计算目标函数值;步骤 6 在局部最优解F*的基础上,根据松弛系数调整准则改变目标打击阶段,构造新序列F;步骤 7 依据一定的概率准则更新RC值;步骤 8 重复步骤4和步骤5;步骤 9 调用模拟退火算法转到步骤6^步骤8;步骤 10 直至到达算法终止准则,解算出全局最优解。

2.1 RC调整准则

RC是调整目标打击阶段的重要数值标记,同时也能反映出目标重要性。目标j的RC记为rj,给予紧迫性强、优先级高的目标RC值为rj=0,反之为1。在后续的WTA过程中,RC值决定了该目标是否可以调整打击阶段以产生更优的打击方案。使用RC准则来调整打击阶段,需要遵循如下几条规则。

(1) 目标优先级越高,打击阶段越靠前

在预分配阶段,进行初始目标划分和标记时,目标的重要性越强,优先级越高,相应的初始打击阶段越靠前。对同波次目标来说,RC标记能反映出目标的相对重要性,rj=0代表目标处于重要而紧迫的地位。比如,敌方指挥机构和预警探测类目标(如雷达站)相对于防御工事和保障部队等具有更优先的打击次序,应当分配到较早的波次中,若两者可以在同一阶段被打击则可以通过RC值来标记相对重要性。

(2) 目标只能向相邻阶段进行调整

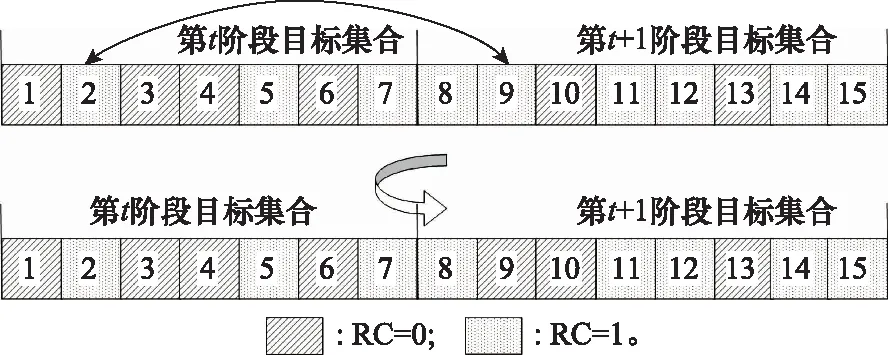
对当前目标进行阶段调整时,只能选择相邻的阶段进行改变。本文提出的算法每次以随机的方式选择相邻的任务集合,再以同进同出的方式交换两个目标的打击阶段。如图1所示,不允许交换第1和第3阶段的目标(对应图1序号③)。因为较早阶段的目标本身具有很强的优先级,跨阶段调整违背了“目标优先级越高,打击次序越靠前”的原则。

图1 RC更新

(3) RC值的更新方法

选定两个阶段的目标集合后,后续阶段的目标可以无条件向前一阶段迁移,迁移完成后RC值更新为1;但是对于前阶段目标,只有RC值为1时才可以向临近的后续阶段迁移,同时RC值更新为0,意味着尽管该目标在原先阶段优先级并不大,可以向后调整,但是仍然有很重要的地位,不允许继续向后续阶段继续调整。

2.2 HSA算法

2.2.1 匈牙利算法

WTA问题与传统运筹学中的指派问题有很多相似之处,当规定武器对目标实施一对一精准打击时,两者的数学模型拥有相似的形式,如式(1)～式(3)。匈牙利算法是Kuhn在1955年利用匈牙利数学家König提出的独立零元素定理构造求解方法,被认为是指派问题标准的解法,具有求解速度快、解的质量稳定的特点[23]。当武器和目标数量相等时,可以构建标准的效率矩阵,借助于独立零元素定理,对矩阵做有限步数的初等变化即可求出问题的精确解。近年来,随着对匈牙利算法和WTA问题的深入研究,武器与目标已经不局限于一对一形式,这意味着本文提出的混合算法在改进匈牙利算法之后能够解决更一般情形下的MS-WTA问题。

本文选择匈牙利算法作为初始解的生成策略,当所有阶段的待打击目标集合生成后,从武器库中选择一定数量的武器,计算统一效率矩阵,调用匈牙利算法计算当前打击次序下的局部最优解,然后作为初始解传入模拟退火算法。

2.2.2 模拟退火算法

模拟退火算法的设计借鉴了蒙特卡罗抽样思想和自然界中固体“退火”现象,常被用作求解组合优化问题,在解空间中寻找近似全局最优解[33]。在MS-WTA研究中,目标函数可以认为是固体的内能,在高温情况下算法在内部迭代中可以以较高概率接受差解,随着温度下降、算法逐渐趋于稳态,直至到达停止准则,找到问题的近似最优解。本文使用该算法求解MS-WTA问题的流程如算法2所示。

算法 2 模拟退火算法输入: 初始解s0,初始目标函数值f0输出: 全局最优解和最优目标函数值sg,fg1 参数初始化:T0、Tk、Tf、Δd、ψ2 while T>Tk do3 for i in range (1,ψ) do4 调用阶段调整算子获取新解stemp5 if failflag=0 then6 基于HA计算局部最优解Snew,fnew7 if Metrospoli’s mark=1 then8 更新松弛系数值RC9 S0←snew; f0←fnew10 end if11 end if12 end for13 if f0

在模拟退火的框架下,通过随机方式选择相邻两个阶段,通过实现阶段间机动性强的目标的波次改变来调整各阶段打击顺序。本文设计了两交换(点式)阶段调整算子和段式调整算子。其中,点式阶段调整算子用于小规模WTA的最优解搜索,而段式调整算子通过批量式交换打击阶段,实现原打击序列的大范围调整。本文使用的阶段调整算子的流程如算法3所示。

算法 3 目标的阶段调整算法输入: 初始目标打击序列F输出: 新的目标打击序列F', 阶段调整成功参数failflag参数初始化:recycleflag,counter=0,failflag=0根据所求解问题的规模选择阶段调整算子,随机地选择相邻的阶段(Nt,Nt+1)While recycleflag=1 do在Nt中随机选择可交换的目标g1基于RC调整准则判断可行性if RC(g1)=1 dorecycleflag=0elif counter 超出武器超出目标数量dofailflag=0breakend whileif failflag=0 do在Nt+1中随机选择相等数量的目标g2产生并输出新序列F',否则输出F

(1) 两交换阶段调整算子

将WTA分成s个阶段,算法将从s-1对相邻阶段中选取阶段调整的对象。该过程如图2所示,从第t阶段的可松弛目标集合中随机选取交换的对象,同时从第t+1阶段任意选择目标,两两交换完成阶段的调整。该算子适用于小规模WTA,通过小的扰动搜索出高质量目标阶段分配。

图2 两交换阶段调整算子

(2) 段式阶段调整算子

段式阶段调整算子同样以随机方式选取相邻阶段的目标集合,但是两阶段目标的交换不再是“点对点”的小规模改变。如图3所示,首先在第t阶段的目标序列中选取一个固定长度的目标片段,同时在第t+1个阶段中选取任意一个等长目标序列,交换打击的阶段,最后根据RC调整准则检查不合法的目标对,不改变原先的打击次序。大范围调整目标的打击次序的方式适合大规模WTA,能够剧烈地改变原先目标的攻击波次。对t和t+1阶段的目标集合来说,目标的数量不发生改变,避免了不对等交换造成各阶段待打击目标数量差异过大的问题,缓和了单波次武器发射的压力。

图3 段式阶段调整算子

3 实验分析

为了验证模型和算法的有效性,在配置Intel(R) Core(TM) i5-10210U CPU @ 1.60 GHz 2.11 GHz的计算机上,使用PyCharm编译器在python3.8.5的环境下开展实验分析。

实验采用10个随机生成的测试算例来验证算法的性能,并与变邻域搜索(variable neighborhood search, VNS)方法进行了对比实验,该算例中的数据使用了随机案例生成器产生,算例的规模和算法涉及的基本参数如表2和表3所示。表4展示了HSA算法和VNS算法在同样的环境下运行20次得出的平均目标函数值和平均运行时间,其中“-”表示VNS求解该问题耗时过长,不可接受。

表2 算例规模

表3 算法参数

表4 算法运行时间对比

为了验证本文算法的求解效果,统计了两种算法在外层循环框架下搜索到的解的分布,采用图4和图5所示的箱线图展示算法的求解效果。为了方便展示,选取了前4个算例的实验结果,其中图5是算例4更详细的展示。由实验结果可知,HSA算法在求解质量方面高于VNS算法,并且目标函数值分布集中,这是使用精确算法求解的优势所在。如图5所示,该场景包含4个阶段,15种武器类型以及60个目标(算例4),算法每次搜索出的局部最优解分布在355～360,对比VNS算法,解分布范围更大并且质量较差。在8个场景下,算法运行得到的目标函数值均优于VNS算法,并且实验表明,在目标数量相同的情况下,多波次筹划打击可以在更短的时间内取得更好的作战效果,如表4中算例5和算例6的对比结果。尽管算例6使用了较少的武器种类,但是通过增加打击阶段可以把运行时间缩短39%,目标函数下降2%。在10个算例的运行时间上,本文算法均明显优于VNS,说明本文提出以匈牙利算法替代局部搜索来寻找局部最优解的方式有着良好的计算性能。

图4 所提算法和VNS算法解的质量对比

图5 算例4的解的分布情况

4 结束语

针对战场远程精确打击过程中武器发射平台数量有限的问题,提出一种MS-WTA模型,依据重要性和目标打击的时间窗等因素给目标排列打击顺序、标记松弛符号,为目标的阶段划分提供了一种灵活的调整策略。在求解算法方面,设计了一种匈牙利-模拟退火结合的混合智能搜索算法,通过匈牙利算法计算每个阶段间武器和目标的精确匹配方案,减少了传统模拟退火方法以局部搜索寻找局部最优解的搜索时间。再借助于模拟退火框架对各阶段的可松弛目标进行调整,直到得出多阶段全局最优解。实验结果表明,在启发式方法中嵌入精确搜索方法对于提高解的质量和缩短求解时间有着显著优势,通过与HSA算法和VNS算法的对比实验进一步验证了HSA算法的有效性。

在下一步的研究中,将建立更加普适情形下的WTA模型,并针对常规导弹作战中的一对多、多对一和多对多等典型打击场景,研究数据和知识协同驱动的智能优化算法,探索大规模MS-WTA问题的高效求解算法。