汽车雷达多域联合调制波形

连红飞, 龙佳敏, 胡雪瑶,4, 蒋彦雯, 李东升, 范红旗,*

(1. 国防科技大学ATR全国重点实验室, 湖南 长沙 410073; 2. 北京理工大学信息与电子学院雷达技术研究所, 北京 100081; 3. 北京理工大学信息与电子学院CEMEE国家重点实验室电磁感知研究中心, 北京 100081; 4. 北京理工大学重庆创新中心, 重庆 401120)

0 引 言

毫米波雷达具有全天时、全天候的目标探测能力,且成本越来越低,逐渐成为智能驾驶系统中不可替代的核心传感器之一[1-4]。在汽车毫米波雷达中,常用线性调频连续波序列实现同时测距测速[5-8],但受射频前端和模数转换采样率的限制,雷达不模糊测速范围往往不能满足车载雷达探测需求,导致高速目标出现多普勒模糊的问题[9]。时分复用多输入多输出(time-division multiplexing multiple-input multiple-output,TDM-MIMO)波形由于工程实现简单且易于实现大的虚拟孔径进而提高角度分辨率,因此广泛应用在汽车雷达中[10-12]。但是TDM-MIMO波形由于各个天线分时发射,不仅导致时间、空间利用率低,而且降低了脉冲重复频率,加重了多普勒模糊的问题[13-15]。

针对上述应用问题,目前第一种解决思路是在TDM-MIMO波形基础上添加多重频波形,构造双波形探测的模式,其中,TDM-MIMO波形用于产生大的虚拟孔径以提高角度分辨率,而多重频波形则基于中国余数定理解决多普勒模糊问题。文献[16]最早将多重频解模糊方法应用到汽车雷达中,通过发射两个不同脉冲重复频率的调频序列波形,在提取出两个序列对应的模糊多普勒模糊频率后,再根据中国余数定理解多普勒模糊。但该方法存在以下缺点:首先,如果两个序列下模糊多普勒频率的测量不精确,就会导致最终解到的真实多普勒频率出现较大误差。其次,该方法构造了多个调频序列,就会导致发射时间增加,雷达探测周期增大,数据刷新率变慢,这对于汽车雷达实时处理是极为不利的[17]。第二种思路是在跟踪级解决多普勒模糊问题。该方法通过航迹关联,将目标与可能出现的多个模糊速度依次进行关联,通过滤波最终确定目标速度大小,其核心思想是距离微分法解模糊[18]。由于该方法需要对一个目标进行多假设关联滤波处理,因此运算量极大,影响雷达的探测性能[19]。最后一种解决思路是通过设计新波形,结合信号处理解决多普勒模糊的问题。文献[20-21]提出了一种交错频移调频序列波形,并利用序列之间的相位差解决汽车雷达多普勒模糊问题。但是该文献没有考虑二维快速傅里叶变换(fast Fourier transform, FFT)之后相位提取时的相位模糊问题,因此并不具备可实现性。文献[17]基于相位差解模糊的思路提出了一种交错变间隔调频序列波形,并分析了相位差解速度模糊的原理及过程。但是此波形并没有考虑在实际情况下雷达拥有多个发射天线时的情况,因此其不能兼顾多通道测角处理,在工程应用上有一定的局限性。

本文基于多发多收汽车雷达应用系统提出一种时、空、频多域联合调制波形,时域上进行脉冲重复间隔参差抖动实现序列分集,利用奇偶序列之间的抖动相位差完成速度解模糊,空域上进行多个发射天线的规律捷变实现目标匹配,频域上通过脉间相位调制实现多普勒频率正交,进而适配多通道测角处理。该波形可以有效解决了汽车雷达速度模糊问题,同时可兼顾多通道测角。与传统TDM-MIMO波形相比,本文提出的多域联合调制波形无模糊测速范围更大,时间空间利用率及相参积累增益更高。

本文的结构安排如下:第1节在介绍雷达片上系统和汽车雷达调频连续波序列信号模型的基础上给出波形设计的需求描述。第2节提出一种多域联合调制新波形,在介绍该波形及其信号处理方法的基础上给出其系统实现。第3节基于仿真及实际系统试验对比了新波形与传统TDM-MIMO波形的性能。第4节是结论。

1 调频连续波雷达原理

1.1 汽车雷达芯片介绍

本文基于TI AWR18xx片上雷达系统开展波形设计研究。首先对该系统做简单介绍。

TI AWR18xx片上雷达系统具有3个发射天线(TX1～TX3)和4个接收天线(RX1～RX4),射频模块功能框图如图1所示[22]。其中,Δφ为发射信号调制相位,ADC为模数转换器。

图1 TI AWR18xx雷达芯片射频部分功能框图

从图1中可以看出,斜坡发生器产生的调频连续波信号首先经过4倍频,然后经移相和功率放大操作之后由发射天线辐射出去,同时此信号也作为本振信号与接收到的回波信号进行混频处理。由于该系统多个收发通道共用同一个压控振荡器,因此不能同时进行频率调制,本文考虑通过脉间相位调制的方法实现多普勒频率正交。

本文所用的3发4收雷达阵列示意图及所形成的等效虚拟接收阵列如图2所示。nr为虚拟阵元总数,4个接收天线之间的间距为d,且d=λ/2,3个发射天线之间的间距为4d,即2λ。

图2 雷达阵列与等效虚拟阵列示意图

1.2 信号模型

汽车雷达常用的线性调频连续波序列如图3所示[23-26],其中fsw为扫频带宽。

图3 线性调频连续波序列

接收信号经过与发射信号混频后,经过低通滤波放大,对其进行采样,可得到第k个脉冲的中频信号形式[27-30]为

(1)

式中:f0为载频;Tr为脉冲宽度;R0为目标距离;c为光速;fB为中频频率;fD为目标多普勒频率。

(2)

(3)

式中:λ为波长。接下来,对上述中频信号进行二维FFT处理后便可得到频谱S(ri,vi):

(4)

式中:NZ、KZ分别为一维FFT与二维FFT点数。由以上结果可知,差频信号经过二维FFT处理之后,就可以估计出差频fB与多普勒频率fD,进而由式(2)和式(3)得到目标的距离与速度。

由图2中MIMO阵列模型可知,由目标角度θ带来的nr个等效虚拟接收阵元之间的相位差矢量:

因此在对通道数据进行提取之后,通过接收端数字波束形成(digital beam forming, DBF)即可得到目标的角度θ。

1.3 波形设计需求

在传统线性调频连续波序列中,最大不模糊多普勒频率等于系统重频,即fD,max=fr,对应的最大不模糊速度vmax=2fD,max/λ,即目标速度如果超过vmax就会产生模糊现象。目标多普勒频率与模糊多普勒频率的关系为

fD=fD,amb+q·fD,max,q∈Z

(5)

式中:fD,amb为模糊多普勒频率;q为多普勒模糊数。因此,多普勒不模糊波形设计的关键是将q限定为0或者通过信号处理解算可唯一求解的多普勒模糊数q。

下面结合汽车雷达实际应用场景和典型TDM-MIMO信号参数分析速度解模糊的必要性。假设雷达采用传统TDM-MIMO波形,距离分辨率为1 m,脉冲重复周期为50 μs,一帧内发射脉冲个数为64×3。则可以计算出雷达带宽为150 MHz,速度分辨率为0.2 m/s,无模糊测速范围为±6.5 m/s。设计参数如表1所示。

表1 汽车雷达系统典型参数示例

在实际道路场景下,雷达探测示意图如图4所示。

图4 雷达探测示意图

图4(a)中,自车与目标车辆同向行驶,考虑极端情况,假设自车速度为10 km/h,目标车辆行驶时速为160 km/h;图4(b)中,两车相向行驶,自车速度与目标车速度均为正常行驶速度80 km/h。因此,从上述两种情况分析,雷达不模糊测速最少要达到160 km/h,即44.4 m/s才可以满足车载雷达探测需求。而由表1参数可知,传统的TDM-MIMO波形下,±6.5 m/s的雷达无模糊测速范围远远达不到应用需求,因此研究具有多普勒解模糊且兼顾发射效率和角度测量能力的波形对汽车雷达至关重要。

2 多域联合调制波形

2.1 多域联合调制波形描述

本文基于TI AWR18xx雷达芯片,在传统线性调频序列的基础上,提出一种多域联合调制波形,发射信号时频关系如图5所示。该波形在时域上通过脉冲重复间隔参差抖动,实现序列交错分集,频域和空域上对多个发射天线进行脉间相位调制实现多普勒频率正交。

图5 多域联合调制波形时频图

时域上,该波形可分解为长度为K的奇、偶脉冲序列,其中奇脉冲序列中的脉冲时间间隔为T1,偶脉冲序列的脉冲时间间隔为T2,且T1=T2+a。该波形中所有脉冲的调频时长均为T2且调频带宽保持一致。频域上,3个发射天线之间通过脉间相位调制实现等间隔多普勒频分复用。其中,发射天线1不进行调制,发射天线2与发射天线1的多普勒频差为Δf1,发射天线3与发射天线1的多普勒频差为Δf2,且Δf1=Δf2-Δf1=fr/3。空域上,3个发射天线在奇偶序列中按照一定规律调制。在奇序列中,天线1与天线2同时工作,在偶序列中,天线1与天线3同时工作。

在多域联合调制波形中,多个发射天线间的多普勒频分复用是通过脉间相位调制实现,奇、偶两个序列中第m个(1≤m≤M)个发射天线的第k(1≤k≤K)个脉冲的调制相位量可表示为

(6)

2.2 多域联合调制波形信号处理

由于该波形中两个子脉冲的脉冲重复间隔不同,因此需要对奇、偶两个调频序列分别进行处理,两个脉冲序列等效的重复周期均为Tr。多域联合调制波形的回波信号处理流程如图6所示。

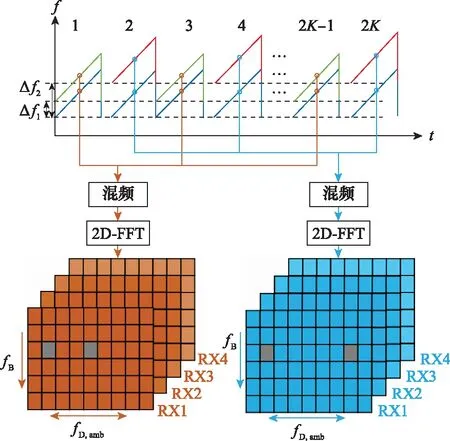
图6 多域联合调制波形信号处理示意图

奇序列与偶序列回波信号由4个接收通道数据组成,其经过混频、采样处理之后,奇偶序列中单个接收通道的中频信号可分别表示为

(7)

(8)

式中:φ1k、φ2k、φ3k分别为发射天线1～发射天线3的第k个脉冲的调制相位,由式(6)可知:

首先进行测距测速处理,由式(4)可知,对奇序列和偶序列的单个接收通道分别进行二维FFT处理之后,得到二维频谱Q1和Q2。对于单目标情况,两个序列经过二维FFT处理之后,频谱上分别出现两个目标点,其中一个目标点位置相同,另一个目标点虽位于同一距离单元内,但多普勒频率分别相差Δf1=fr/3和Δf2=2fr/3。由式(6)可知,奇序列与偶序列中,发射天线1的各个脉冲调制相位均为0。因此,两个频谱上相同点的位置即发射天线1对应回波信号的目标位置。由此位置的索引点即可得到目标的差频fB(对应距离)与模糊多普勒频率fD,amb,进而由式(2)和式(3)得到目标的距离与模糊速度。

在得到两个调频序列频谱上的目标位置之后,就可以按照文献[17]中相位差解模糊的思路,首先提取两个序列中峰值点的相位,并考虑相位卷绕,分别可以表示为

(9)

(10)

式中:φe为由于FFT栅栏效应导致的相位偏移;[·]表示四舍五入取整。

定义φd如下:

φd=ξ2-ξ1-2πfD,amb(T2+a)

(11)

将式(9)与式(10)代入可得

(12)

式(12)中,最后两项均为整数,令

(13)

由式(13)可知,-1/2≤δd≤1/2,如果要得到δd的值,就必须限制|qmax|a/(2Tr)≤1/4。其中,qmax表示目标可能出现的最大速度对应的多普勒模糊数。

因此,脉冲重复周期Tr与子脉冲的时间间隔差a以及最大速度模糊数的关系为

(14)

由于|qmax|a/(2Tr)≤1/4,δd可进一步表示为

(15)

则多普勒模糊数q为

(16)

式中:b的取值由δd的范围决定。当-1/4<δd<1/4时,b=0;当1/4<δd<1/2时,b=1/2;当-1/2<δd<-1/4时,b=-1/2。

在得到多普勒模糊数q之后,结合得到的模糊多普勒频率fD,amb,由式(5)就可以得到真实多普勒频率fD,进而求解出目标不模糊速度v=fDλ/2,至此便完成了速度解模糊处理。

由上述解模糊过程可知,Tr/a越大,可测的速度不模糊范围越大。但是值得注意的是,由于运算中存在取整的操作,因此相位测量误差的大小会影响多普勒解模糊的正确性,进而约束Tr和a等参数的选择,下面对其进行分析。

令

(17)

由式(16)可知,q=round(E)。因此,只有E的误差满足ΔE∈(-1/2,1/2)时,多普勒模糊数q才可被正确求解。

接下来逐项分析误差的影响。首先要使式(17)中第2项、第3项不解错,φd的求解误差Δφd需满足

(18)

因此,假设Δφd满足式(18),则只需考虑第1项。由E的误差传递式,可得

(19)

若要满足ΔE∈(-0.5,0.5)的条件,则相位测量误差[17]需满足

(20)

由式(20)可知,Tr/a越大,正确解模糊对于相位测量误差的要求就越高。在复杂道路场景下,若多个目标混叠导致相位测量误差超出此范围,就可能导致速度解模糊发生错误。

通过以上分析可知,最大多普勒模糊数与Tr/a正比,正确解模糊要求的相位测量误差范围与Tr/a成反比。因此,在进行雷达波形参数设置时候,需要综合考虑波形参数对于雷达解模糊性能的影响。

在完成距离、速度估计之后,最后利用多普勒频分复用形成虚拟收发阵列进行多通道测角。首先对目标点对应的多通道数据进行提取,分离回波信号。这里提取奇序列中发射天线1、发射天线2分别应的4个接收通道数据和偶序列中发射天线3对应的四个接收通道数据。由上述分析可知,偶序列目标点相位与奇序列相差2πfD(T2+a),因此在获得发射天线3的4个接收通道数据之后,首先应补偿此相位,再按照发射天线次序依次排列形成12个虚拟收发通道,最后利用数字波束形成算法完成测角处理。

综上,多域联合调制波形的数据处理流程如图7所示。

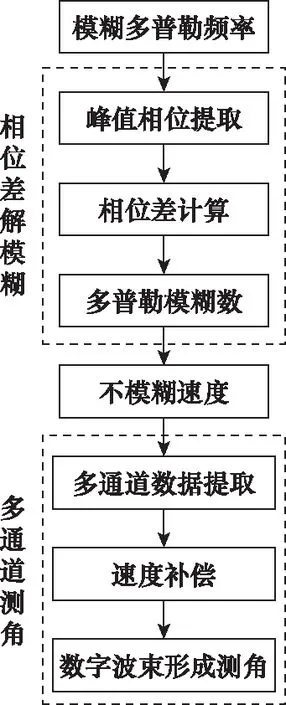
图7 多域联合调制波形数据处理流程

2.3 多域联合调制波形实现

本节简要介绍基于德州仪器(TI) AWR18xx芯片的多域联合调制波形实现方案。

TI AWR18xx雷达芯片支持通过定义chirp profile以及通过配置chirp RAM在这些profile上的变化来控制一帧内每一个chirp的参数。Chirp profile是基本的chirp参数设置模板,用于定义chirp的起始频率、调频斜率、脉冲宽度等参数。雷达芯片允许编程最多4种不同的profile。此外,最多512个独立的chirp可以预先编程并存储在配置RAM中。RAM中定义的每个chirp可以属于多个profile中的任意一个,并且可以在某些参数中,通过抖动与其profile配置文件不同。具体地,RAM中可以定义每个chirp中脉冲长度抖动值、起始频率抖动值等参数及控制多个发射天线使能。此外,TI还提供了每个chirp对应的发射天线移相器配置接口,用于改变每个chirp发射初相位。

本文基于TI AWR18xx雷达芯片,完成了多域联合调制波形的实现,实现过程如下。首先定义两个profile,profile1中脉冲宽度为T1,profile2中脉冲宽度为T2,其余参数如起始频率、调频斜率等均相同。然后在profile1下通过RAM对奇序列中的每个chirp进行配置,每个chirp中发射天线1与发射天线2使能。同理,在profile2下通过RAM对偶序列中的每个chirp进行配置,每个chirp中发射天线1与发射天线3使能。最后对每个chirp移相器接口进行配置,奇偶序列中每个chirp对应的发射天线的初始相位如式(6)所示。多域联合调制波形配置示意图如图8所示。

3 仿真分析与实验测试

本节从仿真与实测两方面验证多域联合调制波形的有效性及参数估计性能。

3.1 波形有效性仿真分析

本节仿真试验的波形参数如表1所示,设置子脉冲时间T1=60 μs,T2=40 μs,奇偶脉冲个数均为96个。由式(14)可以计算出最大可测多普勒模糊数|qmax|=5。为了验证多域联合调制波形在多目标场景下探测性能的有效性,仿真设置了距离、速度和角度各不相同的4个点目标。目标参数与估计结果如表2所示。对仿真回波数据进行二维FFT后得到的距离多普勒图如图9所示。经峰值点匹配后的4个目标见图9中标注。

表2 仿真目标参数估计结果

图9 多目标二维频谱

由表2中估计的结果可知,本文提出的波形可以准确实现目标参数估计,仿真验证了多域联合调制波形的有效性。

3.2 参数估计性能对比分析试验

该试验将多域调制波形与与汽车雷达常用的TDM-MIMO波形进行对比分析。

首先,在发射脉冲数和相参处理时间相同的情况下,分析两种波形的速度解模糊性能。由于在多域联合调制波形中,序列进行了分集,因此设置子脉冲时间T1=60 μs,T2=40 μs,而时分MIMO波形脉冲重复周期设置为50 μs,其余参数均与表1保持一致。根据第1.3节分析,假设雷达的速度探测范围为-45 m/s到45 m/s,则传统TDM-MIMO波形与多域联合调制波形速度估计结果分别如图10(a)和图10(b)所示。

图10 速度解模糊效果对比

由结果可以看出,在脉冲个数和相参积累时间相同时,多域联合调制波形可以获得更大的速度不模糊范围,相比于TDM-MIMO波形,无模糊测速范围提升近7倍。

其次,在脉冲个数K相同的情况下,多域联合调制波形的相参积累增益提升K/2倍,而时分MIMO波形提升K/3倍。因此,在脉冲数相同的情况下,多域联合调制波形相比于TDM-MIMO波形,相参积累增益可提升1.76 dB,对应的目标检测能力和测角精度均可获得相应的提升。

3.3 试验测试

本节通过设计的汽车雷达原理试验系统来测试多域联合调制波形的实现效果。试验系统由雷达模块、数据采集模块以及上位机模块组成,试验验证系统总体架构和实物分别如图11和图12所示。

图11 试验验证系统总体架构

图12 试验系统实物图

本节试验在外场空旷场景下进行,合作目标分别为向雷达靠近的速度较低的电动车与远离雷达速度较快的汽车。且据车载仪表盘显示,电动车速度为4.17 m/s,汽车速度约为12.5 m/s。试验中,规定远离雷达的方向为正速度方向,靠近雷达的方向为负速度方向。试验场景如图13所示。

图13 试验场景图

试验中出于安全性和合作目标控制的稳定性考虑,需要减小多普勒模糊测速范围。因此,改变T1为210 μs,T2为150 μs,其余参数如表1所示。通过实测参数计算可知,理论上最大可测速度对应的模糊数为6,因此不影响试验的验证目的。将采集下来的回波数据进行奇偶序列分集之后,分别对其进行二维FFT处理,得到其距离多普勒图如图14所示。

图14 实测数据进行二维FFT处理之后的距离多普勒图

按照图7中多域联合调制波形速度解模糊处理流程,得到的两个运动目标的速度估计结果如表3所示。

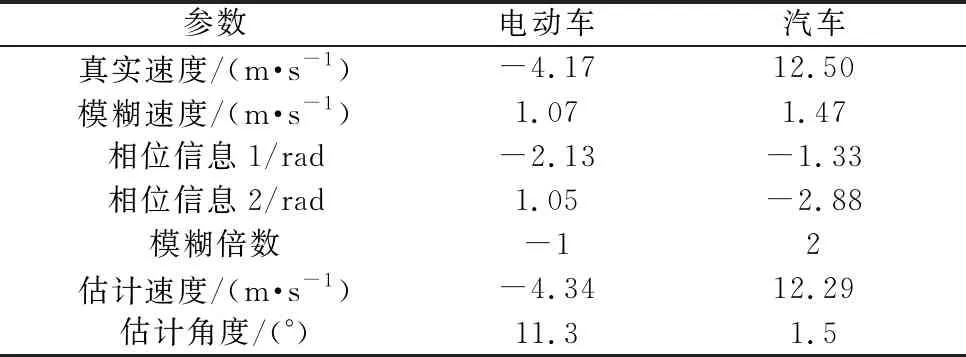
表3 试验目标参数估计结果

由估计结果可以看出,在本文提出的多域联合调制波形下,估计出的目标速度与真实速度基本相同,试验结果进一步验证了本文提出多域联合调制波形在实际系统中的可用性。

4 结 论

针对传统汽车雷达TDM-MIMO波形存在的时间、空间利用率低及高速目标多普勒模糊等问题,本文提出了一种时、空、频多域联合调制波形。该波形在时域上进行序列分集,利用脉冲重复间隔抖动带来的相位差进行速度解模糊,通过空域及频域上多发射天线的脉间调相实现多普勒频分复用。多目标仿真测试及外场实测结果表明,该波形在兼顾发射效率的同时具有优良的无模糊测速和多通道测角能力,对汽车雷达工程实践具有较强的应用价值。同时,本文所提多域联合调制波形设计及其信号处理方法也可扩展用于低成本导引或防撞探测系统。