基于混合本征模匹配的光刻掩膜分析方法研究

刘 佳, 苏 珉, 徐群玉

(1. 北京航空航天大学前沿科学技术创新研究院, 北京 100191; 2. 广西师范大学电子与信息工程学院,广西 桂林 541004;3. 中国民航科学技术研究院民航法规与标准化研究所, 北京 100028)

0 引 言

波导以及光波导器件的电磁特性分析仿真算法可扩展应用于计算光刻问题,为摩尔定律的进一步延续提供支持[1-3]。模式匹配是解决波导结构问题的常用方法[4-5],该方法早期采用纵向电磁场波动方程模型,目前主要采用横向电磁场波动方程进行模式匹配建模,较好地克服了传统波导分析方法中未知量过大的问题[6-7]。随着数值模式匹配以及计算性能的快速发展,基于有限元或者有限差分方法的数值模式匹配技术已经具备分析高复杂度波导结构的能力[8-10]。研究表明,模式匹配方法可应用于特定周期结构的电磁特征分析[11-12],在周期较大的情况下亦可用于非周期光刻掩膜结构的分析。

模式匹配方法的基本原理是采用本征模展开的形式对波导不连续处两端的横向电磁场进行匹配。因此,模式匹配方法的核心在于求解波导本征模及其展开系数。传统模式匹配通常采用复杂度为O(N3)的谱分解方法计算本征模[13],在求解电大尺寸高复杂度结构的本征模时计算效率瓶颈较为突出。为解决上述问题,研究人员提出了一种基于Lanczos方法的隐式模式匹配方法[14-15]。该方法通过重组横向电磁场波动方程,直接匹配波导不连续处的横向电磁场,并采用Lanczos算法求解波导结合处的横向电磁场。该方法不需要直接求解波导的本征模,且整体计算复杂度为O(N1.5)[16]。然而,该方法的效率优势是以计算精度的损耗作为代价的。作为隐式模式匹配的核心,Lanczos算法在迭代过程中没有采用严格正交策略,基向量的正交性随着迭代步数增加而逐渐缺失,影响了本征模的计算精度。此外,传统隐式模式匹配方法还存在分析多层结构时未知量过大,本征模传播特性不清晰等问题。这些问题使其并不直接适用于计算光刻问题。

本文以隐式模式匹配方法为基础,提出一种基于Krylov子空间理论[17]的混合本征模重构及显式模式匹配算法,在提升本征模精度的同时将计算复杂度控制在O(N1.5)。采用波导和周期结构对混合本征模的精度进行了验证。结合高频结构仿真器(high frequency structure simulator, HFSS) 软件以及严格耦合波分析(rigorous coupled wave analysis, RCWA)算法[18-20]的计算结果,对模式匹配算法的精度和效率进行了验证。通过对高复杂度光刻掩膜部件进行仿真分析,进一步证明算法在解决复杂计算光刻问题中的应用价值和效率优势。

1 隐式模式匹配及混合本征模重构

1.1 隐式模式匹配技术

基于有限差分数值建模方法,横向电磁场波动方程[21]可描述为

(1)

(2)

式中:符号～和^分别表示前向和后向差分计算。式(1)和式(2)可用紧凑型算子进行描述:

(3)

(4)

与常见迭代算法类似,初始矢量v0是任意定义的。新的基函数定义为

(5)

假设基函数之间满足正交性,可以推导出:

(6)

式(4)的迭代过程可转换为

Le·vj=βj-1vj-1+αjvj+βjvj+1

(7)

上述迭代过程可采用矩阵形式进行描述:

(8)

式中:βk[0,…,0,vk+1]表示误差项;矩阵Vk中的每一列对应一个基函数v。式(8)表明矩阵Le可采用一个低维空间Vk的线性展开进行描述,展开系数则为式中三对角矩阵中的元素。采用矩阵T描述上述三对角矩阵,则矩阵Le可以近似描述为

Le·V=V·T

(9)

矩阵T的维度为M,M与N的关系通常为M～cN0.5,其中c为常数。这是隐式模式匹配计算复杂度保持在O(N1.5)的根本原因[25]。矩阵V中的每一列向量对应Lanczos算法生成的基函数向量。基于泰勒展开公式,式(9)可进一步演化为

f(Le)·V=V·f(T)

(10)

式中:f(Le)表示矩阵Le的函数。若需要计算矩阵函数与向量的乘积f(Le)·v,则可以选取向量v作为Lanczos算法的初始向量迭代生成基函数矩阵V以及三对角矩阵T,将问题转化为

f(Le)·v=f(Le)·V·e1=V·f(T)·e1

(11)

式中:向量e1用于从矩阵中提取出第一列向量。矩阵T可采用谱分解算法进一步分解为

T=Q·Λ·Q-1

(12)

式中:矩阵Λ是本征值对角矩阵。矩阵Q的列向量对应Λ的本征向量。将式(12)代入式(11)可得:

f(Le)·v1=V·Q·f(Λ)·Q-1·e1

(13)

式(13)将复杂的算子矩阵函数转化为简单的对角矩阵函数,降低了计算复杂度。

1.2 混合本征模重构方法

定义矩阵Q中的第i列为基函数向量qi,V·qi可视作矩阵Le对应于特征值λi的本征模。然而,Lanczos算法在基函数的迭代生成过程中没有采用严格的正交策略,基函数之间的正交性随着迭代次数逐渐降低。因此,对需要高阶本征模的复杂结构,采用V·qi作为本征模近似是不合理的。

针对上述问题,本文采用Arnoldi[26-27]方法对Lanczos正交性缺失导致的模式匹配误差发散问题进行了修正。Arnoldi方法同样源自于Krylov子空间理论,但是在子空间描述及基向量生成过程中采用了不同的数值策略。在Arnoldi方法中,基函数生成采用如下迭代策略:

(14)

式中:采用符号u表示基函数,用于与Lanczos算法基函数v进行区分。与式(4)进行对比,Arnoldi和Lanczos算法的显著区别在于右手项的第2项。Arnoldi方法采用的是改进Gram-Schmidt正交策略,正交化过程中考虑了之前所有基函数。Lanczos算法仅考虑相邻两个基函数进行正交化,这种非严格的正交策略是Lanczos算法基函数正交性随着迭代步数增加而逐渐缺失的根本原因。Arnoldi算法的基函数同样根据式(5)进行定义,式(6)中的属性也适用。根据式(14),定义系数:

(15)

根据基函数之间的严格正交性,可得:

(16)

由于系数hij的特殊性,展开矩阵不是Lanczos算法的三对角矩阵,而是上Hessnberg矩阵的形式[28]。该展开关系可用下式进行描述:

(17)

混合本征模重构方法利用矩阵U中基函数的严格正交特性,保留了Lanczos的三对角矩阵T作为Le的特征值近似描述,采用投影矩阵U替代V,将U·qi作为混合本征模。由于U和V都是Krylov子空间投影矩阵,因此混合本征模U·qi在物理概念上与Krylov子空间一致,而严格正交的投影矩阵U使得U·qi具备更好的正交性和数值精度。矩阵U的生成需要消耗更多的运算资源,但是在模式匹配过程中仅需计算一次,因而对计算过程的实际运算效率不会产生显著影响。

1.3 周期边界条件

传统模式匹配问题通常采用理想电导体(perfect electric conductor,PEC)边界条件,但是与计算光刻问题的实际物理条件不符。本文采用了周期边界条件(periodic boundary condition,PBC)[29-30]对计算光刻问题进行建模,如图1所示。横向电磁场的周期边界条件可描述为

图1 周期边界条件示意图

(18)

式中:参数a和b为X和Y方向上的周期长度;kx和ky分别表示X和Y方向上的波数;非斜体符号j则用于表示虚数。通过设定足够大的周期可将该边界条件扩展至非周期结构的建模。

2 光刻掩膜建模及显式模式匹配

光刻掩膜是光刻机的核心部件,其衍射及透射特性分析是计算光刻学中的重要问题。该部件可用波导结构结合周期边界条件进行建模。图2所示为无基座光刻掩膜的建模示意图,蓝色区域为光刻掩膜部件。附带基座的光刻掩膜部件可用多节波导结合周期边界条件进行建模。

图2 光刻掩膜部件波导建模示意图

本文以隐式模式匹配为基础,提出基于混合本征模的显式模式匹配方法求解结合处的横向电磁场。首先将Le和Lh采用互相关矩阵进行描述:

(19)

算子A和B的具体定义见文献[21]。图3所示为多节波导结构中的未知电磁场定义示意图。

根据图3,第一个结合点处的模式匹配为

(20)

矩阵Mm,n的定义为

各校食品质量与安全专业实习基本也存在上述问题。针对食品质量与安全专业学生在实习过程中发现的问题，我们在学校和学院层面采取了一些行之有效的措施。

(21)

式中:矩阵On,m为插值矩阵,保证结合处两端未知量的一致性。消除式(21)中的反射电场可以得到:

(22)

式(22)中的电场可用混合本征模展开:

(23)

(24)

波导的中间段可采用类似方法进行匹配:

(25)

采用混合本征模可将式(25)转化为显示模式匹配:

(26)

波导的最后结合处可通过匹配传输电场得到:

(27)

通过消除式(27)中的传输电场可将式(27)转换为

(28)

采用混合本征模进行展开后可得到:

(29)

将式(24)、式(26)以及式(29)进行重组可以构建块矩阵求解本征模展开系数。以四节波导结构为例,其对应的块矩阵为

(30)

式(30)中块矩阵第1行描述了第1个结合处模式匹配,子矩阵Ψ11对应式(24)的左手第1项。块矩阵第2至第5行对应中间段的波导模式匹配。块矩阵最后一行描述了最后一个结合处的模式匹配。式(30)中块矩阵的维度要明显小于隐式模式匹配的块矩阵,求解效率更高。算法的计算复杂度维持在O(N1.5)的水平。在存储复杂度方面,由于需要在计算过程中存储混合本征模进行模式匹配,因而存储复杂度要高于隐式模式匹配。

3 结果分析与讨论

本节首先采用经典波导结构验证混合本征模以及显式模式匹配方法的精度。在此基础上,以高复杂度光刻掩膜为仿真案例,将显式模式匹配算法与HFSS软件以及RCWA算法在精度和效率上进行比对,验证本文提出方法在高复杂度计算光刻问题上的实用价值。

3.1 混合本征模及模式匹配方法精度验证

本节选取矩形介质波导对混合本征模的精度进行验证。该波导结构在XOY平面上纵横比为2,中心介质区域相对介电常数为2.25,有限差分网格数量为10 000。本征模Ex11,Ex21,Ex12以及Ex22的电场强度分布如图4所示,虚线标注了波导的中心区域与包层的边界。图4中本征模分布特征与文献[6]中的解析本征模高度一致。根据文献[6]中定义,图4中本征模对应的归一化频率均为2.5,归一化的传播系数分别为0.83,0.74,0.46 和 0.37。图5(a)和图5(b)为矩形介质波导的色散曲线,纵横比分别为2和1.5,中心区域的相对介电常数为2.25,色散曲线数值与文献[6]中解析解的均方根误差分别为0.007与0.01,表明混合本征模具备较高精度。

图4 矩形介质波导本征模电场强度分布

图5 矩形波导色散曲线

采用图6所示的周期结构对显式模式匹配方法进行进一步验证,几何参数单位为μm。中心区域相对介电常数为10,厚度为0.3 μm。图7所示为TE和TM极化电磁波正入射情况下周期结构的反射和传输系数,其中TE极化定义为入射电场与图6中的横轴平行,TM极化定义为入射电场与纵轴平行。两种极化模式下的计算结果与HFSS软件以及RCWA算法的计算结果取得了较好的一致性。以HFSS计算结果为基准,可对比传统隐式模式匹配与显式模式匹配方法在相同迭代步数下的精度。表1所示为反射与传输系数的归一化均方根误差,可以看出迭代步数越多,计算精度越高。本文提出的显式模式匹配方法采用混合本征模修正了正交性缺陷,因此在相同迭代步数下,具备更高的计算精度。

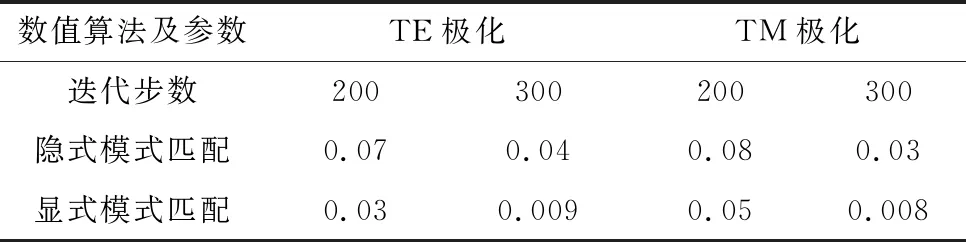
表1 隐式和显式模式匹配方法均方根误差比对

图7 矩形周期结构反射与传输系数

3.2 高复杂度光刻掩膜结构仿真示例

本节通过一个高复杂度光刻掩膜部件仿真案例,对显式模式匹配方法进行进一步验证。该部件的几何示意图如图8所示。光刻掩膜部件位于区域A,黑色区域相对介电常数为10。区域B为结构缓冲区并采用自由空间进行填充。该部件在XOY平面上呈二维周期分布特性,因此采用三节波导结构结合二维周期边界条件进行建模。区域A的长度宽度以及厚度分别为2 245 nm、708 nm以及50 nm,有限差分网格数量为215 000。激励源为TE极化模式下的正入射平面波。图9所示为光刻掩膜结构传输电场强度分布。图10(a)和图10(b)分别为采用HFSS、显式模式匹配、隐式模式匹配以及RCWA算法得到的传输系数以及横向传输电场的相位结果,3类方法的结果与HFSS体现出较高的一致性。为进一步描述结果相似度,采用归一化均方根误差对传输系数和相位的计算精度进行量化描述。传输系数的误差评估是在转换为线性单位后进行的,对应结果如表2所示。从表2中数值可以进一步看出3类方法的计算结果与HFSS结果是较为接近的。

表2 3类计算方法与HFSS计算结果的均方根误差比对

图8 高复杂度光刻掩膜部件几何结构示意图

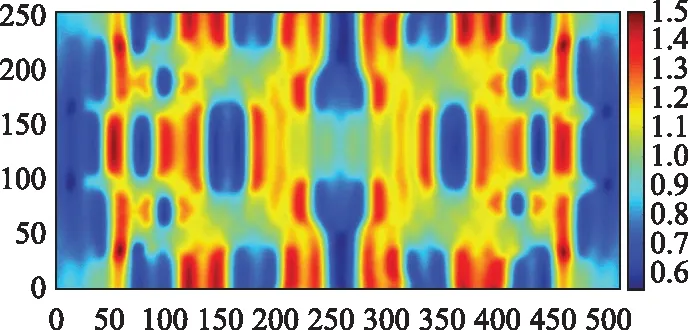
图9 光刻掩膜结构传输电场强度分布图

图10 4类计算方法的光刻掩膜仿真结果

3类方法的性能差异主要体现在计算效率层面。RCWA算法基于Floquet原理,适用于分析周期结构。该方法采用傅里叶变换将模式匹配投影到傅里叶域,数学描述简洁且对于简单结构具备解析解。然而,RCWA算法仍采用复杂度为O(N3)的谱分解方法计算本征模。表3对比了3类方法的平均计算时间。为保证效率比对的公正性,隐式和显式模式匹配的收敛迭代步数设定为3 700,RCWA算法在傅里叶域所需的本征模个数为3 721。RCWA算法计算时间最长,且大部分时间消耗在谱分解计算过程中。两类模式匹配方法计算时间基本上处于同一水平。显式模式匹配由于块矩阵维度更低,在计算效率上略高。此外,在混合本征模重构过程中,Arnoldi投影矩阵U仅需要计算一次并存储在内存中,无需重复生成投影矩阵,通过额外的存储消耗提升了计算效率。表4对比了3类方法的平均内存消耗,隐式模式匹配具备明显的存储复杂度优势。

表3 3类计算方法平均计算时间比对

表4 3类计算方法内存消耗比对

3.3 算法复杂度分析

4 结 论

本文以隐式模式匹配方法为基础,提出了一种基于Krylov子空间理论的混合本征模重构及显式模式匹配方法,修正了隐式模式匹配方法在解决计算光刻问题时存在的若干问题,结合周期边界条件实现了对光刻掩膜部件电磁特性的分析。通过与其他计算方法在精度和效率上的比对,得出以下结论:

(1) 混合本征模重构算法可以实现对复杂结构本征模的精确计算。

(2) 基于混合本征模的显式模式匹配解决了隐式模式匹配方法存在的若干问题,并保留了其O(N1.5)的计算复杂度优势。

(3) 显式模式匹配算法更适用于高复杂度光刻掩膜结构的分析,相较于RCWA算法在精度和效率上均具备优势。