基于APDL 的潜艇浮筏结构优化设计与分析
徐匡迪,游彩霞,何雪松
(1.430070 湖北省 武汉市 武汉科技大学 汽车交通工程学院;2.430000 湖北省 武汉市 中国舰船研究设计中心 船舶振动噪声重点实验室)
0 引言
潜艇作为一种水下军事装备,因其声频信号不容易被检测到而具有隐身性能。在所有需要提高的性能指标中最重要的就是隐身性能,这直接关乎作战成败,也是潜艇设计建造的出发点[1]。
为了增强潜艇的声隐身性,必须在振动噪声传递途径上采取隔振措施。浮筏隔振系统是潜艇上一种常用的隔振装置,主要由设备、浮筏结构、隔振器和基座4 部分组成。它将潜艇中的电机、风机等多个动力设备通过隔振器弹性安装在一个公共弹性筏架(浮筏结构)上,再将筏架通过隔振器安装在基座上。其工作原理是利用系统中隔振器的阻尼和浮筏结构的设计控制并衰减振动能量,达到减振降噪的目的[2-3]。通过系统设计,浮筏结构固有频率可避开设备的主干扰频率,使系统各部件的阻抗失配,抑制结构噪声传递,从而有效隔离船舶主辅机等机械设备的振动,实现船舶结构噪声的降低[4]。
浮筏结构(中间质量)是隔振系统振动传递控制的一个重要环节,众多学者围绕其优化展开研究。余永丰等[5]以大型隔振系统为研究对象,分析其筏架的上下层支承边界特性对前几阶模态振型和频率的影响;张华良等[6]以隔振传递率为评价指标,建立浮筏结构的超单元降价模型并研究其质量、刚度和阻尼对系统隔振性能的影响;苏常伟等[7]以某型号发电机组浮筏隔振装置及其船体基座为研究对象,研究筏架转动惯量、刚度以及基座阻抗对隔振性能的影响;杨德庆等[8]以筏架的选材为出发点,设计了一种负泊松比浮筏结构,发现其在某些频段的振级落差较常用筏架有所提高,同时具有质量轻的特点;康逢辉等[9]以一种复合材料筏架为研究对象,采用数值仿真方法研究了模量、阻尼以及各面板厚度等对隔振性能的影响,结果表明,提高模量、阻尼以及增大上面板厚度有利于提高减隔振效果,同时进行了试验验证。
目前相关研究的目标主要集中在浮筏结构的固有属性上,几何参数对固有频率影响方面的研究有所欠缺。本文设计了一种常用的平置板架式浮筏,使用ANSYS APDL 参数化语言对结构进行模态分析以及结构优化,在总体积一定的前提下,优化得到最合理的几何尺寸,使减振效果最佳,提高材料的利用率。同时,对单一参数绘制灵敏度曲线,进一步探讨其影响规律。
1 浮筏结构的建立
船用浮筏如图1 所示,浮筏结构与潜艇机组数量和放置位置相关。本文设计的浮筏为目前应用比较广泛的平置板架式结构,由上面板和下面板、5 块横向肋板、6 块纵向肋板以及带腰孔的侧板组成,顶部通过阻尼器支撑船舶上的设备(主要为发动机),底部通过阻尼器与船体相连,整个结构由钢材料制成。在软件中建立模型时,采用shell181单元模拟筏架,弹性模量210 GP,泊松比0.3,密度7 800 kg/m3。几何尺寸如表1 所示。

表1 浮筏结构几何尺寸Tab.1 Geometric dimensions of floating raft construction

图1 浮筏结构实物及有限元模型Fig.1 Physical object and finite element model of floating raft structure
Shell181 单元常用于厚度较薄的板壳单元,本文浮筏的板厚与其它参数相比很小,可以看作薄壳单元。在ANSYS 中定义壳单元厚度时有3 种生成方式:(1)从壳体中间向两侧生成厚度MID;(2)从壳体上表面生成厚度TOP;(3)从壳体下表面生成厚度BOTTOM。为研究不同生成方式对结果精度的影响,用3 种方式建模,获得其模态分析结果并绘制曲线,如图2 所示,可见精度有轻微影响但并不明显。本文采用MID 方式生成厚度。

图2 3 种单元厚度定义Fig.2 Three different cell thickness definitions
2 目标函数和设计变量的选取
在APDL 中,通过编写命令流将单一变量的变化数值存在数组中,在命令流中添加循坏语句,调用数组数据,建立参数化模型,进行自由模态分析。因为前6 阶为刚体运动,固有频率均为0,以筏架的总长度为研究参数,数值从1.2~1.5 m 取4 次,查看结构第7 阶~第16 阶固有频率的变化,如图3(a)所示。可以看出改变单一变量时每一阶固有频率的变动趋势一致,为便于后续研究,选择第7阶固有频率作为优化目标。
除了总长度,浮筏结构的几何参数还包括上、下面板厚度、总高、总宽、横纵向肋板厚度以及腰孔的长、宽尺寸等,但不是每个参数对固有频率的影响都那么显著。通过改变单一参数绘制固有频率灵敏度曲线,如图3(b)所示,其中各参数具体变动范围如表2 所示。从图3 可以看出,高度和上下面板厚度与固有频率成正比关系,其他参数成反比关系,并且长、宽、高对固有频率的影响较其它参数显著。

表2 参数变动范围Tab.2 Range of parameter variation
在实际工程应用中,为了保证能够支撑所有需减振的设备,一经设计后浮筏结构面板的长、宽不会变动,所以去除这2 个参数,将其余参数作为后续优化的设计变量。
3 优化设计
3.1 初始模态分析
优化设计就是对一个给定的模型,指定设计变量,在一定的约束条件下进行分析,通过不断修改设计变量重建模型对目标函数进行迭代计算。对结构优化设计而言,设计目标是优化的最终目的。设计目标通过目标函数体现,目标函数是设计变量的函数,通过目标函数可以对所有分析计算结果进行对比,找到设计目标的最优解。
ANSYS 优化模块使用3 个优化变量描述优化过程:(1)设计变量是自变量,用于与因变量构成函数来计算因变量,所有设计变量都有上下限;(2)状态变量是优化的约束条件,一般取应力、温度等,这里把体积作为状态变量;(3)目标函数是因变量,必须是设计变量的函数的最小值。改变设计变量的值就改变了目标函数的值[10~11],这里需要得到固有频率的最大值,所以在编写程序时将它的相反数作为目标函数。
运行1 次模态分析得到的第7 阶模态振型如图4 所示。此时固有频率为527.03 Hz,同时通过体积计算命令计算出模型的体积为0.092 4 m3。

图4 模态振型图Fig.4 Mode shape diagram
3.2 变量范围设置

表3 变量取值范围Tab.3 Range of variable values
优化过程中牵涉的数学模型:
APDL 在优化方法方面提供了多种算法,其中零阶优化算法比较常用[14]。零阶算法是在一定次数的抽样基础上,拟合设计变量、状态变量和目标函数的响应函数,从而寻求最优解,所以又称为子问题方法。其数学模型为
式(3)采用罚函数将其转化为无约束求最小值问题。
式中:xi——设计变量;gi、hi、wi——状态变量;X、G、H、W——罚函数。式(4)为X罚函数
式中:xu、xl——设计变量的上下限;c1~c4——常系数;ε——极小的正数。
3.3 优化结果
运行APDL,经过15 次迭代得到的结果如表4所示,第6 次迭代为本次浮筏结构的最优设计方案,优化结果如表5所示。各变量的收敛曲线如图5所示。

表4 迭代结果Tab.4 Iterating results
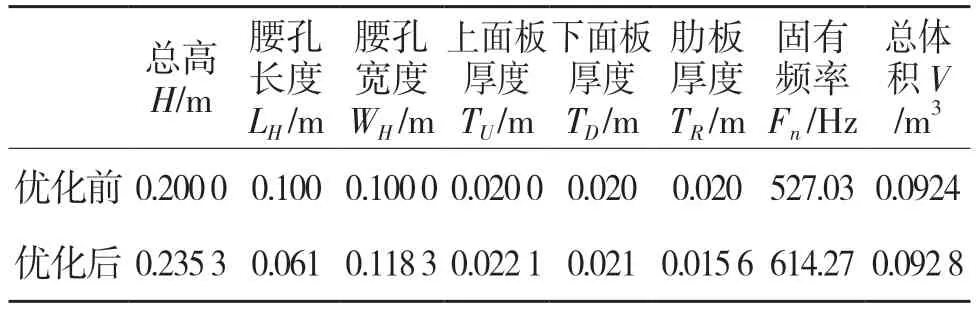
表5 优化结果Tab.5 Optimization Results

图5 优化变量收敛曲线Fig.5 Optimization variable convergence curve
第9 次迭代后目标函数取得了最小值-672.56,对应的固有频率达到了最大值672.56 Hz,但是总体积也增大到了0.1 m3,不符合设计要求。从经济性考虑,最后选择第6 次为本次优化的最优解,优化过后第7 阶固有频率增加了16.55%。为了使研究结果更具代表性,比对了优化前后7~12 阶固有频率,如图6 所示,可见不仅第7 阶,其他阶次的固有频率均有提升,达到了优化目的。

图6 优化前后结构的7~12 阶固有频率Fig.6 The 7~12 order natural frequencies of the structure before and after optimization
4 结语
本文提出改进浮筏结构尺寸优化减振效果,通过建立一个平置式浮筏结构的参数化模型,利用APDL design opt 模块对其进行优化。在总体积基本不变的前提下,迭代15 次并在第6 次取得了最优的设计结果,优化后目标提高了16.55%,得到了更加合理的几何尺寸,有效避开潜艇内机械设备主干扰频率,提高了结构的隔振效果。

