高压水泵主轴承压疲劳失效数值仿真

张孝元,王孝国,傅建平,马艳娥

(1. 晋中信息学院智能工程学院,山西 晋中 030800;2. 山西农业大学农业工程学院,山西 晋中 030800)

1 引言

高压水泵具有压力高、体积小与方便携带的优点,常常被用于清洗、喷雾与增压等方面。高压水泵主轴是一种通用的标准件,也是离心泵易损物件之一,同时,基于使用对象的需求,对水流速度与水压都有着较高的要求,泵体对设备稳定运行都有重要影响。如果主轴失效不仅会造成整个水泵出现故障,还会对其它物件造成损坏,带来较大的工作量和维修费用。因此,分析高压水泵主轴承压疲劳失效的形式,对水泵正常运行具有现实意义。

基于这个问题,有许多学者开展了相关问题的研究,其中,文献[1]中,陈兴江等人研究了主泵推力轴承失电惰转失效方法,该方法预先介绍了主泵轴承的结构特点和工作原理,并建立滑动轴承的特性曲线,对其失效情况进行了分析;文献[2]中,解江等人研究了典型螺栓连接CFRP薄壁C型柱轴压失效行为模拟方法,该方法建立失效形貌及载荷位移曲线,并建立柱层模型进行轴压仿真,完成对主轴失效行为的分析。上述文献提出的方法虽然能够对高压水泵主轴承压疲劳失效情况分析,但是实际的主轴疲劳失效情况是不断磨损产生的失效,中间涉及到的影响因素较多,导致现有的分析方法分析结果还存在一定的不足,为此对高压水泵主轴承压疲劳失效数值模拟优化方法,期望提高主轴承压疲劳失效分析的准确性。

2 主轴三维模型建立

以高压水泵主轴为研究对象,数值模拟之前建立水泵流场三维模型,建立过程如下所示:

第一,网格划分,为保证数值计算的成功,需要划分高质量的网格,在网格划分中需要保证生成的网络使物理求解域上的计算节点与求解域上的节点相互对应,不出现多重映射节点。基于上述分析采用分结构展开原则,定义叶轮网格,采用混合式网格类型划分高压水泵的网格;

第二,非结构网格光滑处理,网格光滑是非结构网络计算中不可缺少的环节,采用节点松弛法处理[3],将节点坐标移到与之相关联的节点组成的多边形的中心,将公式表示为

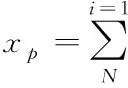
(1)

式中,xi代表第i个网格的数量。

第三,为保证节点松弛的顺利进行,采用网格关联质量约束条件,将公式表示为

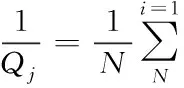
(2)

式中,Qi代表质量关联参数。

上述判断的主要目的是保证不出现负的体积元,并保证计算过程中将循环步数控制在三步以内。

第四,选择湍流模型[4],将湍流模型公式表示为

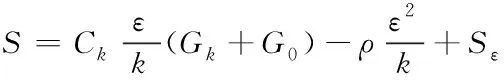
(3)

式中,Ck代表梯度湍动能产生项,k、ε分别代表经验常数,G0代表脉动扩张系数,ρ代表浮力端动能产生项,Sε代表耗散率。

第五,选择近壁区[5],将近壁区确定为标准壁面函数,将其表示为

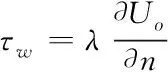
(4)

式中,∂n代表黏性长度,∂Uo代表Uo点的对称参数。

基于上述过程建立起高压水泵主轴的三维模型,为后续模拟提供基础。

3 损失参数计算

在上述三维模型建立的基础上,计算损失参数,即计算主轴承压疲劳数值的影响参数[6],将总功率损失参数表示为

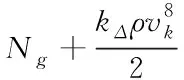
(5)

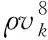
将流经叶轮前后运动状态与单位重量液体能量之间的基本方程[7]表示为

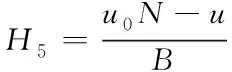
(6)

式中,u0代表初始转角速度,N代表液体能量参数,u代表能量变化参数,B代表理论修正参数。

汽蚀分目标函数计算[8],将叶轮汽蚀余量[9]计算公式表示为

(7)

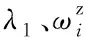
同时,在计算过程中,水泵主轴存在游隙,游隙的增大与减小都会对主轴承压能力产生影响。为此需要对这一问题解决,将主轴率表示为

Σρ=ρ11+ρ12+ρ111+ρ112

(8)

式中,ρ11、ρ12、ρ111、ρ112分别代表物体的主曲率。

在此基础上,采用应力计数算法进一步计算,应力计数算法主要对高压水泵主轴疲劳应力时间里程分析,对应力水平循环特征参数分离并计算[10]。假设高压水泵主轴零件某点的应力时间里程中任意四个点的应力值为X[n]、X[n+1]、X[n+2]、X[n+3],将两点之间的净应力值定义为

H[n]=|X[n+1]-X[n]|

H[n+1]=|X[n+2]-X[n+1]|

H[n+2]=|X[n+3]-X[n+2]|

(9)

当应力循环存在时,将净应力表示为

H[n]≥H[n+1],H[n+2]≥H[n+1]

(10)

式中,H[n]代表临界应力值。

在此基础上,计算偏离循环临界值[11]的程度

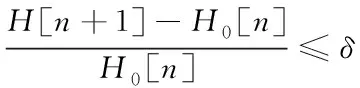
(11)

式中,δ代表预处理精度。

经过上述计算,计算损失参数,为后续分析提供基础。

4 载荷变形关系分析

轴承在安装、载荷适当的工作条件下时,会出现疲劳失效,为研究这个现象,根据轴承滚动体与滚道的基础情况构建接触模型。滚动体与滚道都属于非协调弹性接触的物理,当它们发生接触后,接触区域相较于总体来说是较小的,产生的接触应力也仅仅发生在接触区域的周围,为此在载荷变形分析上,研究轴承滚动体与滚道接触的部分区域,其接触示意图如图1所示。

图1 滚道接触示意图

在实际的接触问题求解上,作出以下假设:

1)接触区域为椭圆形;

2)将每个物体看作弹性半空间体;

3)忽略接触体的表面摩擦参数,考虑两个弹性体之间的传递参数和法向压力。

在上述假设条件建立的基础上,构建接触模型[12,13],将主轴承压区域扩展成为一个接触面,将公式表示为

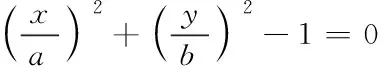
(12)

式中,a、b分别代表接触应力点,x、y分别代表x轴、y轴。

在此基础上利用表现受到垂直集中力作用的解,从垂直位移几何条件出发,分析轴承的负荷作用。在轴承滚子与滚道发生接触时,所产生的接触应力可以归于赫兹接触理论[14,15],为此根据赫兹接触理论,进一步对问题求解,将各个点的接触应力表示为

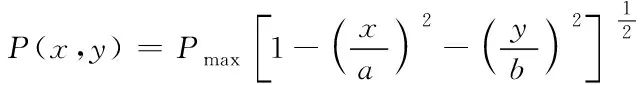
(13)

式中,Pmax代表接触的最大应力。

在此基础上将接触载荷与弹性趋近量表示为

Q=Kδn

(14)

式中,K代表两个接触体之间的载荷变形参数,δn代表第n次接触的法向趋近量。

通过上述过程分析了主轴承载时的接触情况,更好地体现出主轴承压能力的微观特性。

5 水泵主轴承压疲劳失效数值模拟实现

在上述准备工作完成的基础上,对水泵主轴承压疲劳失效数值模拟,整个过程如图2所示。

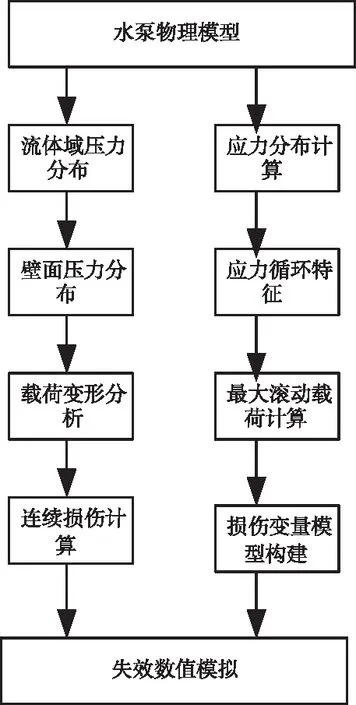
图2 主轴承压疲劳失效数值模拟流程

分析内部载荷分布情况,高压水泵主轴在工作过程中会同时承受径向载荷和轴向载荷,即在径向和轴向上均有位移情况。将滚道弹性变形量表示为

δψ=δasinα+(δcosψ-G/2)cosα

(15)

式中,α代表轴承接触角,G代表载荷方向的移动点。

根据受力平衡原理,各个滚动体在径向和轴向的受力之和应分别等于轴承所受的径向载荷和轴向载荷,将公式表示为

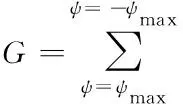
(16)

根据上述公式计算出最大滚动体载荷,获得主轴接触角的载荷分布。

将上述载荷分布参数作为标量,然后分析连续损伤力学问题,将方程表示为

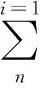
(17)

式中,Ni代表受到的损伤值,ni代表完全损伤临界参数。

损伤力学主要是以统计学为基础处理材料失效问题的,为此在此基础上定义材料点的损伤变量表示材料退化情况,将损伤本构方程表示为:

σij=Cijl(1-D)εkl

(18)

式中,Cijl代表材料弹性张量,εkl代表应变张量。

通过上述过程建立起损伤变量模型,经过计算能够完成水泵主轴承压疲劳失效数值的模拟。

6 实验对比

为验证所提出的高压水泵主轴承压疲劳失效数值模拟方法的有效性,进行仿真,并将主泵推力轴承失电惰转失效分析方法、典型螺栓连接CFRP薄壁C型柱轴压失效分析方法与所提出的方法对比,对比对象以及对比结果如下内容所示。

6.1 实验准备

此次研究采用某公司生产的高压水泵作为实验对象,该水泵的基本参数如下表所示:

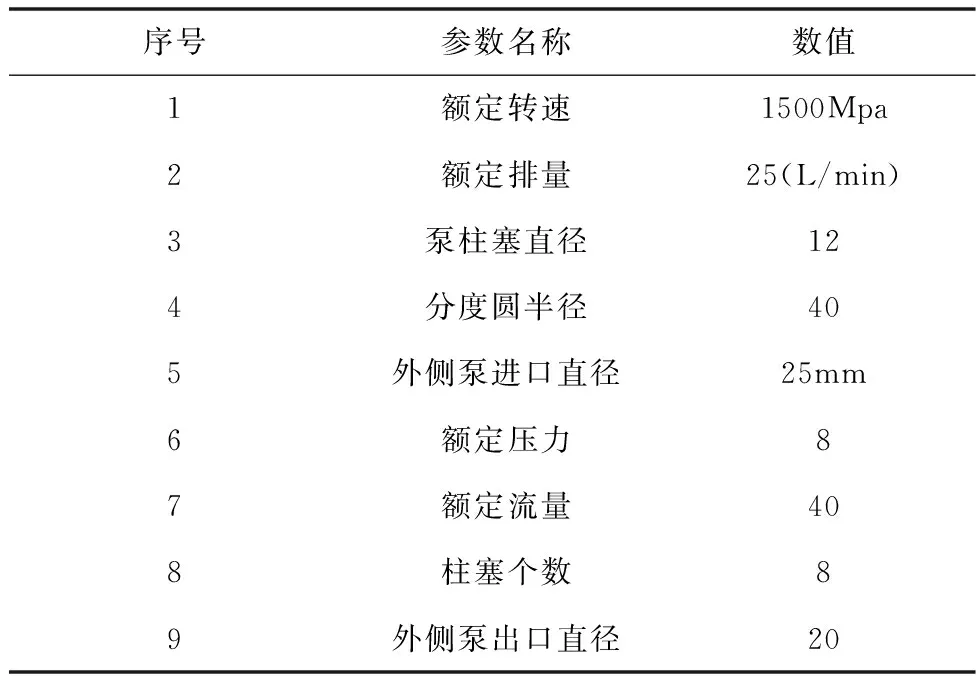
表1 实验水泵基本参数

在实验中运行高压水泵,仿真环境,分别对比不同形式下主轴失效数值模拟的效果。

6.2 泵腔静压模拟值对比

图3为三种方法模拟结果与实际的泵腔静压值的对比结果。

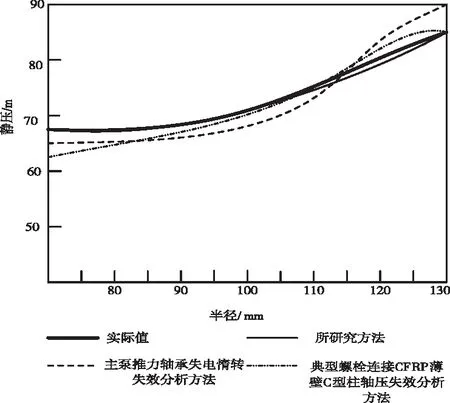
图3 泵腔静压模拟值对比

基于上图可知,在不同半径上,所提出的主轴承压疲劳失效数值模拟方法模拟结果与实际的值相差较小,较另外两种方法更接近真实值。原因是所提出的失效数值模拟方法能够有效分析各种阻力损失因素的影响,从而能够获得较为准确的模拟结果。

6.3 沿表面最大应力值变化情况对比

分别采用研究方法与另外两种方法模拟主轴表面最大应力值变化情况,如图4所示。

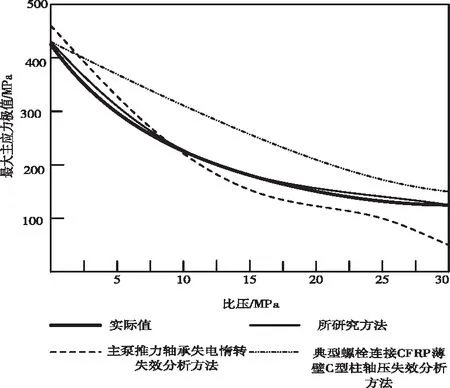
图4 沿表面最大应力值变化情况对比r.min-1

基于上图可知,所研究的模拟方法获得的最大应力值与实际的应力值基本保持一致,能够较为准确地模拟出主轴的最大应力情况,较另外两种方法模拟效果好。

6.4 不同水膜厚度下轴承承载能力分析

分别模拟计算不同水膜厚度下的轴承承载能力,分析结果如图5所示。

图5 不同水膜厚度下轴承承载能力分析

基于上图可知,随着水膜厚度的增加,水泵主轴的承载能力显著下降,所研究的模拟方法能够准确计算出结果,与实际的变化情况基本一致。而另两种方法计算结果与实际的承载力有较大差距,计算结果不是很准确。

6.5 不同转速下轴承承载能力分析

在此实验中,将水膜厚度设置为0.1mm,水腔厚度设置为3.0mm,计算在此情况下的轴承承载能力,计算结果如图6所示。

图6 不同转速下轴承承载能力分析

基于上图可知,随着转速的增加,静压轴承承载能力下降,可以看出转速是影响轴承承载能力非常重要的因素。而所研究的模拟方法能够较为准确地分析出不同转速下的轴承承载能力,与实际值基本一致,较另外两种方法应用效果好。

7 结束语

综上所述,完成高压水泵主轴承压疲劳失效数值模拟方法的设计,实验结果表明,所提出的方法具有较高的模拟准确性,并得出以下结论:

1)对损失参数进行了计算,考虑了多种因素对主轴疲劳失效数值模拟时的影响因素,在很大程度上提高了数值模拟的准确性;

2)建立了载体接触模型,多方面分析了主轴接触应力的分布情况,并考虑到实际情况,分析了在多摩擦情况下主轴承压的物理特性;

3)从实验结果看,所提出的方法能够准确分析出多种条件下的主轴情况,并且通过实验发现,随着水膜厚度的增加,轴承承载能力逐渐减小,因此可以借助这一结论,设计时轴承间隙要减小,以提高轴承的承载能力;

4)随着轴承转速的增加,承载力也逐渐下降,两者关系呈线性关系。

此次研究虽然获得了一定的结果,但是影响高压水泵主轴疲劳失效数值模拟效果的因素较多,在后续研究中还需要做进一步研究,进一步提高模拟效果。