基于精英反向学习和对数螺旋的HHO算法
唐剑兰,蔡茂国,徐 翔
(深圳大学电子与信息工程学院,广东 深圳 518000)
1 引言
在计算机科学、工程设计、运筹学、能源、商业及其应用等众多领域都有亟需解决的优化问题,然而,在当今时代和科技的发展背景下,优化问题变得错综复杂,梯度下降法和牛顿法等传统的数学方法难以去解决这些繁杂问题[1]。元启发式算法因其原理简单、灵活性高、易于实现等优点,被广泛的应用于处理优化问题。常见的元启发式算法有:基于进化的遗传算法和差分进化算法、基于物理的重力搜索算法和模拟退火算法、基于人类的脑风暴优化和基于教学学习的优化算法、基于种群的灰狼优化算法和鲸鱼优化算法等。
哈里斯鹰优化(Harris Hawks Optimization,HHO)[2]是近些年来一种比较新颖的基于种群的元启发式算法,因其具有修改参数少,扩展性好,寻优能力强的特点,故现在已在图像去噪[3]、特征选择[4]、资源调度[5]、深度学习[6]、轨道优化[7]等多个领域得到应用。
然而,HHO算法也会存在和其它群优化算法一样的“通病”,如易陷入局部最优、求解精度低。国内外一些学者对其进行研究改进,Dhawale D等人[8]提出一种改进的混沌哈里斯鹰优化算法(CHHO),即将帐篷混沌策略与传统HHO相结合来增强HHO的局部搜索能力。Al-Betar等人[9]结合进化算法的适者生存原则,在探索阶段采用锦标赛、比例和线性排名三种策略对HHO进行改进,其中锦标赛哈里斯鹰优化算法(THHO)性能最佳。Hussain K等人[10]提出一种具有长期记忆的HHO算法(LMHHO),即将多个有希望的搜索区域记忆存档,群体可以根据多种过去的经验来决定下一步行动,使得算法在探索和开发之间保持平衡。胡等人[11]受粒子群优化算法的启发,将速度加入到HHO的探索阶段,再利用人工树算法的交叉算子改进HHO中渐进式快速俯冲的软围攻和渐进式快速俯冲的硬围攻,得到一种改进的哈里斯鹰优化算法(IHHO)。
上述研究在一定程度上提升了HHO的性能,同时表明对HHO性能进行改进和提高具有意义性和研究性,故本文提出一种基于精英反向学习和对数螺旋的哈里斯鹰优化算法(Elite Opposition-Based Learning and Logarithmic Spiral Harris Hawks Optimization,ELSHHO)。
2 哈里斯鹰优化算法
HHO算法是对哈里斯鹰寻找和捕捉猎物过程中的协作行为进行数学建模,主要包含探索阶段及开发阶段,各个阶段的流程如图1所示。

图1 HHO阶段图
2.1 探索阶段
哈里斯鹰随机栖息在某些位置,并根据两种策略探测猎物,策略选择由随机数q决定。当q<0.5时,哈里斯鹰会根据其它成员和猎物的位置进行栖息;当q≥0.5时,哈里斯鹰会随机栖息在鹰群活动范围内的大树上,具体模型为

(1)

(2)
其中,X(t+1)表示哈里斯鹰在下一次迭代过程中的位置,X(t)表示哈里斯鹰在本次迭代过程中的位置,Xb(t)表示猎物的位置(即拥有最优适应度的个体位置),Xr(t)表示当前种群中随机选择的哈里斯鹰的位置,XAvg(t)表示当前种群的平均位置,ω=r3(LB+r4(UB-LB)),r和q表示介于0到1之间的随机数,LB、UB分别是探索空间的上限和下限,N为种群的数量。
2.2 探索阶段过渡到开发阶段
HHO算法根据猎物的逃逸能量E来判断HHO处于全局探索阶段还是局部开发阶段,其数学公式如下
(3)
其中,E0被设置为-1~1之间的一个随机数,代表猎物能量的原始状态;t表示当前迭代次数;T则表示最大迭代次数。若|E|≥1时,哈里斯鹰将继续探索以确定猎物的位置;若|E|<1时,表示猎物位置已确定,执行开发阶段,哈里斯鹰开始逮捕猎物。
2.3 开发阶段
HHO根据E和猎物逃脱概率r制定了四种策略。当r<0.5时,表示成功逃脱,当r≥0.5时,表示逃脱失败。
2.3.1 软围攻
当r≥0.5且|E|≥0.5时,表示猎物此时能量充沛,试图摆脱哈里斯鹰的追捕,但最终未逃脱成功,哈里斯鹰发动突袭并进行软围攻,猎物被软包围,位置更新公式如下
X(t+1)=ΔX(t)-E|J×Xb(t)-X(t)|
(4)
J=2(1-r5)
(5)
ΔX(t)=Xb(t)-X(t)
(6)
其中,J是介于0~2之间的一个随机数,表示猎物在逃跑过程中的跳跃强度。
2.3.2 硬围攻
当r≥0.5且|E|<0.5时,猎物逃跑能量消耗殆尽,哈里斯鹰将在发起最后突袭时进行猛烈围攻,猎物被直接捕获,位置由以下公式更新
X(t+1)=Xb(t)-E|ΔX(t)|
(7)
2.3.3 渐进式快速俯冲的软围攻
当r<0.5且|E|≥0.5时,猎物能量充沛并且成功逃脱哈里斯鹰的追捕,因此哈里斯鹰采用渐进式快速软包围圈来进行包围,其数学描述如下:
Y=Xb(t)-E|J×Xb(t)-X(t)|
(8)
Y=Y+S×LF(D)
(9)
其中,D表示当前问题维度,S是大小为1×D的随机向量,LF为莱维飞行函数,如等式(10)所示。

(10)
其中,μ和ν为0~1之间的随机数,β=1.5,该位置由以下公式更新
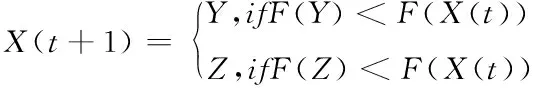
(11)
2.3.4 渐进式快速俯冲的硬围攻
当r<0.5且|E|<0.5时,模拟猎物逃逸能量不足但却成功逃脱的情况,此时哈里斯鹰快速发起突袭并进行猛烈硬包围,其数学模型为

(12)
Y′=Xb(t)-E|J×Xb(t)-XAvg(t)|
(13)
Z′=Y′+S×LF(D)
(14)
3 基于精英反向学习和对数螺旋的HHO算法
3.1 精英反向学习
算法的收敛速度和求解精度会受种群质量优劣的影响,若种群的值不在所求空间而在它相反空间,则会加大算法的寻优难度,甚至找不到最优解,因而种群的初始化和位置更新是种群优化算法中的重要一环。目前有许多学者采用反向学习和精英反向学习的方法来对其进行改进,如文献[12-14]。
反向学习(Opposition-Based Learning,OBL)是Tizhoosh[15]提出的一种机器智能策略,将其应用在初始化种群中可以有效提高解的质量。精英反向学习(Elite Opposition-Based Learning,EOBL)是在反向学习的基础上对其改进,它是通过种群中的精英个体来求解反向个体,再从候选方案内选取优秀个体(适应值更高的个体)来形成新的种群。
传统HHO算法初始化种群时是一个随机的过程,存在较大的偶然性和盲目性,因而会造成种群多样性低和收敛速度慢等缺点,为此本文采用精英反向学习策略来对其改进,具体步骤如下:
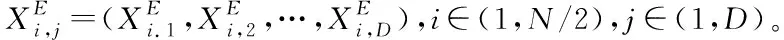

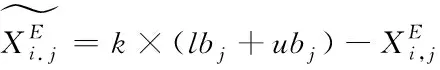
(15)
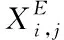
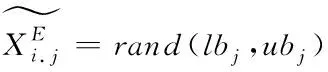
(16)
3)合并当前种群和精英反向种群,并对其适应值进行排序,选取前N个优秀个体作为新的种群。
本文在初始种群和每次种群迭代时都引入精英反向学习机制,通过该方法可以扩大种群的探索范围,使得算法在更广的范围内找到质量更优的解,提高种群的丰富性和算法的收敛速度。
3.2 对数螺旋
在元启发式领域,对数螺旋(Logarithmic Spiral,LS)这一概念被Mirjalili等人在2015年和2016年分别应用于飞蛾火焰优化算法(MFO)[16]和鲸鱼优化算法(WOA)[17]。MFO的灵感起源于飞蛾飞行这一行为,飞蛾实际上是通过与自然光源保持相对固定的角度来进行飞行,但由于人造光源会扰乱飞蛾的视线,通常观察到的飞蛾在光源附近是呈螺旋状飞行的,如图2[15]。WOA是一种模仿鲸鱼捕食行为的优化算法,它使用螺旋状来模拟座头鲸的泡沫网攻击机制,如图3[16]。将螺旋飞行运动的数学模型集成到MFO和WOA中可以有效的提高算法的空间搜索能力,具体公式如式(17)所示
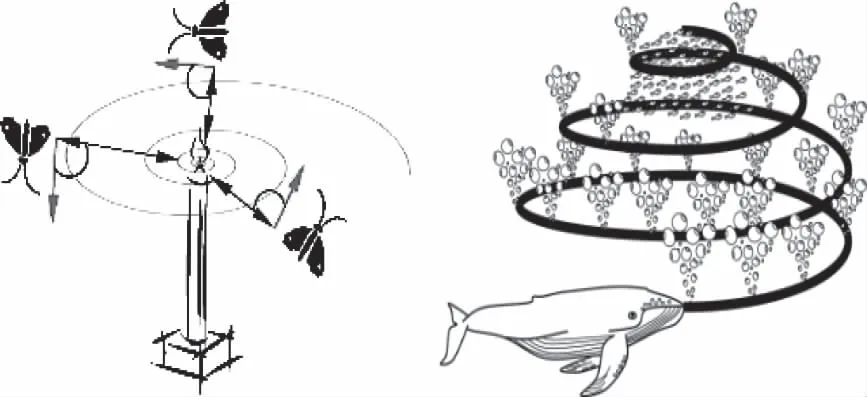
图2 飞蛾飞行路径 图3 座头鲸进食行为
Xt+1=|Xbest-Xt|×emn×cos(2πn)+Xbest
(17)
其中,Xbest表示最优解的位置向量,m表示对数螺旋常数,n表示路径系数,在WOA和MFO中m=1,n是(-1,1)之间的一个随机数。
受MFO和WOA算法中对数螺旋轨迹的启发,本文在1.3.1小节软围攻和1.3.2小节硬围攻中加入一种对数螺旋因子,来增强算法的局部开发性能,位置更新公式如下
X(t+1)=δ×(ΔX(t)-E|J×Xb(t)-X(t)|)
(18)
X(t+1)=δ×(Xb(t)-E|ΔX(t)|)
(19)
其中,δ=emn×cos(2πn)表示对数螺旋因子,m和n同WOA和MFO中的数据保持一致。
引入对数螺旋因子后,哈里斯鹰群将以对数螺旋飞行的方式去逮捕猎物,不容易被局部最优值所困,扩展了算法的局部搜索技术,增强了ELSHHO算法的定位能力,有效提高收敛速度和寻优精度。
3.3 ELSHHO算法的流程图
综上所述,ELSHHO的流程图如图4所示。

图4 ELSHHO流程图
4 实验与结果分析
实验运行环境为Windows 10(64位)操作系统、Intel(R) Core(TM)i5-6200U CPU、2.40GHz主频、4G 内存,算法在MATLABR2018b编程和运行。
4.1 参数设置
参数设置见表1。

表1 参数设置
4.2 测试函数
本文选用10个国际上通用的基准测试函数来测试ELSHHO的性能。如表2所示,其中f 1-f5为单峰函数,故常用来测试算法的开发能力,f6-f 10为多峰函数,故用来检验算法的探索能力和避免局部最优的能力,所有基准函数的维度为30,理论最优值为0。

表2 基准测试函数
4.3 ELSHHO与其它元启发式算法的比较分析
为了验证ELSHHO的有效性与优越性,本节选择PSO[18]、GWO[19]、MFO[16]、WOA[17]、以及传统 HHO[2]进行对比分析。为保证实验的公平性,各算法的共有参数设置同4.1节一致,其它参数设置和原文献一致,记录最优值、平均值、标准差,测试结果见表3,其中寻优结果最好的值用粗体表示。
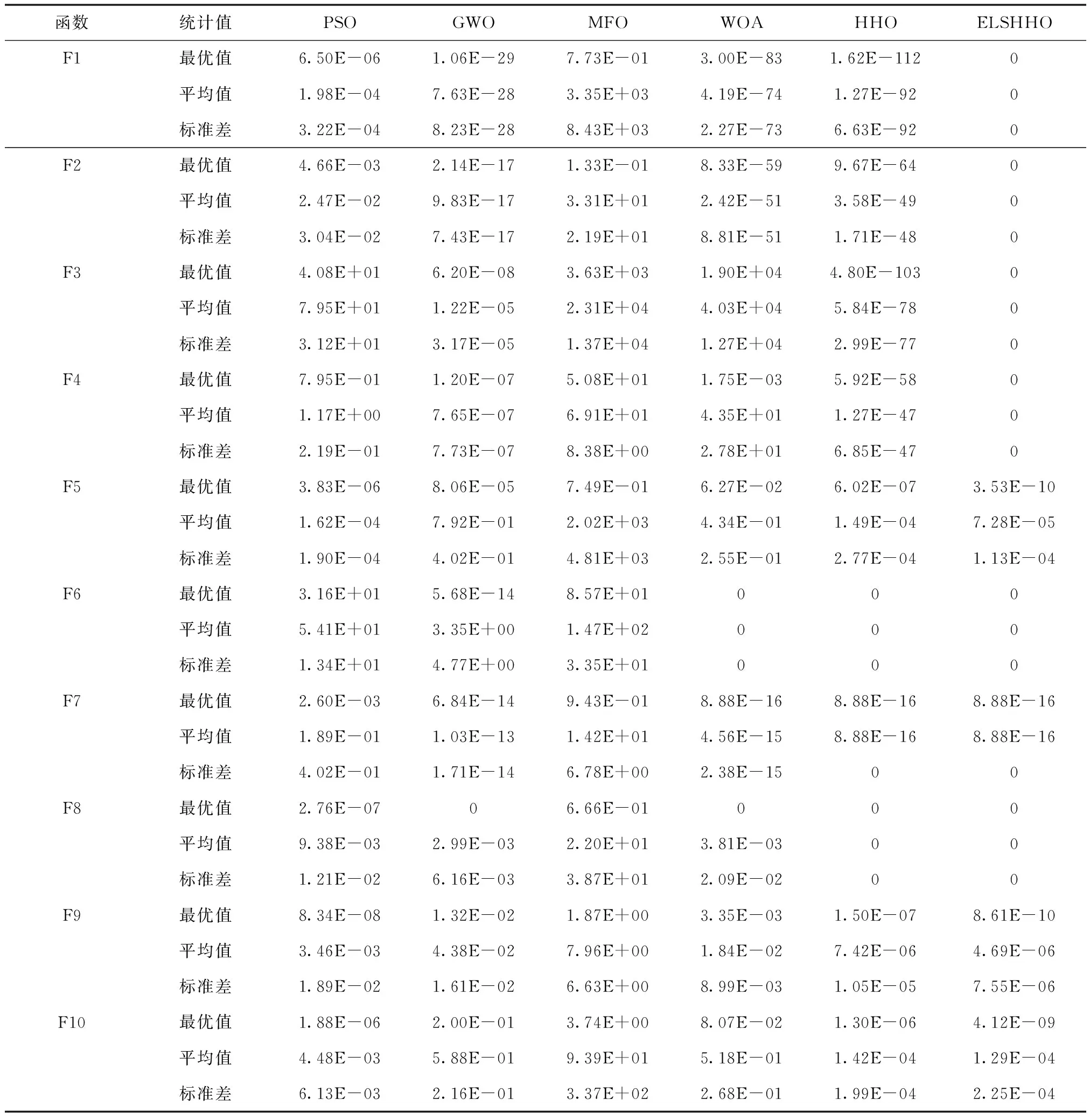
表3 ELSHHO与其它元启发式算法的测试结果比较
由表3可知,本文所提出ELSHHO的寻优能力明显优于PSO、GWO、MFO、WOA、HHO。对于函数F1-F4,ELSHHO可以直接搜索到最优值,寻优效果大幅度优于所有对比算法。对于函数F5、F9、F10,所有算法的均值相近,但ELSHHO的最优值略优于其它算法,这表明改进的算法对问题空间的探索和开发更加充分。对于函数F6,ELSHHO、HHO、WOA均能搜索到最优值,性能优于PSO、GWO、MFO。对于函数F7,ELSHHO与GWO、WOA、HHO的值相差不大,略优于PSO、MFO。对于函数F8,ELSHHO、HHO均能搜索到最优值,性能优于PSO、GWO、MFO 、WOA。10个基准测试函数中,除了函数F5、F9、F10,ELSHHO在其余7个函数上的标准差均为0,这表明ELSHHO具有较强的稳定性。以上实验结果分析证明,所提出ELSHHO有较强的寻优性和稳定性。
为了进一步阐述ELSHHO的收敛性能,给出部分基准函数的收敛曲线图,如图5所示。

图5 测试函数的收敛曲线图
从函数F1-F3的收敛曲线图可直观的看到ELSHHO的收敛速度和收敛精度都明显优于PSO、GWO、MFO、WOA、HHO。从函数F6可以看出,虽然ELSHHO、HHO、WOA的搜索精度一样,但ELSHHO的收敛速度快于HHO、WOA。对于函数F7,虽然ELSHHO与GWO、WOA、HHO的寻优精度旗鼓相当,但是ELSHHO的收敛速度快于其它算法。对于函数F8,ELSHHO在迭代50次之前就已经收敛到最优值,HHO在迭代200次之后才收敛到最优值,虽然两者的搜索精度一样,但ELSHHO比HHO的收敛速度更快。
4.4 ELSHHO与其它改进HHO算法的比较分析
为了验证ELSHHO与其它改进HHO算法的优劣性,本文选择与CHHO[8]、THHO[9]、LMHHO[10]、IHHO[11]进行对比分析。各算法的共有参数同4.1节一致,其它参数设置和原文献一致,对比结果见表4,其中“-”表示原文献中没有出现的。

表4 ELSHHO与其它改进的HHO算法的测试结果比较
如表4所示,ELSHHO在函数F2、F3、F4的最优值、平均值和标准差大幅度优于其它4种改进的算法。对于函数F1,ELSHHO、LMHHO的寻优精度相同,比CHHO、THHO、IHHO仍有巨大优势。对于函数F6-F8,因为5种算法都是在HHO的基础上改进而来,故性能指标一致。对于函数F5、F9、F10,所有改进算法相差不大,但ELSHHO的性能略优于其它改进算法。结果表明,ELSHHO算法的精确度和稳定性整体上优于其它4种改进的HHO算法。
5 结论
本文提出一种基于精英反向学习和对数螺旋的改进哈里斯鹰算法(ELSHHO)来克服传统哈里斯鹰算法的不足并进一步提升HHO算法的性能。在初始种群和每次种群迭代时都引入精英反向学习机制,提高种群的多样性和种群的质量。在开发阶段,引入对数螺旋因子来帮助种群进行局部搜索,指引种群更新位置,提高寻优性能。并通过10 个基准函数进行测试,将ELSHHO算法与其它5种元启发式算法和4种改进的HHO算法进行对比分析,实验结果表明,ELSHHO算法的收敛速度和解的精度较原始算法有了较大提升且优于绝大部分对比算法。

