基于神经网络的OFDM系统信道估计方法

陈佳勇,徐 湛,职如昕,田 露

(北京信息科技大学信息与通信工程学院,北京 100101)

1 引言

正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)技术作为长期演进(Long Term Evolution,LTE)的关键技术[1],能够很好地对抗频率选择性衰落和窄带干扰。OFDM将循环保护间隔(Cyclic Prefix,CP)添加到OFDM符号前,能够有效地抵抗衰落信道造成的符号间干扰[2](Inter Symbol Interference,ISI)。

信道估计是OFDM系统中非常重要的环节。信道估计的目的是估计出信道的冲激或者频率响应,在此基础上对接收数据进行校正和恢复,以准确的恢复出发送信号。传统的信道估计准则有最小二乘[3](Least square,LS)、最小均方误差[4](Minimum mean square error,MMSE)和最小线性均方误差[5](Linear Minimum mean square error,LMMSE)。LS估计算法不需要先验信息,只需要一次简单的除法运算,计算量小容易实现,但是由于忽略了噪声导致估计性能在信噪比较低时大大降低。MMSE估计算法考虑了信道的统计特性,需要对信道自相关矩阵求逆,计算量较大。

随着人工智能的不断发展,人们开始着眼于将深度学习应用于信道估计。文献[6]将OFDM系统和无线信道视为黑盒子,直接利用接收数据通过深度神经网络(DNN)恢复出发送数据,证明了DNN具有记忆和分析无线信道复杂特性的能力。文献[7]提出了一种简化的神经网络模型来进行信道估计和信号检测,降低了复杂度。文献[8]提出了一种模型驱动的深度学习方法,采用逐块信号处理,将接收端划分为信道估计子网和信号检测子网,每个子网由一个DNN构建,在计算复杂度和内存占用方面有优异的表现。文献[9]提出了一种在线训练数据的模型结构,训练过程更快,所需的训练数据大大减少。

上文提到的几种利用神经网络进行信道估计的方法插入的导频图案都是块状导频或者梳状导频。本文采用的导频图案是梳状导频的一种变种,分奇偶OFDM符号在频域上插入两种样式的导频。这种导频图案在对抗时间选择性衰落和频率选择性衰落有较为综合的表现[10]。针对导频图案的特殊结构,利用两个神经网络模型分别对奇偶OFDM符号进行训练和估计。由于神经网络的输入为导频处的频率响应,输出为数据处的频率响应,可以将预测的过程看作是频域插值,对比其它的插值方法如线性插值以及DFT插值,本文提出的方法表现更好。此外,由于奇偶符号的导频位置不一致,本文提出的双模型方法优于只用单一的神经网络模型同时训练奇偶符号的效果。

2 系统模型

OFDM的系统模型框图如图1所示,整个OFDM系统分为发射机与接收机两部分。首先是发射机,数据进行循环冗余校验(CRC),信道编码,打孔,交织,星座映射,插入导频并进行子载波加扰后进行反向傅里叶变换(IFFT),然后加入循环前缀(CP)形成OFDM符号进行传输。接收端则进行发射端的逆过程,在去除CP之后进行傅里叶变换(FFT),经过信道估计环节对其进行均衡,解调等操作后就可以恢复出发送的数据。

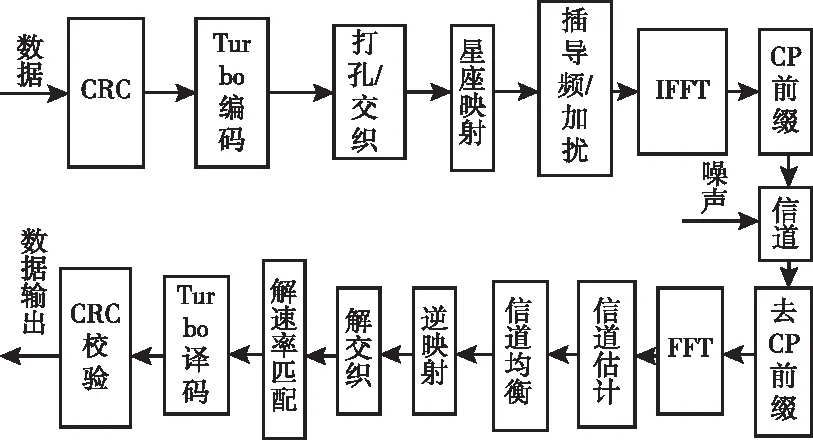
图1 OFDM系统框图

本文采用的导频图案如图2所示,可以看出,这种导频图案交错的在频域上的不同位置插入导频。这样的导频结构可以弥补梳状导频在频域上只对固定位置的符号进行估计的不足,使得估计的结果更为精确。

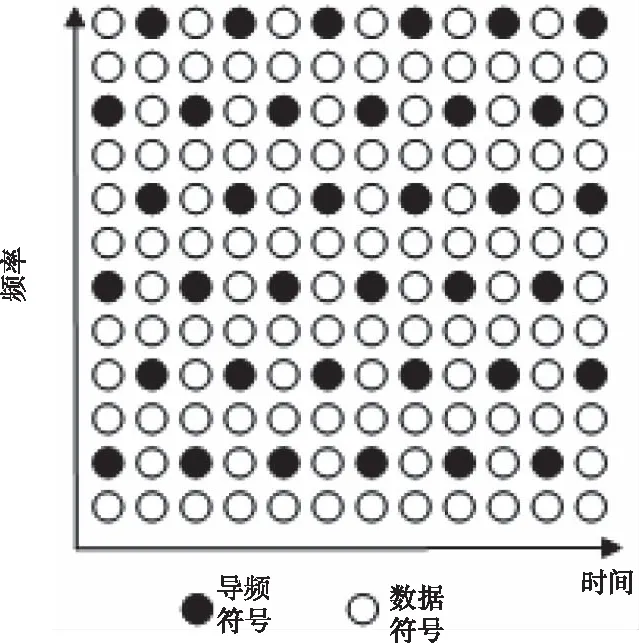
图2 奇偶交错的导频图案

OFDM信号在经过多径信道以及噪声干扰后,接收机得到的信号的频域形式可以表示为

Y(k)=H(k)X(k)+N(k),k=0,1…N-1

(1)

其中H(k)为第k个频点上的信道响应,X(k)为发送的符号,N(k)为加性高斯白噪声。

为了获取信道的准确信息,需要对其进行估计,传统的信道估计方法有LS和MMSE,这两种方法都是借助于导频实现的,LS算法可以表示为

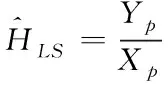
(2)

其中Yp和Xp分别是接收端和发送端的导频符号,可以看出,LS信道估计就是在频域上将接收导频与对应的发送导频相除,实现简单,但是在估计过程中没有考虑接收信号中的噪声,其估计精度将随着噪声的增大而降低。

MMSE算法可以表示为

MMSE=Ch(Ch+σ2I)-1LS

(3)

其中Ch表示信道的协方差矩阵,I表示单位矩阵,σ2表示噪声方差。

MMSE方法在估计中加入了信道的二阶统计特性,所以估计更加精确,但是由于需要对矩阵进行求逆,计算复杂度显著增加。并且在实际应用中,信道的噪声和协方差矩阵是无法获得的,因此在实际通信中难以实现。

3 基于神经网络的信道估计

人工神经网络不需要提前确定输入输出之间的映射关系,而是通过自身的训练,经过大量的学习过程,在给定输入值时可以得到最接近期望输出值。BP神经网络是一种按误差反向传播训练的多层前馈网络,其算法称为BP算法,它的基本思想是梯度下降法,利用随机梯度下降算法或者批量梯度下降算法,使网络的实际输出值和期望输出值的误差均方差达到最小。本文将神经网络模型应用于信道估计,将由导频估计得到的频率响应作为神经网络的输入,经过隐藏层的非线性映射,将神经网络的输出作为整个OFDM符号的频率响应用来进行信道均衡。

3.1 神经网络结构

本文使用的神经网络模型由输入层、隐藏层和输出层组成,每层神经元的数量分别为32,30,224。本文使用的模型只有一层隐藏层,较多的隐藏层虽然对估计精确度有所提升,但却加大了计算的复杂度。BP算法的基本的学习过程由信号的正向传播与误差的反向传播两个过程组成。

首先是正向传播,输入层接收到的输入数据为经过LS估计得到的导频位置处的频率响应LS,由于频率响应为复数,所以需要提取其实部LS＿re与虚部LS＿im进行组合后送入输入层

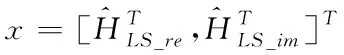
(4)

输入向量与输入层和隐藏层之间的权重矩阵相乘后与偏置项相加作为隐藏层的输入

u(1)=W(1)x+b(1)

(5)

其中,W(1)和b(1)分别为输入层与隐藏层之间的权重矩阵与偏置向量。

接着在非线性激活函数的作用下,隐藏层将结果输出进入输出层

x(1)=f(u(1))

(6)

同理可以得到整个神经网络模型的输出为

x(2)=f(W(2)f(W(1)x+b(1))+b(2))

(7)

将输出层输出的结果进行重新组合成复数的形式便可以得到由神经网络预测的数据符号处的频率响应。

其中,隐藏层的激活函数为Sigmoid函数,其公式可以表示为

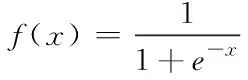
(8)

由于信道频率响应的值是有正负的,而Sigmoid函数的输出范围为[0,1],所以输出层的激活函数选择Tanh函数,其输出范围为[-1,1],公式可以表示为

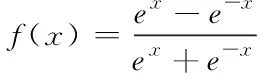
(9)

反向传播时,计算损失函数对各层之间的权重矩阵与偏置向量的偏导数后采用梯度下降算法对其进行迭代更新,使损失函数朝着神经网络输出与实际信道响应之间误差极小值的方向进行优化。

3.2 神经网络模型训练和估计过程

基于神经网络的信道估计算法由训练和估计两部分组成,其训练过程如图3所示。

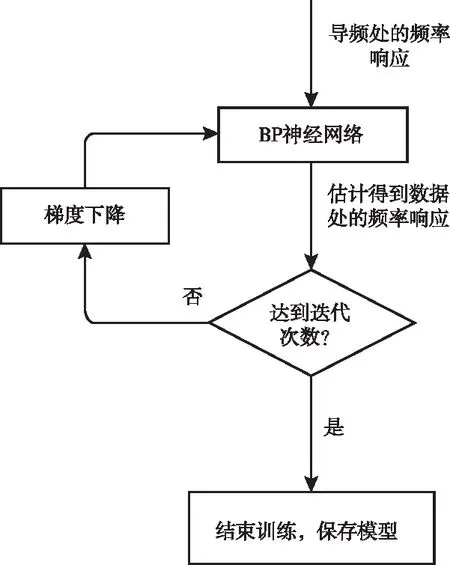
图3 神经网络训练过程

首先,分别提取出奇偶OFDM符号,对其去除CP,再进行FFT。由于奇偶符号的导频位置不同,需要分别将其导频符号提取出来并进行LS估计得到频率响应Hp＿odd和Hp＿even,然后将其分别作为奇偶模型的输入进行训练,由于奇偶符号的信道估计的训练和估计过程是一样的,因此图4展示的训练流程对奇偶符号都适用。本文将实际的信道响应H作为训练标签样本,损失函数选用的是L2 loss,可以将其表示为

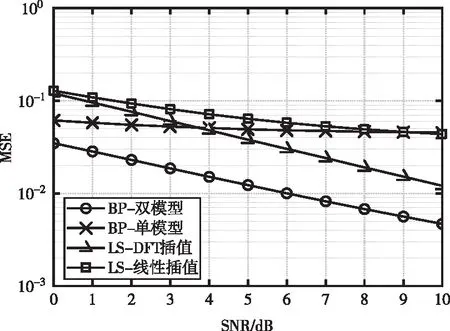
图4 不同信道估计方法的信道响应MSE

(10)

本文将神经网络的所有参数采用高斯分布进行初始化,训练过程的学习率设置为0.5,梯度下降算法选用的是小批量梯度下降,从训练数据集中每次选取1000个样本对参数进行更新,本文将训练的epoch设置为200。

训练完成后的模型即可用来进行信道响应的在线估计。分别将奇偶符号经过LS估计得到的频率响应送入对应的神经网络模型,将输出作为数据处的频率响应进行信道均衡,将接收数据恢复成发送数据。

4 仿真结果

本文提出的方法实际上相当于在LS估计后进行频域插值,所以本节将本文方法与线性插值和DFT插值进行比较。此外由于本文的方法分奇偶两个模型进行训练,所以将本文的方法与单神经网络模型估计的性能进行比较。比较的性能指标为信道响应的均方误差(MSE)和系统误码率(BER)。其中MSE可表示为

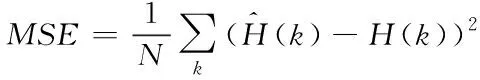
(11)

仿真参数如表1所示。

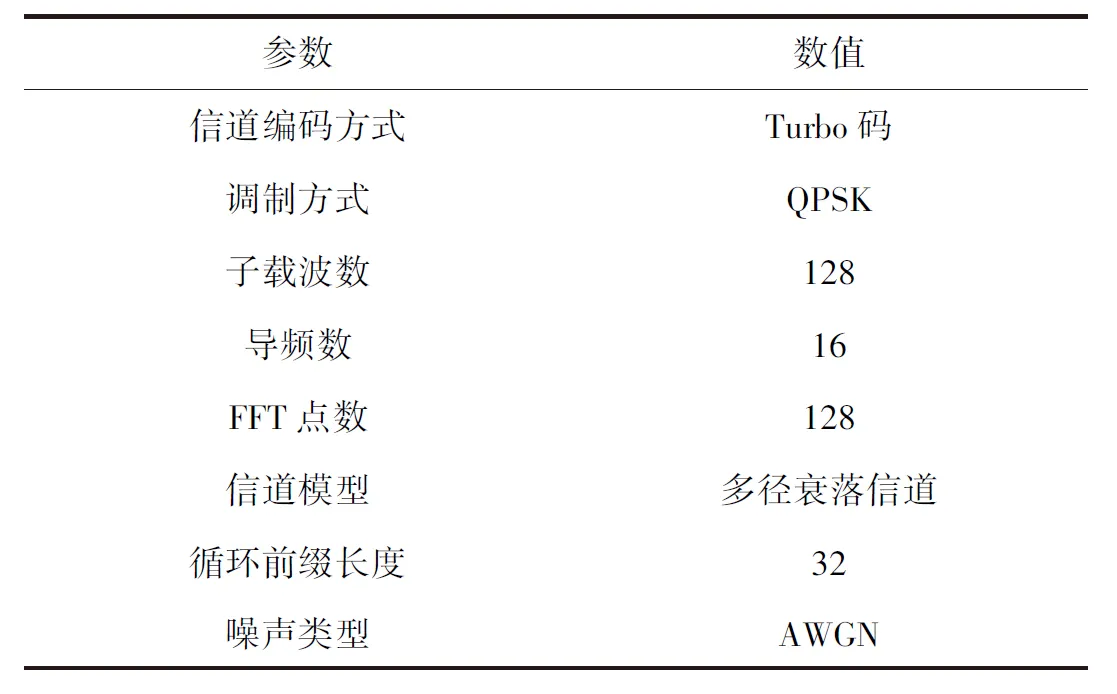
表1 仿真参数设置

由图4可以看出,线性插值虽然实现简单,但是当导频间较大时,线性插值便不能有效的描绘出导频间信道响应的变化,由于本文实验设置的导频间隔为8个频点,因此线性插值在估计信道响应时表现较差。而DFT插值是将根据导频估计得到的频率响应做一次IFFT得到时域冲激响应,在时域上进行去噪,再经过时域补零,相当于频域插值,接着做FFT变换到频域得到完整的频率响应。由于DFT插值在时域有去噪的操作,因此对信道的估计效果较线性插值略微提升。但由于其无法有效去除循环前缀范围之内的噪声,因此仍无法获得较好的估计性能。对于单神经网络模型,由于导频图案的特殊性,导致该方法无法兼顾到奇偶符号的差异性,因此无论是低信噪比还是高信噪比下,都无法很好地对信道进行有效的估计。而本文提出的奇偶双模型方法将奇偶符号进行拆分,分别对其进行估计,因此可以弥补单模型方法的上述缺陷。同时神经网络能够将导频处的信道信息经过复杂的非线性映射得到整个符号完整的信道信息。可以利用先验的信道信息对神经网络模型进行训练,使其可以学习到信道的变化特征,在低信噪比情况下也能有效地学习噪声对信道的影响。可以看出其估计得出的信道响应均方误差比DFT插值有3-4dB的性能提升。

由图5可以得知,线性插值由于不能很好的描述信道信息,此方法系统误码率最高。单神经网络模型虽然在低信噪比时信道估计效果比线性插值好,但由于此时的数据本身含有噪声,因此信道均衡时效果同样较差,而高信噪比时单神经网络模型的MSE已经与线性插值持平,所以在误码率性能方面也与线性插值几乎保持一致。虽然DFT插值较前面两种方法已经有所提升,BER随着信噪比的提高有明显的下降趋势,但本文提出的奇偶双模型的方法能够通过训练有效地学习无线信道的状态变化与噪声对信道的影响,因此其性能比DFT插值仍有2dB左右的提升。

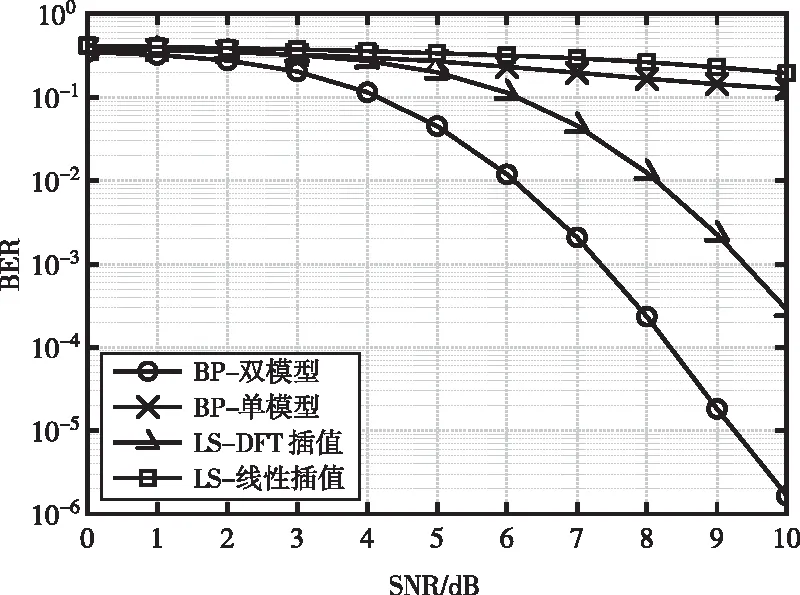
图5 不同信道估计方法的系统误码率

5 结束语

本文针对奇偶交错的导频图案,提出了用两个神经网络模型与信道估计相结合的方法,分别对奇偶OFDM符号进行训练和估计,并进行了仿真验证。实验表明,本文提出的方法与线性插值以及DFT插值等方法相比,无论是信道响应的均方误差还是系统误码率均有数dB的提升。此外,与单神经网络模型相比,本文提出的双模型方法在各方面表现都要更佳。因此,本文提出的基于神经网络的信道估计方法性能良好且复杂度适中。