基于局部色彩传递的多帧影视图像扭曲校正

刘珈吟,金 凤

(1. 武汉设计工程学院,湖北 武汉 430060;2. 国防科技大学信息通信学院,陕西 西安 710106)

1 引言

近年来,在图像处理领域中多帧影视图像的校正颇受关注,而常规灰色图像因其过于匮乏的信息量[1],导致多帧影视图像的研究与使用无法更深入。相对于灰色图像而言,彩色图像不仅具有更好的观赏价值,而且在细节和内容方面也更具优势。因此使多帧影视图像彩色化在多帧影视图像扭曲校正方面具有重要意义[2,3]。

参考图像到灰度图像的色彩传递是图像彩色化的重要环节。色彩传递分为全局传递和局部传递,相对于全局传递,局部色彩传递能够更好地保持图像的连贯性和区分性。为使多帧影视图像彩色化效果更佳,本文采用局部色彩传递方法中的Levin算法对多帧影视图像进行彩色化处理。

局部色彩传递方法虽然优于全局传递,但是忽略了局部纹理特性,常常导致局部颜色混合、边缘颜色越界等问题[4]。本文采用局部色传递的方法使多帧影视图像彩色化后,用双边过滤方法对图像进行优化,进而更好地完成多帧影视图像扭曲校正。采集图像后,对图像进行自适应结构元网格线交叉点坐标提取、Biharmonic样条曲面插值,实现对局部色彩传递的多帧影视图像的扭曲校正。

2 多帧影视图像扭曲校正

2.1 多帧影视图像色彩化

2.1.1 Levin算法

采用Levin算法实现多帧影视图像的局部色彩传递[5],其理念为若图像中像素的亮度值大致相同,那么像素的颜色值也大致相同。Levin利用这一基本原理创造了一种二次能量函数,通过求解这个函数实现灰色图像色彩化。这种方法以颜色线条理论为基础,因而要求用户必须提供初始颜色线条且此颜色是用户要得到结果的颜色点。通过求取每一个像素和其相邻像素的加权差、所有像素的平方和最小值进行颜色传递是Levin色彩传递的基本思想[6]。为了确保图像彩色化最佳,应该使得二次能量函数值最低,U、V是两种颜色通道的色度、饱和度,Y是亮度通道。通过Y的信息可以得到U、V的分布,改变的U、V与未改变的Y结合,通过数学推导,对U、V求解,可实现图像彩色化。

Levin算法应用时首先要确定最小目标函数

(1)

式中,灰色像素点r的颜色值用U(r)代表,它的一块领域用N(r)代表。U(s)表示第s个彩色化像素点的颜色值,归一化函数为Wrs,图像中全部灰色像素点用∑r()描述,归一化函数用Wrs描述,根据像素点r、s间的距离可以计算出归一化函数的值,前提是满足∑s∈N(r)Wrs=1。Wrs函数值越小,说明两个像素点颜色相似度越低,反之值越大颜色相似度也越高。

以两个亮度值平方差Wrsαe-(Y(r)-Y(s))2/2σr2为基础,其中Y(U)表示亮度值,第一步先将目标函数方程转化为式(2):

J(U)=(AU)TAU=UTATAU

(2)

式中,权值矩阵用A代表,UT表示图像速度分量转化成的列向量,表示如式(3)所示。将式(3)带入式(2)中,可将色度值的权重关系通过亮度值归结为式(4),同时为确保图像色彩化时人工标注色彩的稳定性还需要定义函数(5),式中b是代表原始信息的列向量。

UT=[u1,u2,…,un]

(3)

(4)

bTU=bTb

(5)

在满足式(5)的情况下,求解最终图像彩色化最优的问题实际上就是使式(1)所示的目标函数最小化,要想解决这个问题需要使用拉格朗日乘子,这时可求得最小化式(6),并对式(5)求导可得到式(7)

P(U)=UTAU+λ(bTb-bTU)

(6)

AU=b

(7)

式中,b是列向量bT=[b1,b2…,bn],A代表权值矩阵,U表示求解的颜色值转化矩阵,对这个方程进行求解可使图像的色彩化。

2.1.2 联合双边过滤的图像优化

Levin算法虽然能够通过图像分割处理使图像色彩化,但在图像边缘和纹理较弱区域中存在不稳定因素,使得图像色彩化有误差存在[7],因而在Levin算法的基础上,采用联合双边过滤技术对基于Levin算法的局部色彩传递多帧影视图像进行优化。优化处理流程示意如图1。

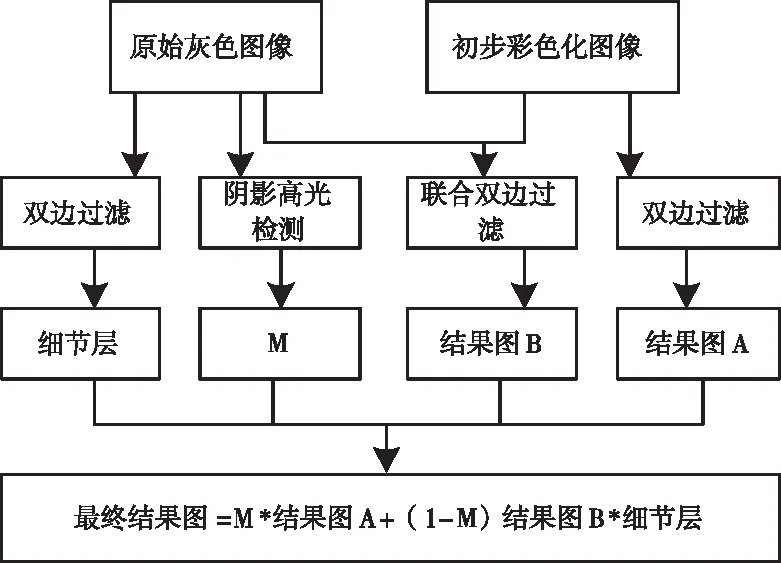
图1 优化处理流程示意图

1)双边过滤

采用双边滤波对图像像素周围的局部像素值进行加权平均处理,得到的二维高斯滤波则是图像的像素值[8]。像素距离目标像素距离与其价值度具有反比例关系。双边过滤算法依据高斯分布对初步彩色化图像的像素p进行计算,其计算如式(8),式(8)中的k(p)可表示为式(9)

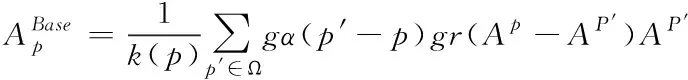
(8)

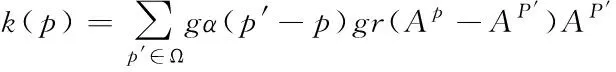
(9)

若想得到空间域的权重,需要通过高斯函数gα计算对像素间距离进行运算实现[9]。修正参数σα、σγ实现宽度值的修正。

2)联合双边过滤

把另一个图像加入到双边过滤值域的权重计算中就是联合双边过滤。把双边过滤权重计算中的初步彩色化结果替换成原始灰色图形,则像素的计算为式(10),k(p)变化为式(11)

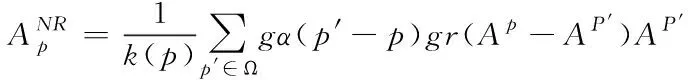
(10)

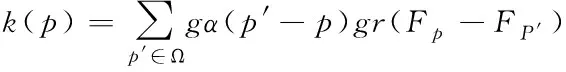
(11)

原始灰度图像几乎无噪声,因而把参数σγ设置成较小值可以保证边缘停止函数gr(Fp-FP′)选择正确权重。

3)细节传递

联合双边过滤对局部色彩传递的多帧影视图像虽然进行了优化,但是不能增加影视图像初步彩色化图像中的细节。相反的原始图像却能将更多表面细节呈现出来。为达到对原始图像细节进行传递的目的,先要用式(12)计算原始灰度图像的一个细节层

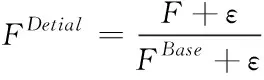
(12)

式中,FBase代表原始图像双边过滤结果。为了降低图像中某些信号值产生的影响,设置参数ε,计算各RGB通道的ε值,捕捉图像F的局部细节变化。从计算机视觉角度出发,一般将其叫作比值图像(商像)。将联合双边过滤图像乘以该比值图像AFinal,可实现细节传递。彩色化图像最终计算方法如下

AFinal=(1-M)ANRFDetial+MABase

(13)

其中,M为选择控制条件,在检测阴影、高光区域如果图像彩色化像素没出现,取值为0,否则为1。

2.2 图像扭曲校正

2.2.1 获取自适应结构元网格线交叉点坐标

1)膨胀与腐蚀

对图像进行处理要以膨胀、腐蚀为基础。其中图像中目标变粗、生长的过程就叫膨胀[10]。结构元素形状控制着目标的生长、变粗程度。膨胀公式可以定义为

A⊕B={z|()z∩A≠φ}

(14)

其中,结构元为B;φ是空集;A⊕B描述A被B膨胀。

为过滤原物体周围的边界点,要对图像进行腐蚀操作,同样的腐蚀公式可以定义为

E=B⊗S={x,y|Sxy⊆B}

(15)

其中,二值图像E是S腐蚀B形成的全部点(x,y)的集合;若B中含有全部的S,则要求S平移到点(x,y)。

2)结构元

结构元是膨胀、腐蚀最基本的部分。一般情况下,它具有以下特征:数值是1、0组成的矩阵;大小形状任意且小于处理的图像很多;原点指定待处理像素范围且数值为1的点决定膨胀、腐蚀时领域像素参与计算与否。

2.2.2 图像扭曲校正

Biharmonic样条曲面插值图像校正方法作为一种全局校正方法,它的优点是可灵活操作、整体平滑局部性能好,且对控制点的分布与数量无要求[11];便于实验者增加、删除特征点的数量和调整特征点位置。与其它全局方法的不同之处在于:插值结果具有最小曲率;不同维度的Biharmonic方程的解就是不同维度的Green函数;插值结果与不精确数据点不匹配。

用矩阵X2,Y2、x1,y1和四个列向量x1,y1、x2与y2存储多帧影视图像扭曲网格线交叉点横、纵坐标值。理想图像坐标值是(X2,Y2),提取的扭曲网格线交叉点横、纵坐标相对应的理想图像的交叉点坐标值(x2,y2)。之后用x1,y1、x2与y2拟合出x2=f1(x1,y1)、y2=f2(x1,y1)两个曲面。

在理想图像中,通过映射扭曲变形多帧影视图像的任意坐标就可以实现多帧影视图像的扭曲校正[12]。在校正多帧影视图像扭曲的过程中,需要不断输出和运算图像像素位置,因此该过程是一种向后映射过程。

差值X1、Y1矩阵需要通过Biharmonic样条曲面插值方法获取,两种矩阵同扭曲图像对应的坐标值分别是X2和Y2。通过双线性插值算法计算矩阵X1、Y1中的坐标点,得出图像校正后的像素灰度值。

3 实验与论证

3.1 数据采集

本文采用南京普爱射线影像装备有限公司的7200型号C臂CT机对多帧影视图像进行采集,C臂CT机参数如表1。

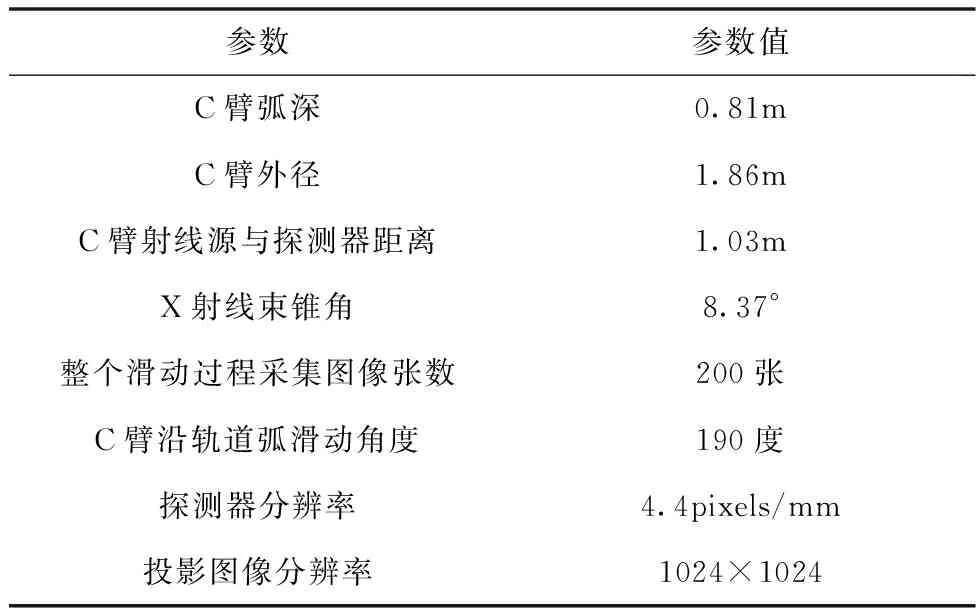
表1 C臂CT机参数

3.2 多帧影视图像彩色化验证

应用本文方法对多帧影视图像彩色化效果进行验证,图2、图3分别给出本文方法的两组实验结果图,其中图2中的图像为白天拍摄,图3中的图像为夜晚拍摄。图2(a)为白天拍摄到的初始颜色线条图,图2(b)是应用本文方法的Levin算法进行局部色彩传递得到的图像,图2(c)是应用本文方法的联合双边过滤优化得到的图像;图3(a)为夜晚拍摄得到的初始颜色线条图,图3(b)应用本文方法的Levin算法进行局部色彩传递得到的图像,图3(c)是应用本文方法的联合双边过滤优化得到的图像。

图2 白天拍摄图像

图3 夜晚拍摄图像

从图2和图3可以看出,对比初始颜色线条图2(a)、图3(a),本文应用Levin算法得到的多帧影视图像图2(b)、图3(b)不仅具有很好的观赏价值,而且在细节和内容方面也更具优势。但是通过Levin算法得到的多帧影视图像局部色彩存在模糊现象,降低了图像视觉效果;而本文方法应用联合双边过滤优化得到的多帧影视图像图2(c)、图3(c)图像更清晰,不存在局部色彩模糊现象,处理结果较为理想,视觉效果也更佳,说明本文方法的多帧影视图像彩色化效果显著,彩色化处理后图像细腻,视觉效果更加理想。

3.3 扭曲校正验证

3.3.1 交叉点坐标提取结果

应用本文方法对C臂CT机采集的图像进行实验,交叉点坐标提取步骤见图4。从中可以看出通过提取膨胀结构元以及腐蚀结构元,可以得到网格交叉点坐标。其中膨胀结构元是交叉点临近两组网格线宽度均值的25%,而腐蚀结构元是膨胀后网格交叉点两组网格线宽度均值的50%。

图4 坐标提取过程

分析图4可知,从采集到原始图像(a)可以看出,图像中网格线存在明显的扭曲现象,扭曲程度较重。图4(b)是膨胀时正方形结构元边长是4、腐蚀时正方形结构元边长设置成8提取的结果。从图4(b)可看出,膨胀时若结构元边长过小,会导致部分区域腐蚀过度,无法提取所需交叉点;图4(c)是膨胀时将正方形边长设置成5、腐蚀时将正方形边长设置成8提取的结果。同样从图4(c)可看出,膨胀时结构元边长设置过大,腐蚀后还能看到某些网格线。图4(d)是用自适应结构元处理得到的结果。从图4(d)可看出应用本文方法的网格交叉处充满了要提取的点,说明本文方法应用坐标提取算法,能有效保留网格交叉点,可有效提取图像坐标,为图像扭曲校正提供可靠依据。

表2是应用本文方法的两种交叉点坐标提取结果。

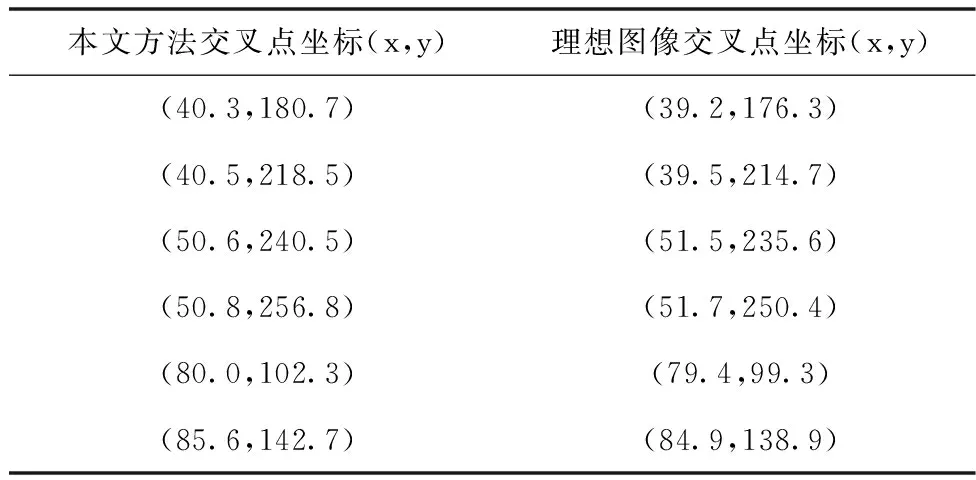
表2 交叉点坐标

从表2可以看出,采用本文方法的自适应结构元提取的网格交叉点坐标精度域理想交叉点坐标之间的误差极小,完全可满足图像扭曲校正时所要求的控制点坐标值精度。

3.3.2 图像扭曲校正

采用本文方法应用的Biharmonic样条插值方法对图4(a)进行图像扭曲校正,得到的校正结果见图5。

图5 图像校正结果

从图5分析可得,原始图像中扭曲的网格线已经明显变直,验证了本文方法对局部色彩传递的多帧影视图像扭曲校正的可行性。

4 结论

本文提出基于局部色彩传递的多帧影视图像扭曲校正方法,应用Levin算法和联合双边过滤方法对多帧影视图像原始灰度图像进行局部色彩传递及优化,在此基础上,采用Biharmonic样条多帧影视图像扭曲校正方法,通过自适应结构元网格线坐标提取网格线交叉点坐标,并用Biharmonic样条对局部色彩传递的多帧影视图像扭曲校正。经实验验证,本文方法的多帧影视图像彩色化处理效果好,且能够通过提取交叉点坐标有效校正局部色彩传递的多帧影视图像。