多仓库物流周期联合配送粒子群择优算法仿真
龚艳茹,马立坤
(1. 北京科技大学天津学院,天津 301830;2. 北京科技大学机械工程学院,北京 100083)
1 引言
物流[1]作为企业交流过程中不可或缺的重要组成部分,其配送方案与经济合理性已成为彰显企业竞争力及企业管理能力的重要象征。物流配送之所以能够在世界范围内有效流通,不仅是因为其实现了现实物品网络运输的理想化服务状态,还因为其现代化的经营理念对传统商贸领域产生了巨大的冲击和影响,使现代物流[2]更加信息化、现代化、社会化。由此可见,优化物流配送能力是企业提升自身市场竞争力的关键所在。
王勇[3]等人通过计算物流成本和配送损失成本建立物流成本模型,并在该模型中输入基于K-means聚类算法获取的商品配送温控子集和客户时间窗约束条件,使物流成本模型优化成双目标优化模型,优化后的模型不仅能够提供商品最优配送方案,还能根据商品配送时间分析物流敏感度,实现物流配送方法的优化,该方法存在物流配送时间过长的问题。李存兵[4]等人通过自适应遗传聚类算法获取物流配送过程中的方差最小化距离,再将方差最小化距离与不同服务区域的最大化物流分布指标相结合,构成物流系统综合优化模型,将变异算子改进的遗传算法输入该模型中,使物流系统综合优化模型的收敛速度显著提升,实现物流配送方法的优化,该方法存在物流配送时间过长的问题。王晓丽[5]等人通过分析配送商品与物流资源数据的关系特征,建立基于大数据背景下整合计算流程简便的物流配送链优化模型,该模型能够实时分析物流配送链信息,获取最佳配送路径,实现物流配送方法的优化,该方法存在物流配送距离过远的问题。
为了解决上述方法中存在的问题,提出多仓库物流周期联合配送粒子群择优算法。
2 建立物流配送优化模型
2.1 选择优化目标
在实际的物流运输工作中,能够影响物流配送成本[6]的主要因素是实际运输量和车载率,若从虚拟的理想视角分析物流配送成本,则与其相关的实际运输量和车载率在运输成本取值最小时对运输成本的影响程度可以忽略不计,若从现实视角分析物流配送成本,则与其相关的实际运输量和车载率在运输成本取值最小时对运输成本的影响主要以油耗量、载重量、时间窗[7]、行驶速度等向量形式体现,由此可见,优化目标的选择可以通过提取物流配送成本的最小能耗参数,进而获取实际运输量和车载率基于油耗量、载重量、时间窗、行驶速度的最优向量指标。
由于物流配送成本与物流配送距离成线性关系,即物流配送成本越低,物流配送距离越近,因此在提取物流配送成本最小能耗参数的过程中,需要协同考虑两因素对于最小能耗参数的影响。利用Bekats方程计算物流配送的最小成本,再利用行驶公式计算物流配送的最小距离,此时的实际运输量和车载率均表现为阈值范围内的最优向量指标,可以通过解码算法[8]和预选择策略[9]分别获取实际运输量最优向量指标和车载率最优向量指标。Bekats方程的表达式如下
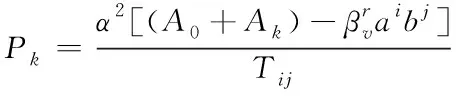
(1)
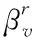
行驶公式的表达式如下
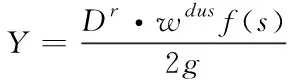
(2)
式中,Dr表示行驶公式的常数;wdus表示物流配送距离的计算误差;2g表示物流配送距离的取值区间;f(s)表示物流配送成本对物流配送距离的影响系数。
解码算法的表达式如下
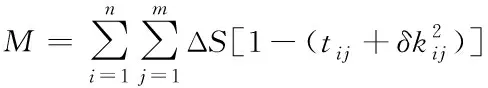
(3)
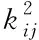
预选择策略的表达式如下
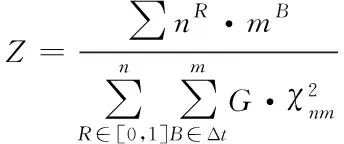
(4)
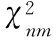
在成功获取实际运输量和车载率的最优向量指标后,将该指标数据输入自适应差分进化算法[10]中,提取基于最小能耗参数的物流配送成本,完成优化目标的选择。自适应差分进化算法的表达式如下

(5)
式中,∂表示自适应交叉常数;kavg表示参与交叉算法的实际运输量最优向量指数;xavg表示参与交叉算法的车载率最优向量指数;kx表示最小能耗参数的提取误差;U表示满足优化目标最终选择的物流配送成本最小能耗参数。
2.2 建立基于优化目标的物流配送优化模型

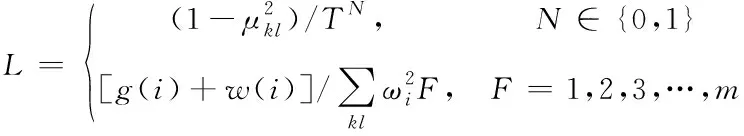
(6)
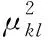
物流配送模型的表达式如下
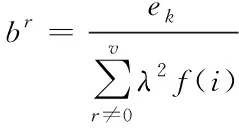
(7)
式中,r表示物流配送中心的总数;ek表示物流配送的正确率;f(i)表示物流配送的错误率;λ2表示客户对任意服务区的物流配送业务满意度。
物流配送优化模型的表达式如下

(8)
3 粒子群择优算法
3.1 收敛性条件
利用粒子群择优算法对物流配送优化模型迭代求解,获取基于物流配送优化模型的加速参数,进而提升整体物流配送业务的性能,首先要设立收敛性条件,限制物流配送优化模型的收敛性,达到简化模型计算复杂度的目的。收敛性条件的设立过程如下:首先通过FastICA算法[12]消除模型内重叠特征多项式,降低模型迭代难度,再利用虚拟消去法[13]获取模型初始条件决定的加速因子,并计算该因子在迭代过程中的加速度,将加速度惯性权重输入多维空间内,获取基于配送物流优化模型的收敛性条件。FastICA算法的表达式如下
(9)
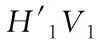
虚拟消去法的表达式如下

(10)

收敛性条件的表达式如下
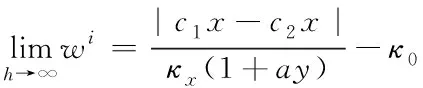
(11)
式中,c1x-c2x表示物流配送优化模型的收敛极限;ay表示收敛条件对物流配送优化模型的简化参数;κ表示物流配送优化模型计算复杂度的最小阈值。
3.2 粒子群择优算法求解物流配送优化模型
物流配送优化模型经过收敛条件的限制,其计算复杂度得到大幅度降低,对后续模型求解工作具有重要意义。利用粒子群择优算法求解物流配送优化模型的具体操作步骤如下:首选利用二维粒子行为矢量获取物流配送优化模型基于物流配送成本与物流配送损耗之间的最优平衡状态,再将该平衡状态系数输入参数自调整粒子群模型中迭代,根据模型迭代输出的加速参数,实现物流配送优化模型的求解,该加速参数不但能够最大限度减少物流配送过程中造成的能源、经济损耗,还能拉近客户与物流配送企业之间的关系,实现真正意义上的双面共赢。
二维粒子行为矢量是指在粒子矢量图中引入二维向量,通过观察物流配送优化模型经过二维向量运算后所得的粒子轨迹[14]在粒子矢量图中的偏移方向,获取物流配送优化模型基于物流配送成本与物流配送损耗之间的平衡状态。二维向量表达式如下

(12)
式中,Δp表示二维向量权重值;ei表示向量学习因子;sinv表示二维向量结合粒子群的权重系数。
粒子矢量图如下图1所示。
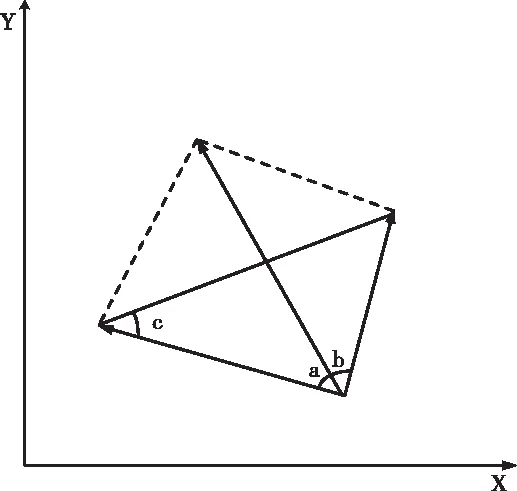
图1 粒子矢量图
图1中的矢量角a表示为a={p1·o1};矢量角b表示为b={p2·o2};矢量角c表示为c={p3·o3}。
在物流配送优化模型中输入二维向量,并将获取的粒子轨迹记录在粒子矢量图中,通过观察粒子矢量图中粒子轨迹的偏移方向,获取物流配送优化模型基于物流配送成本与物流配送损耗之间的平衡状态。粒子矢量图中粒子轨迹的偏移方向如下图2所示。
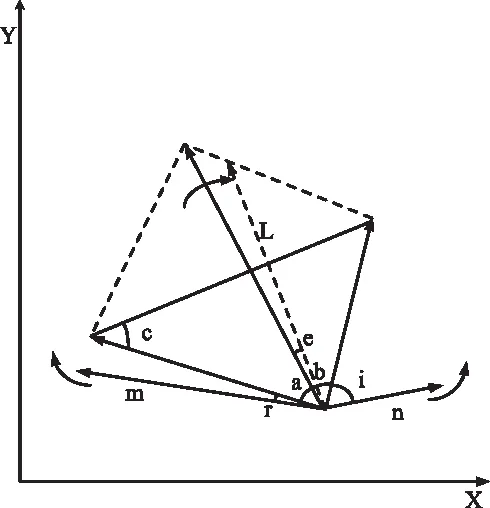
图2 粒子矢量图粒子轨迹的偏移方向
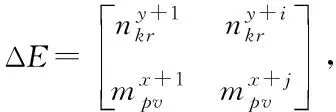
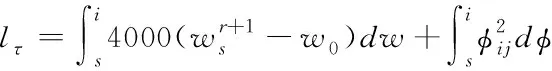
(13)
将物流配送成本与物流配送损耗之间的平衡状态系数输入参数自调整粒子群模型中迭代,获取物流配送优化模型的加速参数。参数调整粒子群模型的表达式如下

(14)
式中,σ表示参数自调整常数;xy表示粒子群迭代次数;P′表示加速参数输出误差;ik表示物流配送成本与物流配送损耗之间的平衡系数值对该模型迭代速度的影响;B(α)表示基于物流配送优化模型的加速参数。
4 实验与分析
为了验证多仓库物流周期联合配送粒子群择优算法仿真的整体有效性,需要对其测试。
选择a、b、c三组规模不同的物流服务区作为实验对象,a组客户数为3000,服务区配送面积为2公顷;b组客户数为1000,服务区配送面积为1公顷;c组客户数为5000,服务区配送面积为3公顷。规定上述三组物流服务区为实验对象,分别采用不同方法优化物流配送方法,对比不同方法基于三组物流服务区的时间缩短量和距离缩短量,进而推测不同方法的物流配送优化性能。
1)配送时间缩短量
分别采用所提方法、文献[4]方法和文献[5]方法优化物流配送方法,并将优化后的物流配送方法分别应用于a、b、c三组规模不同的物流服务区中,通过对比不同方法的物流配送时间,总结不同方法的时间缩短量。不同方法的物流配送时间如图3所示。

图3 不同方法的物流配送时间
由图3可见,所提方法优化物流配送方法后,a组物流配送时间不超过40h,b组物流配送时间不超过10h,c组物流配送时间不超过20h,说明所提方法在a、b、c三组规模不同的物流服务区内的物流配送时间都出现大幅度下降,即物流配送的时间缩短量明显,这是因为所提方法通过提取物流配送成本的最小能耗参数,建立基于优化目标的物流配送优化模型,使得物流配送在时间方面表现出极高的优越性。文献[4]方法优化物流配送方法后,a组物流配送时间超过60h,b组物流配送时间超过15h,c组物流配送时间超过20h,说明文献[4]方法在a、b、c三组规模不同的物流服务区内的物流配送时间下降并不明显,即物流配送的时间缩短量并不明显。文献[5]方法优化物流配送方法后,a组物流配送时间超过80h,b组物流配送时间超过30h,c组物流配送时间超过50h,说明文献[5]方法在a、b、c三组规模不同的物流服务区内的物流配送时间下降幅度较小,即物流配送的时间缩短量较小。经上述对比可知,所提方法优化物流配送方法后,其时间缩短量明显优于传统方法。
2)配送距离缩短量
分别采用所提方法、文献[3]方法和文献[4]方法优化物流配送方法,并将优化后的物流配送方法分别应用于a、b、c三组规模不同的物流服务区中,通过对比不同方法的物流配送距离,总结不同方法的距离缩短量。不同方法的物流配送距离如图4所示。
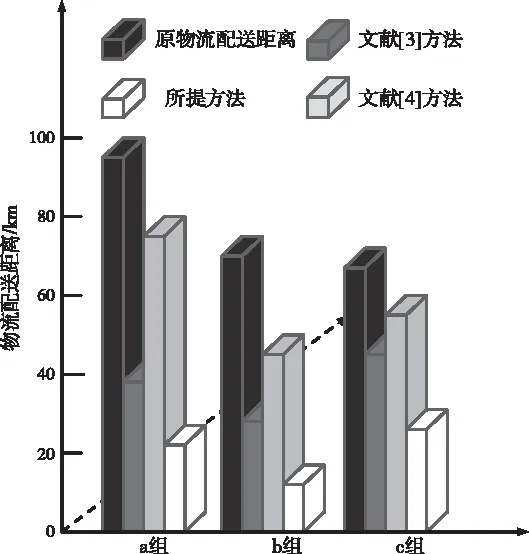
图4 不同方法的物流配送距离
由图4可见,所提方法优化物流配送方法后,a组物流配送距离不超过30km,b组物流配送距离不超过20km,c组物流配送距离不超过40km,说明所提方法在a、b、c三组规模不同的物流服务区内的物流配送距离都出现大幅度下降,即物流配送的距离缩短量明显。文献[3]方法优化物流配送方法后,a组物流配送距离超过35km,b组物流配送距离超过20km,c组物流配送距离超过40km,说明文献[3]方法在a、b、c三组规模不同的物流服务区内的物流配送距离下降并不明显,即物流配送的距离缩短量并不明显。文献[4]方法优化物流配送方法后,a组物流配送距离超过70km,b组物流配送距离超过40km,c组物流配送距离超过50km,说明文献[4]方法在a、b、c三组规模不同的物流服务区内的物流配送距离改善情况较差,即物流配送的距离缩短量较差。经上述对比可知,所提方法对物流配送优化后,不仅能够择选出最优配送路径,缩短物流配送的距离,还能提高物流配送效率,有助于提升客户对物流配送业务的满意度。
5 结束语
传统的物流配送工作存在物流配送时间长、物流配送距离远的问题,提出多仓库物流周期联合配送粒子群择优算法仿真的方法,最大限度减少物流配送过程中由于时间过长、距离过远而造成的经济损失。如何在保证物流配送全面优化的同时,实现物流配送过程中包裹、货物的实时监控,提高包裹、货物的安全性是研究人员下一步工作的重点。

