基于分区匹配和MBAS-RFR的定位算法

陈平安,孙运全,张超虎

(江苏大学电气信息工程学院,江苏 镇江 210031)

1 引言

截止2018年年底,我国已探明煤炭储量居全球第三位,尽管我国煤矿安全开采水平逐渐提升,但煤矿事故时常发生[1],为了提高煤矿井下安全生产水平、减少煤矿事故带来的人员财产损失,因此需要进一步研究井下人员定位技术。

目前井下人员定位技术大多基于射频识别(Radio Frequency Identification,RFID)技术开发,但存在精度低的问题,而基于接受信号强度指示[2](Received Signal Strength Indication,RSSI)的定位技术功耗小,成本低,近年来获得了大力发展及推广,在基于RSSI的定位方法中,位置指纹定位无需测距,该方法通过建立RSSI与位置坐标的非线性映射关系来推断出待定位点的位置坐标。适合井下复杂环境中定位。近年来基于位置指纹[3]定位算法已有大量研究,宋明智[4]等将遗传算法与随机森林相结合,解决了奇点问题;余修武[5]等将巷道分区,以信号强度确定其大致区域然后利用PSO算法定位,但在信号强度波动性大的情况下可能会存在误判情况;赵建国[6]等逐步缩小待定位点的定位区域,最后利用KNN算法实现最终定位,提高了定位速度,但不适合于指纹库较小的场景;崔丽珍[7]等采用粒子群算法优化神经网络,建立了RSSI和位置的非线性关系。吴雪敏[8]等通过RSSI判断判断待测节点所属区域,然后利用改进鸡群优化算法实现具体定位,提高了定位精度,但电磁信号具有波动性,粗定位阶段判断所属区域会出现误判进而影响后续定位精度。

以上研究表明智能优化算法可有效提高模型精度并且利用区域划分思想应用于井下人员定位中可有效缩小定位范围,改善定位效果。本文提出了一种基于分区匹配和MBAS-RFR的井下人员定位模型,首先根据AP节点对井下巷道划分区域,将离线指纹库中符合条件的指纹数据作为每个区域的中心参考点,利用改进加权欧氏距离结合余弦相似度模型综合判断待定位点的所属区域,最后通过MBAS(Multitask Beetle Antennae Swarm,多任务天牛群)-RFR(Random Forest Regression,随机森林回归)模型进行具体定位。

2 MBAS-RFR算法实现

2.1 随机森林回归

随机森林(Random Forest,RF)算法是Breiman提出的一种以装袋法(Bagging)为核心思想的集成算法[9],由多个决策树组成,随机森林回归(Random Forest Regression,RFR)即是由多棵回归树组成的一种用于回归问题预测的算法,它克服了决策树容易过拟合的问题,具有回归性能好,训练速度快等优点。

2.2 BAS算法

天牛须搜索(BAS,Beetle Antennae Search)算法是Jiang等[10]人提出的一种新型高效的智能优化算法,天牛须搜索算法原理实际是天牛觅食的过程。天牛须搜索算法具体过程如下:

1)设置天牛朝向,天牛的朝向向量是随机的

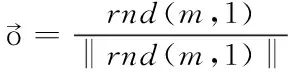
(1)

2)根据天牛朝向计算天牛左右须的位置

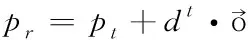
(2)

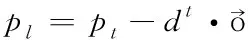
(3)

3)计算左右须气味浓度函数值并进一步更新天牛的位置

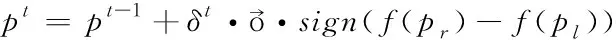
(4)

4)更新天牛左右须间距和搜索步长

dt=0.95·dt-1+0.01

(5)

δt=0.95·δt-1

(6)

2.3 MBAS算法

多任务天牛群算法(MBAS,Multitask Beetle Antennae Swarm)是一种借鉴了人工蜂群(ABC,Artificial Bee Colony)算法中蜂群结构并结合了天牛须搜索算法(BAS)的启发式算法[11],该算法原理如下:定义种群数量为N的天牛群,天牛群分为三种任务类型,分别是搜索者,追随者以及探索者,对于搜索者来说,任务是在可行解集内找到最优解,根据天牛须搜索算法寻优,位置更新如式(7)所示

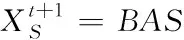
(7)

追随者天牛跟随搜索者天牛,寻找当前全局最优解周围的潜在的最优解,位置更新如式(9)所示

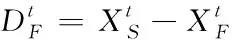
(8)

(9)

式(9)中,LF是追随者的搜索步长。

探索者天牛以固定步长移动,防止系统陷入局部最优,如式(11)所示

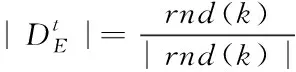
(10)

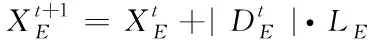
(11)

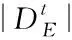
当达到最大迭代次数后,终止寻优,输出全局最优解。

MBAS算法实现了从单只天牛寻优到群体天牛寻优的转变,并且将天牛群分成不同任务类型进行高效寻优,极大程度克服了单只天牛寻优易陷入局部最优的不足,改善了算法的稳定性及寻优效果。

2.4 MBAS-RFR算法

MBAS-RFR算法基本思想是利用MBAS算法对RFR的参数进行寻优,对RFR算法影响最大的参数主要为决策树数量以及树深度,因此利用MBAS算法上述参数进行迭代寻优。具体流程如下:

1)初始化MBAS算法参数,设置种群数sizepop,最大迭代次数T,追随者、探索者搜索步长等。

2)将优化目标RFR得出的定位平均误差作为天牛个体适应度值,如式(13)所示

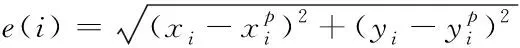
(12)

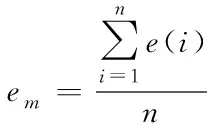
(13)

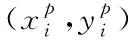
3)计算天牛个体适应度值,将个体按适应度值升序处理,适应度最小个体为当前最优个体。

4)将天牛群体分为三种任务类型,按适应度升序排列依次为搜索者、追随者、探索者。

5)根据相关公式分别对追随者搜索者探索者群体进行方向和位置上的更新

6)分别计算三类天牛群体的适应度值

7)判断当前最小适应度值与上次迭代最小适应度值大小关系,从中选取当前最优个体。

8)重复步骤3)至步骤7)直至最大迭代次数结束。

9)将MBAS算法输出的最优解作为RFR最优参数,同时用对应训练集样本训练RFR,建立井下定位算法模型。

3 改进分区匹配模型

在具体定位前,首先需要根据AP节点对井下巷道进行等距离分区,如图1所示,其中,Bb、Cc、Dd、Ee将巷道分为五个等距区域并从离线数据中选出每个区域的中心点,在线阶段,通过衡量待定位点的信号强度与中心点信号强度的相似度特征,将待定位点进行分区,分区匹配效果的好坏直接关系到具体定位阶段的定位效果,一般采用欧氏距离模型衡量两个n维向量的距离大小[12],但在实际的井下巷道环境中电磁环境容易受到多径效应以及非视距因素等干扰,传统欧氏距离分区匹配模型会受到一定程度影响,因此,应针对井下复杂环境对欧氏距离分区匹配模型进行适当改进。

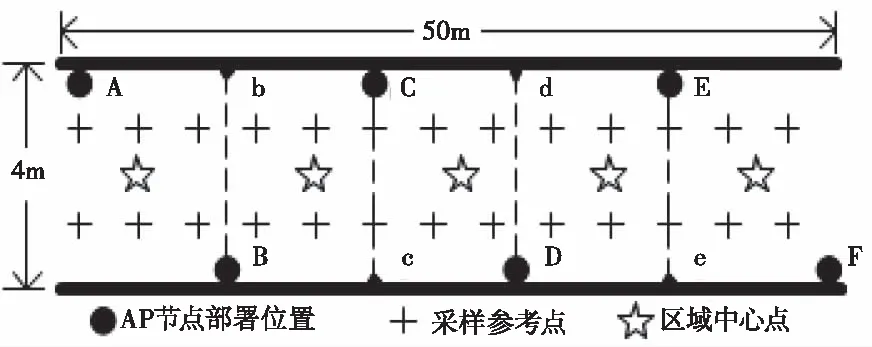
图1 井下巷道模型

3.1 改进加权欧氏距离模型

受井下环境影响,井下巷道电磁信号波动较大,波动较大的信号数据所表示的实际位置不稳定,故应该增大实际计算出的欧式距离来表达不稳定度,方差反映了数据的波动性,故将多次测量的信号强度数据取方差处理,将方差引入到欧式距离计算中去。故改进欧氏距离模型如式(14)所示

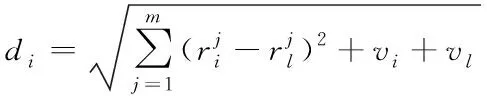
(14)

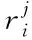
图1所示井下巷道中,待定位节点采集的信号强度来自均匀分布的6个AP节点,巷道分区并选出区域中心点后,此时可利用改进欧氏距离公式来判断待测点与中心点的相似度,从而判断出待定位点所属区域,但分区匹配模型存在不足,因为未考虑每个AP节点对待定位点的影响程度,距离AP节点越近,信号越强;因此可以通过判定所测信号强弱来判断待定位点所处的大致区域。故本文提出一种可变权重的欧氏距离公式,可根据信号强度大小判断待定位点所在大致区域,进而对此间区域改进欧式距离的计算进行适当加权处理,可变权重欧氏距离公式如(15)所示

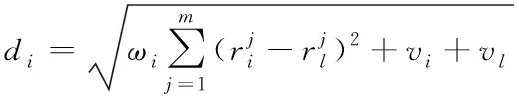
(15)

式中,ωi表示权重值,根据AP节点相邻程度改变,ωi具体取值如下:

1)当信号强度特征最强三个对应AP节点为相邻关系时

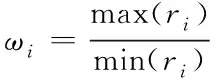
(16)

式中,max(ri)为某测试点中的最强信号强度特征,min(ri)为某测试点中的最弱信号强度特征。

2)当最强信号特征的前两个对应AP节点为相邻关系且最强信号特征前三个对应AP节点仅横跨三个区域时

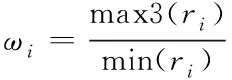
(17)

式中,max3(ri)是ri中降序排列第三的信号强度特征。

3)其它

ωi=1

(18)

3.2 余弦相似度模型

余弦相似度通过向量的内积空间夹角余弦值来衡量向量之间的相似性程度,余弦值越接近1,两个向量越相似[13]。余弦相似度模型如式(19)所示

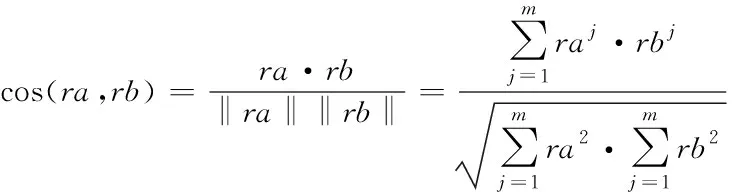
(19)

3.3 改进加权欧氏距离结合余弦相似度

针对单一模型分区匹配衡量指标不全面导致精度不理想的问题。本文在前人研究基础[14]上将改进后的欧氏距离模型与余弦相似度模型结合如式(20)所示

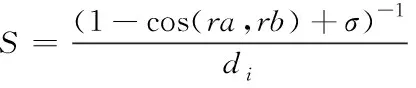
(20)

式中,di为改进加权欧氏距离,cos(ra,rb)为余弦相似度。σ是一个随机较小值,防止分母为0。

由式(20)可知,当两个向量的改进加权欧氏距离越小并且余弦相似度值越大时,此时改进分区匹配模型值越大,说明两个向量之间的相似度越高。

4 井下定位算法流程

本文算法流程有两个阶段,首先离线阶段多次采集指纹数据取均值,准备好位置指纹库,根据AP节点来划分井下巷道区域,每个区域的定位模型训练数据采用本区域和相邻区域部分训练集数据,建立MBAS-RFR算法定位模型。

在线阶段,利用改进加权欧氏距离结合余弦相似度模型将接收到的实时位置指纹数据与中心参考点进行匹配,将实时位置指纹数据进行分区处理,然后,在每一个区域中,利用MBAS-RFR定位模型根据待定位点RSS数据计算出对应位置坐标。算法流程如图2所示。

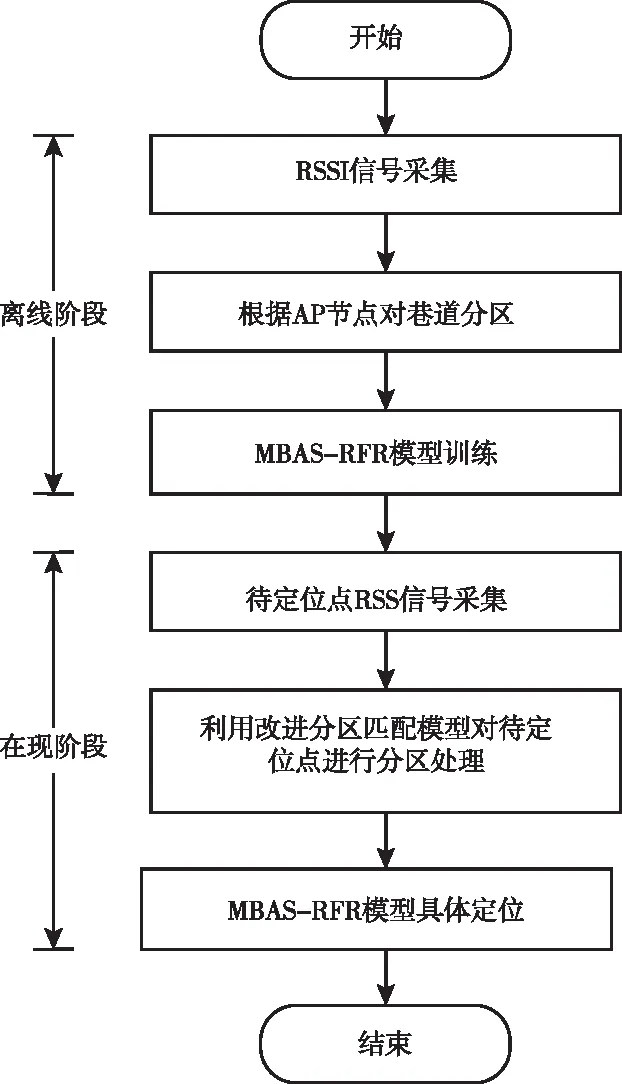
图2 本文算法流程图

5 实验分析

5.1 实验设计

本文采用射线跟踪法[15]-[17]模拟井下巷道信号模型,生成训练测试用的位置指纹数据,实验平台基于Python语言搭建,电脑配置为Core i5处理器、8GB内存。利用ITU传播模型来模拟井下信号衰减变化,如式(21)所示

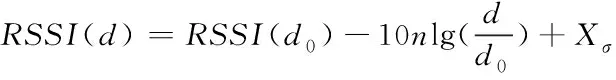
(21)

式中,d为AP节点和待测节点的实际距离;d0为参考距离,RSSI(d0)为参考距离接收到的信号强度指示;Xσ是均值为0的高斯随机噪声,n为信号衰减指数。多次测量信号强度数据取均值构建位置指纹数据库包括693组离线训练数据、50组在线测试数据,部分训练数据见表1。

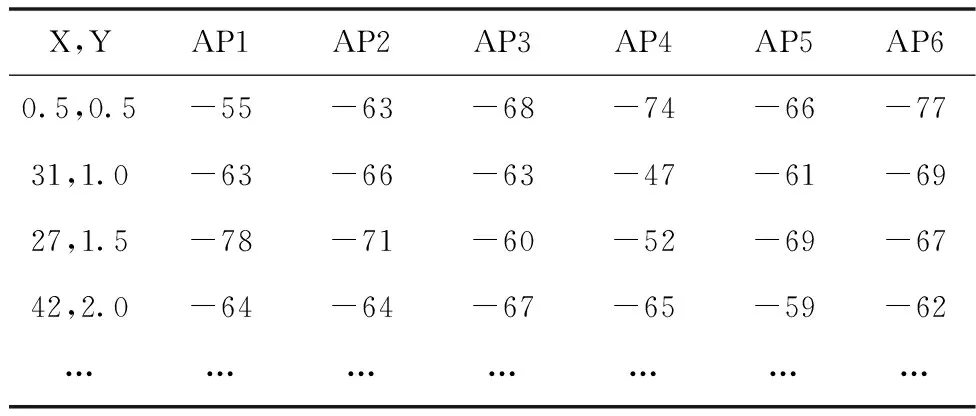
表1 部分训练数据(信号强度单位:dBm)

实验模拟50m×4m的井下巷道模型,在其中均匀分布六个AP节点。巷道通过AP节点划分区域并在每个区域随机分布测试点数据,如图3所示。

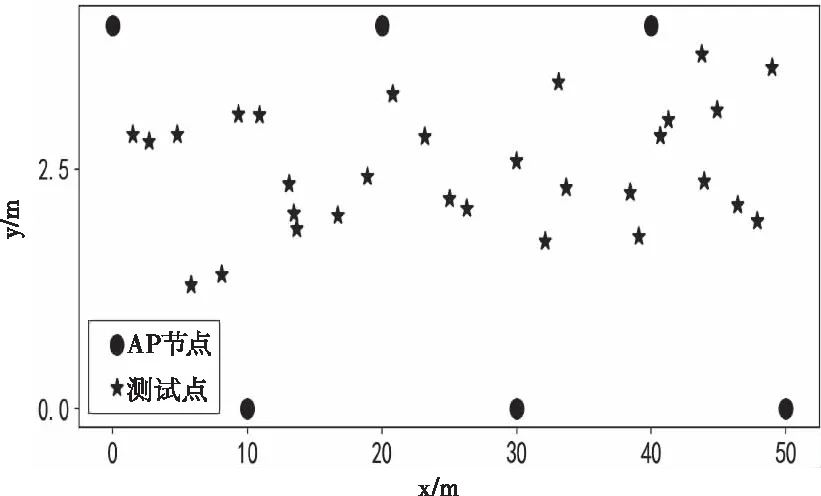
图3 巷道测试模型

实验主要内容是加入MBAS优化算法前后三种定位模型性能对比。对定位模型性能的评判指标为平均定位误差和不同距离误差距离下的置信概率。

5.2 MBAS算法加入前定位模型性能评估

为了能直观地展示本文提出的定位算法性能,使用同样的训练数据和测试数据代入不同定位模型。并对其结果进行对比分析,其中包括随机森林回归(RFR),欧氏距离分区匹配模型结合随机森林回归(E-RFR)和改进分区匹配模型结合随机森林回归(IE-RFR)。使用的数据是在同一环境中采集的测量数据。部分定位结果图4所示。

图4 优化前定位模型性能对比图

根据图4、表2分析,结合了分区匹配算法的两种定位模型平均误差分别降低了20.33%和26.97%,这说明了分区匹配模型能够有效降低定位误差;其中,相比于E-RFR定位模型,IE-RFR算法模型定位误差最小,定位精度更高,这说明本文提出的改进分区匹配算法分区匹配效果更好,更有利于保证后续阶段的定位精度。

表2 优化前定位模型平均误差

图5分析可知,IE-RFR算法在误差1.5m以内置信概率为62%,而E-RFR和RFR则分别为54%和38%,进一步说明了IE-RFR算法相比另外两种模型定位精度更高。

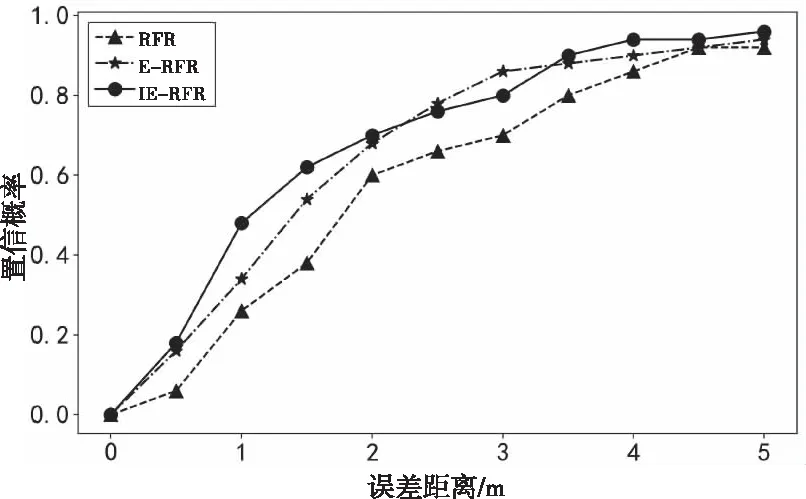
图5 优化前定位模型置信概率对比

5.3 MBAS算法加入后定位模型性能评估

相较于未加入优化算法前,由图6和表3分析可知,三种定位模型的平均误差均有所降低且定位波动性降低;这说明了MBAS优化算法提高了定位模型的稳定性并降低了定位误差;相比于另外两种模型,本文算法的平均定位误差分别降低了29.22%及15.76%,且定位稳定性最好。

表3 加入优化算法后定位模型平均误差

图6 加入优化算法后模型性能对比

图7分析可知,本文算法在误差1.5m内的置信概率是66%,而EMBAS-RFR和MBAS-RFR定位模型分别只有56%和60%,本文算法在1.5米内的准确率要高10%和6%,这说明改进加权欧氏距离结合余弦相似度模型结合MBAS-RFR定位模型具有更好的定位精度和定位稳定性且该定位精度能够满足井下人员定位要求。

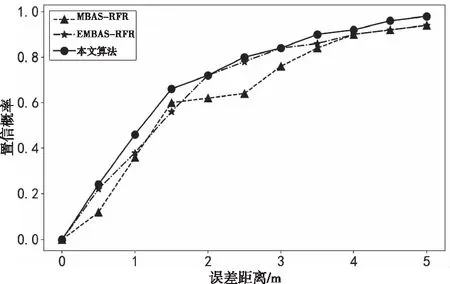
图7 定位模型性能对比图

6 结论

针对井下环境复杂以及电磁信号波动导致井下人员定位精度低的问题,本文提出了基于分区匹配和多任务天牛群优化随机森林的井下人员定位算法。首先使用改进加权欧氏距离结合余弦相似度的分区匹配模型对待定位节点进行分区处理,随后利用MBAS-RFR算法进行具体定位,本文分区匹配算法保证了后续具体定位阶段的精度,有效降低了定位误差,多任务天牛群算法有效的提高了定位的稳定性和精度。下一步将研究不同巷道类型对于定位精度的影响及模型优化。