水下压缩气体储能管道振动特性分析

梁成玉, 熊 伟, 王美玲, 王志文

(大连海事大学 船舶与海洋工程学院, 辽宁 大连 116000)

引言

“碳达标”和“碳中和”的提出,对我国的能源结构变革意义重大。然而,自然地质条件是限制我国规模化能源储存面临的卡脖子问题。水下压缩气体储能为突破当前规模化气体能源储存发展提供了补充性思路。在水下输气管道内经常因低温高压的条件,伴随着水蒸气的析出和积聚,进而使得管道内形成气液两相流现象。因液体的产生加剧输气管道内腐蚀且存在水击风险,同时压力流量波动会诱导管道振动以及调压设备等湍振。反过来,管道振动又会对管内两相流流动产生影响,进一步加剧压力流量波动,因此对管道进行流固耦合分析有着重要的意义[1-3]。

国内外研究者针对管道流固耦合做了大量研究。从经典水锤理论到水击理论的发展[4],其关于流体的非定常振荡会引起管道的振动得到了充实的证明。在此基础上,管道的振动也会引起流体运动状态的改变,即两者之间存在耦合振动。在进行了大量理论研究与实验之后,SREEJITH B等[5]对高速加压流体管道的振动问题建立了流固耦合的运动动力学有限元方程,以管内流速为变量,进而验证了模型的正确性,并将其应用于核反应堆管道系统。

于家付等[6]对载流管道的振动系统进行了阐述,并在此基础上推导了振动方程,分析方程并提出了输流管道的减振措施。马璐[7]在ANSYS-Workbench中对弯曲输流管道分别进行了单向流固耦合与双向流固耦合分析。从分析中可知,双向耦合作用下弯管最大等效应力与最大变形量均大于单向耦合。同时,弯管固有频率在双向流固耦合下明显降低,且固有频率随壁厚和管径的增大呈非线性增长。徐凯等[8]建立了管道流固耦合的有限元模型,并研究了管道结构、内流场及其流固耦合下的模态。从结果中可知,管道内流场的模态振型呈对称分布,耦合下的模态振型大部分与管体结构较为类似。李青等[9]在ANSYS-Workbench中建立了输油弯管的三维模型,通过改变流速和压强进而分析在流固耦合作用下管道的振动频率和应变。对比流体流速,流体压力对振动频率影响大。而同样是对速度和压力变化影响振动频率的研究,李明华等[10]做了管道在无流固耦合和单向流固耦合的固有频率和振型对比。结果可知,单向流固耦合作用下的固有频率与无流固耦合状态相差8%～10%,且无流固耦合下的形变量比单向流固耦合的变形增加了5%。

1 理论分析

1.1 模态分析

模态分析是用于确定结构固有频率和振型的一种线性分析方法,除了边界位移约束外,无其他载荷。

管道振动微分方程[11-14]:

(1)

假设管道只有自由振动,并忽略阻尼,即:

C=0,f(t)=0

(2)

结构系统和无阻尼自由振动方程为:

(3)

式中,M—— 管道质量矩阵

K—— 管道刚度矩阵

u—— 管道节点位移向量

由微分方程的一般理论可知,无阻尼自由振动方程的基本解形式为:

u(t)=φsin(ωt+α)

(4)

式中,φ为非零的n元列矢量,并且其各个分量与时间t无关,ω和α为待定常量,将式(4)代入式(3)中可得:

(K-ω2M)φsin(ωt+α)=0

(5)

满足上述方程的条件是:

(K-ω2M)φ=0

(6)

得到一个关于φ的线性齐次方程,它由非零解的充要条件式系数矩阵的行列式为零,即:

|K-ω2M|=0

(7)

(8)

ωi对应的φ为结构的振型,即假定结构以频率fi振动时的形状。

1.2 流固耦合

流固耦合是研究流场与固体之间相互作用的一种方法[15-18]。在管道内流体的流动会使管道结构发生变形,反之,变形的管道结构也会对管内流场作用。而输流管道内的流固耦合是否发生与管内流体的静压和动压相关。当流体静压与动压小于管道的临界载荷时,管道的固有频率变化并不大,进而不会发生流固耦合。而当管道临界载荷与流体的静压与动压接近时,管道的固有频率与流体产生的频率相接近,输流管道将会发生共振现象,这种现象对管道的危害极大,会引起管道的疲劳损坏。此时管道便会发生流固耦合振动。

从研究方法上,流固耦合可以分为单向流固耦合与双向流固耦合。单向流固耦合是将流体与固体分别建立,将流体的计算结果以载荷的形式导入到固体场内。这种作用是单向的,因而只能研究流体对固体的作用,不考虑固体对流体的影响。而双向流固耦合是考虑流体对固体以及固体对流体两个相互作用。Workbench中对输流管道的流固耦合分析是通过流固交界面,流场对结构的作用可传到固体场进行分析,固体场的形变也会传到流体场进行分析。

2 管道流固耦合模态分析

2.1 仿真方法

管道内流固耦合的仿真分析方法分为单向流固耦合与双向流固耦合。在本研究中,管道为玻璃材质且因积液运动而产生的管道结构方面的变形量较小,其对内部流场的影响较小,故而本研究只考虑了流场对管道结构的影响,进而选择单向耦合进行计算。

通过ANSYS-Fluent对管内流场进行分析,并将流场的分析结果输入到Static Structural模块,以压力形式作用在管内壁面上,再将其计算结果导入Modal模块内,进行模态分析。

2.2 几何参数

通过ANSYS中的建模模块,建立丘陵型管道模型如图1所示,模型参数见表1,管道底部有一定体积量的积液,空气从管道左侧通入。

表1 管道模型参数Tab.1 Pipeline model parameters

图1 管道模型图Fig.1 Pipeline model diagram

2.3 材料参数

管道采用石英玻璃,其弹性模量为7.2×1010Pa,密度为2203 kg/m3,泊松比为0.17。空气密度为1.225 kg/m3,动力黏度为1.81×10-5Pas。水的密度为998.2 kg/m3,动力黏度为1.004×10-3Pas。

2.4 网格划分

管内有流体域和固体域,分别对两部分进行网格划分。流体域划分时,对模型里的固体采取抑制,采用4面体网格划分流体域,并插入膨胀层,膨胀层选择8层,其网格划分结果如图2所示。同样,固体域网格划分时,对模型内的流体域进行抑制,如图3所示。由于管道较长的长度,网格总量为996191。

图2 流体域网格划分Fig.2 Fluid domain meshing

图3 固体域网格划分Fig.3 Solid domain meshing

2.5 流固耦合模态分析流程

Workbench中,管道进行流固耦合模态分析的常用模块是Fluid Flow(Fluent),Static Structural,Modal,三者按照图4的顺序连接。

图4 流程图Fig.4 Flow chart

管内的流动并不是单相流动,需要进行积液量的设置。在Fluent软件中,针对管内气液两相流动问题,气相为主相,液相为第二相,使用Adapt指定管道内积液区域为初始时刻液相的区域分布。在初始化之后,进行Patch指令,对Adapt设置的区域设置为第二相。设置好参数后,进行计算,待结果收敛后进行分析。其结果收敛图如图5所示。

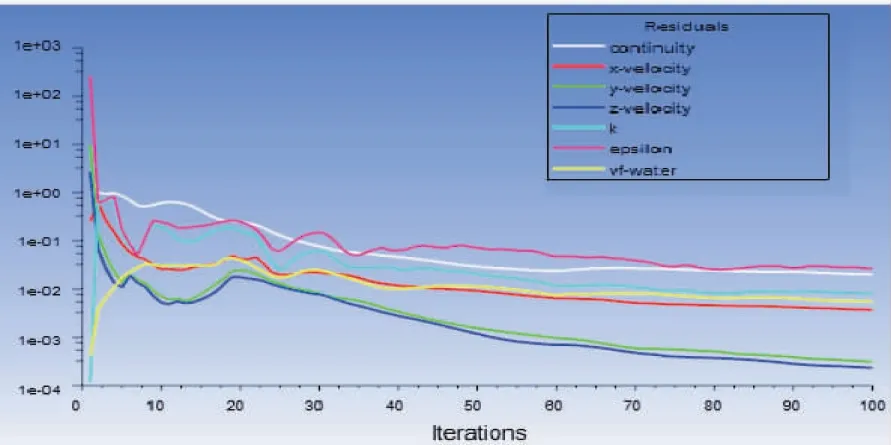
图5 计算收敛图Fig.5 Computing convergence diagram

3 仿真结果

管道的固有频率是其固有属性,与其他因素无关。分析管道在有无流固耦合情况下的固有频率,为辨明管道振型提供理论依据。通过分析3种不同支撑,管道有无流固耦合情况下的前10阶模态,其计算结果如图6所示。

图6 管道有无流固耦合固有频率对比Fig.6 Comparison of natural frequencies of pipes with and withoutfluid-structure interaction

由图6可知,流固耦合下的管道固有频率在3种支撑方式下都小于无流固耦合的。进而可知,流固耦合的存在会降低管道的固有频率,并且随着模态分析阶数的增大,管道固有频率呈现递增趋势。3种支撑方式中,固支-固支支撑的固有频率最大,其次是固支-简支,最后是简支-简支。

为了进一步确定管内积液量和不同支撑方式对管道固有频率的影响。在此基础上,将管内积液量设置为5种体积量,分别为200, 500, 750, 1000, 1500 mL。关于管道的固定方式,分别采用了固支-固支、固支-简支、简支-简支的方式。在入口空气速度为3.98 m/s的情况下,计算5种积液量以及3种不同的支撑方式下的前6阶固有频率。

图7～图9分别是积液量为750 mL时3种支撑方式下的前6阶模态分析。模拟中管道的支撑位置在弯头处,从图中可以发现,管道内变形最大的位置处于支撑位置附近。其中, 1阶和2阶振型中管道变形最严重的位置是水平管段,在3阶和4阶中,变形位置发展到了倾斜管段处,而5阶的振型是倾斜和水平段都发生变形,6阶振型中间水平段的变形减小。

图8 积液量为750 mL,固支-简支支撑方式下前6阶模态分析Fig.8 Liquid accumulation is 750 mL, and first six modal analysis is carried out under fixed support-simple support method

图9 积液量为750 mL,简支-简支支撑方式下前6阶模态分析Fig.9 Liquid accumulation is 750 mL, and first six modal analysis under simple support-simple support method

不同积液量下前6阶固有频率在不同支撑方式下的计算结果如表2(固支-固支)、表3(固支-简支)、表4(简支-简支)所示。从表中可以发现,固支-固支支撑方式下的管道固有频率大于其他两种支撑方式。从计算中可以看出,固支-固支支撑方式管道发生共振的可能性最小,进而在管道结构布置时,选择此方式固定管道最优。相对比空管的固有频率,在通入液体后管道固有频率减小。因积液作为管道的附加质量降低了管道的固有频率。从流固耦合角度看,积液量的增大对管道固有频率有降低趋势,因液体与管道之间的相互作用, 使得管道的固有频率减小。故而当管内积液量足够大时,管道的固有频率会降低,进而管道出现共振现象。

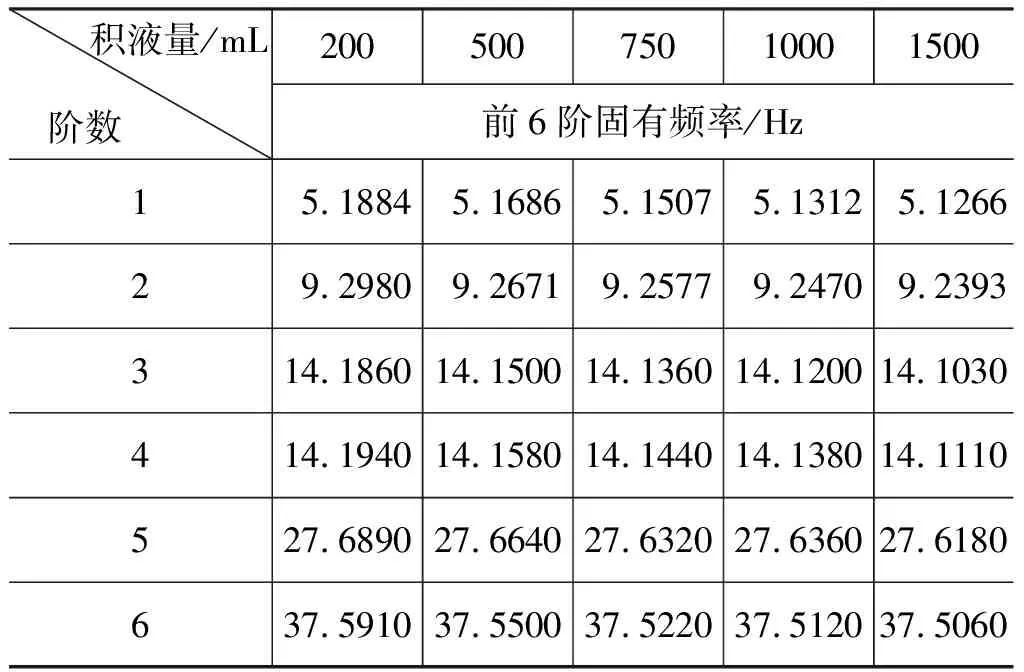
表2 固支-固支下管道的前6阶固有频率Tab.2 First six natural frequencies of pipelines under fixed support-fixed support

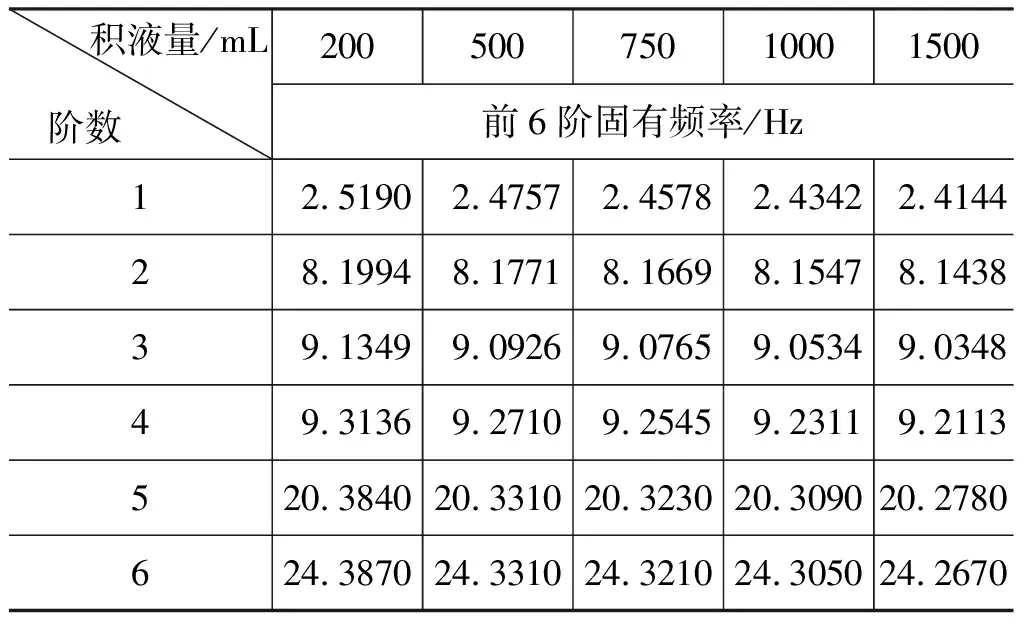
表4 简支-简支下管道的前6阶固有频率Tab.4 First six natural frequencies of pipelines under simple support-simple support

4 结论

(1) 研究表明,流固耦合会降低管道固有频率,且随着模态阶数的增加,管道的固有频率也会增加;

(2) 管道内存在积液时,液体作为附加质量降低了管道的固有频率。随着积液量的增大,固有频率也会降低,因而增大了管道振动;

(3) 相对比固支-简支与简支-简支的支撑方式,固支-固支支撑的固有频率更大一些,因此与管道发生共振的可能性也会降低。