五种方法解决圆中弦的中点轨迹问题

■西北师范大学附属中学 卢会玉

圆中弦的中点轨迹问题是一类常见的题型,多以选择题或填空题的形式出现,下面总结出五种常见的解题方法。 从不同角度分析问题,可以带给同学们不同的解题过程。

题目 由圆x2+y2=9外一点P(5,12)引圆的割线与圆相交于A,B两点,求弦AB的中点M的轨迹方程。

解法一：(直接法)

如图1,设弦AB的中点M的坐标为M(x,y),连接OP,OM,则OM⊥AB。

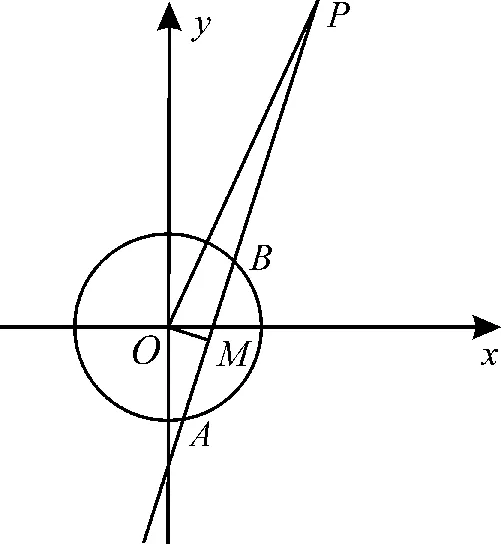
图1

在△OMP中,由两点间的距离公式和勾股定理得:

x2+y2+ (x-5)2+(y-12)2=169。

整理得x2+y2-5x-12y=0,其中-3≤x≤3。

解法二：(定义法)

解法三：(交轨法)

设过点P的割线的斜率为k,则此割线的方程为y-12=k(x-5)。

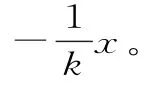
这两条直线的交点就是M,两式联立消去k可得x2+y2-5x-12y=0,其中-3≤x≤3。

解法四：(参数法)

消去参数k可得M点的轨迹方程为x2+y2-5x-12y=0,其中-3≤x≤3。

解法五：(点差法)

以上五种解法都是求轨迹问题的基本方法,有的解法充分利用了圆的条件解题,有的解法突破了圆的局限,适用于一般的过定点P且与二次曲线C交于A,B两点,求AB中点M的轨迹问题,是具有普遍意义的通性通法,有一定的学习价值。