求解椭圆离心率的常见方法

■河南省郑州市第二高级中学 韦道田

椭圆的离心率是椭圆的重要几何性质之一,下面就求解椭圆的离心率(或取值范围)给出几种重要方法,供同学们参考。

一、利用椭圆离心率的定义求解

解析：(1)如图1,切线互相垂直,又半径OA⊥PA,所以△OAP是等腰直角三角形。因为2c=2,即c=1,所以

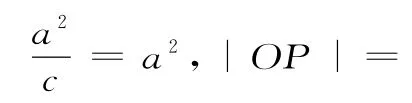
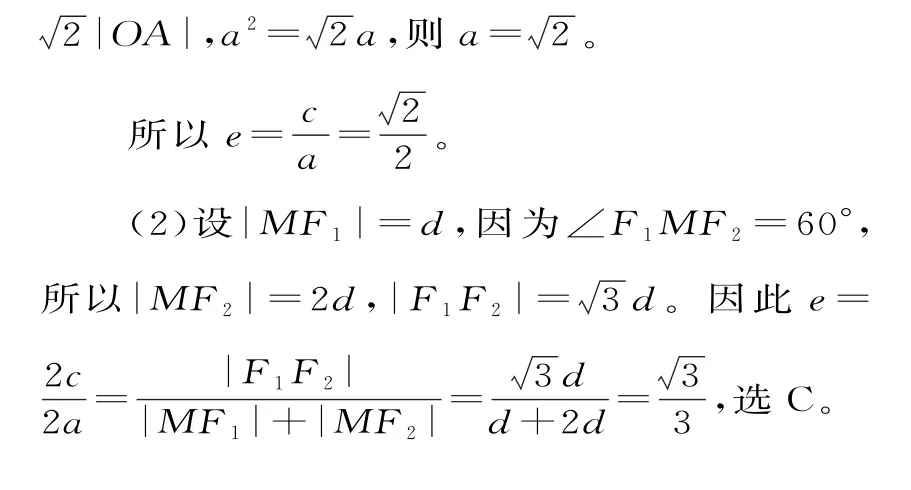
二、利用圆锥曲线的统一定义求解

点评:利用圆锥曲线的统一定义,可以较快地求出圆锥曲线的离心率。

三、构造离心率的方程(不等式)求解

点评:如果直接求解椭圆离心率的值(或取值范围)有困难,那么可以通过构造离心率的方程(或不等式)求解。

四、利用数形结合思想求解

例4【第12届“希望杯”试题】设F1、F2是椭圆的两个焦点,若椭圆上存在点P,使∠F1PF2=120°,则椭圆离心率e的取值范围是_____。

解析：如图2,

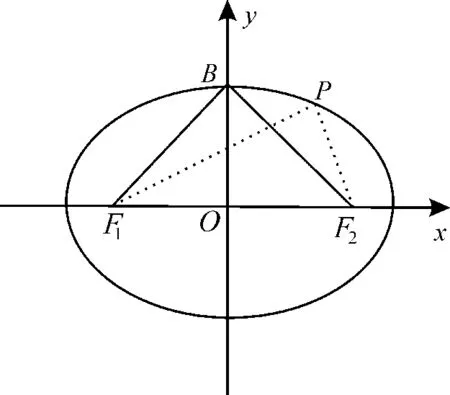
图2

当点P与短轴端点B重合时,∠F1PF2最 大。 于 是 得∠F1PF2≥120°,故tan∠F1PO≥tan 60°

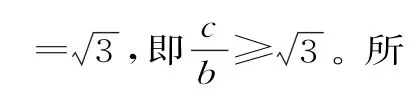
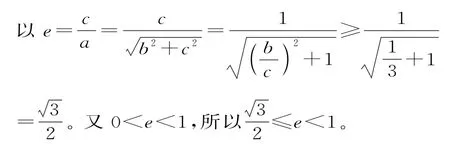
点评:利用数形结合思想求椭圆的离心率e,可回避繁杂的推理与计算过程。

五、利用椭圆的光学性质求解

例5【第一届“希望杯”高二试题】椭圆的两个焦点是F1(3,-6),F2(6,3),一条切线方程为4x=3y,这个椭圆的离心率是_____。

解析：设切点为P,切线为l,作F1、F2关于l的对称点F1'、F2',则由椭圆的光学性质知点P是等腰梯形F1F2F2'F1'对角线的交点,对角线的长应等于椭圆长轴的长。

由点到直线的距离公式,得F1、F2到直线l的距离分别为6、3,可见梯形上、下底长分别为6、12。 该等腰梯形的腰长即椭圆的焦距