例析以“阿波罗尼斯圆”为背景的热点考向

■山东省枣庄市第二中学 付峰峰

一、求最值

二、求参数的范围

例2(2021 年江西省景德镇一中高二期中卷)已知点A(-4,0),B(-1,0),

三、求定值

分析：先根据圆的切线的性质和三角形相似,得到|PO1|=2|PO|,求得点P的轨迹方程,再根据直线与圆相切,利用圆心到直线的距离等于半径,即可求解。

解：由题意得O(0,0),O1(-4,0),不妨设P(x,y),如图1所示。

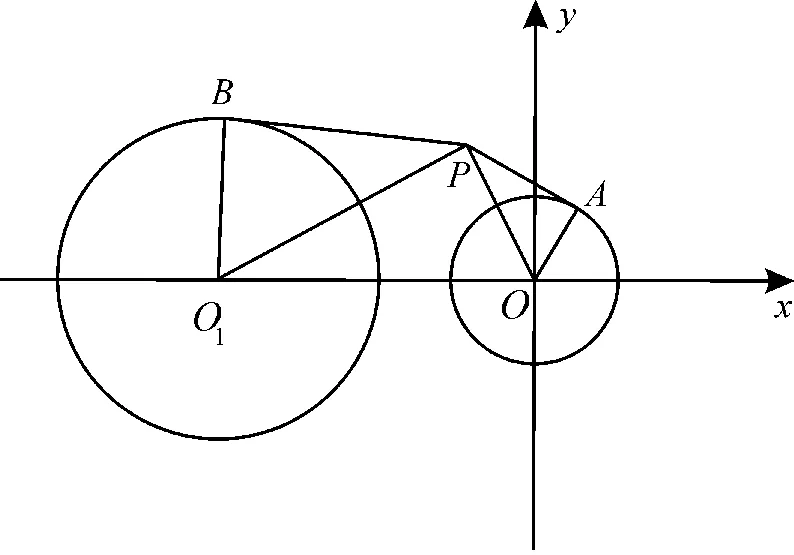
图1

点评:本题主要考查了圆的切线的性质,以及直线与圆的位置关系的应用,解答时先根据圆的切线的性质和三角形相似求得点P的轨迹方程,再根据直线与圆相切列出方程是解答的关键,着重考查了同学们的推理与运算能力,属于中档题。

跟踪练习：

3.在平面直角坐标系xOy中,M,N是两定点,点P是圆O:x2+y2=1 上任意一点,满足|PM|=2|PN|,求|MN|的长。

解析：由于M,N是两定点,不妨假设M,N在x轴上,如图2所示。设M(m,0),N(n,0),P(x,y),|PM|=2|PN|,即|PM|2=4|PN|2。

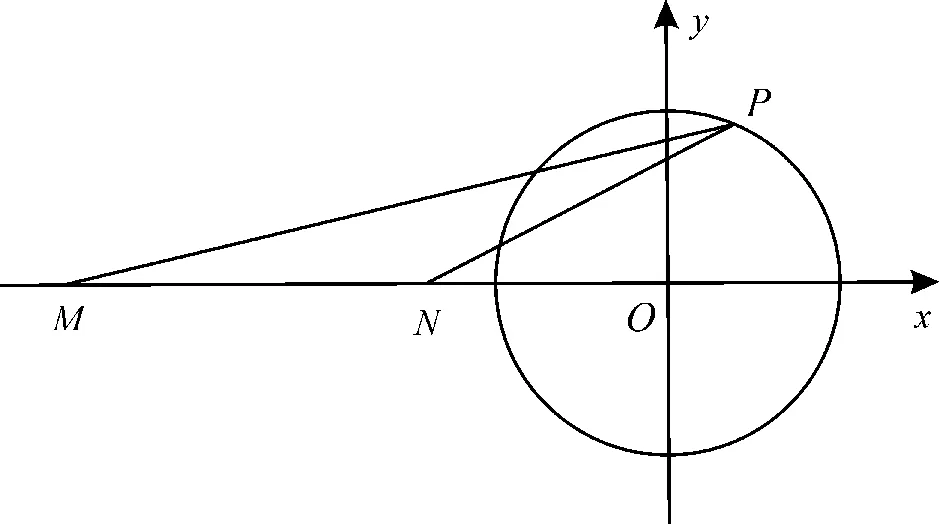
图2

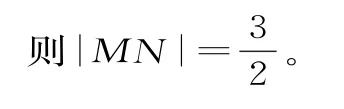
四、求轨迹

五、逆用阿波罗尼斯圆

例5唐代诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河。”诗中隐含着一个有趣的数学问题——“将军饮马”,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回军营,怎样走才能使总路程最短? 在平面直角坐标系